8 神经网络及Python实现
1 人工神经网络的历史
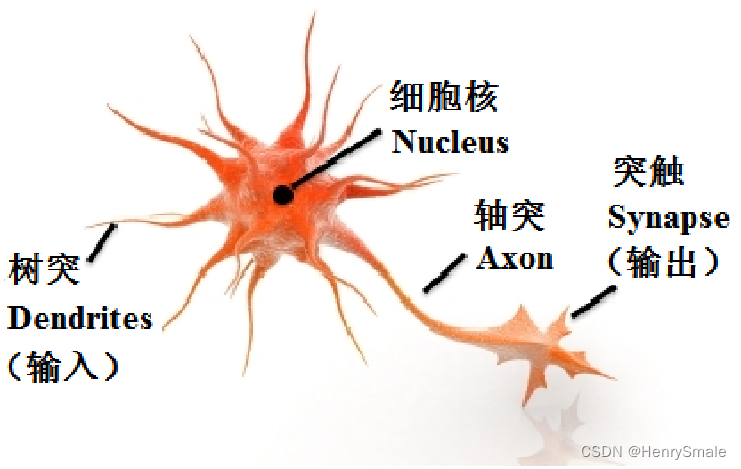
1.1 生物模型
1943年,心理学家W.S.McCulloch和数理逻辑学家W.Pitts基于神经元的生理特征,建立了单个神经元的数学模型(MP模型)。
1.2 数学模型
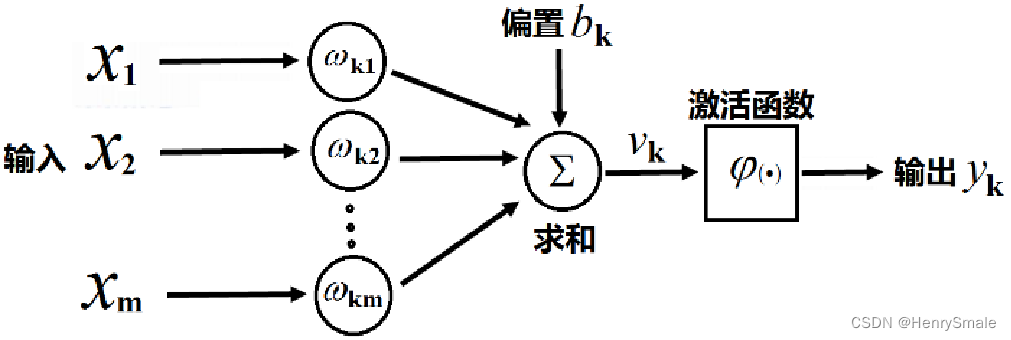
yk=φ(∑i=1mωkixi+bk)=φ(WkTX+b)y_{k}=\varphi\left(\sum_{i=1}^{m} \omega_{k i} x_{i}+b_{k}\right)=\varphi\left(W_{k}^{T} X+b\right) yk=φ(i=1∑mωkixi+bk)=φ(WkTX+b)
1.3 感知器
1957年,Frank Rosenblatt从纯数学的度重新考察这一模型,指出能够从一些输入输出对(X,y)(X, y)(X,y)中通过学习算法获得权重 WWW和bbb 。
问题:给定一些输入输出对(X,y)(X, y)(X,y),其中y=±1y = \pm 1y=±1,求一个函数,使 f(X)=yf(X) = yf(X)=y。
感知器算法:设定f(X)=sign(WTX+b)f(X) = sign (W^T X + b)f(X)=sign(WTX+b),从一堆输入输出中自动学习,获得WWW和bbb。
感知器算法(Perceptron Algorithm):
(1)随机选择WWW和bbb;
(2)取一个训练样本 (X,y)(X, y)(X,y)
(i) 若 WTX+b>0W^T X + b > 0WTX+b>0且y=−1y = -1y=−1,则:
W=W−X,b=b−1.W = W - X, b = b - 1.W=W−X,b=b−1.
(ii)若 WTX+b<0W^T X + b < 0WTX+b<0且y=+1y = +1y=+1,则:
W=W+X,b=b+1.W = W + X, b = b + 1.W=W+X,b=b+1.
(3)再取另一个(X,y)(X, y)(X,y),回到(2);
(4)终止条件:直到所有输入输出对(X,y)(X, y)(X,y)都不满足(2)中(i)和(ii)之一,退出循环。
感知器算法演示:
1.4 多层网络
两层神经网络例子:
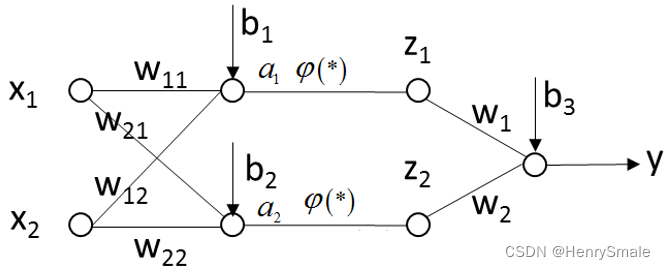
a1=ω11x1+ω12x2+b1a2=ω21x1+ω22x2+b2z1=φ(a1)z2=φ(a2)y=ω1z1+ω2z2+b3\begin{array}{l} a_{1}=\omega_{11} x_{1}+\omega_{12} x_{2}+b_{1} \\ a_{2}=\omega_{21} x_{1}+\omega_{22} x_{2}+b_{2} \\ z_{1}=\varphi\left(a_{1}\right) \\ z_{2}=\varphi\left(a_{2}\right) \\ y=\omega_{1} z_{1}+\omega_{2} z_{2}+b_{3} \end{array} a1=ω11x1+ω12x2+b1a2=ω21x1+ω22x2+b2z1=φ(a1)z2=φ(a2)y=ω1z1+ω2z2+b3
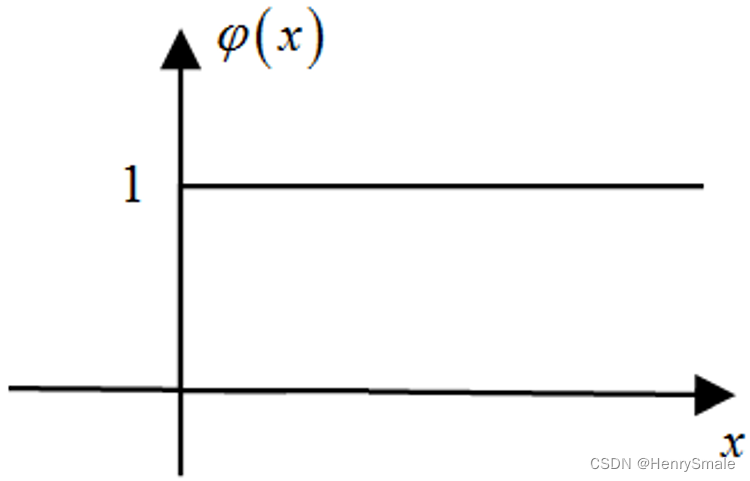
其中,φ(⋅)\varphi(\cdot)φ(⋅)为非线性函数。
定理:当 φ(x)\varphi(x)φ(x)为阶跃函数时,三层网络可以模拟任意决策面。
举例:
- 两层神经网络模拟一个非线性决策面,最后W取[1,1,1], b取-2.5;
- 如果决策面是四边形,第二层神经元就有4个,最后W取[1,1,1,1], b取-3.5;
- 如果决策面是圆的话,第二层就有无穷多个神经元,去逼近圆;
- 如果决策面分开了,要在第二层里把神经元竖着写下去,并且加一层神经元,把他们的结果合并起来。对于两个三角形的情况,最后W取[1,1], b取-0.5。只要有一个1,最后结果就是1;都是0,最后结果就是0。
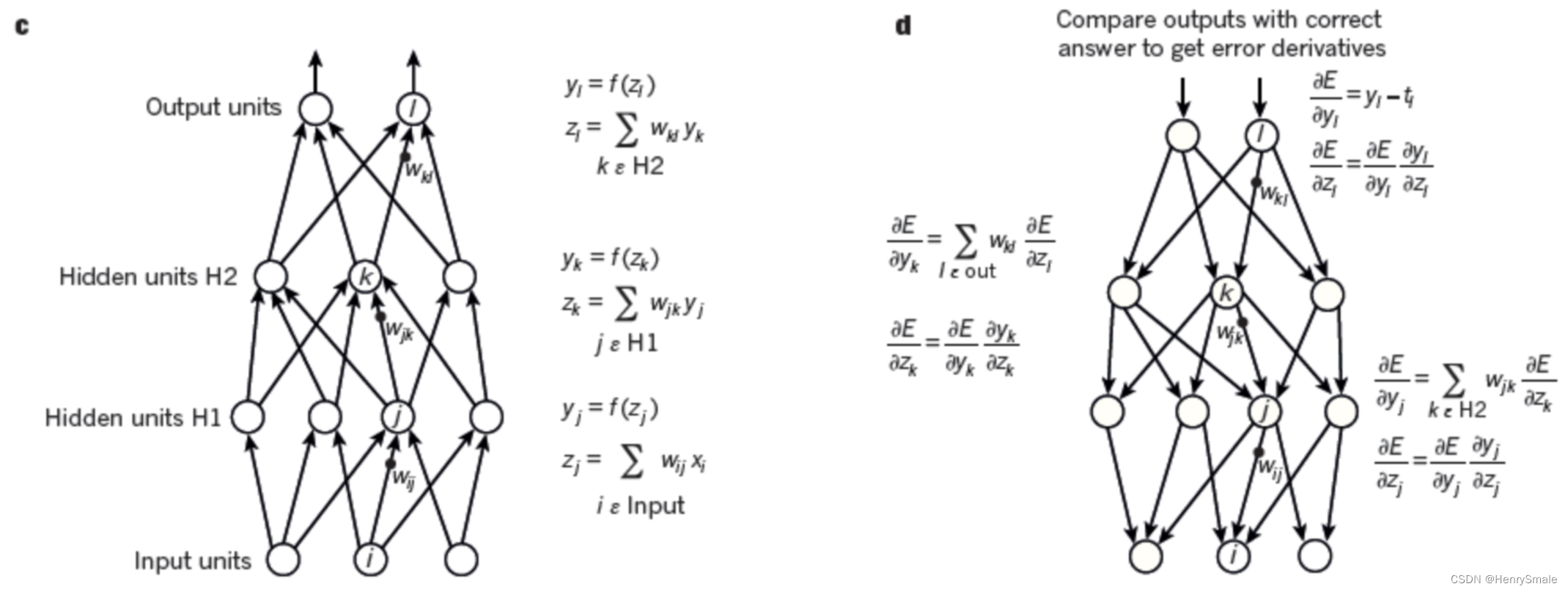
学习算法:后向传播(Back Propogation Algorithm)。
输入(X,Y)(X, Y)(X,Y),其中X=[x1,x2]TX = [x_1,x_2]^TX=[x1,x2]T, YYY是标签值(label),即我们希望改变ω\omegaω和bbb,使得标签值YYY与网络输出的预测值yyy尽量接近。
定义目标函数为:
minE(ω,b)=minE(X,Y)[(Y−y)2]\min E(ω,b) = \min E_{(X,Y)}[(Y−y)^2] minE(ω,b)=minE(X,Y)[(Y−y)2]
最简单的梯度下降法(Gradient Descent Method):
ω(new )=ω(old)−α∂E∂ω∣ω(old),b(old)b(new )=b(old)−α∂E∂b∣ω(old),b(old)\begin{array}{l} \omega^{(\text {new })}=\omega^{(o l d)}-\left.\alpha \frac{\partial E}{\partial \omega}\right|_{\omega^{(o l d)}, b^{(o l d)}} \\ b^{(\text {new })}=b^{(o l d)}-\left.\alpha \frac{\partial E}{\partial b}\right|_{\omega^{(o l d)}, b^{(o l d)}} \end{array} ω(new )=ω(old)−α∂ω∂Eω(old),b(old)b(new )=b(old)−α∂b∂Eω(old),b(old)
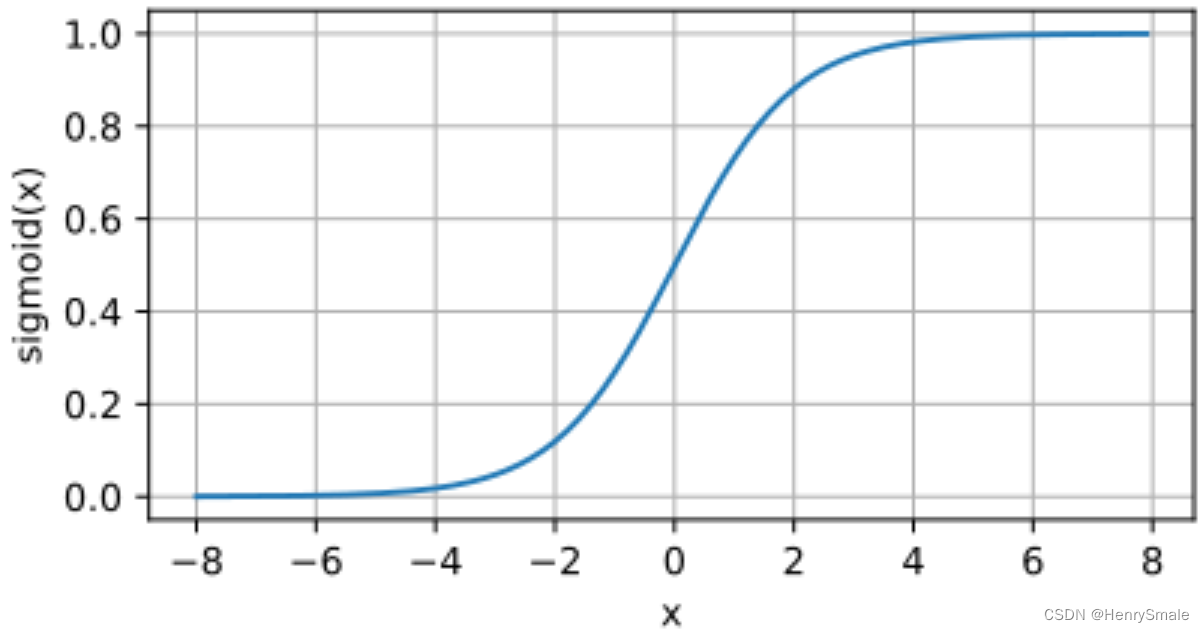
常见非线性函数φ(x)\varphi(x)φ(x)的选择:
(1)Sigmoid:φ(x)=11+e−x,φ′(x)=φ(x)[1−φ(x)]\varphi(x) = \frac{1}{1+ e^{-x}}, \varphi'(x) = \varphi(x)[1 - \varphi(x)]φ(x)=1+e−x1,φ′(x)=φ(x)[1−φ(x)]
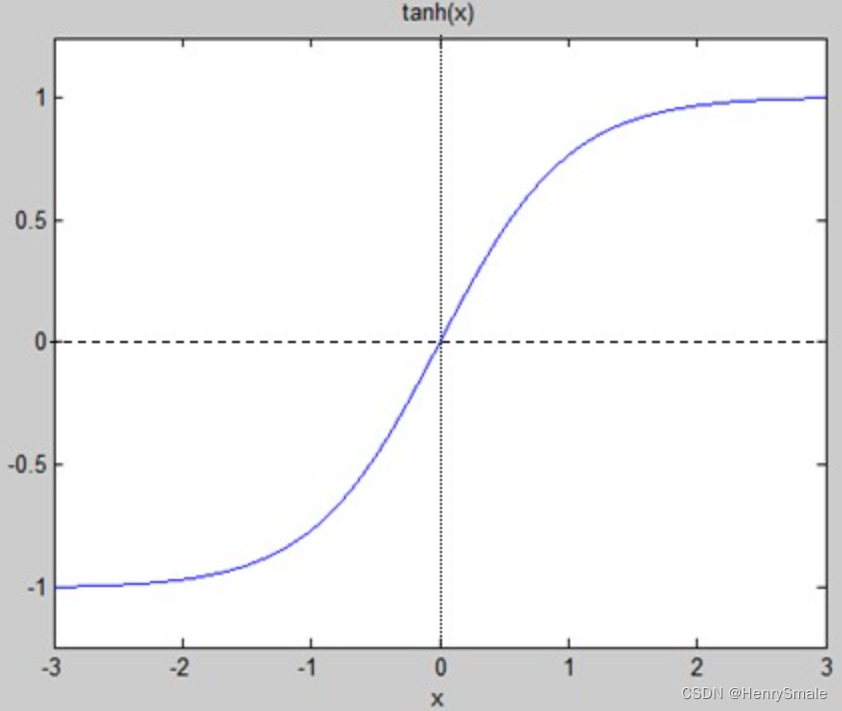
(2)tanh:φ(x)=ex−e−xex+e−x,φ′(x)=1−[φ(x)]2\varphi(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}, \varphi'(x) = 1 - [\varphi(x)]^2φ(x)=ex+e−xex−e−x,φ′(x)=1−[φ(x)]2
多层神经网络的优势: - (1)基本单元简单,多个基本单元可扩展为非常复杂的非线性函数。因此易于构建,同时模型有很强的表达能力;
- (2)训练和测试的计算并行性非常好,有利于在分布式系统上的应用;
- (3)模型构建来源于对人脑的仿生,话题丰富,各种领域的研究人员都有兴趣,都能做贡献。
多层神经网络的劣势:
- (1)数学不漂亮,优化算法只能获得局部极值,算法性能与初始值有关;
- (2)不可解释。训练神经网络获得的参数与实际任务的关联性非常模糊;
- (3)模型可调整的参数很多 (网络层数、每层神经元个数、非线性函数、学习率、优化方法、终止条件等等),使得训练神经网络变成了一门“艺术”;
- (4)如果要训练相对复杂的网络,需要大量的训练样本。
训练建议:
- (1)一般情况下,在训练集上的目标函数的平均值(cost)会随着训练的深入而不断减小,如果这个指标有增大情况,停下来。有两种情况:第一是采用的模型不够复杂,以致于不能在训练集上完全拟合;第二是已经训练很好了;
- (2)分出一些验证集(Validation Set),训练的本质目标是在验证集上获取最大的识别率。因此训练一段时间后,必须在验证集上测试识别率,保存使验证集上识别率最大的模型参数,作为最后结果;
- (3)注意调整学习率(Learning Rate),如果刚训练几步cost就增加,一般来说是学习率太高了;如果每次cost变化很小,说明学习率太低。
2 参数设置
2.1 随机梯度下降
(1)不用每输入一个样本就去变换参数,而是输入一批样本(叫做一个BATCH或MINI-BATCH),求出这些样本的梯度平均值后,根据这个平均值改变参数。
(2)在神经网络训练中,BATCH的样本数大致设置为50-200不等。
batch_size = option.batch_size;
m = size(train_x,1);
num_batches = m / batch_size;
for k = 1 : iterationkk = randperm(m);for l = 1 : num_batchesbatch_x = train_x(kk((l - 1) * batch_size + 1 : l * batch_size), :);batch_y = train_y(kk((l - 1) * batch_size + 1 : l * batch_size), :);nn = nn_forward(nn,batch_x,batch_y);nn = nn_backpropagation(nn,batch_y);nn = nn_applygradient(nn);end
end
m = size(batch_x,2);
前向计算
nn.cost(s) = 0.5 / m * sum(sum((nn.a{k} - batch_y).^2)) + 0.5 * nn.weight_decay * cost2;
后向传播
nn.W_grad{nn.depth-1} = nn.theta{nn.depth}*nn.a{nn.depth-1}'/m + nn.weight_decay*nn.W{nn.depth-1};
nn.b_grad{nn.depth-1} = sum(nn.theta{nn.depth},2)/m;
2.2 激活函数选择

2.3 训练数据初始化
建议:做均值和方差归一化
newX=X−mean(X)std(X)newX = \frac{X - mean(X)}{std(X)} newX=std(X)X−mean(X)
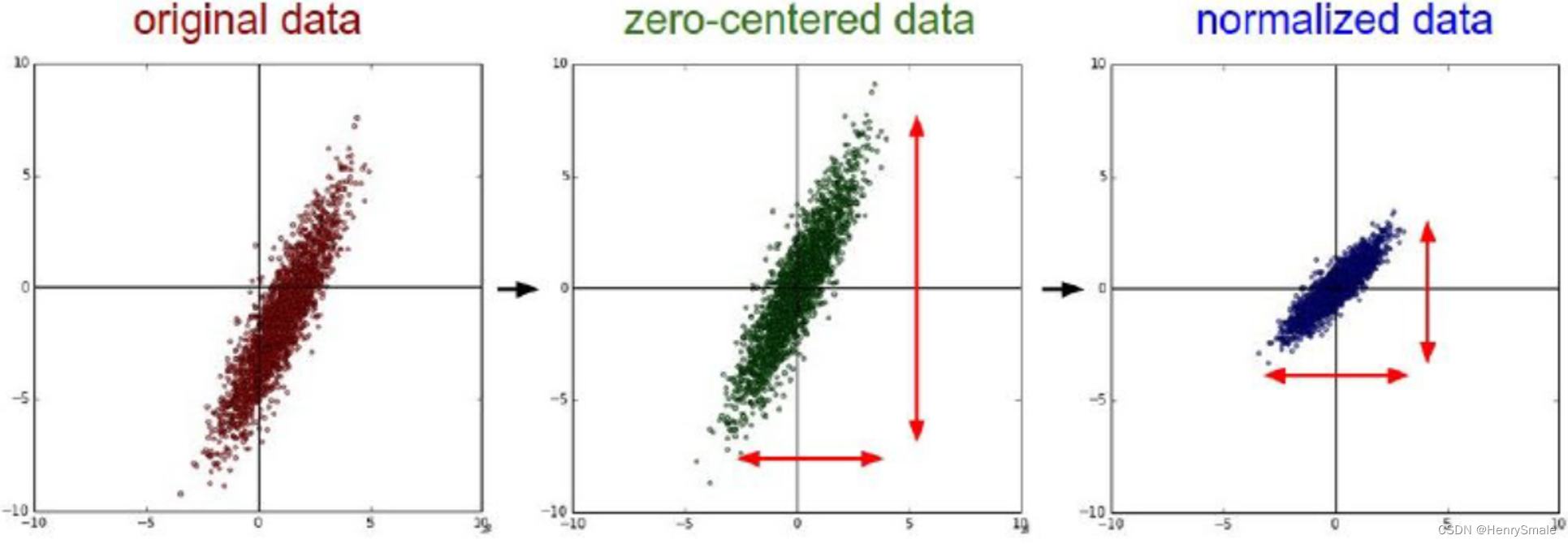
[U,V] = size(xTraining);
avgX = mean(xTraining);
sigma = std(xTraining);
xTraining = (xTraining - repmat(avgX,U,1))./repmat(sigma,U,1);
2.4 (ω,b)(\omega,b)(ω,b)的初始化
梯度消失现象:如果WXT+bW X^T + bWXT+b一开始很大或很小,那么梯度将趋近于0,反向传播后前面与之相关的梯度也趋近于0,导致训练缓慢。
因此,我们要使WXT+bW X^T + bWXT+b一开始在零附近。
一种比较简单有效的方法是:
- (W,b)(W,b)(W,b)初始化从区间(−1d,1d)(- \frac{1}{\sqrt{d}}, \frac{1}{\sqrt{d}})(−d1,d1)均匀随机取值。其中ddd为(W,b)(W,b)(W,b)所在层的神经元个数。
- 可以证明,如果XXX服从正态分布,均值0,方差1,且各个维度无关,而(W,b)(W,b)(W,b)是 (−1d,1d)(- \frac{1}{\sqrt{d}}, \frac{1}{\sqrt{d}})(−d1,d1)的均匀分布,则 WXT+bW X^T + bWXT+b是均值为0, 方差为1/3的正态分布。
nn.W{k} = 2*rand(height, width)/sqrt(width)-1/sqrt(width);
nn.b{k} = 2*rand(height, 1)/sqrt(width)-1/sqrt(width);
参数初始化是一个热点领域,相关论文包括:

2.5 Batch normalization
论文:Batch normalization accelerating deep network training by reducing internal covariate shift (2015)
基本思想:既然我们希望每一层获得的值都在0附近,从而避免梯度消失现象,那么我们为什么不直接把每一层的值做基于均值和方差的归一化呢?
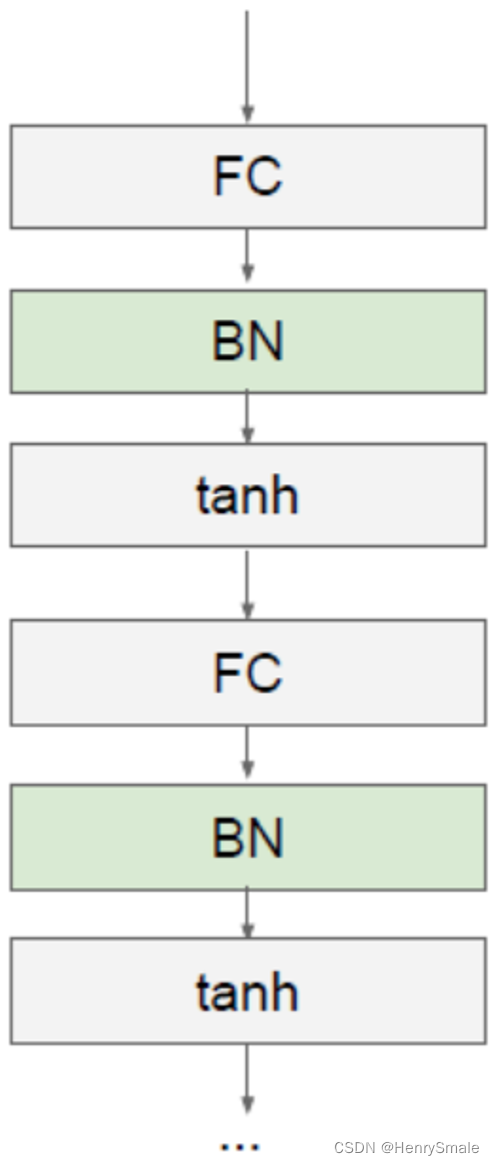
每一层FC(Fully Connected Layer)接一个BN(Batch Normalization)层。
x^(k)=x(k)−E[x(k)]Var[x(k)]\hat{x}^{(k)} = \frac{x^{(k)} - E[x^{(k)}]}{\sqrt{\mathbf{Var}[x^{(k)}]}} x^(k)=Var[x(k)]x(k)−E[x(k)]
算法流程:

前向计算:
y = nn.W{k-1} * nn.a{k-1} + repmat(nn.b{k-1},1,m);
if nn.batch_normalizationnn.E{k-1} = nn.E{k-1}*nn.vecNum + sum(y,2);nn.S{k-1} = nn.S{k-1}.^2*(nn.vecNum-1) + (m-1)*std(y,0,2).^2;nn.vecNum = nn.vecNum + m;nn.E{k-1} = nn.E{k-1}/nn.vecNum;nn.S{k-1} = sqrt(nn.S{k-1}/(nn.vecNum-1));y = (y - repmat(nn.E{k-1},1,m))./repmat(nn.S{k-1}+0.0001*ones(size(nn.S{k-1})),1,m);y = nn.Gamma{k-1}*y+nn.Beta{k-1};
end;
switch nn.activaton_functioncase 'sigmoid'nn.a{k} = sigmoid(y);case 'tanh'nn.a{k} = tanh(y);
后向传播:
nn.theta{k} = ((nn.W{k}'*nn.theta{k+1})) .* nn.a{k} .* (1 - nn.a{k});
if nn.batch_normalizationx = nn.W{k-1} * nn.a{k-1} + repmat(nn.b{k-1},1,m);x = (x - repmat(nn.E{k-1},1,m))./repmat(nn.S{k- 1}+0.0001*ones(size(nn.S{k-1})),1,m);temp = nn.theta{k}.*x;nn.Gamma_grad{k-1} = sum(mean(temp,2));nn.Beta_grad{k-1} = sum(mean(nn.theta{k},2));nn.theta{k} = nn.Gamma{k-1}*nn.theta{k}./repmat((nn.S{k-1}+0.0001),1,m);
end;
nn.W_grad{k-1} = nn.theta{k}*nn.a{k-1}'/m + nn.weight_decay*nn.W{k-1};
nn.b_grad{k-1} = sum(nn.theta{k},2)/m;
2.6 目标函数选择
- 正则项 (Regulation Term)
L(W)=F(W)+R(W)=12(∑1batch_size∣∣yi−Yi∣∣2+β∑k∑lWk,l2)\begin{array}{l} L(W)&=F(W)+R(W) \\ & = \frac{1}{2}\left(\sum_1^{batch\_size} ||y_i -Y_i||^2 + \beta\sum_k \sum_l W_{k,l}^2 \right) \end{array} L(W)=F(W)+R(W)=21(∑1batch_size∣∣yi−Yi∣∣2+β∑k∑lWk,l2)
前向计算
cost2 = cost2 + sum(sum(nn.W{k-1}.^2));
nn.cost(s) = 0.5 / m * sum(sum((nn.a{k} - batch_y).^2)) + 0.5 * nn.weight_decay * cost2;
后向传播
nn.W_grad{k-1} = nn.theta{k}*nn.a{k-1}'/m + nn.weight_decay*nn.W{k-1};
- 如果是分类问题,F(W)F(W)F(W)可以采用SOFTMAX函数和交叉熵的组合。
(a)SOFTMAX函数:

pi=eyi∑j=1Neyjp_i = \frac{e^{y_i}}{\sum_{j=1}^{N} e^{y_j}} pi=∑j=1Neyjeyi
通过网络学习Y=[y1,y2,…,yN]TY = [y_1, y_2, \dots, y_N]^TY=[y1,y2,…,yN]T到P=[p1,p2,…,pN]TP = [p_1, p_2, \dots, p_N]^TP=[p1,p2,…,pN]T的映射,其中∑i=1Npi=1\sum_{i=1}^N p_i = 1∑i=1Npi=1。
(b)交叉熵
目标函数为:
E=−∑i=1Nci∗log(pi)E = - \sum_{i=1}^N c_i * \log(p_i) E=−i=1∑Nci∗log(pi)
(c)SOFTMAX函数和交叉熵的组合
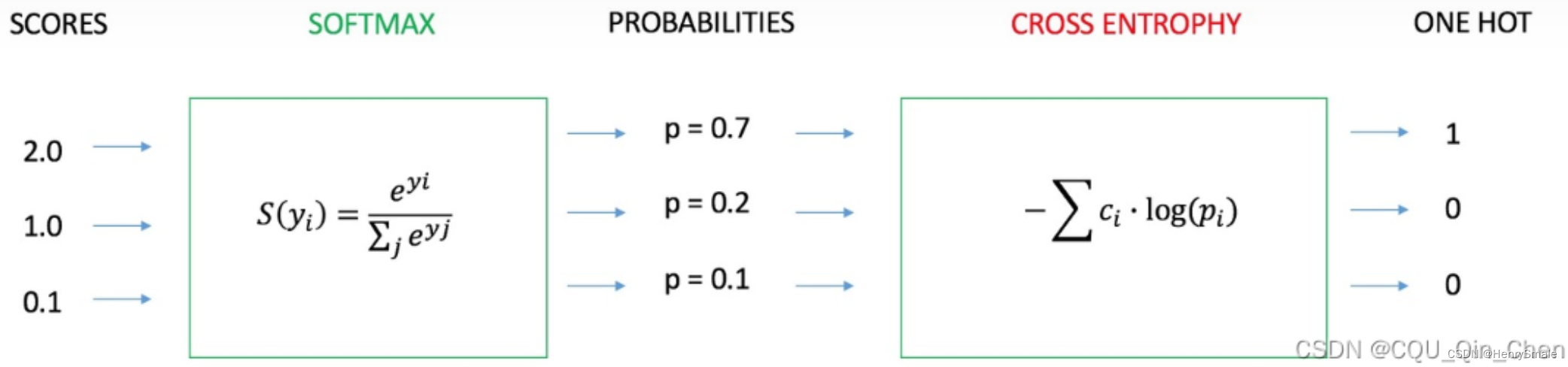
如果F(W)F(W)F(W)是SOFTMAX函数和交叉熵的组合,那么求导将会有非常简单的形式:
∂E∂yi=pi−ci\frac{\partial E}{\partial y_i} = p_i - c_i ∂yi∂E=pi−ci
前向计算
if strcmp(nn.objective_function,'Cross Entropy')nn.cost(s) = -0.5*sum(sum(batch_y.*log(nn.a{k})))/m + 0.5 * nn.weight_decay * cost2;
后向传播
case 'softmax'y = nn.W{nn.depth-1} * nn.a{nn.depth-1} + repmat(nn.b{nn.depth-1},1,m);nn.theta{nn.depth} = nn.a{nn.depth} - batch_y;
2.7 参数更新策略
(1)常规的更新 (Vanilla Stochastic Gradient Descent)
nn.W{k} = nn.W{k} - nn.learning_rate*nn.W_grad{k};
nn.b{k} = nn.b{k} - nn.learning_rate*nn.b_grad{k};
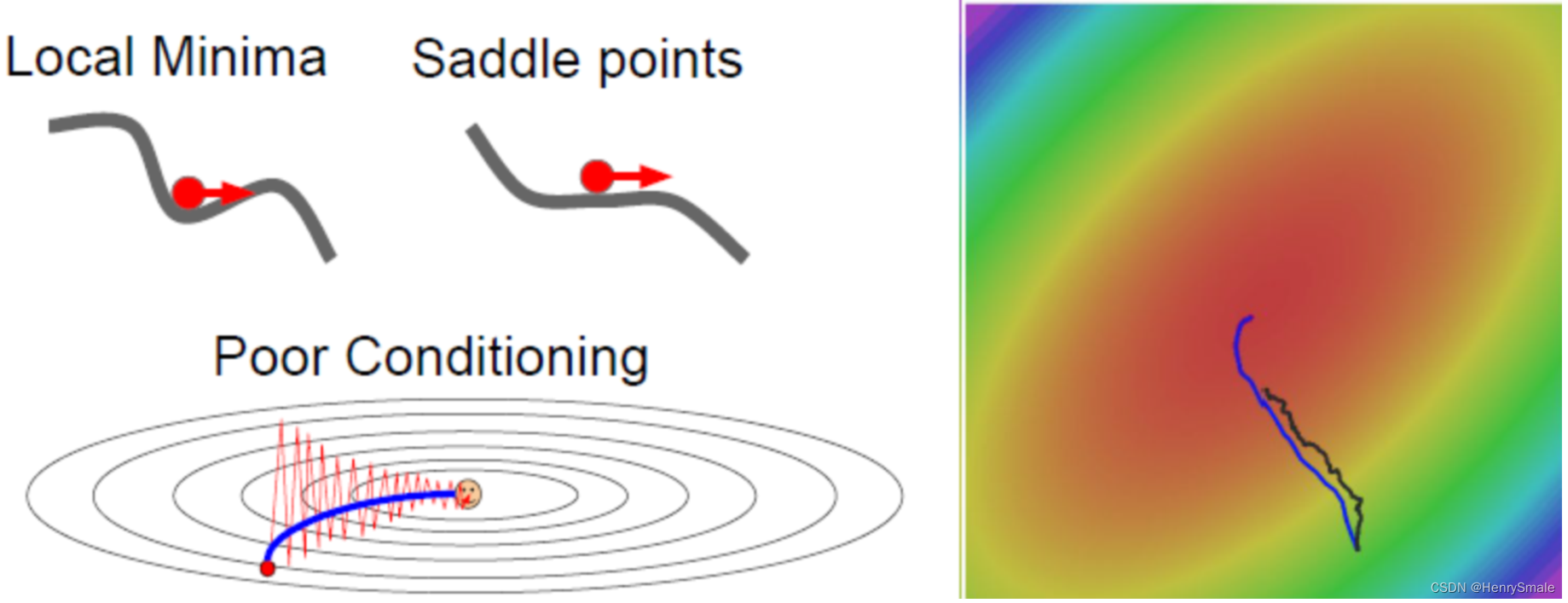
SGD的问题
(1)(W,b)(W,b)(W,b)的每一个分量获得的梯度绝对值有大有小,一些情况下,将会迫使优化路径变成Z字形状。
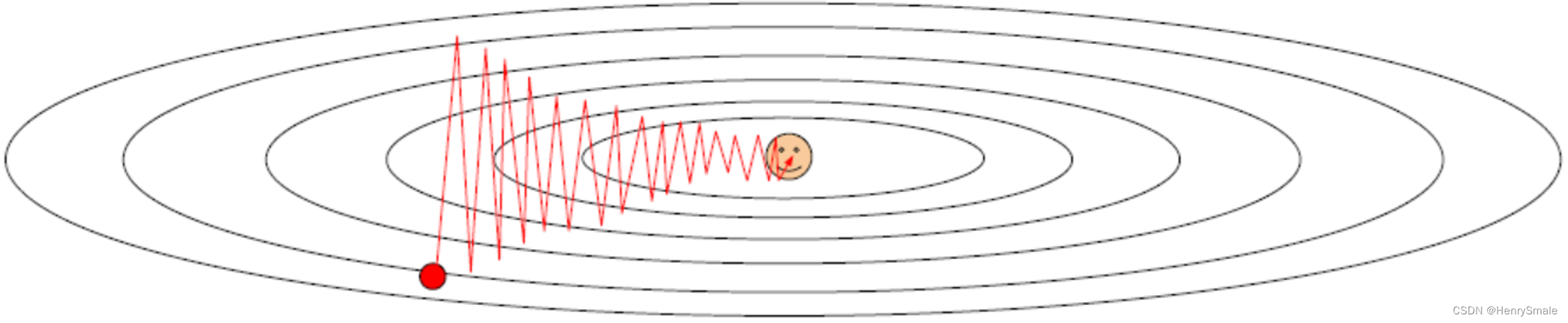
(2)SGD求梯度的策略过于随机,由于上一次和下一次用的是完全不同的BATCH数据,将会出现优化的方向随机的情况。
L(W)=1N∑i=1NLi(xi,yi,W)∇L(W)=1N∑i=1N∇WLi(xi,yi,W)\begin{array}{l} L(W) = \frac{1}{N} \sum_{i = 1}^N L_i(x_i, y_i, W) \\ \nabla L(W) = \frac{1}{N} \sum_{i = 1}^N \nabla_W L_i(x_i, y_i, W) \end{array} L(W)=N1∑i=1NLi(xi,yi,W)∇L(W)=N1∑i=1N∇WLi(xi,yi,W)
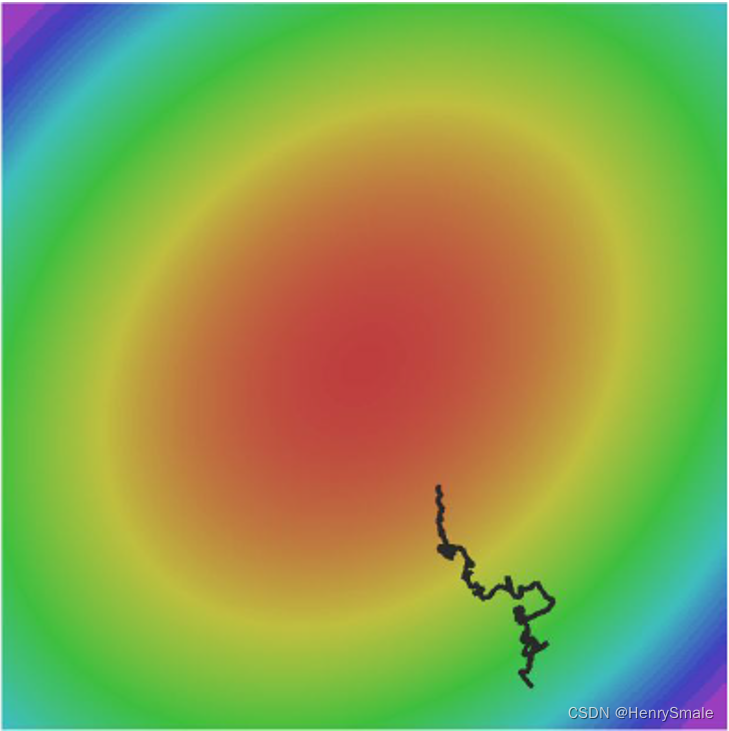
解决各个方向梯度不一致的方法:
(1)AdaGrad
AdaGrad 算法在随机梯度下降法的基础上,通过记录各个分量梯度的累计情况, 以对不同的分量方向的步长做出调整。具体而言,利用 Gk=∑i=1kgi⊙giG^k=\sum^k_{i=1} g_i⊙g_iGk=∑i=1kgi⊙gi 记录分量梯度的累计,并构造如下迭代格式:
xk+1=xk−αGk+ϵ1n⊙gk,Gk+1=Gk+gk+1⊙gk+1.x^{k+1} =x^k−\frac{α}{G^k+ϵ\mathbf{1}_n}⊙g^k, \\ G^{k+1} = G^k+g^{k+1}⊙g^{k+1}. xk+1=xk−Gk+ϵ1nα⊙gk,Gk+1=Gk+gk+1⊙gk+1.

if strcmp(nn.optimization_method, 'AdaGrad')nn.rW{k} = nn.rW{k} + nn.W_grad{k}.^2;
nn.rb{k} = nn.rb{k} + nn.b_grad{k}.^2;nn.W{k} = nn.W{k} - nn.learning_rate*nn.W_grad{k}./(sqrt(nn.rW{k})+0.001);nn.b{k} = nn.b{k} - nn.learning_rate*nn.b_grad{k}./(sqrt(nn.rb{k})+0.001);
(2)RMSProp

if strcmp(nn.optimization_method, 'RMSProp')
nn.rW{k} = 0.9*nn.rW{k} + 0.1*nn.W_grad{k}.^2;
nn.rb{k} = 0.9*nn.rb{k} + 0.1*nn.b_grad{k}.^2;nn.W{k} = nn.W{k} - nn.learning_rate*nn.W_grad{k}./(sqrt(nn.rW{k})+0.001);nn.b{k} = nn.b{k} - nn.learning_rate*nn.b_grad{k}./(sqrt(nn.rb{k})+0.001); %rho = 0.9
解决梯度随机性问题:
(3)Momentum
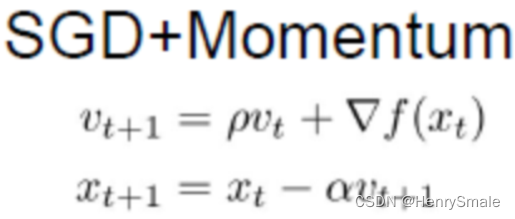
if strcmp(nn.optimization_method, 'Momentum')
nn.vW{k} = 0.5*nn.vW{k} + nn.learning_rate*nn.W_grad{k};nn.vb{k} = 0.5*nn.vb{k} + nn.learning_rate*nn.b_grad{k};nn.W{k} = nn.W{k} - nn.vW{k};
nn.b{k} = nn.b{k} - nn.vb{k}; %rho = 0.5;
同时两个问题:
(4)Adam

if strcmp(nn.optimization_method, 'Adam')
nn.sW{k} = 0.9*nn.sW{k} + 0.1*nn.W_grad{k};
nn.sb{k} = 0.9*nn.sb{k} + 0.1*nn.b_grad{k};
nn.rW{k} = 0.999*nn.rW{k} + 0.001*nn.W_grad{k}.^2;
nn.rb{k} = 0.999*nn.rb{k} + 0.001*nn.b_grad{k}.^2;nn.W{k} = nn.W{k} - 10*nn.learning_rate*nn.sW{k}./sqrt(1000*nn.rW{k}+0.00001);nn.b{k} = nn.b{k} - 10*nn.learning_rate*nn.sb{k}./sqrt(1000*nn.rb{k}+0.00001); %rho1 = 0.9, rho2 = 0.999, delta = 0.00001
2.8 训练建议
(1) Batch Normalization 比较好用,用了这个后,对学习率、参数更新策略等不敏感。建议如果用Batch Normalization, 更新策略用最简单的SGD即可,我的经验是加上其他反而不好。
(2)如果不用Batch Normalization, 通过合理变换其他参数组合,也可以达到目的。
(3)由于梯度累积效应,AdaGrad, RMSProp, Adam三种更新策略到了训练的后期会很慢,可以采用提高学习率的策略来补偿这一效应。
参考文献
浙江大学胡浩基《机器学习:人工神经网络介绍》
相关文章:

8 神经网络及Python实现
1 人工神经网络的历史 1.1 生物模型 1943年,心理学家W.S.McCulloch和数理逻辑学家W.Pitts基于神经元的生理特征,建立了单个神经元的数学模型(MP模型)。 1.2 数学模型 ykφ(∑i1mωkixibk)φ(WkTXb)y_{k}\varphi\left(\sum_{i1…...
使用QIS(Quantum Image Sensor)图像重建总结(1)
最近看了不少使用QIS重建图像的文章,觉得比较完整详细的还是Abhiram Gnanasambandam的博士论文:https://hammer.purdue.edu/articles/thesis/Computer_vision_at_low_light/20057081 1 介绍 讲述了又墨子的小孔成像原理,到交卷相机…...
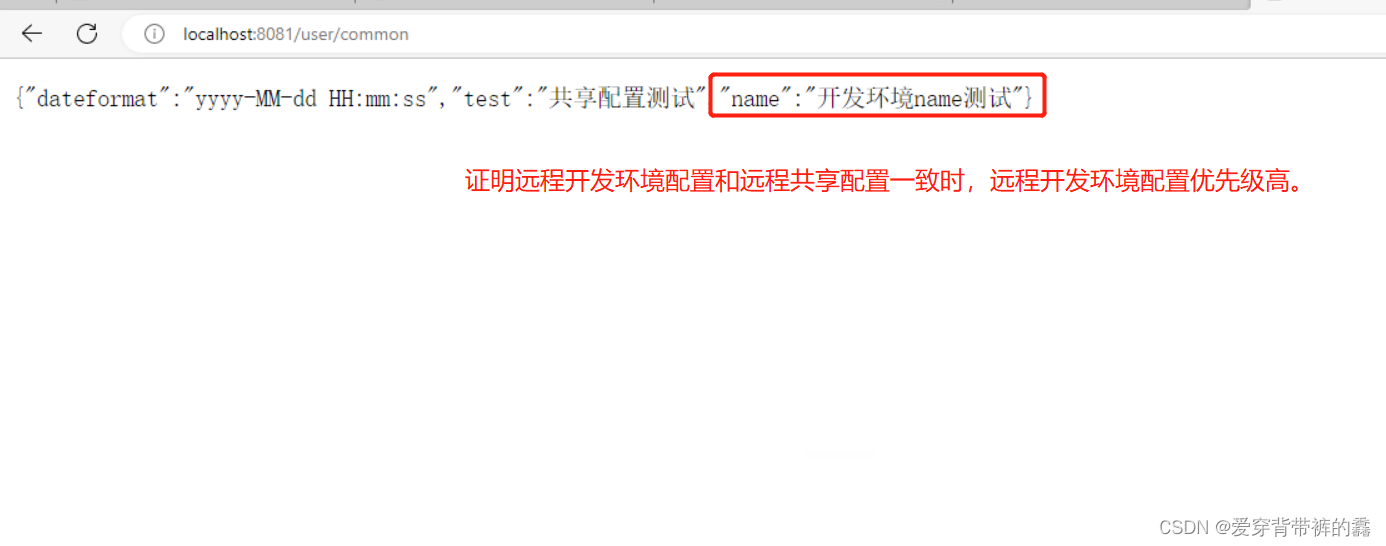
【SpringCloud】SpringCloud教程之Nacos实战(二)
目录前言一.Nacos实现配置管理二.Nacos拉取配置三.Nacos配置热更新(自动刷新,不需要重启服务)1.在有Value注入变量所在类添加注解2.新建类用于属性加载和配置热更新四.Nacos多环境配置共享1.多环境共享配置2.配置的加载优先级测试3.配置优先级前言 Nacos实战一&…...

利用Qemu工具仿真ARM64平台
Windows系统利用Qemu仿真ARM64平台0 写在最前1 Windows安装Qemu1.1 下载Qemu1.2 安装Qemu1.3 添加环境变量1.4测试安装是否成功2. Qemu安装Ubuntu-Server-Arm-642.1 安装前的准备2.2 安装Ubuntu server arm 64位镜像3 Windows配置Qemu网络和传输文件3.1 参考内容3.2 Windows安装…...
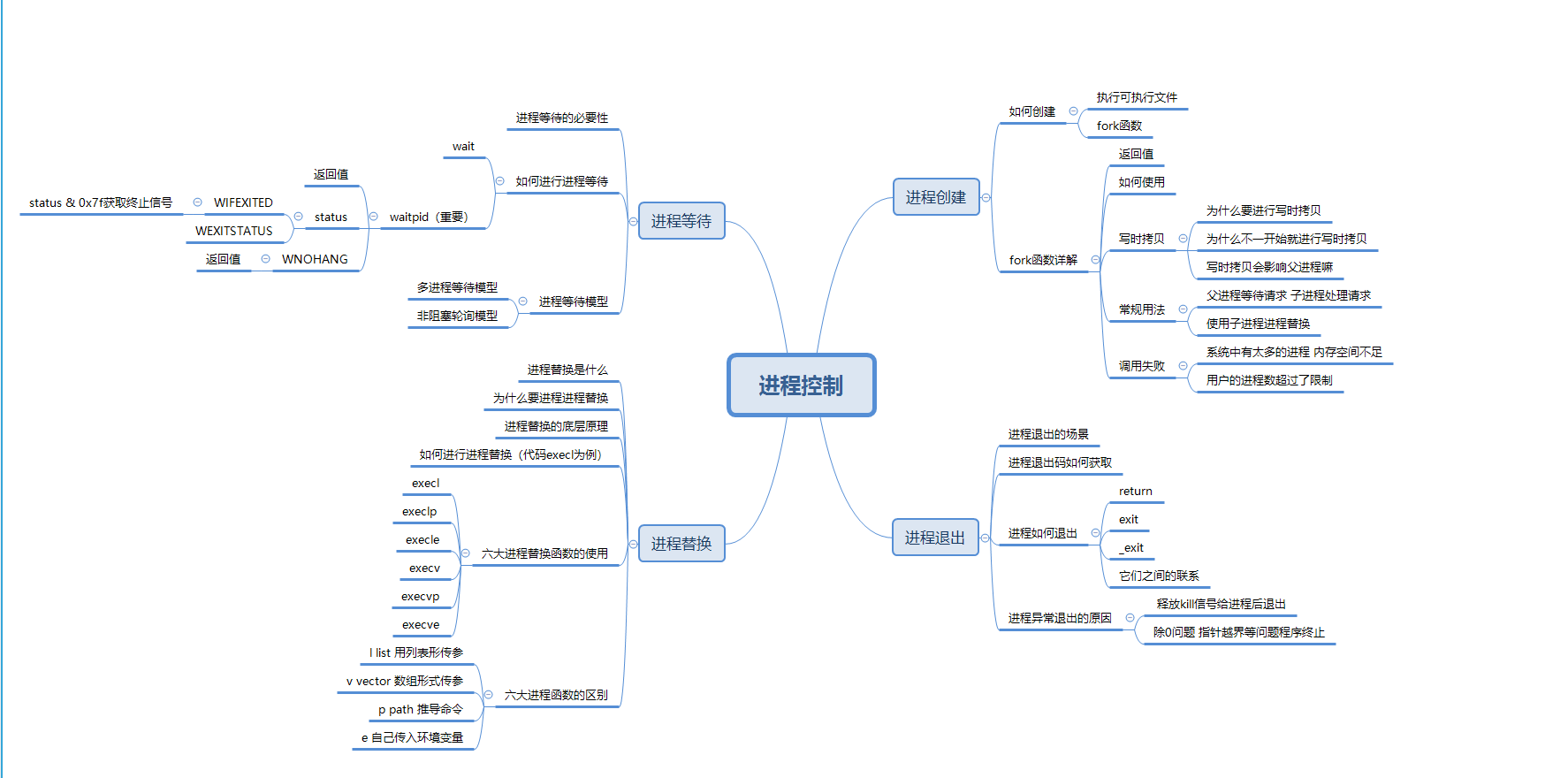
【Hello Linux】进程控制 (内含思维导图)
作者:小萌新 专栏:Linux 作者简介:大二学生 希望能和大家一起进步! 本篇博客简介:简单介绍下进程的控制 包括进程启动 进程终止 进程等待 进程替换等概念 进程控制介绍进程创建fork函数fork函数的返回值fork函数的使用…...

嵌入式linux物联网毕业设计项目智能语音识别基于stm32mp157开发板
stm32mp157开发板FS-MP1A是华清远见自主研发的一款高品质、高性价比的Linux单片机二合一的嵌入式教学级开发板。开发板搭载ST的STM32MP157高性能微处理器,集成2个Cortex-A7核和1个Cortex-M4 核,A7核上可以跑Linux操作系统,M4核上可以跑FreeRT…...
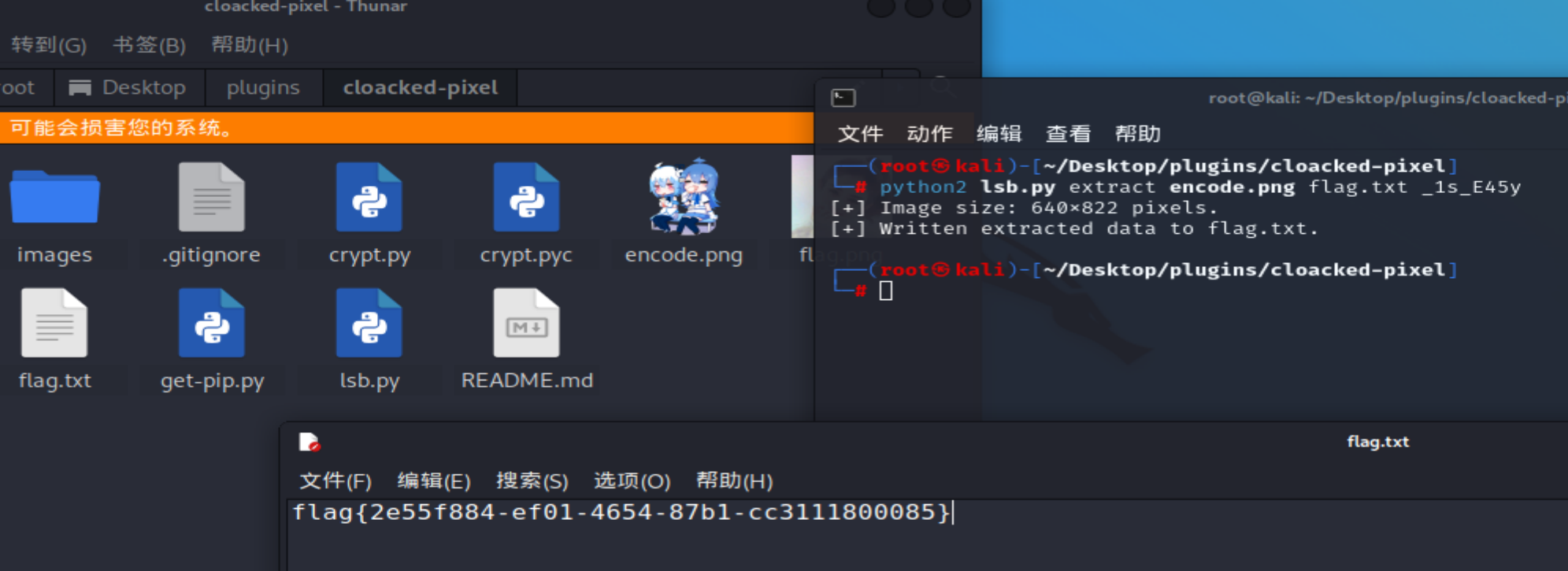
【黄河流域公安院校网络空间安全技能挑战赛】部分wp
文章目录webbabyPHPfunnyPHPEzphp**遍历文件目录的类**1、DirectoryIterator:2、FilesystemIterator:3、**Globlterator**读取文件内容的类:SplFileObjectMisc套娃web babyPHP <?php highlight_file(__FILE__); error_reporting(0);$num $_GET[nu…...

五点CRM系统核心功能是什么
很多企业已经把CRM客户管理系统纳入信息化建设首选,用于提升核心竞争力,改善企业市场、销售、服务、渠道和客户管理等几个方面,并进行创新或转型。CRM系统战略的五个关键要点是:挖掘潜在客户、评估和培育、跟进并成交、分析并提高…...
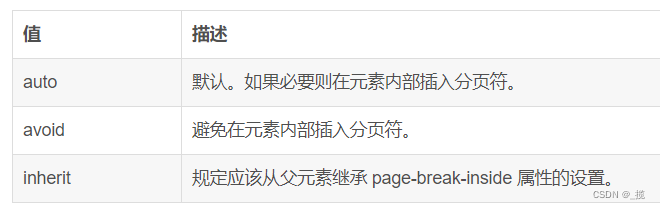
window.print() 前端实现网页打印详解
目录 前言 一、print()方法 二、打印样式 2.1使用打印样式表 2.2使用媒介查询 2.3内联样式使用media属性 2.4在css中使用import引入打印样式表 三、打印指定区域部分内容 3.1方法一 3.2方法二 3.3方法三 四、强制插入分页 4.1page-break-before(指定元素前…...

php程序员应具有的7种能力
php程序员应具有什么样的能力,才能更好的完成工作,才会有更好的发展方向呢?在中国我想您不会写一辈子代码的,那样不可能,过了黄金期,您又怎么办呢?看了本文后,希望对您有所帮助。 一…...
quarkus 生产环境与k8s集成总结
quarkus 生产环境与k8s集成总结 大纲 基础准备quarkus2.13.7脚手架工程配置GraalVM-java11 安装配置配置maven3.8.7linux环境下云原生二进制文件打包环境搭建编译运行quarkus二进制文件quarkus二进制文件制作为docker镜像并运行使用k8s部署quarkus二进制文件 基础准备 生产…...
蓝桥杯训练day2
day21.二分(1)789. 数的范围(2)四平方和(1)哈希表做法(2)二分做法(3)1227. 分巧克力(4)113. 特殊排序(5)1460. 我在哪?2.双指针(1)1238. 日志统计(2)1240. 完全二叉树的权值(3&#…...

为什么99%的程序员都做不好SQL优化?
连接层 最上层是一些客户端和链接服务,包含本地sock 通信和大多数基于客户端/服务端工具实现的类似于 TCP/IP的通信。主要完成一些类似于连接处理、授权认证、及相关的安全方案。在该层上引入了线程 池的概念,为通过认证安全接入的客户端提供线程。同样…...

Jenkins最新版安装调试
清理旧的jenkins: find / -name jenkins* 一项一项的清理:rm -rf /var/log/jenkins* 下载最新版jenkins镜像:jenkins-redhat-stable安装包下载_开源镜像站-阿里云 上传到服务器: 安装命令: yum install -y jenkins…...

简略说一下go的sync.RWMutex锁
在简略的说之前,首先要对RW锁的结构有一个大致的了解 type RWMutex struct {w Mutex // 写锁互斥锁,只锁写锁,和读锁无关writerSem uint32 // sema锁--用于“写协程”排队等待readerSem uint32 // sema锁--用于“读协程”排队…...

软考马上要报名了,出现这些问题怎么办?
目前,四川、山东、山西、辽宁、河北等地已经率先发布了2023年上半年软考报名通知。 四川:2023年3月13日-4月4日 山东:2023年3月17日9:00-4月3日16:00 山西:2023年3月14日9:00-3月28日11:00 辽宁:2023年3月14日8:30…...
)
单链表(增删查改)
目录一、什么是单链表?二、单链表的增删查改2.1 结构体变量的声明2.2 申请新结点2.2 链表的头插2.3 链表的尾插2.4 链表的头删2.5 链表的尾删2.6 链表的查找2.7 链表的任意位置后面插入2.8 链表的任意位置后面删除2.9 链表的销毁2.10 链表的打印三、代码汇总3.1 SLi…...

端口复用(bind error: Address already in use 问题)
欢迎关注博主 Mindtechnist 或加入【Linux C/C/Python社区】一起探讨和分享Linux C/C/Python/Shell编程、机器人技术、机器学习、机器视觉、嵌入式AI相关领域的知识和技术。 端口复用专栏:《Linux从小白到大神》《网络编程》 在前面讲解TCP状态转换中提到过一个2MSL…...
数字化引领乡村振兴,VR全景助力数字乡村建设
一、数字乡村建设加速经济发展随着数字化建设的推进,数字化农业产业正在成为农业产业发展的主导力量,因此数字化技术赋予农业产业竞争力的能力不可小觑。数字化乡村建设背景下,数字化信息技术将全面改造升级农村产业,从农业、养殖…...
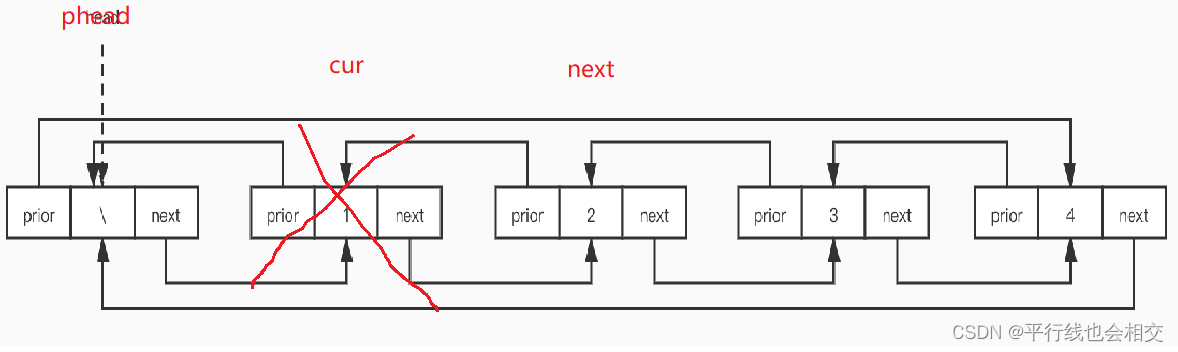
【数据结构入门】-链表之双向循环链表
个人主页:平行线也会相交 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【数据结构初阶(C实现)】 文章目录链表初始化打印链表尾插尾删新建一个节点头插头删查找在pos之前插入*删除pos位…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
