数据结构(六)——图
六、图
6.1 图的基本概念
图的定义
图:图G由顶点集V和边集E组成,记为G = (V, E),其中V(G)表示图G中顶点的有限非空集;E(G) 表示图G中顶点之间的关系(边)集合。若V = {v1, v2, … , vn},则用|V|表示图G中顶点的个 数,也称图G的阶,,用|E|表示图G中边的条数。
注意:线性表可以是空表,树可以是空树,但图不可以是空,即V一定是非空集
无向图:若E是无向边(简称边)的有限集合时,则图G为无向图。边是顶点的无序对,记为(v, w)或(w, v),因为(v, w) = (w, v),其 中v、w是顶点。可以说顶点w和顶点v互为邻接点。边(v, w) 依附于顶点w和v,或者说边(v, w)和顶点v、w相关联
有向图:若E是有向边(也称弧)的有限集合时,则图G为有向图。 弧是顶点的有序对,记为<v,w>,其中v、w是顶点,v称为弧尾,w称为弧头,<v,w>称为从顶点v到顶点w的弧,也称 v邻接到w,或w邻接自v。<v,w> ≠<w,v>

简单图——① 不存在重复边; ② 不存在顶点到自身的边 (数据结构课程只探讨 “简单图”)
多重图——图G中某两个结点之间的边数多于一条,又允许顶点通过同一条边和自己关联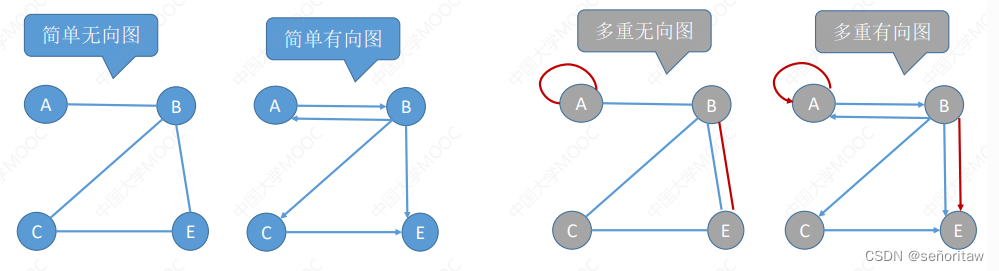
顶点的度、入度、出度
无向图:顶点v的度是指依附于该顶点的边的条数,记为TD(v)。
在具有n个顶点、e条边的无向图中,![]() 即无向图的全部顶点的度的和等于边数的2倍
即无向图的全部顶点的度的和等于边数的2倍
有向图:入度是以顶点v为终点的有向边的数目,记为ID(v);
出度是以顶点v为起点的有向边的数目,记为OD(v)。
顶点v的度等于其入度和出度之和,即TD(v) = ID(v) + OD(v)。
在具有n个顶点、e条边的有向图中,![]() ,即入度和出度的数量相等且等于e
,即入度和出度的数量相等且等于e
顶点的关系描述
路径——顶点vp到顶点vq之间的一条路径是指顶点序列,![]()
回路——第一个顶点和最后一个顶点相同的路径称为回路或环
简单路径——在路径序列中,顶点不重复出现的路径称为简单路径。
简单回路——除第一个顶点和最后一个顶点外,其余顶点不重复出现的回路称为简单回路。
路径长度——路径上边的数目
点到点的距离——从顶点u出发到顶点v的最短路径若存在,则此路径的长度称为从u到v的距离。 若从u到v根本不存在路径,则记该距离为无穷(∞)。
无向图中,若从顶点v到顶点w有路径存在,则称v和w是连通的
有向图中,若从顶点v到顶点w和从顶点w到顶点v之间都有路径,则称这两个顶点是强连通的
图G中任意两个顶点都是连通的,则称图G为连通图,否则称为非连通图。
若图中任何一对顶点都是强连通的,则称此图为强连通图。
研究图的局部—子图、生成子图
设有两个图G = (V, E)和G ′ = (V ′ , E ′ ),若V ′ 是V的子集,且 E ′ 是 E的子集,则称G ′ 是G的子图
若有满足V(G ′ ) = V(G)的子图G ′ ,则称其为G的生成子图
有向图的子图和生成子图也是一样的
无向图中的极大连通子图称为连通分量
子图必须连通,且包含尽可能多的顶点和边
有向图中的极大强连通子图称为有向图的强连通分量
子图必须强连通,同时 保留尽可能多的边
生成树:连通图的生成树是包含图中全部顶点的一个极小连通子图。
若图中顶点数为n,则它的生成树含有 n-1 条边。对生成树而言,若砍去它的一条边,则会变成非连通 图,若加上一条边则会形成一个回路。(因此边要尽可能的少,但要保持连通)
生成森林:在非连通图中,连通分量的生成树构成了非连通图的生成森林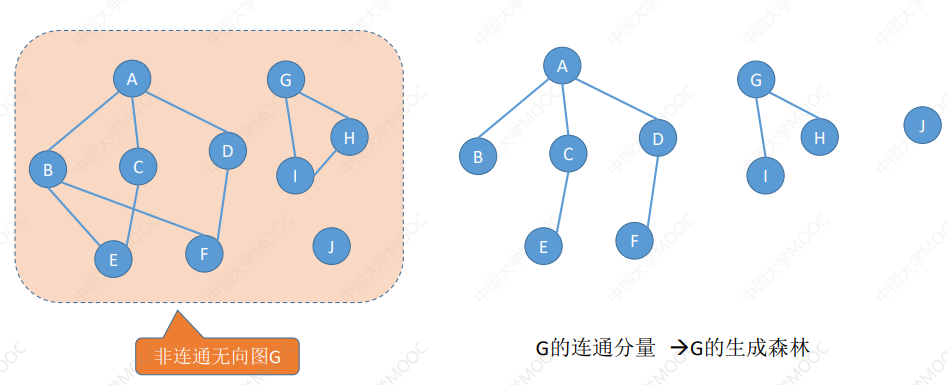
边的权、带权图/网
边的权——在一个图中,每条边都可以标上具有某种含义的数值,该数值称为该边的权值。
带权图/网——边上带有权值的图称为带权图,也称网。
带权路径长度——当图是带权图时,一条路径上所有边的权值之和,称为该路径的带权路径长度
特殊形态的图
无向完全图——无向图中任意两个顶点之间都存在边
若无向图的顶点数|V|=n,则
有向完全图——有向图中任意两个顶点 之间都存在方向相反的两条弧
若有向图的顶点数|V|=n,则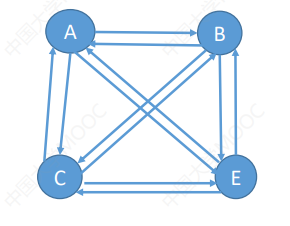
稀疏图:边数很少的图称为稀疏图 反之称为稠密图
树——不存在回路,且连通的无向图
n个顶点的树,必有n-1条边。
常见考点:n个顶点的图,若 |E|>n-1,则一定有回路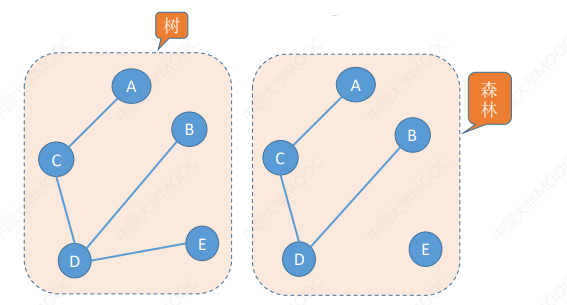
有向树——一个顶点的入度为0、其余顶点的 入度均为1的有向图,称为有向树

相关文章:

数据结构(六)——图
六、图 6.1 图的基本概念 图的定义 图:图G由顶点集V和边集E组成,记为G (V, E),其中V(G)表示图G中顶点的有限非空集;E(G) 表示图G中顶点之间的关系(边)集合。若V {v1, v2, … , vn},则用|V|…...

Android-AR眼镜屏幕显示
Android-AR眼镜 前提:Android手持设备 需要具备DP高清口 1、创建Presentation(双屏异显) public class MyPresentation extends Presentation {private PreviewSingleBinding binding;private ScanActivity activity;public MyPresentatio…...

蓝桥集训之货币系统
蓝桥集训之货币系统 核心思想:背包 #include <iostream>#include <cstring>#include <algorithm>using namespace std;const int N 30,M 10010;typedef long long LL;LL f[M];int w[N];int n,m;int main(){cin>>n>>m;for(int i1;i&…...

基于微信小程序的校园服务平台设计与实现(程序+论文)
本文以校园服务平台为研究对象,首先分析了当前校园服务平台的研究现状,阐述了本系统设计的意义和背景,运用微信小程序开发工具和云开发技术,研究和设计了一个校园服务平台,以满足学生在校园生活中的多样化需求。通过引…...
QT+Opencv+yolov5实现监测
功能说明:使用QTOpencvyolov5实现监测 仓库链接:https://gitee.com/wangyoujie11/qt_yolov5.git git本仓库到本地 一、环境配置 1.opencv配置 将OpenCV-MinGW-Build-OpenCV-4.5.2-x64文件夹放在自己的一个目录下,如我的路径: …...

【Python-Docx库】Word与Python的完美结合
【Python-Docx库】Word与Python的完美结合 今天给大家分享Python处理Word的第三方库:Python-Docx。 什么是Python-Docx? Python-Docx是用于创建和更新Microsoft Word(.docx)文件的Python库。 日常需要经常处理Word文档…...
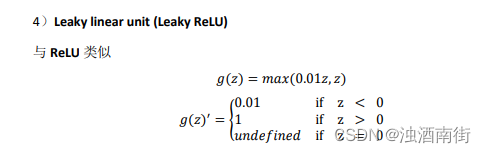
吴恩达深度学习笔记:浅层神经网络(Shallow neural networks)3.6-3.8
目录 第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)第三周:浅层神经网络(Shallow neural networks)3.6 激活函数(Activation functions)3.7 为什么需要非线性激活函数?(why need a non…...

盘点最适合做剧场版的国漫,最后一部有望成为巅峰
最近《完美世界》动画官宣首部剧场版,主要讲述石昊和火灵儿的故事。这个消息一出,引发了很多漫迷的讨论,其实现在已经有好几部国漫做过剧场版,还有是观众一致希望未来会出剧场版的。那么究竟是哪些国漫呢,下面就一起来…...

Altium Designer许可需求分析
在电子设计的世界中,Altium Designer已成为设计师们的得力助手。然而,如何进行有效的许可需求分析,以确保软件的高效使用和企业的可持续发展?本文将带您了解如何进行Altium Designer的许可需求分析,让您在设计的道路上…...

[c++]类和对象常见题目详解
本专栏内容为:C学习专栏,分为初阶和进阶两部分。 通过本专栏的深入学习,你可以了解并掌握C。 💓博主csdn个人主页:小小unicorn ⏩专栏分类:C 🚚代码仓库:小小unicorn的代码仓库&…...
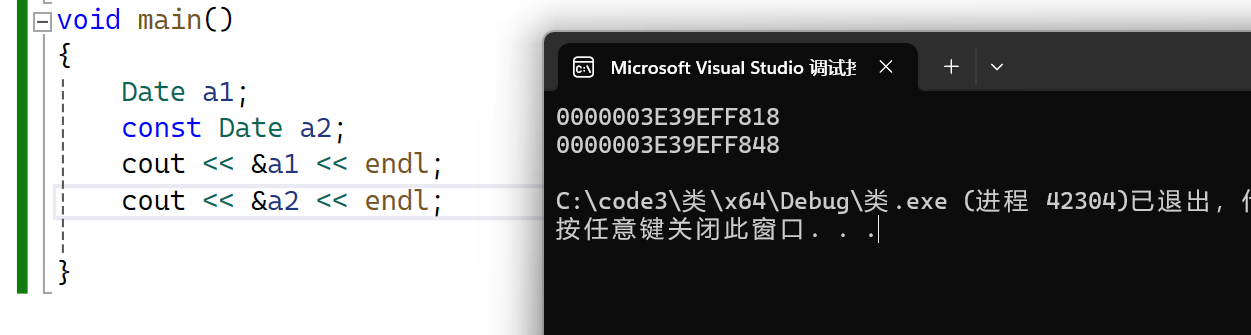
【c++】类和对象(五)赋值运算符重载
🔥个人主页:Quitecoder 🔥专栏:c笔记仓 朋友们大家好,本篇文章带大家认识赋值运算符重载,const成员,取地址及const取地址操作符重载等内容 目录 1.赋值运算符重载1.1运算符重载1.1.1特性&#…...
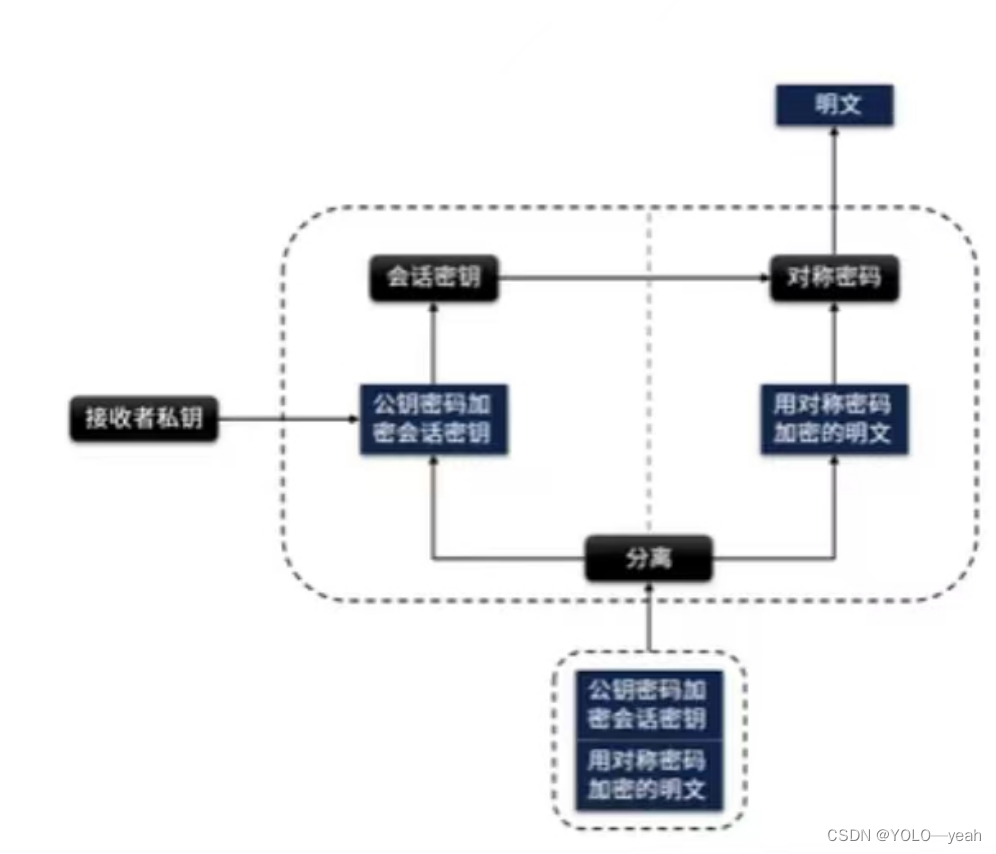
密码学基础-对称密码/公钥密码/混合密码系统 详解
密码学基础-对称密码/公钥密码 加解密说明1.加密解密必要因素加密安全性说明 什么是对称密码图示说明对称密码详解什么是DES?举例说明 什么是3DES什么是AES? 公钥密码什么是RSA? 对称密钥和公钥密码优缺点对比对称密码对称密码算法总结对称密码存在的问题? 公钥密码公钥密码…...
》)
《装饰器模式(极简c++)》
本文章属于专栏- 概述 - 《设计模式(极简c版)》-CSDN博客 模式说明: 方案: 装饰类和派生类同根,然后装饰类中放一个派生类,以在接口不动的情况下增加功能优点: 可以灵活地扩展对象功能…...

Spring Boot 整合分布式搜索引擎 Elastic Search 实现 自动补全功能
文章目录 ⛄引言一、分词器⛅拼音分词器⚡自定义分词器 二、自动补全查询三、自动补全⌚业务需求⏰实现酒店搜索自动补全 四、效果图⛵小结 ⛄引言 本文参考黑马 分布式Elastic search Elasticsearch是一款非常强大的开源搜索引擎,具备非常多强大功能,…...
实现一个Google身份验证代替短信验证
最近才知道公司还在做国外的业务,要实现一个登陆辅助验证系统。咱们国内是用手机短信做验证,当然 这个google身份验证只是一个辅助验证登陆方式。看一下演示 看到了嘛。 手机下载一个谷歌身份验证器就可以 。 谷歌身份验证器,我本身是一个基…...

Spring框架与Spring Boot的区别和联系
引言 Spring框架和Spring Boot都是Java生态中最受欢迎的开源框架,它们各自扮演着不同的角色,帮助开发者构建高效的企业级应用。本教程将从零基础的角度出发,让你轻松理解这两者的区别和联系。 Spring框架简介 Spring框架,简称Spri…...

[OpenCV学习笔记]Qt+OpenCV实现图像灰度反转、对数变换和伽马变换
目录 1、介绍1.1 灰度反转1.2 图像对数变换1.3 图像伽马变换 2、效果图3、代码实现4、源码展示 1、介绍 1.1 灰度反转 灰度反转是一种线性变换,是将某个范围的灰度值映射到另一个范围内,一般是通过灰度的对调,突出想要查看的灰度区间。 S …...

【大数据】Flink学习笔记
文章目录 认识FlinkDocker安装Flink基本概念Flink的特点Flink 和 Spark Streaming 对比 基本使用WordCount实现依赖 批模式代码流模式代码网络流模式代码在web UI上提交代码创建项目[^1]编写代码配置打包在Web UI上提交 Flink 架构系统架构核心概念并行度算子链(Opeartor Chain…...

社交网络的未来:Facebook如何塑造数字社交的下一章
引言 社交网络已成为我们生活中不可或缺的一部分,而Facebook作为其领军者,一直在塑造着数字社交的未来。本文将深入探讨Facebook在未来如何塑造数字社交的下一章,并对社交网络的发展趋势进行展望和分析。 1. 引领虚拟社交的潮流 Facebook将…...
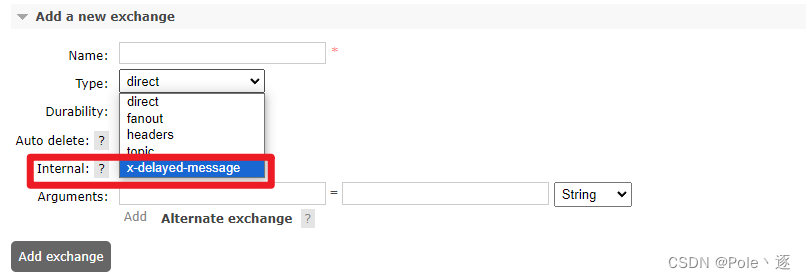
RabbitMQ 延时消息实现
1. 实现方式 1. 设置队列过期时间:延迟队列消息过期 死信队列,所有消息过期时间一致 2. 设置消息的过期时间:此种方式下有缺陷,MQ只会判断队列第一条消息是否过期,会导致消息的阻塞需要额外安装 rabbitmq_delayed_me…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

Linux入门(十五)安装java安装tomcat安装dotnet安装mysql
安装java yum install java-17-openjdk-devel查找安装地址 update-alternatives --config java设置环境变量 vi /etc/profile #在文档后面追加 JAVA_HOME"通过查找安装地址命令显示的路径" #注意一定要加$PATH不然路径就只剩下新加的路径了,系统很多命…...
