数值代数及方程数值解:预备知识——二进制及浮点数
文章目录
- 二进制
- IEEE浮点数
本篇文章的前置知识:数学分析
二进制
命题:二进制转化为十进制
二进制的数字表示为 ⋯ b 2 b 1 b 0 . b − 1 b − 2 ⋯ \cdots b_2b_1b_0.b_{-1}b_{-2}\cdots ⋯b2b1b0.b−1b−2⋯这等价于十进制下的
⋯ b 2 × 2 2 + b 1 × 2 1 + b 0 × 2 0 + b − 1 × 2 − 1 + b − 2 × 2 − 2 + ⋯ \cdots b_2\times 2^{2}+b_1\times 2^{1}+b_0\times 2^0+b_{-1}\times 2^{-1}+b_{-2}\times 2^{-2}+\cdots ⋯b2×22+b1×21+b0×20+b−1×2−1+b−2×2−2+⋯
命题:十进制转化为二进制
整数部分:十进制整数不断除2,记录除数及余数,直至除数为0,从后往前依次写下余数即为二进制下的数字,如下例 ( 53 ) 10 (53)_{10} (53)10
53 ÷ 2 = 26 余 1 26 ÷ 2 = 13 余 0 13 ÷ 2 = 6 余 1 6 ÷ 2 = 3 余 0 3 ÷ 2 = 1 余 1 1 ÷ 2 = 0 余 1 53\div 2= 26 \text{余} 1\\ 26\div 2=13 \text{余} 0\\ 13\div 2=6 \text{余} 1\\ 6\div 2=3 \text{余} 0\\ 3\div 2=1 \text{余} 1\\ 1\div 2=0 \text{余} 1 53÷2=26余126÷2=13余013÷2=6余16÷2=3余03÷2=1余11÷2=0余1则得 ( 53 ) 10 = ( 110101. ) 2 (53)_{10}=(110101.)_2 (53)10=(110101.)2
小数部分:十进制小数不断乘2,记录整数部分,从前往后依次写下整数部分,如下例 ( 0.7 ) 10 (0.7)_{10} (0.7)10
0.7 × 2 = 0.4 + 1 0.4 × 2 = 0.8 + 0 0.8 × 2 = 0.6 + 1 0.6 × 2 = 0.2 + 1 0.2 × 2 = 0.4 + 0 ⋯ 0.7\times 2=0.4+1\\ 0.4\times 2=0.8+0\\ 0.8\times 2=0.6+1\\ 0.6\times 2=0.2+1\\ 0.2\times 2=0.4 +0\\ \cdots 0.7×2=0.4+10.4×2=0.8+00.8×2=0.6+10.6×2=0.2+10.2×2=0.4+0⋯发现计算过程开始循环,故 ( 0.7 ) 10 = ( 0.1 0110 ‾ ) 2 (0.7)_{10}=(0.1\overline{0110})_2 (0.7)10=(0.10110)2
IEEE浮点数
定义:IEEE浮点数
标准的IEEE浮点数为 ± 1. a b c d e f g … z × 2 p \pm 1.abcdefg\dots z \times 2^p ±1.abcdefg…z×2p其中 a b c d e f g … z abcdefg\dots z abcdefg…z 取值只有 0 或 1
该浮点数在计算机中的储存方式为 1 a b c d e f g … z p 1\hspace{1ex} abcdefg\dots z\hspace{1ex}p 1abcdefg…zp
其中
- 首位表示正负号,0代表正数,1代表负数
- 后面部分称为尾数,是有效数字
- 中间部分称为指数,指明小数点的位置
例如:9的2进制表示为1001,浮点数表示为0 11 001,第一个数 0 表示该数为正数,尾数001表示这个数的有效数字为 ( 1.001 ) 2 (1.001)_2 (1.001)2(默认首位为1),第二个数 ( 11 ) 2 = 3 (11)_2=3 (11)2=3表示这个数的指数为3,即把小数点向右移动3位
定义:一般的浮点数系统(描述性定义)
考虑 R \mathbb{R} R 的某离散子集 F \mathrm{F} F, F \mathrm{F} F的元素形如 0 或 x = ± m β t β e x=\pm \dfrac{m}{\beta^t}\beta^e x=±βtmβe,其中
- β \beta β 为不小于2的整数,称为基数;(即 β \beta β 进制)
- t t t 为不大于1的整数,称为精度;(即该系统能表示的最大位数尾数)
- m ∈ [ 1 , β t ] m\in[1,\beta^t] m∈[1,βt]是整数,e为任意整数(即指数);
- 若限制 m m m 的范围为 [ β t − 1 , β t − 1 ] [\beta^{t-1},\beta^t-1] [βt−1,βt−1],则可使 m m m 唯一;此时 ± ( m β t ) \pm(\dfrac{m}{\beta^t}) ±(βtm) 称为 x x x 的尾数;
注:对于那些位数超过精度的数字,必须进行截断并舍入(零舍一入),才能保存在计算机中,故浮点数集 F F F 在实数 R \mathbb{R} R 中是离散的
定义:机器 ϵ \epsilon ϵ
ε m a c h i n e = 1 2 β 1 − t \varepsilon_{machine}=\dfrac{1}{2}\beta^{1-t} εmachine=21β1−t表示两个相邻的浮点数之间的距离的一半
注:有的书上也定义为两个相邻的浮点数之间的距离
定义:单精度、双精度浮点数
单精度浮点数:1位符号,8位指数,23位尾数, ε m a c h i n e = 2 − 24 \varepsilon_{machine}=2^{-24} εmachine=2−24
双精度浮点数:1位符号,11位指数,52位尾数, ε m a c h i n e = 2 − 53 \varepsilon_{machine}=2^{-53} εmachine=2−53
注:
单精度浮点数也称 32 位浮点数 1 + 8 + 23 = 32 1+8+23=32 1+8+23=32
双精度浮点数也称 64 位浮点数 1 + 11 + 52 = 64 1+11+52=64 1+11+52=64
定义:浮点数函数
令 f l : R → F fl:\mathbb{R}\to F fl:R→F 表示将实数映射为离它最近的浮点数的函数
命题:用浮点数保存实数的舍入误差
∀ x ∈ R , ∣ x − f l ( x ) ∣ ∣ x ∣ ≤ ε m a c h i n e \forall x\in\mathbb{R},\dfrac{|x-fl(x)|}{|x|}\leq \varepsilon_{machine} ∀x∈R,∣x∣∣x−fl(x)∣≤εmachine或等价地说,
∀ x ∈ R , ∃ ϵ , ∣ ϵ ∣ ≤ ε m a c h i n e , s . t . f l ( x ) = x ( 1 + ϵ ) \forall x\in\mathbb{R},\exists \epsilon,|\epsilon|\leq\varepsilon_{machine},s.t.fl(x)=x(1+\epsilon) ∀x∈R,∃ϵ,∣ϵ∣≤εmachine,s.t.fl(x)=x(1+ϵ)
浮点数运算的基本公理
任取 x , y ∈ F x,y\in F x,y∈F,令 ∗ \ast ∗ 表示四则运算的任一个, ⊛ \circledast ⊛ 表示相应的浮点数的四则运算,则 x ⊛ y = f l ( x + y ) x\circledast y=fl(x+y) x⊛y=fl(x+y)
等价地,有如下的浮点数运算公理:
∀ x , y ∈ F , ∃ ϵ , ∣ ϵ ∣ ≤ ε m a c h i n e , s . t . x ⊛ y = ( x ∗ y ) ( 1 + ϵ ) \forall x,y\in F,\exists \epsilon,|\epsilon|\leq\varepsilon_{machine},s.t.x\circledast y=(x\ast y)(1+\epsilon) ∀x,y∈F,∃ϵ,∣ϵ∣≤εmachine,s.t.x⊛y=(x∗y)(1+ϵ)
注: ε m a c h i n e \varepsilon_{machine} εmachine定义的修正:将 ε m a c h i n e \varepsilon_{machine} εmachine定义为满足上述公理的最小值,这样定义不会对运算产生显著影响
一般来说,我们使用的计算机是符合浮点数运算的基本公理的
参考书籍
《数值分析》Timothy Sauer 著,裴玉茹,马赓宇 译
《Numerical Linear Algebra》Lloyd N.Trefethen , David Bau 著
相关文章:

数值代数及方程数值解:预备知识——二进制及浮点数
文章目录 二进制IEEE浮点数 本篇文章的前置知识:数学分析 二进制 命题:二进制转化为十进制 二进制的数字表示为 ⋯ b 2 b 1 b 0 . b − 1 b − 2 ⋯ \cdots b_2b_1b_0.b_{-1}b_{-2}\cdots ⋯b2b1b0.b−1b−2⋯这等价于十进制下的 ⋯ b 2 2 …...

新数字时代的启示:揭开Web3的秘密之路
在当今数字时代,随着区块链技术的不断发展,Web3作为下一代互联网的概念正逐渐引起人们的关注和探索。本文将深入探讨新数字时代的启示,揭开Web3的神秘之路,并探讨其在未来的发展前景。 1. Web3的定义与特点 Web3是对互联网未来发…...

算法——动态规划:01背包
原始01背包见下面这篇文章:http://t.csdnimg.cn/a1kCL 01背包的变种:. - 力扣(LeetCode) 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。 简化一…...

写作类AI推荐(二)
本章要介绍的写作AI如下: 火山写作 主要功能: AI智能创作:告诉 AI 你想写什么,立即生成你理想中的文章AI智能改写:选中段落句子,可提升表达、修改语气、扩写、总结、缩写等文章内容优化:根据全文…...
(JAVA))
分寝室(20分)(JAVA)
目录 题目描述 输入格式: 输出格式: 输入样例 1: 输出样例 1: 输入样例 2: 输出样例 2: 题解: 题目描述 学校新建了宿舍楼,共有 n 间寝室。等待分配的学生中,有女…...

Spring 源码调试问题 ( List.of(“bin“, “build“, “out“); )
Spring 源码调试问题 文章目录 Spring 源码调试问题一、问题描述二、解决方案 一、问题描述 错误:springframework\buildSrc\src\main\java\org\springframework\build\CheckstyleConventions.java:68: 错误: 找不到符号 List<String> buildFolders List.of…...
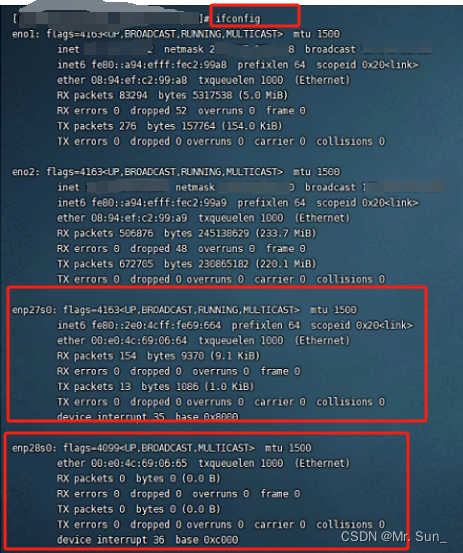
Centos7安装RTL8111网卡驱动
方法一: // 安装pciutils # yum install -y pciutils // 查看pci设备信息 # lspci | grep -i Ethernet 09:00.0 Ethernet controller: Realtek Semiconductor Co., Ltd. RTL8111/8168/8411 PCI Express Gigabit Ethernet Controller (rev 03) // 上面看到是Re…...

吉时利KEITHLEY2460数字源表
181/2461/8938产品概述: Keithley 2460 高电流源表源测量单元 (SMU) 将先进的触摸、测试和发明技术带到您的指尖。Keithley 2460 将创新的图形用户界面 (GUI) 与电容式触摸屏技术相结合,使测试变得直观并最大限度地缩短学习曲线,从而帮助工程…...
)
数据库原理(含思维导图)
数据库原理笔记,html与md笔记已上传 1.绪论 发展历程 记住数据怎么保存,谁保存数据,共享性如何,独立性如何 人工管理阶段 数据不保存应用程序管理数据数据不共享数据不具有独立性 文件系统阶段 数据可以长期保存文件系统管…...

数据结构(六)——图
六、图 6.1 图的基本概念 图的定义 图:图G由顶点集V和边集E组成,记为G (V, E),其中V(G)表示图G中顶点的有限非空集;E(G) 表示图G中顶点之间的关系(边)集合。若V {v1, v2, … , vn},则用|V|…...

Android-AR眼镜屏幕显示
Android-AR眼镜 前提:Android手持设备 需要具备DP高清口 1、创建Presentation(双屏异显) public class MyPresentation extends Presentation {private PreviewSingleBinding binding;private ScanActivity activity;public MyPresentatio…...

蓝桥集训之货币系统
蓝桥集训之货币系统 核心思想:背包 #include <iostream>#include <cstring>#include <algorithm>using namespace std;const int N 30,M 10010;typedef long long LL;LL f[M];int w[N];int n,m;int main(){cin>>n>>m;for(int i1;i&…...

基于微信小程序的校园服务平台设计与实现(程序+论文)
本文以校园服务平台为研究对象,首先分析了当前校园服务平台的研究现状,阐述了本系统设计的意义和背景,运用微信小程序开发工具和云开发技术,研究和设计了一个校园服务平台,以满足学生在校园生活中的多样化需求。通过引…...
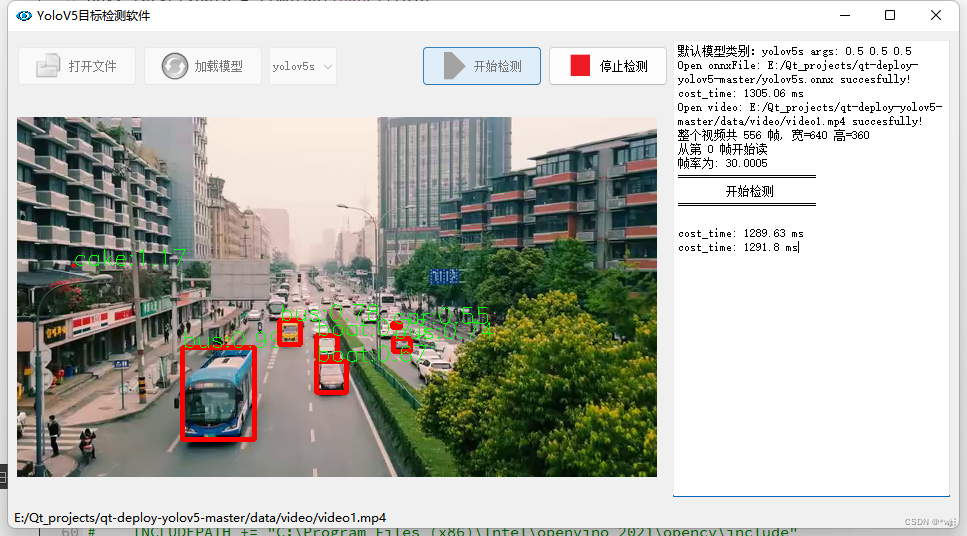
QT+Opencv+yolov5实现监测
功能说明:使用QTOpencvyolov5实现监测 仓库链接:https://gitee.com/wangyoujie11/qt_yolov5.git git本仓库到本地 一、环境配置 1.opencv配置 将OpenCV-MinGW-Build-OpenCV-4.5.2-x64文件夹放在自己的一个目录下,如我的路径: …...

【Python-Docx库】Word与Python的完美结合
【Python-Docx库】Word与Python的完美结合 今天给大家分享Python处理Word的第三方库:Python-Docx。 什么是Python-Docx? Python-Docx是用于创建和更新Microsoft Word(.docx)文件的Python库。 日常需要经常处理Word文档…...
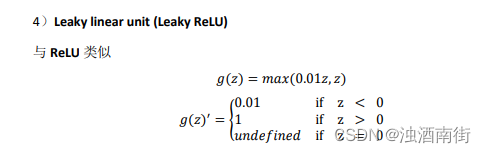
吴恩达深度学习笔记:浅层神经网络(Shallow neural networks)3.6-3.8
目录 第一门课:神经网络和深度学习 (Neural Networks and Deep Learning)第三周:浅层神经网络(Shallow neural networks)3.6 激活函数(Activation functions)3.7 为什么需要非线性激活函数?(why need a non…...

盘点最适合做剧场版的国漫,最后一部有望成为巅峰
最近《完美世界》动画官宣首部剧场版,主要讲述石昊和火灵儿的故事。这个消息一出,引发了很多漫迷的讨论,其实现在已经有好几部国漫做过剧场版,还有是观众一致希望未来会出剧场版的。那么究竟是哪些国漫呢,下面就一起来…...

Altium Designer许可需求分析
在电子设计的世界中,Altium Designer已成为设计师们的得力助手。然而,如何进行有效的许可需求分析,以确保软件的高效使用和企业的可持续发展?本文将带您了解如何进行Altium Designer的许可需求分析,让您在设计的道路上…...

[c++]类和对象常见题目详解
本专栏内容为:C学习专栏,分为初阶和进阶两部分。 通过本专栏的深入学习,你可以了解并掌握C。 💓博主csdn个人主页:小小unicorn ⏩专栏分类:C 🚚代码仓库:小小unicorn的代码仓库&…...
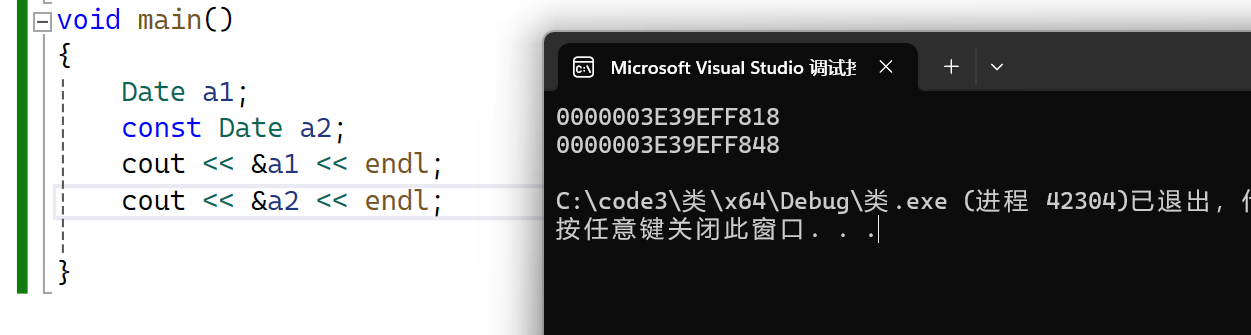
【c++】类和对象(五)赋值运算符重载
🔥个人主页:Quitecoder 🔥专栏:c笔记仓 朋友们大家好,本篇文章带大家认识赋值运算符重载,const成员,取地址及const取地址操作符重载等内容 目录 1.赋值运算符重载1.1运算符重载1.1.1特性&#…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
