Math类
java.lang.Math 提供了一系列静态方法用于科学计算,常用方法如下:
abs 绝对值
acos,asin,atan,cos,sin,tan 三角函数
sqrt 平方根
pow(double a,double b) a的b次幂
max(double a,double b) 取大值
min(double a,double b) 取小值
ceil(double a) 大于a的最小整数
floor(double a) 小于a的最大整数
random() 返回 0.0 到 1.0 的随机数
long round(double a) double 型的数据 a 转换为 long 型(四舍五入)
toDegrees(double angrad) 弧度->角度
toRadians(double angdeg) 角度->弧度
Math类的常用方法:
public class TestMath {public static void main(String[] args){//取整相关操作System.out.println(Math.ceil(3,2));System.out.println(Math.floor(3,2));System.out.println(Math.round(3,2));System.out.println(Math.round(3,8));//绝对值、开方、a的b次幂等操作System.out.println(Math.abs(-45));System.out.println(Math.sqrt(64));System.out.println(Math.pow(5,2));System.out.println(Math.pow(2,5));//Math类中常用的常量System.out.println(Math.PI);System.out.println(Math.E);//随机数System.out.println(Math.random()); //[0,1)}
}执行结果如图所示:

相关文章:

Math类
java.lang.Math 提供了一系列静态方法用于科学计算,常用方法如下: abs 绝对值 acos,asin,atan,cos,sin,tan 三角函数 sqrt 平方根 pow(double a,double b) a的b次幂 max(double a,double b) 取大…...

Git 入门教程
Git 入门教程 一、Git 是什么? Git 是一个开源的分布式版本控制系统,用于追踪代码的改动。它可以帮助开发者协同工作,管理项目中的代码版本。 二、安装 Git 在开始使用 Git 之前,你需要在你的计算机上安装 Git。你可以从 Git …...

Linux网络配置(超详细)
Linux网络配置大全 Linux网络配置一.网络地址配置网络地址查看–ifconfig使用网络配置命令设置网络接口参数-ifconfig禁用(临时)或者重新激活网卡设置虚拟网络接口 修改网络配置文件网络接口配置文件 IP命令详解OPTIONS选项OBJECT对象 ip link 二、获取和修改主机名hostname查看…...
[自研开源] 数据集成之分批传输 v0.7
开源地址:gitee | github 详细介绍:MyData 基于 Web API 的数据集成平台 部署文档:用 Docker 部署 MyData 使用手册:MyData 使用手册 试用体验:https://demo.mydata.work 交流Q群:430089673 介绍 本篇基于…...

用 AI 编程-释放ChatGPT的力量
最近读了本书,是 Sean A Williams 写的,感觉上还是相当不错的。一本薄薄的英文书,还真是写的相当好。如果你想看,还找不到,可以考虑私信我吧。 ChatGPT for Coders Unlock the Power of AI with ChatGPT: A Comprehens…...
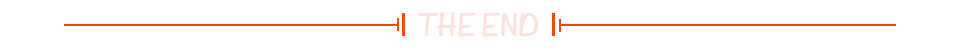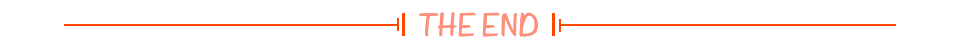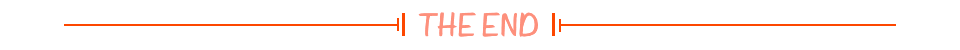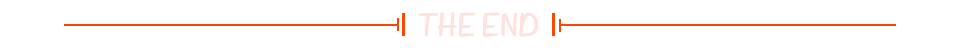
【快速解决】解决谷歌自动更新的问题,禁止谷歌自动更新,如何防止chrome自动升级 chrome浏览器禁止自动升级设置方法
目录 问题描述 解决方法 1、搜索栏搜索控制面板 2、搜索:服务 编辑 3、点击Windows工具 4、点击服务 5、禁止谷歌更新 问题描述 由于我现在需要装一个谷歌的驱动系统,但是目前的谷歌驱动系统的版本都太旧了,谷歌自身的版本又太新了…...

【Leetcode每日一题】模拟 - 替换所有的问号(难度⭐)(42)
1. 题目解析 题目链接:1576. 替换所有的问号 这个问题的理解其实相当简单,只需看一下示例,基本就能明白其含义了。 2.算法原理 遍历字符串:从左到右逐个处理字符。 处理问号字符:对于每个问号字符,我们需…...

再见 mysql_upgrade
在数据库管理的世界里,随着技术的不断进步和业务的不断发展,数据库的版本升级成为了一个不可避免的过程。 MySQL 作为业界领先的开源关系型数据库管理系统,其版本迭代与功能优化同样不容忽视。 而在这个过程中,升级工具就显得尤为…...

.NET Core教程:入门与实践实例
.NET Core教程:入门与实践实例 在信息技术飞速发展的今天,掌握一门高效的编程技术成为了每个开发者不可或缺的技能。在众多编程框架中,.NET Core以其跨平台、高性能和易扩展的特性,受到了广大开发者的青睐。本文将通过实例&#…...
docker环境配置过程中的常见问题
1、pull镜像问题 docker pull jenkins/jenkins:lts Using default tag: latest Trying to pull repository docker.io/library/centos ... Get https://registry-1.docker.io/v2/library/centos/manifests/latest: Get https://auth.docker.io/token?scoperepository%3Alibr…...
精选2024年最佳项目管理系统!实用推荐与详细评测
随着企业规模的扩大,项目量也会呈几何倍的增长,项目管理系统就成了企业管理必不可少的一部分。2024年优秀的项目管理系统推荐。今年为大家带来Microsoft Project、Zoho Projects、Jira以及Wrike项目管理系统评测。 什么是项目管理系统? 项目…...
民航电子数据库:CAEMigrator迁移数据库时总是卡死
目录 一、场景二、异常情况三、排查四、应急方案 一、场景 1、对接民航电子数据库 2、将mysql数据库迁移到cae数据库 3、使用CAEMigrator迁移工具进行数据库迁移时,该工具会卡死(不清楚是否是部署cae服务的服务器资源导致) 二、异常情况 …...
)
数据结构 第6章 图(一轮习题总结)
数据结构 第6章 图 6.1 图的基本概念6.2 图的存储及基本操作6.3 图的遍历6.4 图的应用 6.1 图的基本概念(2 4 11) 6.2 图的存储及基本操作(1 12 13 15 16) 6.3 图的遍历(2 3 5 16) 6.4 图的应用 6.1 图的基…...

如何在智能交通系统中使用物联网技术提高道路安全和效率
在智能交通系统中,物联网(IoT)技术可以通过多种方式提高道路安全和效率。以下是利用物联网技术提高智能交通系统效能的具体方法: 1. 车与路、车与车通信(V2X):通过在道路上部署传感器和路侧单元…...
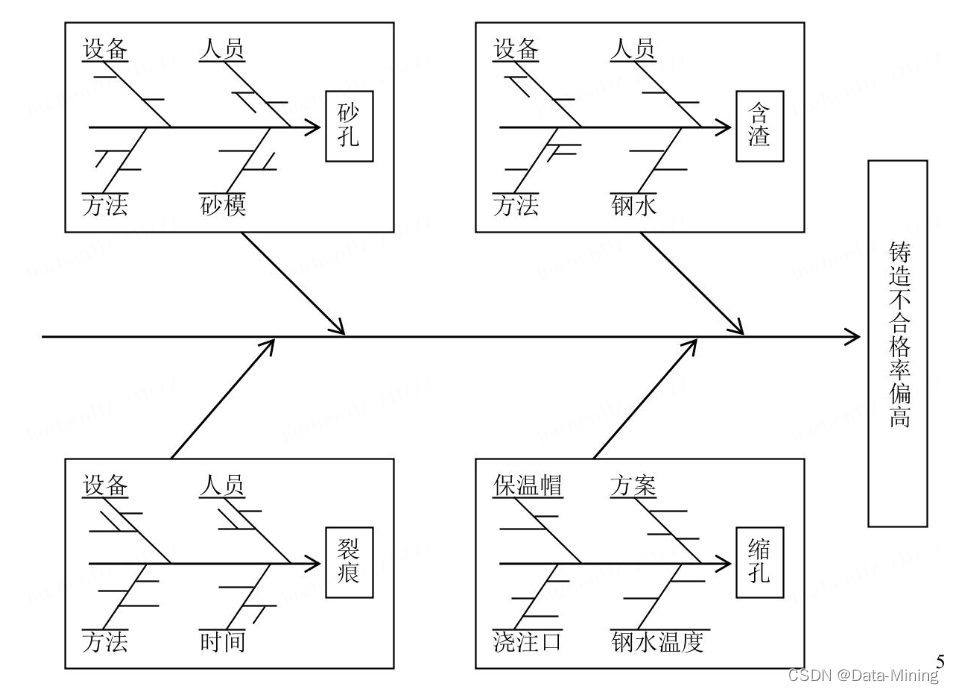
七大 QC 工具图的定义与示例(看这篇就够了)
前言 七大 QC 工具图是通过数值的方式进行数据分析的工具,分别是鱼骨图、直方图、柏拉图、散布图、管制图、检查图和层别图。其实,我们在日常生活与工作中经常看到它们,只是样子和名字对不上而已,今天写这篇文章就是为了帮助自己…...
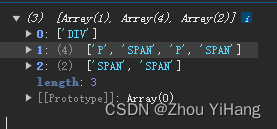
【JavaScript算法】DOM树层级显示
题目描述: 上述表达式的输出结果为 [DIV] [P, SPAN, P, SPAN] [SPAN, SPAN]直接上代码 let tree document.querySelector(".a"); function traverseElRoot(elRoot) {const result [];function traverse(element, level) {if (!result[level]) {resul…...
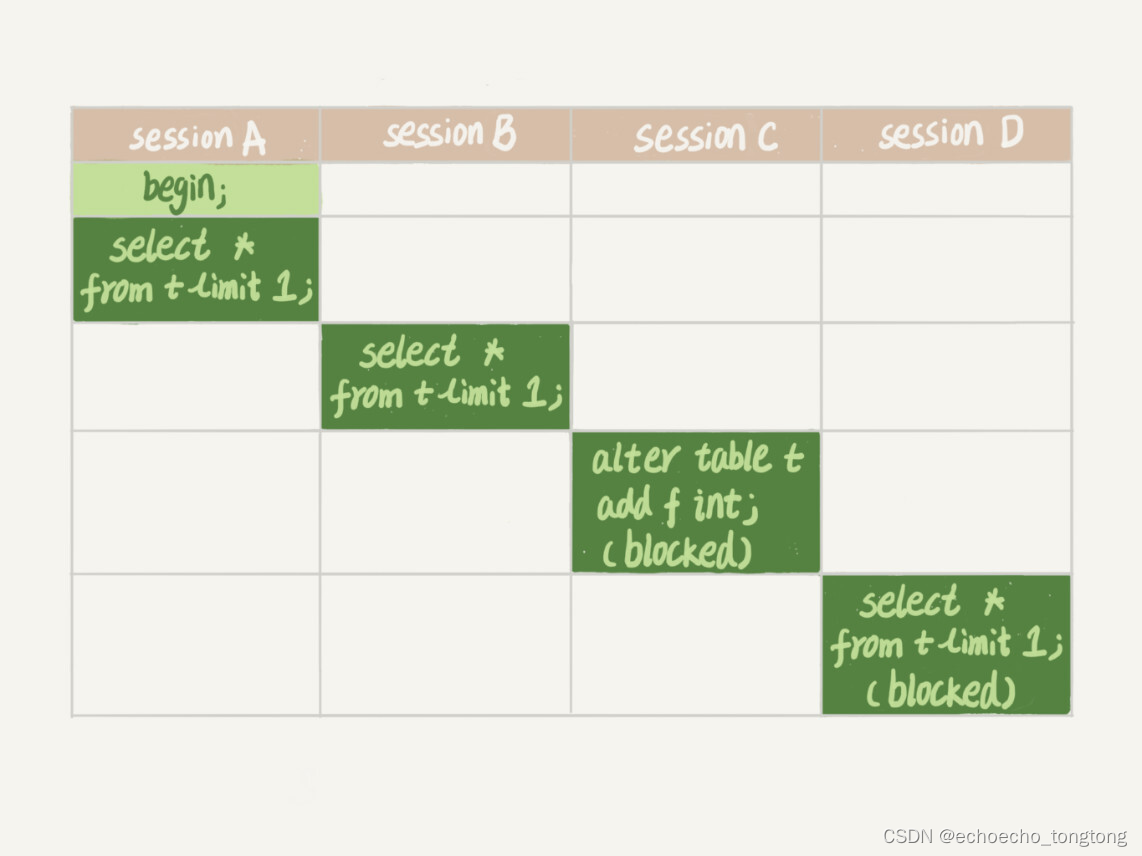
MySql实战--全局锁和表锁 :给表加个字段怎么有这么多阻碍
今天我要跟你聊聊MySQL的锁。数据库锁设计的初衷是处理并发问题。作为多用户共享的资源,当出现并发访问的时候,数据库需要合理地控制资源的访问规则。而锁就是用来实现这些访问规则的重要数据结构。 根据加锁的范围,MySQL里面的锁大致可以分成…...

axios请求类型是文件流怎么显示报错信息
axios请求类型是文件流,但是报错信息的话没法显示,在request.js文件中更改一下request拦截器代码: service.interceptors.request.use(config > { ...... , error > { console.log(error, 报错报错) // 处理请求错误 if (error.respons…...

DataX 源码改造支持Mysql 8.X
文章目录 DataX 源码改造支持Mysql 8.X问题背景克隆源代码并修改重新打包生产环境发布DataX 源码改造支持Mysql 8.X 问题背景 今天在使用DataX同步数据的时候遇到一个问题,报错如下 错误信息为:java.sql.SQLException: No suitable driver found for ["jdbc:mysql://…...
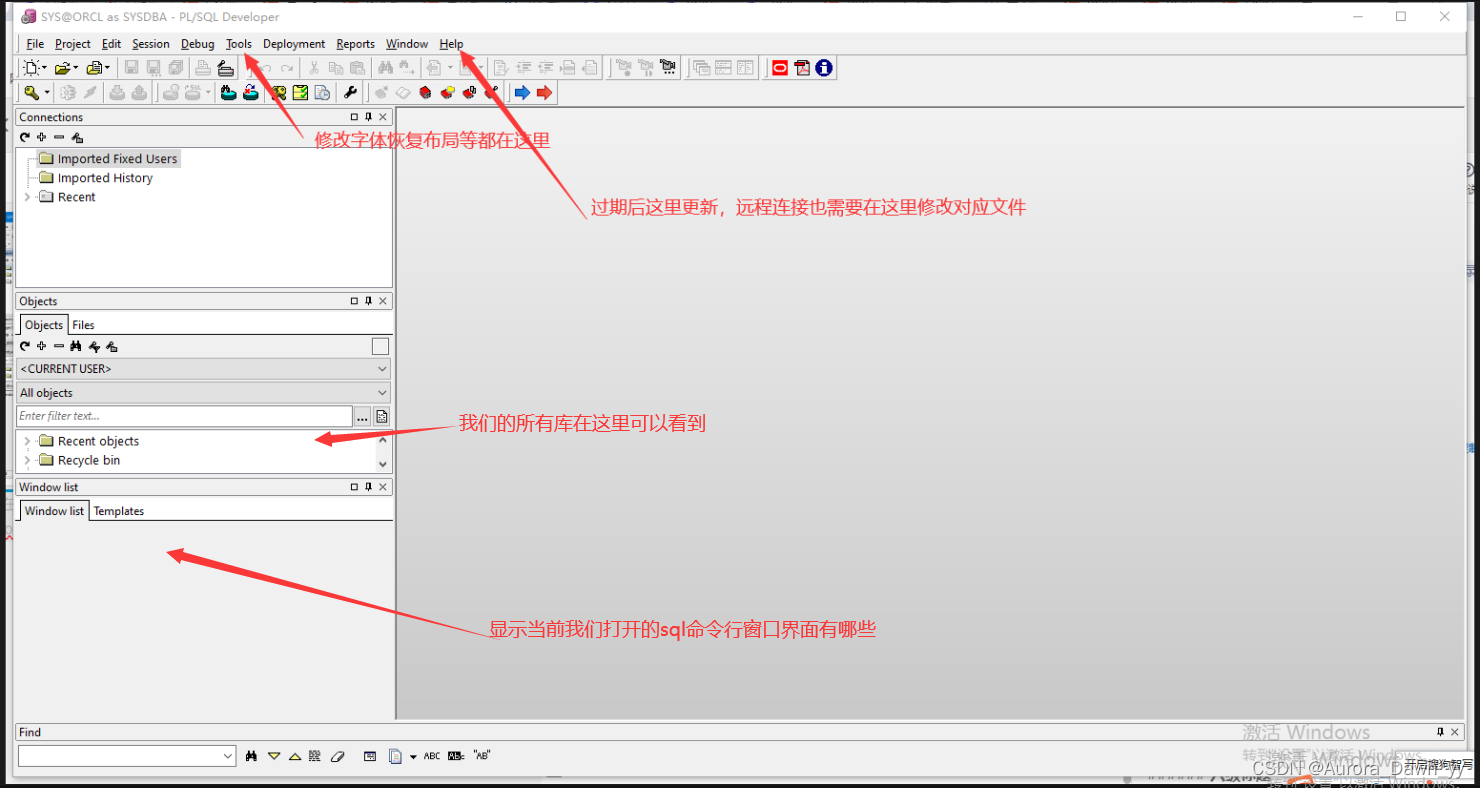
大数据学习-2024/3/29-oracle使用介绍
在plsql中登录ORACLE数据。 默认用户: 1、sys: 角色:数据库超级管理员账户。 权限:具有最高的权限,可以执行任何操作,包括操作数据字典和控制文件。可以创建和删除数据库对象,授予和回收其他用户…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...
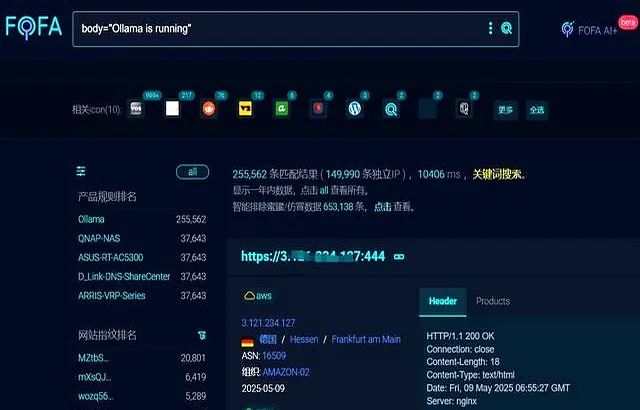
未授权访问事件频发,我们应当如何应对?
在当下,数据已成为企业和组织的核心资产,是推动业务发展、决策制定以及创新的关键驱动力。然而,未授权访问这一隐匿的安全威胁,正如同高悬的达摩克利斯之剑,时刻威胁着数据的安全,一旦触发,便可…...

云原生时代的系统设计:架构转型的战略支点
📝个人主页🌹:一ge科研小菜鸡-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、云原生的崛起:技术趋势与现实需求的交汇 随着企业业务的互联网化、全球化、智能化持续加深,传统的 I…...
MeanFlow:何凯明新作,单步去噪图像生成新SOTA
1.简介 这篇文章介绍了一种名为MeanFlow的新型生成模型框架,旨在通过单步生成过程高效地将先验分布转换为数据分布。文章的核心创新在于引入了平均速度的概念,这一概念的引入使得模型能够通过单次函数评估完成从先验分布到数据分布的转换,显…...
