数据结构·二叉树(2)
目录
1 堆的概念
2 堆的实现
2.1 堆的初始化和销毁
2.2 获取堆顶数据和堆的判空
2.3 堆的向上调整算法
2.4 堆的向下调整算法
2.4 堆的插入
2.5 删除堆顶数据
2.6 建堆
3 建堆的时间复杂度
3.1 向上建堆的时间复杂度
3.2向下建堆的时间复杂度
4 堆的排序
前言:前面介绍了树以及二叉树及其二叉树的存储方式,本文就介绍基于二叉树模式下的一种结构——堆。
1 堆的概念
堆分为大堆和小堆,小堆是指每个父节点的值都小于子节点,大堆是子节点的值都大于父节点,
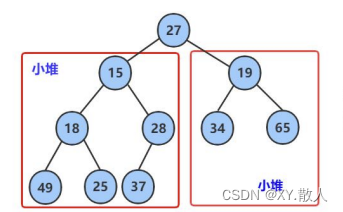
小堆是这样的,大堆同理就可以了。
堆在逻辑上是完全二叉树结构,实际的物理结构是数组,接下来就进入到重点——堆的实现。
2 堆的实现
实现堆的时候,我们不像之前实现顺序表的时候,有增删查改以及指定位置的删除增加等等,因为堆单纯用来存储数据是没有太大的意义的,所以实现的接口也不大一样。
堆同样用结构体定义,一个是数据,一个是空间大小,一个是有效数据个数。
typedef int HDataType;typedef struct Heap
{HDataType* arr;int size;int capacity;
}Heap;//堆的初始化
void HPInit(Heap* php);//建堆
void HPInitArray(Heap* php,HDataType* a, int n);//堆的销毁
void HPDestroy(Heap* php);//堆的插入
void HPPush(Heap* php,HDataType x);//获取堆顶数据
HDataType HPTop(Heap* hp);//堆的删除数据
void HPPop(Heap* php);//堆的判空
bool HPempty(Heap* php);//堆的向上调整算法
void AdjustUp(HDataType* arr,int child);//堆的向下调整算法
void AdjustDown(HDataType* arr,int size ,int parent);2.1 堆的初始化和销毁
销毁和初始化与之前线性表的初始化基本上就是一样的,不用过多介绍
void HPInit(Heap* php)
{assert(php);php->arr = NULL;php->capacity = php->size = 0;
}//堆的销毁
void HPDestroy(Heap* php)
{assert(php);free(php->arr);php->arr = NULL;php->capacity = php->size = 0;
}
2.2 获取堆顶数据和堆的判空
获取数据只需要判断堆是不是空的就行,判空只需要检查size的值就可以了。
bool HPempty(Heap* php)
{assert(php);return php->size == 0;
}//获取堆顶数据
HDataType HPTop(Heap* php)
{assert(php);assert(!HPempty(php));return php->arr[0];
}因为后面的向上调整和向下调整,我们对于数据的交换用的是很频繁的,所以我们单独创建一个函数用来交换数据:
//交换数据
void Swap(HDataType* px, HDataType* py)
{HDataType tem = *px;*px = *py;*py = tem;
}2.3 堆的向上调整算法
堆的向上调整算法,即是我们插入数据之后,保持数据的结构依然是堆,所以向上调整就是从最后一个数据入手,往上依次调整,如果堆是小堆,那么就是子节点与父节点比较大小,子节点小于父节点,就交换,大堆同理可得。
那么向上调整,我们知道子节点,如何求的父节点呢?
其实通过节点之间的存储规律,我们可以得到
左子节点 = 父节点 * 2 + 1,右子节点 = 父节点 * 2 + 2;
知道任意子节点我们就可以求父节点,实际操作的时候我们求父节点的时候怎么知道子节点是左还是右呢?
解决方法就是不管三七二十一,父节点 = (子节点 - 1) / 2,不管多出来的1,因为整型运算,1 / 2 = 0,所以1是被忽略了。
因为调整的次数可能不止一次,可能调整到高度的一半就停止了,或者是调整到了根部,所以我们使用while循环,循环条件就是子节点的下标,因为经历一次调整后,子节点会到父节点上,父节点又到该节点的父节点上,那么判断条件就应该是子节点的下标位置。
//堆的向上调整算法
void AdjustUp(HDataType* arr, int child)
{int parent = (child - 1) / 2;//注意大小堆的写法while (child){if (arr[child] < arr[parent]){Swap(&arr[child],&arr[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}2.4 堆的向下调整算法
如果说向上调整算法是从子节点入手,那么向下调整算法就是从父节点入手,父节点和子节点相互比较必然存在一个问题就是,子节点可能只能只有左节点,没有右节点,那我们还要考虑的是两个节点谁小的问题,父节点与两个子节点较小的节点比较,这里可以用到假设法解决。
传进去的参数是数组,堆的有效数据个数,父节点的下标。
这里同样用到while循环,因为是从上往下调整的,所以结束条件应该是child。
为什么是child而不是parent呢?因为调整到最后两层的时候,parent在倒数第二次就不用动了,已经调整结束了,所以向下调整比向上调整有一个明显的优势是在于最后一层不是干涉,时间复杂度会少很多很多,后面再介绍。
假设法找两个子节点中小的那个,为了防止存在越界访问,比如只有一个左孩子,但是child + 1就访问到了右孩子,就越界了,所以child + 1 < size就是为了防止越界访问的。
最后就是进行比较,交换,赋值了。
//堆的向下调整算法
void AdjustDown(HDataType* arr, int size, int parent)
{int child = parent * 2 + 1;//为什么不用child当作循环条件呢?while (child < size){//先找两个孩子中小的那个 假设法if (arr[child + 1] < arr[child] && child + 1 < size){child++;}//交换if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}2.4 堆的插入
堆的插入很简单的,就跟顺序表的插入一样的, 无非是最后要保持数据依然是堆而已,因为数据是在最后位置插入的,所以可以用向上算法进行调整,前面就是判断空间够不够,不够扩容就行,就没其他要注意的:
//堆的插入
void HPPush(Heap* php, HDataType x)
{assert(php);//判断空间是否足够if (php->capacity == php->size){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HDataType* tem = (HDataType*)realloc(php->arr, sizeof(HDataType) * newcapacity);if (tem == NULL){perror("realloc fail");return;}php->arr = tem;php->capacity = newcapacity;}php->arr[php->size++] = x;//插入后依然保持为堆AdjustUp(php->arr,php->size - 1);}2.5 删除堆顶数据
删除数据都是删除的堆顶数据,那么删除了之后我们该如何保持堆依然是大小堆呢?我们不能直接然后面的数据往前移动一位,这会让堆的数据完全乱套的,结构完全变化了。
前人是思路很是清奇的。我们不妨让第一个数据和末尾的数据进行交换,size--后,堆顶的数据就被删除了,问题是如何保持堆的结构呢?你看,向下调整这不就有大用了,从堆顶一直往下调整呗就,很清奇的这个思路,一下就删除好了。
结合这个思路,如果我们想要找最小,次小的数据是可以模拟这个思路的,后面介绍咯。
当然,没有数据肯定就不能删除了。
//堆的删除数据 删除的是堆顶数据
void HPPop(Heap* php)
{//数据删除之后依然保持为堆assert(php);assert(!HPempty(php));Swap(&php->arr[0], &php->arr[php->size - 1]);php->size--;AdjustDown(php->arr,php->size,0);
}2.6 建堆
建堆有两个方法,一个是初始化一个堆之后,进行插入数据,调整操作,还有一种就是,初始化的这个过程就进行调整数据,即创建好一个满足堆需求的数组,再拷贝上去就行。
数据给好之后,该赋值的也都要赋值,然后就是调整数据部分,我们可以选择向上调整也可以选择向下调整,至于效率,是向下调整优先的,所以向上调整一般用的是比较少的,后面介绍。
//建堆
void HPInitArray(Heap* php,HDataType* a,int n)
{assert(php);php->arr = (HDataType*)malloc(sizeof(HDataType) * n);if (php->arr == NULL){perror("malloc fail!");return;}memcpy(php->arr, a, sizeof(HDataType) * n);php->capacity = php->size = n;//向上建堆//for (int i = 0; i < n; i++)//{// AdjustUp(php->arr,i);//}//向下建堆for (int i = (php->size - 1 - 1) / 2; i >= 0; i--){AdjustDown(php->arr, php->size, i);}
}向下建堆有个要注意的点就是i = php->size - 1 - 1,这是为了防止越界访问,假设堆里面只有9个元素,传进去的i就是4,进入到向下调整之后,child = 9,可是这是size指向的位置,一访问就越界了。
3 建堆的时间复杂度
建堆无非就两种方式,向上建堆和向下建堆,两种方式看似相差不大,实际上时间复杂度是相差较大的,这里就来慢慢分析:
计算时间复杂度之前,我们不妨计算一下树的高度与节点个数之间的关系:
二叉树的节点是以二次方递增的,第一层有2^0个节点,第二层有2^1个节点……第h层有2^(h - 1)次方个节点,那么总节点个数N = 2^0 + 2^1 + 2^3 + …… + 2^(h - 1),这里使用高中的等比求和公式,可以得出,N = 2^h - 1,那么h = log(N + 1)。
3.1 向上建堆的时间复杂度
时间复杂度估算,即是估算每个节点执行多少次操作,第一层的节点,执行调整操作次数至多为0次,第二层1次,第三层2次,第四层3次,第h层 h -1 次。
总的执行次数就是该层的所有节点 * 该层节点执行的至多次数.
F( h ) = 2^0 * 0 + 2 ^ 1 * 1 + 2 ^ 2 * 2 + 2 ^ 3 * 3 + …… +2 ^ (h - 1) * (h - 1),这里利用高中的错位相减,可以得到F(h) = 2^(h - 2) + 2,那么F(N) = ( N + 1 ) * (log( N + 1) - 2) + 2。
所以向上建堆的时间复杂度就是O(N) = N * log(N)。
3.2向下建堆的时间复杂度
同3.1,向下建堆与向上建堆不一样的是向下建堆止步于倒数第二层,这就是为什么向下建堆算法优于向上建堆算法。
节点向下调整至多调整到倒数第二层,所以第一层的节点执行的次数为h - 1,第二层为h - 2,倒数第二层执行的次数为1次,所以:
F(h) = 2^0 * (h - 1) + 2 ^ 1 * (h - 2) + 2 ^ 2 * (h - 3) + …… + 2 ^ (h-1) * 1,结合高中的数学知识可以得到F(h) = 2^h - h - 3,F(N) = (N + 1) - log( N + 1) - 3.
所以向下建堆的时间复杂度就是O(N) = N - log(N)。
这样看来向下建堆的效率远高于向上建堆的效率。
4 堆的排序
堆用来存储数据意义不大,排序倒是有点意思,当我们想让一个数组变成升序,我们是大堆还是小堆呢? 一般来说,小堆就是子节点大于父节点,满足升序,但是实际操作发现哪哪儿都是坑,特别容易改变结构。
面的删除操作有着异曲同工之妙,我们实现升序就选择大堆,讲堆顶数据放在最后,size--就访问不了最大的数据,然后选出第二大的数据,再交换,再size--,再选择第三大的数据,再交换,再size--,重复操作,最后就实现了堆排。
//堆排
void HPsort(HDataType* arr, int size)
{for (int i = (size - 1 - 1); i >= 0 ; i--){AdjustDown(arr,size,i);}int end = size - 1;while (end){Swap(&arr[0], &arr[end]);AdjustDown(arr, end, 0);end--;}
}
感谢阅读!
相关文章:

数据结构·二叉树(2)
目录 1 堆的概念 2 堆的实现 2.1 堆的初始化和销毁 2.2 获取堆顶数据和堆的判空 2.3 堆的向上调整算法 2.4 堆的向下调整算法 2.4 堆的插入 2.5 删除堆顶数据 2.6 建堆 3 建堆的时间复杂度 3.1 向上建堆的时间复杂度 3.2向下建堆的时间复杂度 4 堆的排序 前言&…...

MATLAB算法实战应用案例精讲-【毕业季论文专用】人工智能视觉检测技术及其在实际应用中的挑战与前景
目录 摘要: 第一章:引言 1.1 研究背景 1.2 研究目的与意义...
Linux虚拟机环境搭建spark
Linux环境搭建Spark分为两个版本,分别是Scala版本和Python版本。 一、 安装Pyspark 本环境以 Python 环境为例。 1、下载spark 下载网址:https://archive.apache.org/dist/spark 下载安装包:根据自己环境选择合适版本,本环境…...

STL的string容器
string基本概念 string是C风格的字符串,本质上是一个类。 string 和 char* 的区别 char* 是一个指针; string是一个类,内部封装了 char* ,用来管理字符串,是一个 char* 型的容器。 特点 string内部封装了很多成员…...

半导体工艺技术
完整内容点击:【半导体工艺技术】...

acwing算法提高之图论--单源最短路的扩展应用
目录 1 介绍2 训练 1 介绍 本专题用来记录使用。。。。 2 训练 题目1:1137选择最佳线路 C代码如下, #include <iostream> #include <cstring> #include <algorithm> #include <queue>using namespace std;const int N 101…...

SQLServer数据库使用Function实现根据字段内容的拼音首字母进行数据查询
实现SQL首字母查询分两步,第一步建Function,第二步引用新建的Function。 1. 首先需要自定义一个查询的Function,详细SQL如下: ALTER function [dbo].[GetDataByPY](str nvarchar(4000)) returns nvarchar(4000) as begin decla…...
Linux——信号概念与信号产生方式
目录 一、概念 二、前台进程与后台进程 1.ctrlc 2.ctrlz 三、信号的产生方式 1.键盘输入产生信号 2.系统调用发送信号 2.1 kill()函数 2.2 raise()函数 2.3 abort()函数 3.异常导致信号产生 3.1 除0异常 3.2 段错误异常 4.软件条件产生信号 4.1 管道 4.2 闹钟…...
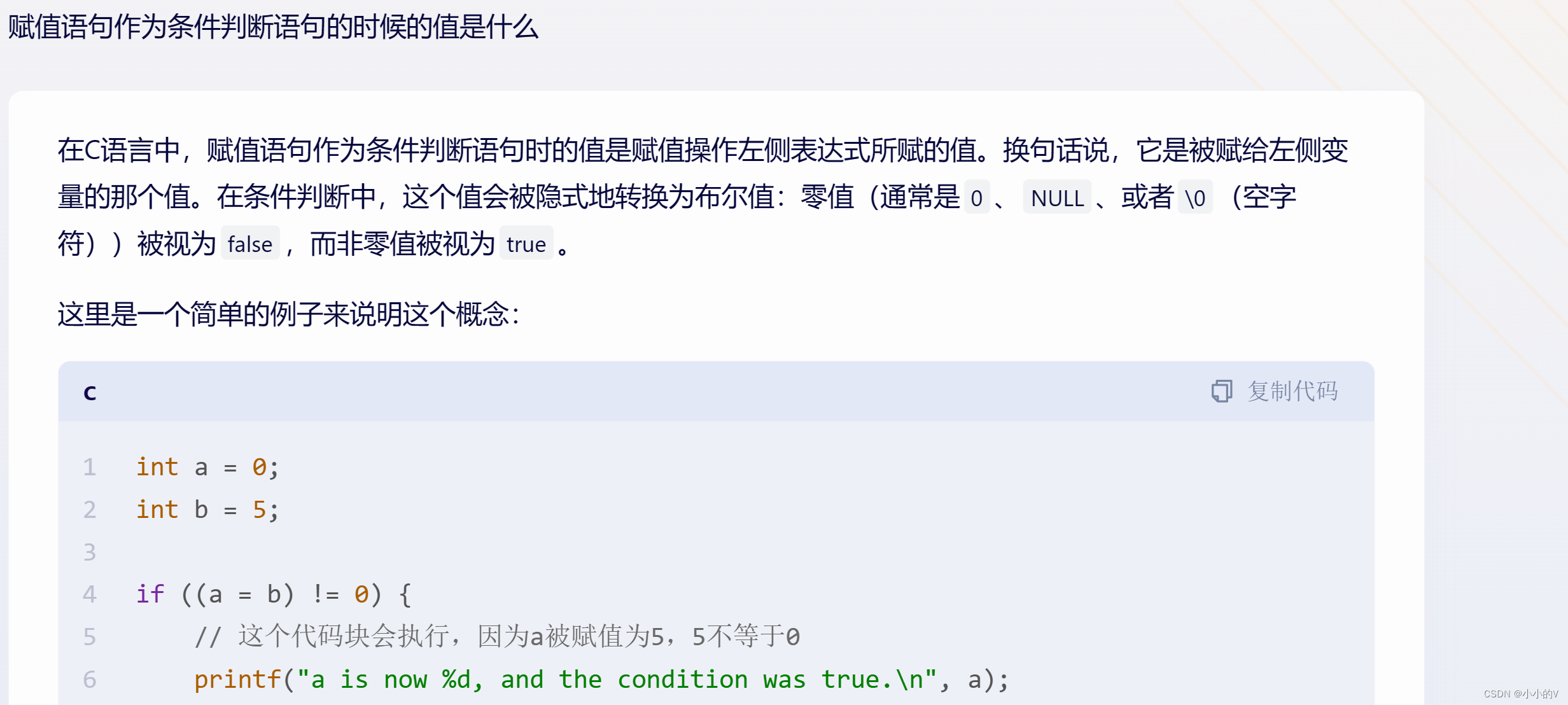
赋值语句还能当判断条件?涨芝士了!
赋值和条件看似是C语言中毫不相关的两个概念,虽然实际过程中我猜测不会有太多这种不太符合常理的情况出现,但是现在在学习的过程中,为了出题而出题总是会整出一些花活出来.....这很难不让人联想起高中时一些大佬为了彰显自己的数学天赋而自己…...
数据结构 - 算法效率|时间复杂度|空间复杂度
目录 1.算法效率 2.时间复杂度 2.1定义 2.2大O渐近表示法 2.3常见时间复杂度计算举例 3.空间复杂度 3.1定义 3.2常见空间复杂度计算举例 1.算法效率 算法的效率常用算法复杂度来衡量,算法复杂度描述了算法在输入数据规模变化时,其运行时间和空间…...
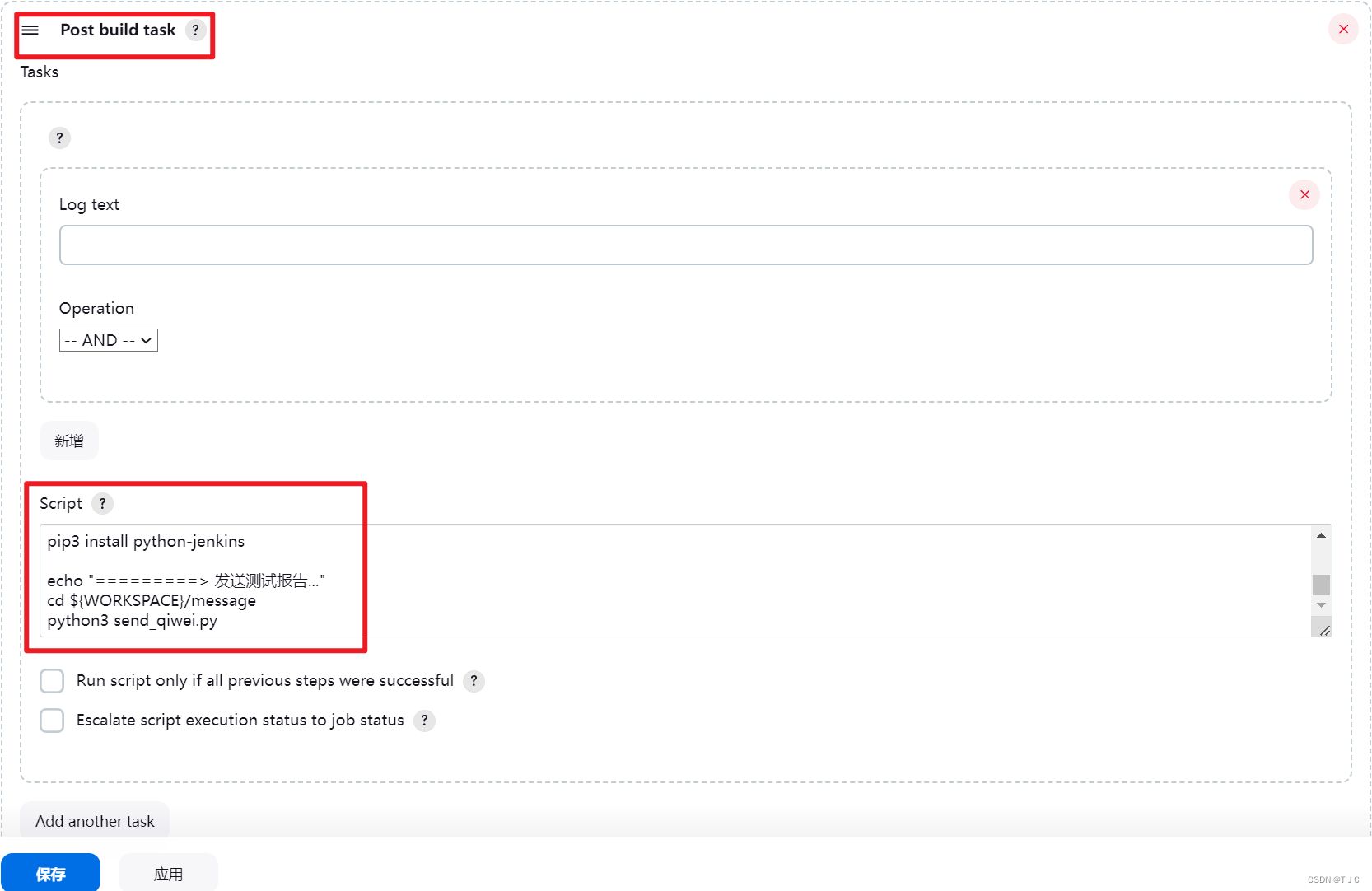
接口自动化之 + Jenkins + Allure报告生成 + 企微消息通知推送
接口自动化之 Jenkins Allure报告生成 企微消息通知推送 在jenkins上部署好项目,构建成功后,希望可以把生成的报告,以及结果统计发送至企微。 效果图: 实现如下。 1、生成allure报告 a. 首先在Jenkins插件管理中&#x…...

『Apisix安全篇』探索Apache APISIX身份认证插件:从基础到实战
🚀『Apisix系列文章』探索新一代微服务体系下的API管理新范式与最佳实践 【点击此跳转】 📣读完这篇文章里你能收获到 🛠️ 了解APISIX身份认证的重要性和基本概念,以及如何在微服务架构中实施API安全。🔑 学习如何使…...
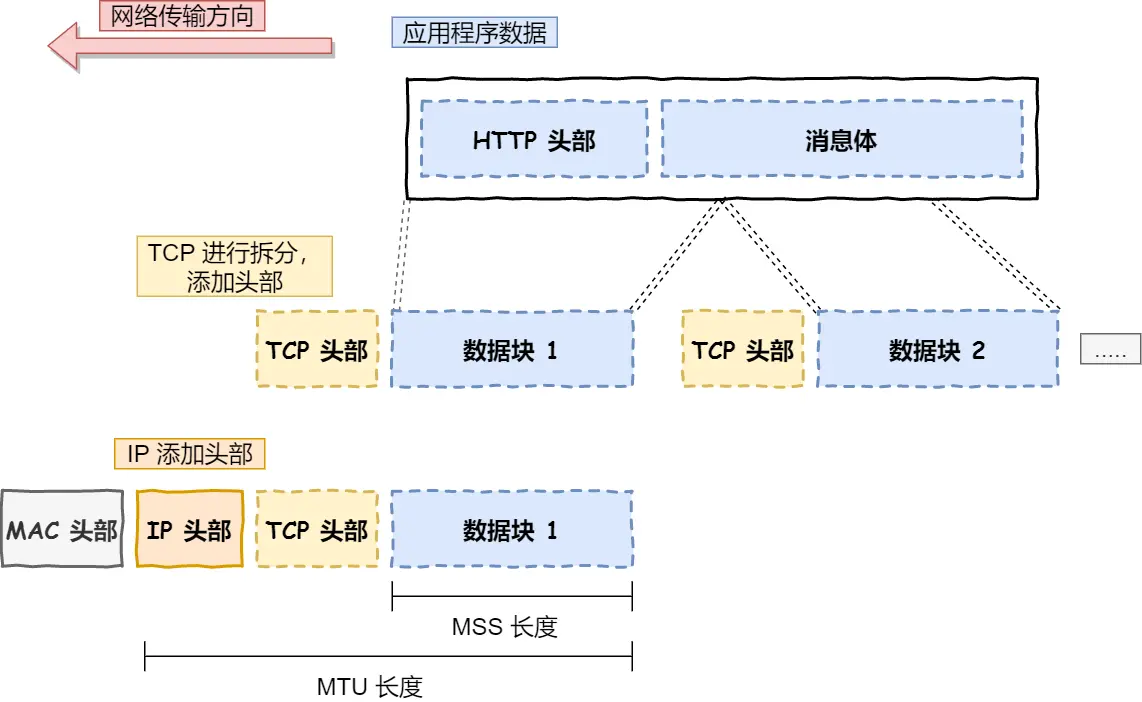
【01-20】计算机网络基础知识(非常详细)从零基础入门到精通,看完这一篇就够了
【01-20】计算机网络基础知识(非常详细)从零基础入门到精通,看完这一篇就够了 以下是本文参考的资料 欢迎大家查收原版 本版本仅作个人笔记使用1、OSI 的七层模型分别是?各自的功能是什么?2、说一下一次完整的HTTP请求…...
)
『大模型笔记』常见的分布式并行策略(分布式训练)
常见的分布式并行策略(分布式训练) 文章目录 一. 为什么分布式训练越来越流行二. 常见的并行策略2.1 数据并行2.2 模型并行2.3 流水并行2.4 混合并行二. 参考文献一. 为什么分布式训练越来越流行 近年来,深度学习被广泛应用到各个领域,包括计算机视觉、语言理解、语音识别、广…...
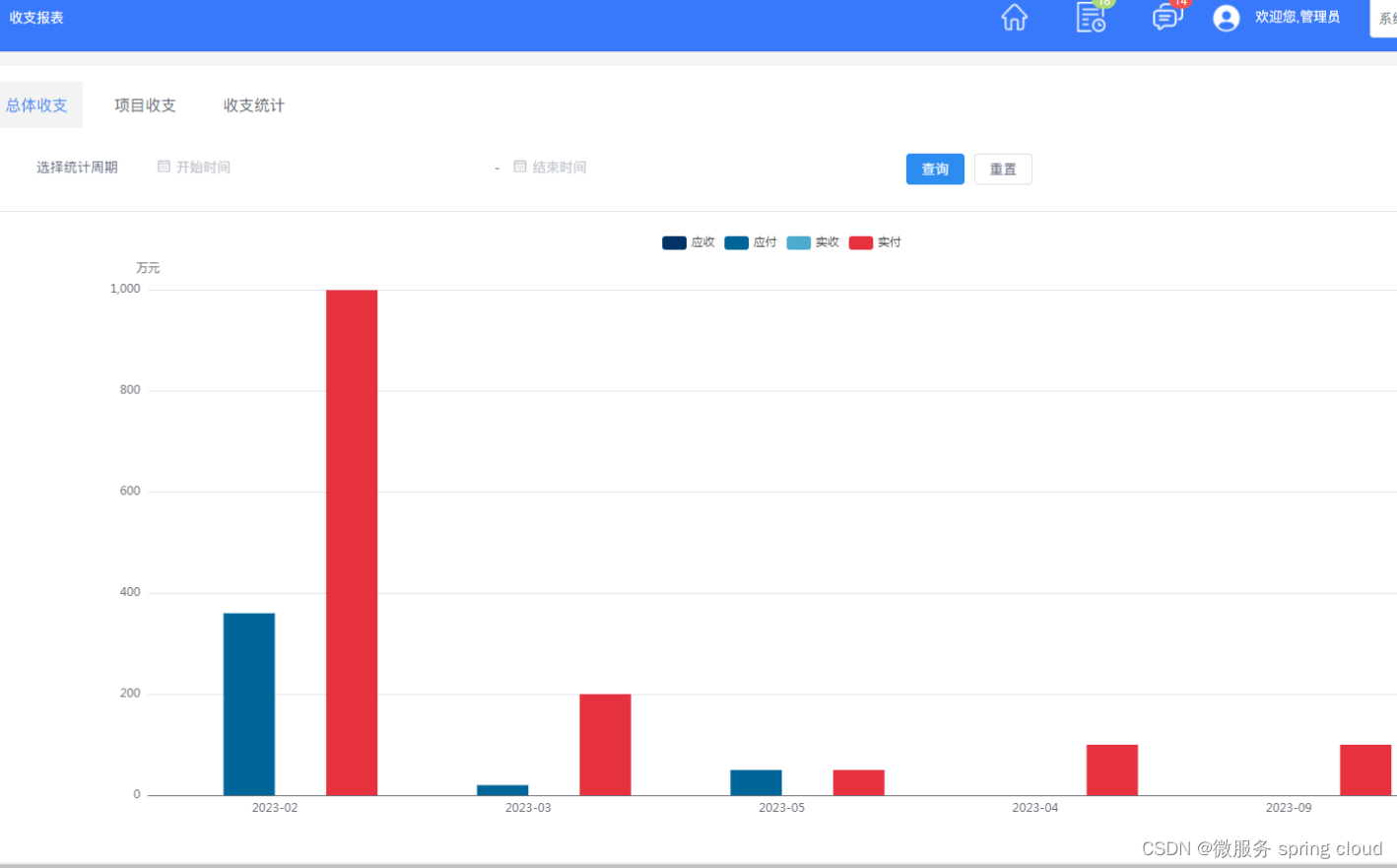
java 企业工程管理系统软件源码+Spring Cloud + Spring Boot +二次开发+ 可定制化
工程项目管理软件是现代项目管理中不可或缺的工具,它能够帮助项目团队更高效地组织和协调工作。本文将介绍一款功能强大的工程项目管理软件,该软件采用先进的Vue、Uniapp、Layui等技术框架,涵盖了项目策划决策、规划设计、施工建设到竣工交付…...
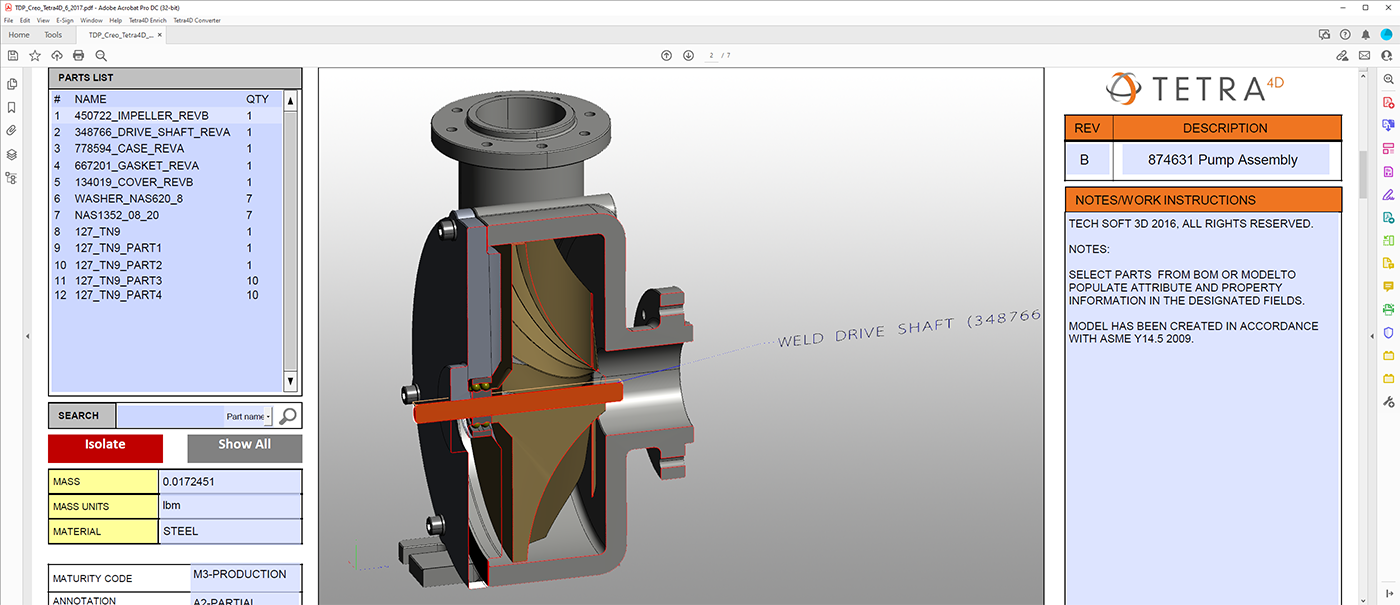
3D数据格式导出工具HOOPS Publish如何生成高质量3D PDF?
在当今数字化时代,从建筑设计到制造业,从医学领域到电子游戏开发,3D技术已经成为了不可或缺的一部分。在这个进程中,将3D模型导出为3D PDF格式具有重要的意义。同时,HOOPS Publish作为一个领先的解决方案,为…...

【springboot】闲话 springboot 的几种异步机制 及 长轮询的概念和简单实现
文章目录 引子springboot的几种异步形式开启异步支持和线程池配置(重要)第一种:Async第二种:Callable<T>第三种:WebAsyncTask<T>第四种:DeferredResult<T> 长轮询的简单实现概念实现服务…...

Mysql---安全值守常用语句
文章目录 目录 文章目录 一.用户权限设置 用户设置 元数据查询 Union联合查询 分组查询 字符串函数 总结 一.用户权限设置 用户设置 #用户创建 create user "用户名""%主机名" identified by "密码" #用户删除 drop user 用户名 #用户查询…...

containerd快速安装指南
1 containerd快速安装指南🚀 本指南旨在提供一个简洁有效的方法来安装containerd。我们将通过一份易于理解的脚本步骤,指导您完成安装🔧。请根据您的实际需求,适当调整containerd版本及其相关依赖。 注意事项: 本安装…...

Javascript - 正则表达式相关的一些基础的范例
很久以前的一些学习资料,归档发布; 正则表达式的基础,以HTML代码来示范: <html><head><title></title><script language"javascript">function test(){//从页面要求客户输入一个字符串…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
