算法学习——LeetCode力扣动态规划篇10(583. 两个字符串的删除操作、72. 编辑距离、647. 回文子串、516. 最长回文子序列)
算法学习——LeetCode力扣动态规划篇10

583. 两个字符串的删除操作
583. 两个字符串的删除操作 - 力扣(LeetCode)
描述
给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。
每步 可以删除任意一个字符串中的一个字符。
示例
示例 1:
输入: word1 = “sea”, word2 = “eat”
输出: 2
解释: 第一步将 “sea” 变为 “ea” ,第二步将 "eat "变为 “ea”
示例 2:
输入:word1 = “leetcode”, word2 = “etco”
输出:4
提示
1 <= word1.length, word2.length <= 500
word1 和 word2 只包含小写英文字母
代码解析
动态规划
和1143相同,只要求出两个字符串的最长公共子序列长度即可,那么除了最长公共子序列之外的字符都是必须删除的,最后用两个字符串的总长度减去两个最长公共子序列的长度就是删除的最少步数。
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size()+1 , vector<int>(word2.size()+1 ,0));for(int i=0 ;i<word1.size() ;i++){for(int j=0 ;j<word2.size() ;j++){if(word1[i] == word2[j]) dp[i+1][j+1] = dp[i][j] + 1;else dp[i+1][j+1] = max(dp[i][j+1],dp[i+1][j]);}}return word1.size() + word2.size() - 2*dp[word1.size()][word2.size()];}
};
72. 编辑距离
72. 编辑距离 - 力扣(LeetCode)
描述
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例
示例 1:
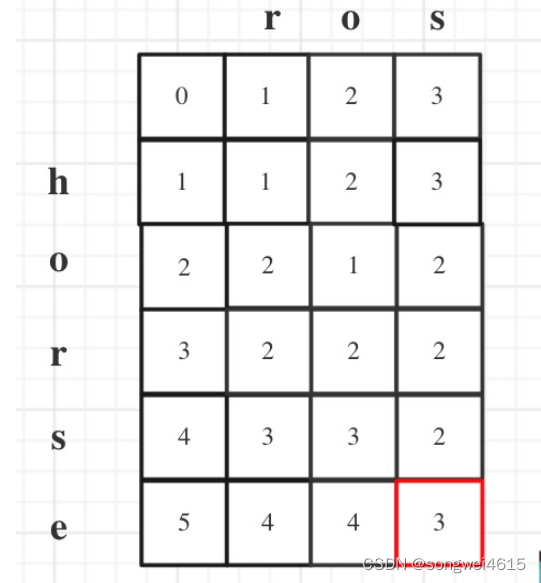
输入:word1 = “horse”, word2 = “ros”
输出:3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
示例 2:
输入:word1 = “intention”, word2 = “execution”
输出:5
解释:
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)
提示
0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成
代码解析
动态规划
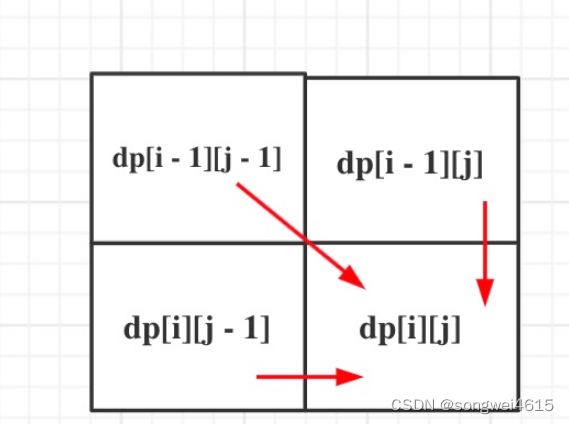
- 确定dp数组以及下标的含义
dp[i][j] 表示前 i 个字符的word1,和前 j 个字符的word2,最近编辑距离。 - 递推公式
- if (word1[ i ] == word2[ j ]) 那么说明不用任何编辑,
即dp[i+1][j+1] = dp[i ][j ]; - if (word1[ i ] != word2[ j ]) 有三种情况
- 删除world1
word1第 i 个字符删除一个元素,就是world1第 i -1 与world2第 j 再加上一个操作。
即 dp[i+1][j+1] = dp[ i ][ j+1] + 1; - 删除world2(相当于添加world1)
word2第 j 个字符删除一个元素,就是world1第 i 与world2第 j -1 再加上一个操作。
即 dp[i+1][j+1] = dp[ i +1][ j] + 1; - 替换元素
word1第 i 个字符和word1第 i -1个字符替换,world2同样,就是world1第 i -1 与world2第 j -1 再加上一个操作。
即 dp[i+1][j+1] = dp[ i ][ j] + 1; - 最终三种情况取最小
dp[i+1][j+1] = min( dp[i][j] , min(dp[i][j+1],dp[i+1][j])) + 1;
- 删除world1
- if (word1[ i ] == word2[ j ]) 那么说明不用任何编辑,
- dp数组初始化
-
dp[i][0] :以下标i-1为结尾的字符串word1,和空字符串word2,最近编辑距离为dp[i][0]。
那么dp[i][0]就应该是i,对word1里的元素全部做删除操作,即:dp[i][0] = i; -
同理dp[0][j] = j;
-
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size()+1 , vector<int>(word2.size()+1));for(int i=0 ; i<word1.size();i++)dp[i+1][0] = i+1;for(int j=0 ; j<word2.size();j++)dp[0][j+1] = j+1;for(int i=0;i<word1.size();i++){for(int j=0; j<word2.size();j++){if(word1[i] == word2[j]) dp[i+1][j+1] = dp[i][j];else dp[i+1][j+1] = min( dp[i][j] , min(dp[i][j+1],dp[i+1][j])) + 1;}}return dp[word1.size()][word2.size()];}
};
647. 回文子串
647. 回文子串 - 力扣(LeetCode)
描述
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例
示例 1:
输入:s = “abc”
输出:3
解释:三个回文子串: “a”, “b”, “c”
示例 2:
输入:s = “aaa”
输出:6
解释:6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”
提示
1 <= s.length <= 1000
s 由小写英文字母组成
代码解析
暴力法
class Solution {
public:bool cheak(const string s , int left,int right){for(int i=left ,j=right; i<=(right-left)/2 +left; i++,j--){if(s[i]!=s[j]) return false;}return true;}int countSubstrings(string s) {if(s.size()<=1) return 1;int num=0;int left=0,right=1;for(int left=0 ; left<s.size() ;left++){for(right=left ; right<s.size();right++){if(cheak(s,left,right)==1){num++;// cout<<left<<' '<<right<<endl;}}}return num;}
};动态规划
-
确定dp数组(dp table)以及下标的含义
布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。 -
确定递推公式
在确定递推公式时,就要分析如下几种情况。-
当s[i]与s[j]不相等,那没啥好说的了,dp[i][j]一定是false。
-
当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况
情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
情况二:下标i 与 j相差为1,例如aa,也是回文子串
情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
-
-
dp数组如何初始化
dp[i][j]可以初始化为true么? 当然不行,怎能刚开始就全都匹配上了。
所以dp[i][j]初始化为false。 -
确定遍历顺序
遍历顺序可有有点讲究了。
首先从递推公式中可以看出,情况三是根据dp[i + 1][j - 1]是否为true,在对dp[i][j]进行赋值true的。
dp[i + 1][j - 1] 在 dp[i][j]的左下角,
一定要从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的。
因为dp[i][j]的定义,所以j一定是大于等于i的,那么在填充dp[i][j]的时候一定是只填充右上半部分。

class Solution {
public:int countSubstrings(string s) {if(s.size()<=1) return 1;vector<vector<bool>> dp(s.size(),vector<bool>(s.size() , false));int num = 0;for(int i=s.size()-1 ; i>=0;i--)for(int j=i ;j<s.size();j++)//s[i]==s[j]为首尾相同//并且j-i <= 1为"a"或者"aa"的情况,为回文串//如果j-i不是<=1,但是dp[i+1][j-1]==true,也是回文串,因为首位相同中间是回文串//如dabcd,首位d相同,中间dp[i+1][j-1]为abc也是回文串,即dabcd为回文串if( s[i]==s[j] &&(j-i <= 1||dp[i+1][j-1]==true) ) {num++;dp[i][j] = true;}return num;}
};
516. 最长回文子序列
516. 最长回文子序列 - 力扣(LeetCode)
描述
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
示例
示例 1:
输入:s = “bbbab”
输出:4
解释:一个可能的最长回文子序列为 “bbbb” 。
示例 2:
输入:s = “cbbd”
输出:2
解释:一个可能的最长回文子序列为 “bb” 。
提示
1 <= s.length <= 1000
s 仅由小写英文字母组成
代码解析
动态规划
-
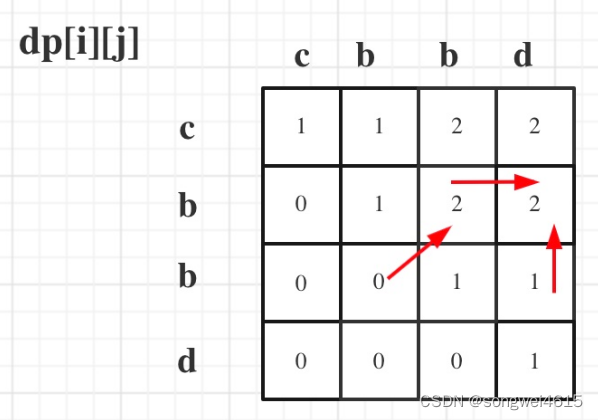
确定dp数组(dp table)以及下标的含义
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。 -
确定递推公式
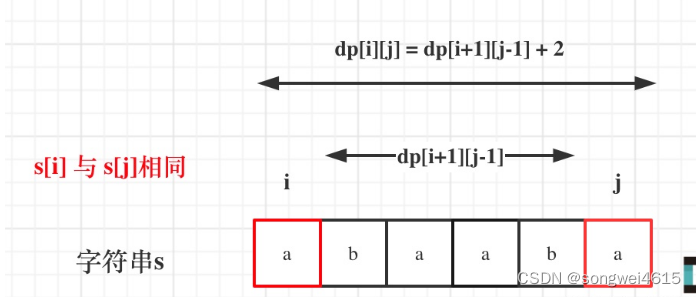
在判断回文子串的题目中,关键逻辑就是看s[i]与s[j]是否相同。- 如果s[i]与s[j]相同,
- j - i ==0 , dp[i][j] = 1;
- j - i == 1, dp[i][j] = 2;
- j - i > 2, dp[i][j] = dp[i + 1][j - 1] + 2;
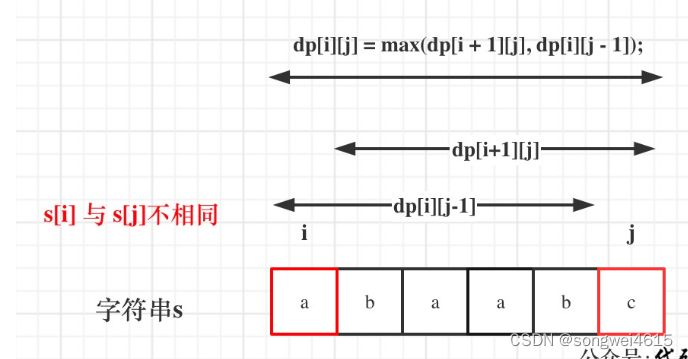
- 如果s[i]与s[j]不同
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
- 如果s[i]与s[j]相同,
- 确定遍历顺序
从递推公式dp[i][j] = dp[i + 1][j - 1] + 2 和 dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]) 可以看出,dp[i][j]是依赖于dp[i + 1][j - 1] 和 dp[i + 1][j],
也就是从矩阵的角度来说,dp[i][j] 下一行的数据。 所以遍历i的时候一定要从下到上遍历,这样才能保证,下一行的数据是经过计算的。
class Solution {
public:int longestPalindromeSubseq(string s) {if(s.size()<=1) return s.size();vector<vector<int>> dp(s.size() , vector<int>(s.size() ,0));int result = 0;for(int i=s.size()-1; i>=0 ;i-- )for(int j=i ;j<s.size();j++){if(s[i]==s[j]){if(j==i) dp[i][j] = 1;else if(j-i==1) dp[i][j] = 2;else dp[i][j] = dp[i+1][j-1] + 2;if(dp[i][j] > result) result = dp[i][j];}else{dp[i][j] = max(dp[i][j-1],dp[i+1][j]);}}// for(int i=0;i<s.size();i++)// {// for(int j=0;j<s.size();j++)// cout<<dp[i][j]<<' ';// cout<<endl;// }return result;}
};
相关文章:

算法学习——LeetCode力扣动态规划篇10(583. 两个字符串的删除操作、72. 编辑距离、647. 回文子串、516. 最长回文子序列)
算法学习——LeetCode力扣动态规划篇10 583. 两个字符串的删除操作 583. 两个字符串的删除操作 - 力扣(LeetCode) 描述 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个…...
TASKPROMPTER
baseline模型的预训练权重就有1.6G! 多吓人呐,当时我就暂停下载了,不建议复现...

C之易错注意点转义字符,sizeof,scanf,printf
目录 前言 一:转义字符 1.转义字符顾名思义就是转换原来意思的字符 2.常见的转义字符 1.特殊\b 2. 特殊\ddd和\xdd 3.转义字符常错点----计算字符串长度 注意 : 如果出现\890,\921这些的不是属于\ddd类型的,,不是一个字符…...
)
等级保护测评无补偿因素的高风险安全问题判例(共23项需整改)
层面 控制点 要求项 安全问题 适用范围 充分条件 整改建议简要 安全物理环境 基础设施位置 应保证云计算基础设施位于中国境内 1.云计算基础设施物理位置不当 二级及以上 相关基础设施不在中国境内 云平台相关基础设施在中国境内部署 安全通信网络 网络架构 应…...

JavaScript笔记 09
目录 01 DOM操作事件的体验 02 获取元素对象的五种方式 03 事件中this指向问题 04循环绑定事件 05 DOM节点对象的常用操作 06 点亮盒子的案例 07 节点访问关系 08 设置和获取节点内容的属性 09 以上内容的小总结 01 DOM操作事件的体验 js本身是受事件驱动的脚本语言 什…...

操作教程|在MeterSphere中通过SSH登录服务器的两种方法
MeterSphere开源持续测试平台拥有非常强大的插件集成机制,用户可以通过插件实现平台能力的拓展,借助插件或脚本实现多种功能。在测试过程中,测试人员有时需要通过SSH协议登录至服务器,以获取某些配置文件和日志文件,或…...

Swashbuckle.AspNetCore介绍
使用 ASP.NET Core 构建的 API 的 Swagger 工具。直接从您的路由、控制器和模型生成精美的 API 文档,包括用于探索和测试操作的 UI。 除了 Swagger 2.0 和 OpenAPI 3.0 生成器外,Swashbuckle 还提供了由生成的 Swagger JSON 提供支持的令人敬畏的 swagg…...

【Spring】通过Spring收集自定义注解标识的方法
文章目录 前言1. 声明注解2. 使用 Spring 的工厂拓展3. 收集策略4. 完整的代码后记 前言 需求: 用key找到对应的方法实现。使用注解的形式增量开发。 MyComponent public class Sample1 {MyMethod(key "key1")public String test2() {return "She…...

基于深度学习的图书管理推荐系统(python版)
基于深度学习的图书管理推荐系统 1、效果图 1/1 [] - 0s 270ms/step [13 11 4 19 16 18 8 6 9 0] [0.1780757 0.17474999 0.17390694 0.17207369 0.17157653 0.168248440.1668652 0.16665359 0.16656876 0.16519257] keras_recommended_book_ids深度学习推荐列表 [9137…...

MATLAB 点云随机渲染赋色(51)
MATLAB 点云随机渲染赋色(51) 一、算法介绍二、算法实现1.代码2.效果总结一、算法介绍 为点云中的每个点随机赋予一种颜色,步骤和效果如图: 1、读取点云 (ply格式) 2、随机为每个点的RGB颜色字段赋值 3、保存结果 (ply格式) 二、算法实现 1.代码 代码如下(示例):…...

通过一篇文章让你完全掌握VS和电脑常用快捷键的使用方法
VS常用快捷键 前言一、 VS常用快捷键常用VS运行调试程序快捷键常用VS编辑程序快捷键 二、常用windows系统操作快捷键 前言 VS(Visual Studio)是一款强大的开发工具,提供了许多常用快捷键,以提高开发效率。这些快捷键包括文件操作…...

ChatGPT指引:借助ChatGPT撰写学术论文的技巧
ChatGPT无限次数:点击直达 ChatGPT指引:借助ChatGPT撰写学术论文的技巧 在当今信息技术高度发达的时代,人工智能技术的不断发展为学术研究者提供了更多的便利和可能。其中,自然语言处理技术中的ChatGPT无疑是一种强大的工具,它能…...
魔改一个过游戏保护的CE
csdn审核不通过 网易云课堂有配套的免费视频 int0x3 - 主页 文章都传到github了 Notes/外挂/魔改CE at master MrXiao7/Notes GitHub 为什么要编译自己的CE 在游戏逆向的过程中,很多游戏有保护,我们运行原版CE的时候会被检测到 比如我们开着CE运…...

rust嵌入式开发之await
嵌入式经常有类似通过串口发送指令然后等待响应再做出进一步反应的需求。比如,通过串口以AT命令来操作蓝牙模块执行扫描、连接,需要根据实际情况进行操作,复杂的可能需要执行7、8条指令才能完成连接。 对于这样的需求,如果用异步…...

UE4_碰撞_碰撞蓝图节点——Line Trace For Objects(对象的线条检测)
一、Line Trace For Objects(对象的线条检测):沿给定线条执行碰撞检测并返回遭遇的首个命中,这只会找到由Object types指定类型的对象。注意他与Line Trace By Channel(由通道检测线条)的区别,一个通过Obje…...
抽象类和接口的简单认识
目录 一、抽象类 1.什么是抽象类 2.抽象类的注意事项 3.抽象类与普通类的对比 二、接口 1.接口的简单使用 2.接口的特性 3.接口的使用案例 4.接口和抽象类的异同 一、抽象类 所谓抽象类,就是更加抽象的类,也就是说,这个类不能具体描…...
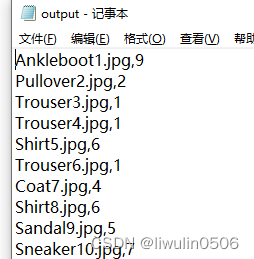
python-pytorch获取FashionMNIST实际图片标签数据集
在查看pytorch官方文档的时候,在这里链接中https://pytorch.org/tutorials/beginner/basics/data_tutorial.html的Creating a Custom Dataset for your files章节,有提到要自定义数据集,需要用到实际的图片和标签。 在网上找了半天没找到&a…...

深入探秘Python生成器:揭开神秘的面纱
一、问题起源: 想象一下,您掌握了一种魔法,在代码世界里,您可以轻松呼唤出一个整数。然而,事情并不总是看起来那样简单。在Python的奇妙王国中,我遇到了一个有趣的谜题: def tst():try:print(…...

红队攻防渗透技术实战流程:红队目标信息收集之批量信息收集
红队资产信息收集 1. 自动化信息收集1.1 自动化信息收集工具1.2 自动域名转换IP工具1.3 自动企业信息查询工具1.4 APP敏感信息扫描工具1.5 自动化信息工具的使用1.5.1 资产灯塔系统(ARL)1.5.1.1 docker环境安装1.2.2.9.1 水泽-信息收集自动化工具1. 自动化信息收集 1.1 自动化…...
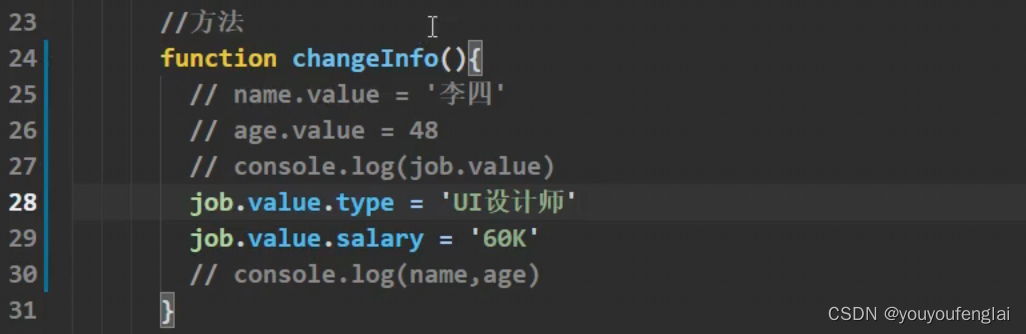
【vue3学习笔记(二)】(第141-143节)初识setup;ref函数_处理基本类型;ref函数_处理对象类型
尚硅谷Vue2.0Vue3.0全套教程丨vuejs从入门到精通 本篇内容对应课程第141-143节 课程 P141节 《初识setup》笔记 1、setup是所有组合式API“表演的舞台”,组件中所用到的所有数据、方法、监视数据、生命周期钩子等都需要配置在setup中。 2、setup的两种返回值&…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...
