【C++庖丁解牛】自平衡二叉搜索树--AVL树


目录
- 前言
- 1 AVL树的概念
- 2. AVL树节点的定义
- 3. AVL树的插入
- 4. AVL树的旋转
- 实现代码
- 5 AVL树的验证
- 6 AVL树的删除(了解)
- 7 AVL树的性能
前言
前面对map/multimap/set/multiset进行了简单的介绍,在其文档介绍中发现,这几个容器有个共同点是:其底层都是按照二叉搜索树来实现的,但是二叉搜索树有其自身的缺陷,假如往树中插入的元素有序或者接近有序,二叉搜索树就会退化成单支树,时间复杂度会退化成O(N),因此map、set等关联式容器的底层结构是对二叉树进行了平衡处理,即采用平衡树来实现。
1 AVL树的概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
- 平衡因子 = 右子树高度 - 左子树高度
平衡因子并不是必须的,它只是一种控制方式,帮助我们更便捷的控制树
【扩充】
这里为什么高度差为1?如果高度相等不是更平衡吗?
节点是一个一个插入的,有些情况是无法做到相等的,最优就是高度差是1;比如:两个节点的树和四个节点的树等等。
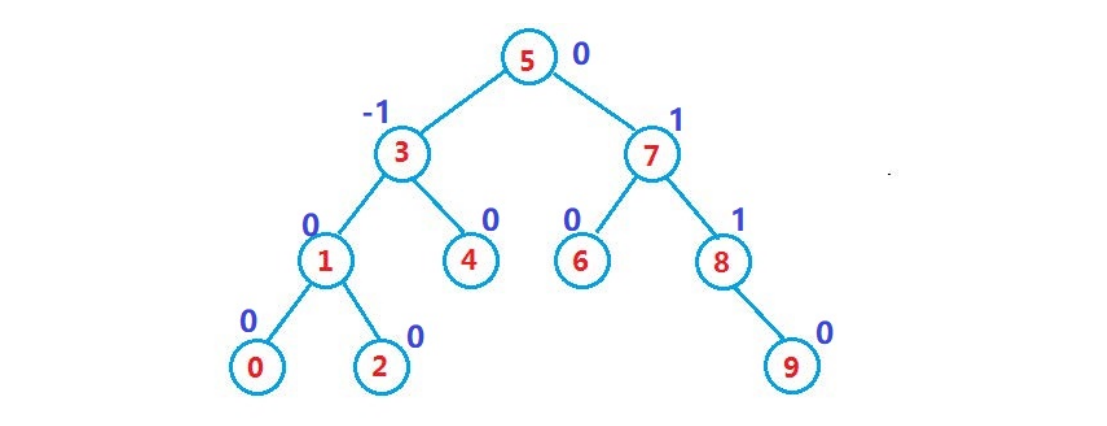
2. AVL树节点的定义
AVL树节点的定义:
template<class T>
struct AVLTreeNode
{AVLTreeNode(const T& data): _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr), _data(data), _bf(0){}AVLTreeNode<T>* _pLeft; // 该节点的左孩子AVLTreeNode<T>* _pRight; // 该节点的右孩子AVLTreeNode<T>* _pParent; // 该节点的双亲T _data;int _bf; // 该节点的平衡因子
};
3. AVL树的插入
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步:
- 按照二叉搜索树的方式插入新节点
- 调整节点的平衡因子
插入节点会影响新增节点的部分祖先
更新原则:
- 若是插入的是左节点则父节点的平衡因子减1
- 若是插入的是右节点则父节点的平衡因子加1
是否要继续更新取决于新增节点会不会影响父节点的高度,从而决定会不会影响爷爷节点
- 更新后,父节点所在的子树高度不变则不会影响爷爷节点
说明父节点的平衡因子是1或者-1,父节点在矮的那边插入了节点,左右均衡了,于是父节点的高度不变,则不会影响到爷爷,更新结束
- 更新后,父节点所在的子树高度改变则会影响爷爷节点
说明更新前,父节点的平衡因子是0,父节点变得不均衡,但是不违反规则,高度改变,会影响爷爷节点继续往上更新
更新后,父节点的平衡因子为2或-2,说明该子树违反了平衡规则,需要处理->旋转
代码实现:
bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//新节点插入后,AVL树的平衡性可能会遭到破坏,此时就需要更新平衡因子,并检测是否破坏了AVL树的平衡性/*pCur插入后,pParent的平衡因子一定需要调整,在插入之前,pParent的平衡因子分为三种情况:-1,0, 1, 分以下两种情况:1. 如果pCur插入到pParent的左侧,只需给pParent的平衡因子-1即可2. 如果pCur插入到pParent的右侧,只需给pParent的平衡因子+1即可此时:pParent的平衡因子可能有三种情况:0,正负1, 正负21. 如果pParent的平衡因子为0,说明插入之前pParent的平衡因子为正负1,插入后被调整成0,此时满足AVL树的性质,插入成功2. 如果pParent的平衡因子为正负1,说明插入前pParent的平衡因子一定为0,插入后被更新成正负1,此时以pParent为根的树的高度增加,需要继续向上更新3. 如果pParent的平衡因子为正负2,则pParent的平衡因子违反平衡树的性质,需要对其进行旋转处理*/while (parent){// 更新双亲的平衡因子if (cur == parent->left){parent->_bf--;}else{parent->_bf++;}// 更新后检测双亲的平衡因子if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){// 插入前双亲的平衡因子是0,插入后双亲的平衡因为为1 或者 -1 ,说明以双亲为根的二叉树的高度增加了一层,因此需要继续向上调整cur = cur->_parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 双亲的平衡因子为正负2,违反了AVL树的平衡性,需要对以pParent为根的树进行旋转处理if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else{RotateRL(parent);}break;}else{// 插入之前AVL树就有问题assert(false);}}return true;}
4. AVL树的旋转
如果在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,
使之平衡化。根据节点插入位置的不同,AVL树的旋转分为四种:
- 新节点插入较高左子树的左侧—左左:右单旋
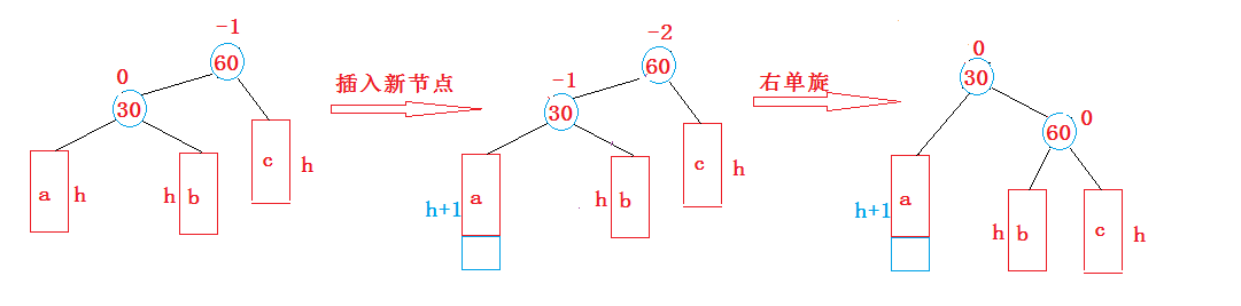
上图在插入前,AVL树是平衡的,新节点插入到30的左子树(注意:此处不是左孩子)中,30左子树增加了一层,导致以60为根的二叉树不平衡,要让60平衡,只能将60左子树的高度减少一层,右子树增加一层,即将左子树往上提,这样60转下来,因为60比30大,只能将其放在30的右子树,而如果30有右子树,右子树根的值一定大于30,小于60,只能将其放在60的左子树,旋转完成后,更新节点的平衡因子即可。
在旋转过程中,有以下几种情况需要考虑:
- 30节点的右孩子可能存在,也可能不存在
- 60可能是根节点,也可能是子树
- 如果是根节点,旋转完成后,要更新根节点
- 如果是子树,可能是某个节点的左子树,也可能是右子树
void _RotateR(PNode pParent)
{// pSubL: pParent的左孩子// pSubLR: pParent左孩子的右孩子PNode pSubL = pParent->_pLeft;PNode pSubLR = pSubL->_pRight;// 旋转完成之后,30的右孩子作为双亲的左孩子pParent->_pLeft = pSubLR;// 如果30的左孩子的右孩子存在,更新亲双亲if (pSubLR)pSubLR->_pParent = pParent;// 60 作为 30的右孩子pSubL->_pRight = pParent;// 因为60可能是棵子树,因此在更新其双亲前必须先保存60的双亲PNode pPParent = pParent->_pParent;// 更新60的双亲pParent->_pParent = pSubL;// 更新30的双亲pSubL->_pParent = pPParent;// 如果60是根节点,根新指向根节点的指针if (NULL == pPParent){_pRoot = pSubL;pSubL->_pParent = NULL;}else{// 如果60是子树,可能是其双亲的左子树,也可能是右子树if (pPParent->_pLeft == pParent)pPParent->_pLeft = pSubL;elsepPParent->_pRight = pSubL;}// 根据调整后的结构更新部分节点的平衡因子pParent->_bf = pSubL->_bf = 0;
}
-
新节点插入较高右子树的右侧—右右:左单旋
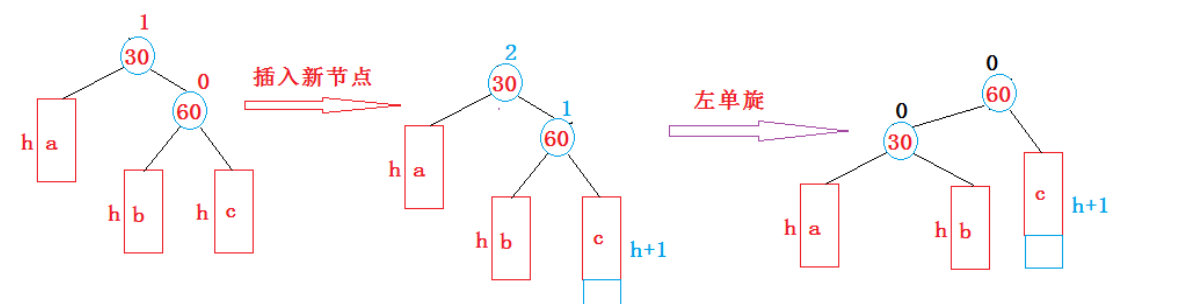
实现及情况考虑可参考右单旋。 -
新节点插入较高左子树的右侧—左右:先左单旋再右单旋
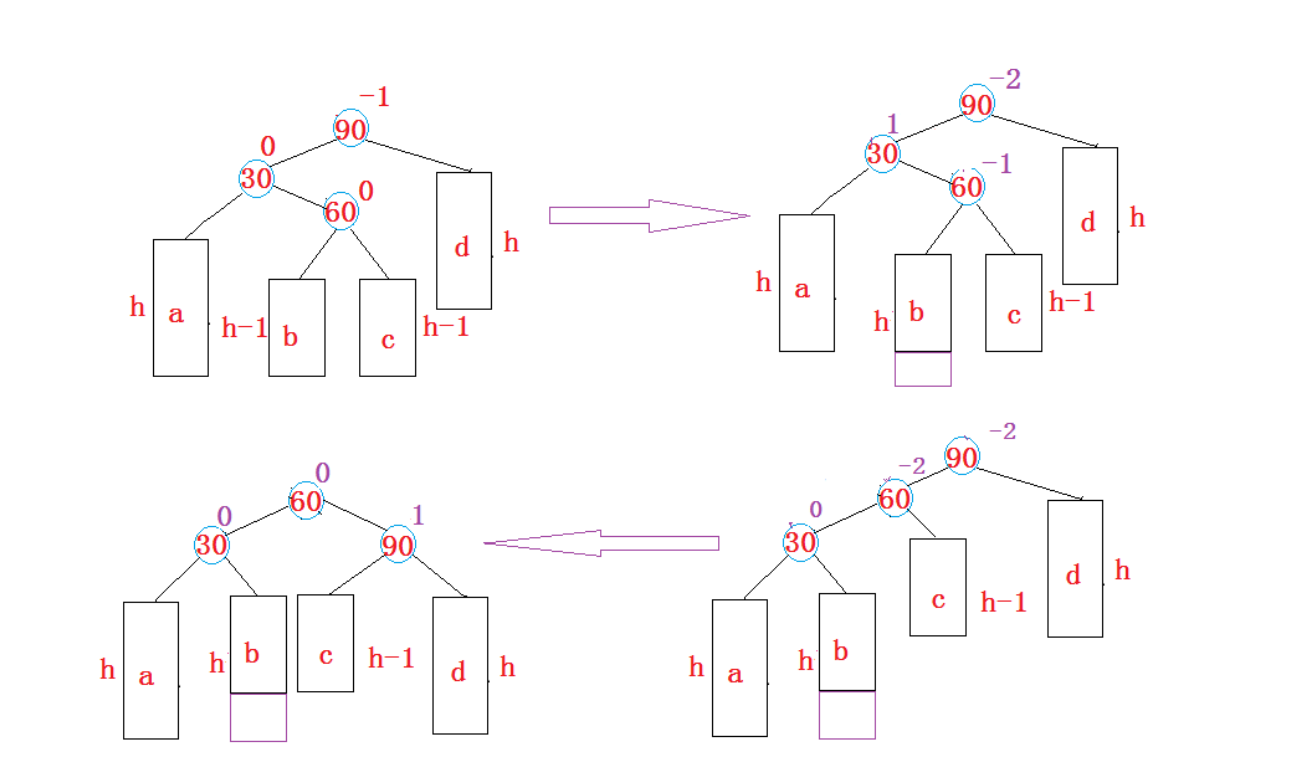
将双旋变成单旋后再旋转,即:先对30进行左单旋,然后再对90进行右单旋,旋转完成后再考虑平衡因子的更新。
// 旋转之前,60的平衡因子可能是-1/0/1,旋转完成之后,根据情况对其他节点的平衡因子进行调整
void _RotateLR(PNode pParent)
{PNode pSubL = pParent->_pLeft;PNode pSubLR = pSubL->_pRight;// 旋转之前,保存pSubLR的平衡因子,旋转完成之后,需要根据该平衡因子来调整其他节点的平衡因子int bf = pSubLR->_bf;// 先对30进行左单旋_RotateL(pParent->_pLeft);// 再对90进行右单旋_RotateR(pParent);if(1 == bf)pSubL->_bf = -1;else if(-1 == bf)pParent->_bf = 1;
}
- 新节点插入较高右子树的左侧—右左:先右单旋再左单旋
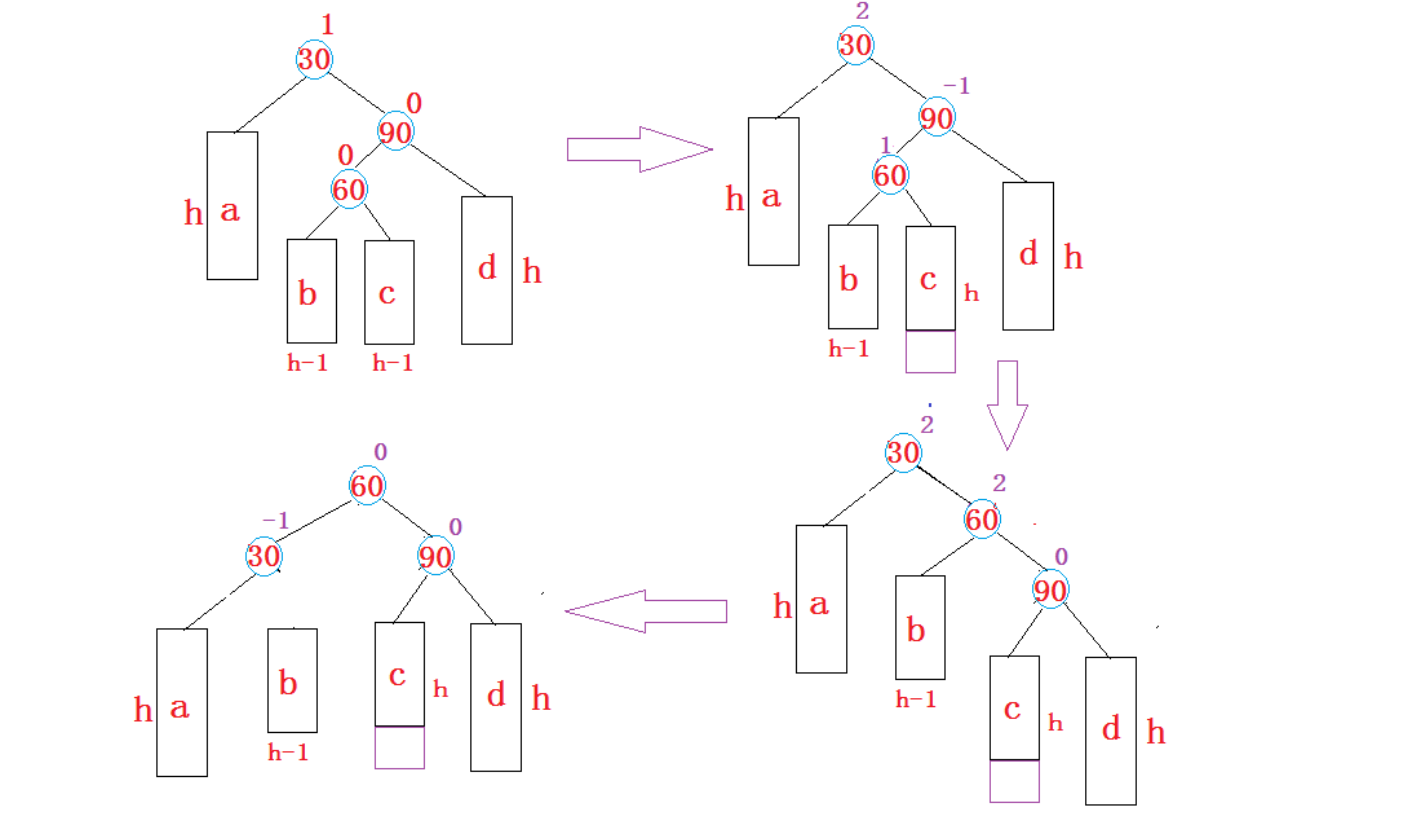
参考右左双旋。
总结:
假如以pParent为根的子树不平衡,即pParent的平衡因子为2或者-2,分以下情况考虑
- pParent的平衡因子为2,说明pParent的右子树高,设pParent的右子树的根为pSubR
- 当pSubR的平衡因子为1时,执行左单旋
- 当pSubR的平衡因子为-1时,执行右左双旋
- pParent的平衡因子为-2,说明pParent的左子树高,设pParent的左子树的根为pSubL
- 当pSubL的平衡因子为-1是,执行右单旋
- 当pSubL的平衡因子为1时,执行左右双旋
旋转完成后,原pParent为根的子树个高度降低,已经平衡,不需要再向上更新。
实现代码
#pragma oncetemplate<class K, class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf; // balance factorpair<K, V> _kv;AVLTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _bf(0), _kv(kv){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent){if (cur == parent->left){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = cur->_parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 旋转处理if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else{RotateRL(parent);}break;}else{// 插入之前AVL树就有问题assert(false);}}return true;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}parent->_bf = 0;subR->_bf = 0;}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}subL->_bf = 0;parent->_bf = 0;}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else if (bf == 1){subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}else if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else{assert(false);}}private:Node* _root = nullptr;
};
5 AVL树的验证
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
- 验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树
- 验证其为平衡树
- 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
- 节点的平衡因子是否计算正确
int _Height(PNode pRoot);
bool _IsBalanceTree(PNode pRoot)
{// 空树也是AVL树if (nullptr == pRoot) return true;// 计算pRoot节点的平衡因子:即pRoot左右子树的高度差int leftHeight = _Height(pRoot->_pLeft);int rightHeight = _Height(pRoot->_pRight);int diff = rightHeight - leftHeight;// 如果计算出的平衡因子与pRoot的平衡因子不相等,或者// pRoot平衡因子的绝对值超过1,则一定不是AVL树if (diff != pRoot->_bf || (diff > 1 || diff < -1))return false;// pRoot的左和右如果都是AVL树,则该树一定是AVL树return _IsBalanceTree(pRoot->_pLeft) && _IsBalanceTree(pRoot->_pRight);}
6 AVL树的删除(了解)
因为AVL树也是二叉搜索树,可按照二叉搜索树的方式将节点删除,然后再更新平衡因子,只不错与删除不同的时,删除节点后的平衡因子更新,最差情况下一直要调整到根节点的位置。具体实现学生们可参考《算法导论》或《数据结构-用面向对象方法与C++描述》殷人昆版。
AVL树是一种自平衡的二叉搜索树,它的删除操作与插入操作类似,但需要在删除节点后进行平衡操作以保持树的平衡性。
AVL树的删除操作可以分为以下几种情况:
- 如果待删除的节点是叶子节点,直接删除即可。
- 如果待删除的节点只有一个子节点,将子节点替代待删除节点的位置。
如果待删除的节点有两个子节点,可以选择以下两种方式进行删除:
- 找到待删除节点的前驱或后继节点,将其值复制到待删除节点,并将前驱或后继节点删除。
- 找到待删除节点的左子树中的最大值或右子树中的最小值,将其值复制到待删除节点,并将最大值或最小值节点删除。
删除节点后,需要从被删除节点的父节点开始向上回溯,检查每个祖先节点是否平衡。如果发现某个祖先节点不平衡,需要进行相应的旋转操作来恢复平衡。
7 AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即 l o g 2 ( N ) log_2 (N) log2(N)。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
AVL树是一种自平衡二叉搜索树,它的性能相对于普通的二叉搜索树更加稳定。AVL树的性能可以从以下几个方面来介绍:
-
查找操作:AVL树的查找操作与普通的二叉搜索树相同,时间复杂度为O(log n),其中n为树中节点的数量。由于AVL树是平衡的,所以查找操作的性能是稳定的。
-
插入和删除操作:AVL树在插入和删除节点时会进行自平衡操作,以保持树的平衡性。这些自平衡操作包括旋转和重新计算节点的平衡因子。插入和删除操作的时间复杂度也是O(log n),但由于需要进行自平衡操作,所以相对于普通二叉搜索树,AVL树的插入和删除操作可能会更耗时。
-
平衡性:AVL树的平衡性保证了树的高度始终保持在一个较小的范围内。具体来说,AVL树的任意节点的左右子树高度差不超过1。这种平衡性保证了查找、插入和删除操作的时间复杂度都能够保持在O(log n)。
-
空间复杂度:AVL树的空间复杂度与节点数量成正比,即O(n)。每个节点需要存储键值对以及额外的平衡因子信息。
总的来说,AVL树在查找操作上具有较好的性能,但在插入和删除操作上可能会稍微慢一些。然而,AVL树的平衡性保证了树的高度始终保持在一个较小的范围内,从而保证了整体的性能稳定性。
相关文章:

【C++庖丁解牛】自平衡二叉搜索树--AVL树
🍁你好,我是 RO-BERRY 📗 致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 🎄感谢你的陪伴与支持 ,故事既有了开头,就要画上一个完美的句号,让我们一起加油 目录 前言1 AVL树的概念2. AVL…...

ES5和ES6的深拷贝问题
深拷贝我们知道是引用值的一个问题,因为在拷贝的时候,拷贝的是在内存中同一个引用。所以当其中的一个应用值发生改变的时候,其他的同一个引用值也会发生变化。那么针对于这种情况,我们需要进行深度拷贝,这样就可以做到…...

阿里云发送短信配置
依赖 <dependency><groupId>org.apache.httpcomponents</groupId><artifactId>httpclient</artifactId><version>4.2.1</version> </dependency> <dependency><groupId>org.apache.httpcomponents</groupId&g…...

axios封装,请求取消和重试,请求头公共参数传递
axios本身功能已经很强大了,封装也无需过度,只要能满足自己项目的需求即可。 常规axios封装,只需要设置: 实现请求拦截实现响应拦截常见错误信息处理请求头设置 import axios from axios;// 创建axios实例 const service axios…...

隐私计算实训营学习五:隐语PSI介绍及开发指南
文章目录 一、SPU 实现的PSI介绍1.1 PSI定义和种类1.1.1 PSI定义和种类1.1.2 隐语PSI功能分层 1.2 SPU 实现的PSI介绍1.2.1 半诚实模型1.2.2 PSI实现位置 二、SPU PSI调度架构三、Secretflow PSI开发指南四、隐语PSI后续计划 一、SPU 实现的PSI介绍 1.1 PSI定义和种类 1.1.1 …...
ES的RestClient相关操作
ES的RestClient相关操作 Elasticsearch使用Java操作。 本文仅介绍CURD索引库和文档!!! Elasticsearch基础:https://blog.csdn.net/weixin_46533577/article/details/137207222 Elasticsearch Clients官网:https://ww…...

linux通用命令 ssh命令连接慢问题排查
系列文章目录 文章目录 系列文章目录一、 ssh 连接慢3.1 查找原因3.2 解决方案 一、 ssh 连接慢 最近的 koji 服务器 使用 ssh 连接很慢。 3.1 查找原因 可以通过 ssh -vvv 192.168.0.123 或 time ssh root192.168.0.123 exit 查找原因如下: SERVER的SSHD会去DN…...
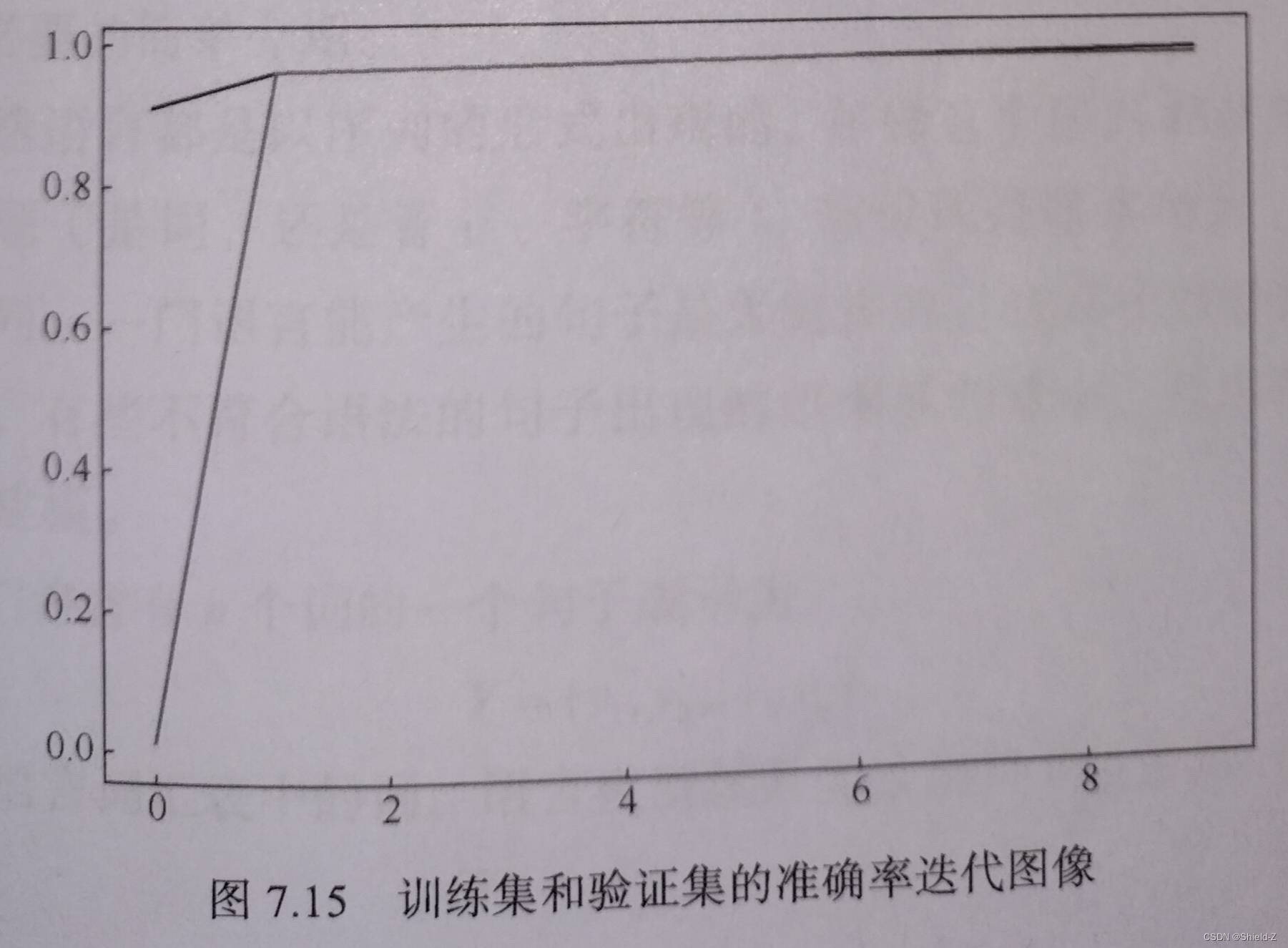
7.卷积神经网络与计算机视觉
计算机视觉是一门研究如何使计算机识别图片的学科,也是深度学习的主要应用领域之一。 在众多深度模型中,卷积神经网络“独领风骚”,已经被称为计算机视觉的主要研究根据之一。 一、卷积神经网络的基本思想 卷积神经网络最初由 Yann LeCun&a…...

Linux|如何管理多个Git身份
摘要 关于如何管理不同项目和多个Git身份。 作为一名通用软件开发者,我经常发现自己在处理各种各样的项目,每个项目都有自己的要求和期望。这包括为个人、工作和客户项目管理不同的Git身份。以下是我组织Git仓库以简化这一过程的方法。 目录组织 我将我的…...

力扣---最长回文子串---二维动态规划
二维动态规划思路: 首先,刚做完这道题:力扣---最长有效括号---动态规划,栈-CSDN博客,所以会有一种冲动,设立g[i],表示以第i位为结尾的最长回文子串长度,然后再遍历一遍取最大长度即可…...
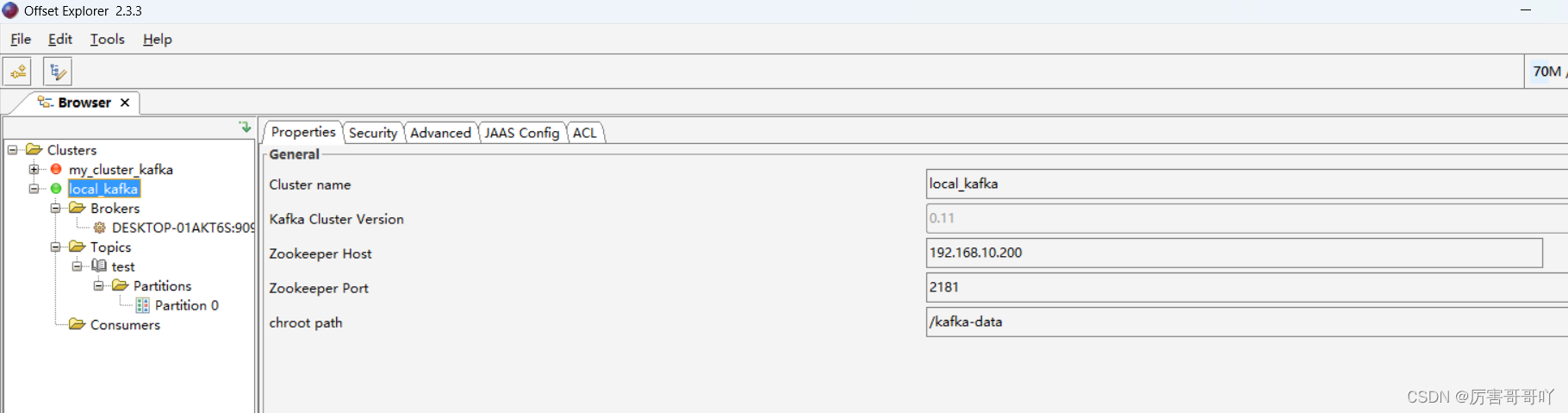
(一)kafka实战——kafka源码编译启动
前言 本节内容是关于kafka消息中间键的源码编译,并通过idea工具实现kafka服务器的启动,使用的kafka源码版本是3.6.1,由于kafka源码是通过gradle编译的,以及服务器是通过scala语言实现,我们要预先安装好gradle编译工具…...

Spring Boot 使用 Redis
1,Spring 是如何集成Redis的? 首先我们要使用jar包 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId></dependency><dependency><gro…...

火车头通过关键词采集文章的原理
随着互联网信息的爆炸式增长,网站管理员和内容创作者需要不断更新和发布新的文章,以吸引更多的用户和提升网站的排名。而火车头作为一款智能文章采集工具,在这一过程中发挥着重要作用。本文将探讨火车头如何通过关键词采集文章,以…...

Kafka 面试题及参考答案
目录 1. Kafka 的核心特性是什么? 2. Kafka 为什么能够实现高吞吐量? 3. Kafka 的消息丢失是...

【Qt 学习笔记】Day1 | Qt 背景介绍
博客主页:Duck Bro 博客主页系列专栏:Qt 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ Day1 | Qt 背景介绍 文章编号:Qt 学习笔记 / 01 文章目录…...

springboot3.2.4+Mybatis-plus在graalvm21环境下打包exe
springboot3.2.4Mybatis-plus在graalvm21环境下打包exe 前提条件为之前已经能直接打包springboot3.2.4项目了然后在此基础上接入Mybatis-plus,然后能够正常进行打包exe并且执行,参考之前的文章进行打包 核心配置如下 package com.example.demo.config…...

Kubernetes(K8S)学习(二):K8S常用组件
K8S常用组件 一、 Controllers1、ReplicationController(RC)2、ReplicaSet(RS)3、Deployment 二、Labels and Selectors三、Namespace(命名空间)1、简介2、测试2.1、创建namespace2.2、创建pod 四、Network1、集群内:同一个Pod中的容器通信2、…...
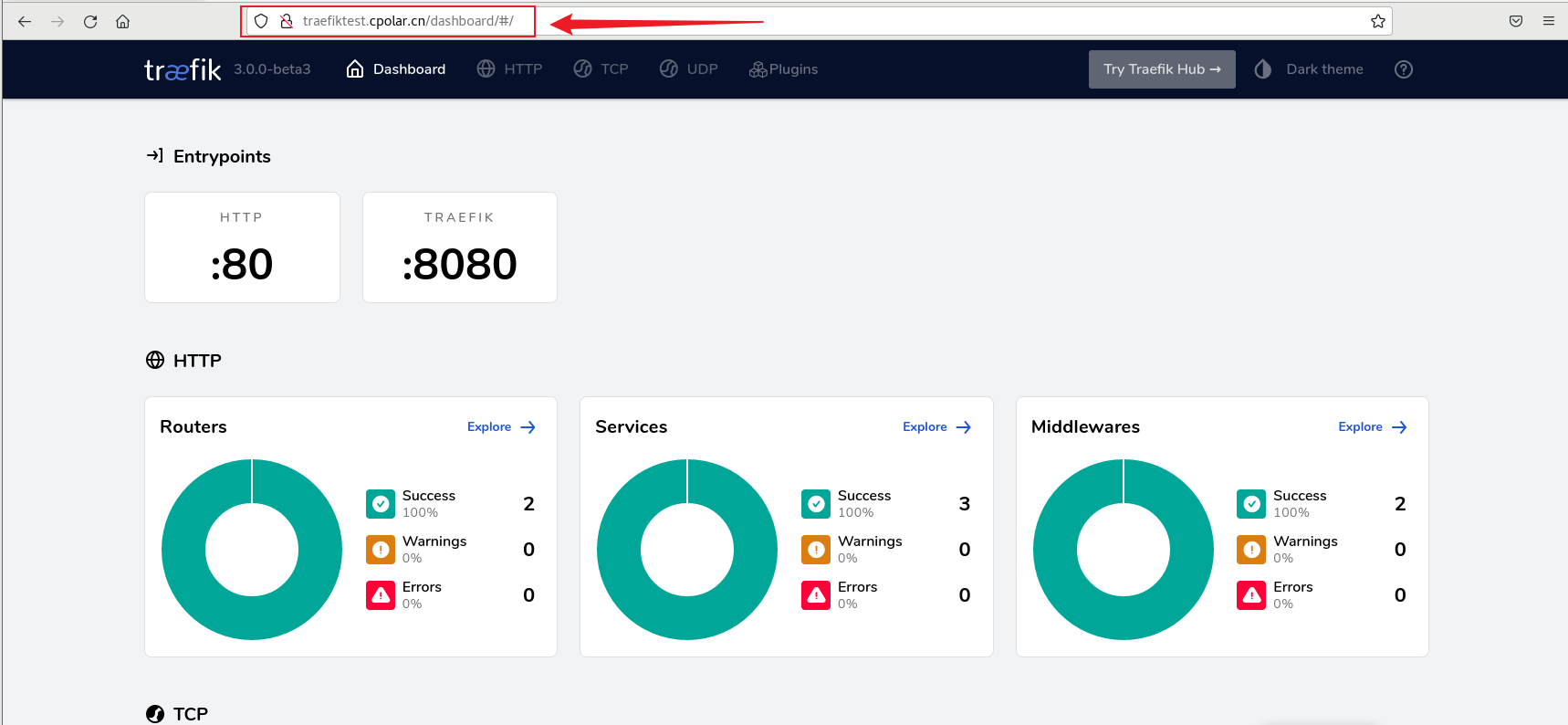
如何使用群晖WebDAV实现固定公网地址同步Zotero文献管理器
文章目录 前言1. Docker 部署 Trfɪk2. 本地访问traefik测试3. Linux 安装cpolar4. 配置Traefik公网访问地址5. 公网远程访问Traefik6. 固定Traefik公网地址 前言 Trfɪk 是一个云原生的新型的 HTTP 反向代理、负载均衡软件,能轻易的部署微服务。它支持多种后端 (D…...
【JavaSE】初识线程,线程与进程的区别
文章目录 ✍线程是什么?✍线程和进程的区别✍线程的创建1.继承 Thread 类2.实现Runnable接口3.匿名内部类4.匿名内部类创建 Runnable ⼦类对象5.lambda 表达式创建 Runnable ⼦类对象 ✍线程是什么? ⼀个线程就是⼀个 “执行流”. 每个线程之间都可以按…...
等级考试三级考试真题2023年9月——持续更新.....)
全国青少年软件编程(Python)等级考试三级考试真题2023年9月——持续更新.....
青少年软件编程(Python)等级考试试卷(三级) 分数:100 题数:38 一、单选题(共25题,共50分) 1.有一组数据存在列表中,things[“桌子”,“椅子”,“茶几”,“沙发”,“西瓜”,“苹果”,“草莓”,“…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
