信息工程大学第五届超越杯程序设计竞赛(同步赛)题解
比赛传送门
博客园传送门
c++ 模板框架
#pragma GCC optimize(3,"Ofast","inline")
#include<bits/stdc++.h>
#define rep(i,a,b) for (int i=a;i<b;++i)
#define per(i,a,b) for (int i=a;i>b;--i)
#define se second
#define fi first
#define endl '\n'
#define all(x) (x).begin(),(x).end()
#define pii pair<int,int>
#define pli pair<LL,int>
#define MEM(a,x) memset(a,x,sizeof(a))
#define lowbit(x) ((x)&-(x))
inline int Ls(int p){return p<<1;}
inline int Rs(int p){return p<<1|1;}
typedef long long LL;
typedef unsigned long long ULL;
using namespace std;
const int N=1e3+10;
inline void Solve()
{
}
int main()
{#ifndef ONLINE_JUDGEfreopen("1.in","r",stdin);freopen("1.out","w",stdout);#endifios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int _=1;//cin>>_;while(_--){Solve();}return 0;
}
A.遗失的旋律
把加一操作和乘二操作分开看,某一个位置出现了0表示加一,后面所有出现的1都会乘2,也就是说如果用cnt表示这个0后面1的个数,它对答案的贡献就是
对于一个给定的一个字串,答案就可以写成所有0产生的贡献之和,再加上
其中cnt表示整个区间1的个数。比如 010110 就可以写成
用线段树维护区间1的个数和区间所有0对答案贡献的总和,分别用s1和s0表示。左右合并时s0就可以用左树s0乘上右树s1,再加上右树的s0。
const int N=1e5+10,M=998244353;
char s[N];
inline int qp(int a,int b)
{int res=1;while(b){if(b&1) res=1ll*res*a%M;a=1ll*a*a%M;b>>=1;}return res%M;
}
struct sg_tree{int l,r;int s0,s1;
}T[8*N];
inline void up(int p)
{T[p].s1=T[Ls(p)].s1+T[Rs(p)].s1;T[p].s0=(1ll*T[Ls(p)].s0*qp(2,T[Rs(p)].s1)%M+T[Rs(p)].s0)%M;
}
inline sg_tree up(sg_tree L,sg_tree R)
{sg_tree t;t.s1=L.s1+R.s1;t.s0=(1ll*L.s0*qp(2,R.s1)%M+R.s0)%M;return t;
}
inline void build(int p,int l,int r)
{if(l==r){T[p]={l,r,s[l]=='0',s[l]=='1'};return;}T[p]={l,r};int mid=l+r>>1;build(Ls(p),l,mid);build(Rs(p),mid+1,r);up(p);
}
inline void upd(int p,int x)
{int &l=T[p].l,&r=T[p].r;if(l>x||r<x) return;if(l==r){s[l]=!(s[l]-'0')+'0';T[p].s0=(s[l]=='0');T[p].s1=(s[l]=='1');return;}upd(Ls(p),x);upd(Rs(p),x);up(p);
}
inline sg_tree qy(int p,int l,int r)
{sg_tree t={0,0,0,0},lt=t,rt=t;if(T[p].l>r||T[p].r<l) return t;if(T[p].l>=l&&T[p].r<=r) return T[p];if(T[Ls(p)].r>=l) lt=qy(Ls(p),l,r);if(T[Rs(p)].l<=r) rt=qy(Rs(p),l,r);return up(lt,rt);
}
inline void Solve()
{int n,m;cin>>n>>m>>s+1;build(1,1,n);while(m--){int op,x,l,r;cin>>op;if(op==1){cin>>x;upd(1,x);}else{cin>>x>>l>>r;sg_tree t=qy(1,l,r);cout<<(t.s0+1ll*x*qp(2,t.s1)%M)%M<<endl;}}
}B.时间的礼物
有很多方法可以求得方案数为:
首先可以将整数划分问题转换为隔板法问题:有n个球,m-1个隔板方案相当于是把n个数分解为m个大于0的数方案,题目要求可以等于0,n个球的左右两边可以插入隔板,这里可以增加两个球,对于隔板并在一起的情况可以在隔板之间插入球,增加了m-2个球,等价于n+m个球插入m-1个隔板的方案数,所以总方案数为:
从另外一个角度,考虑整数划分方案中0的个数为i,剩下的相当于是n个球,插入m-i-1个隔板方案数,总方案可以表示成,这个式子也等价于共有m+n-1个球,先从前面m个中选择i个,再从后面的n-1个球中选择m-i-1个,一共选择m-1个球。这个方案数也等价于直接在n+m-1个球中选m-1个方案数。
直接计算可能会存在逆元不存在的情况,可以先用素数筛找出内的素数(式子中m+n数量级可能会达到2e6),可以计算每个素数在阶乘中出现的次数,进一步算出每个素数在答案中的阶乘。
const int N=2e6+10;
int n,m,p;
int cnt,pr[N];
bool st[N];
inline void INIT()
{rep(i,2,N){if(!st[i]) pr[++cnt]=i;for(int j=1;j<=cnt&&i*pr[j]<=N-1;++j){st[i*pr[j]]=1;if(i%pr[j]==0) break;}}
}
inline int Qp(int a,int b)
{int res=1;while(b){if(b&1) res=1ll*res*a%p;a=1ll*a*a%p;b>>=1;}return res%p;
}
inline int Cal(int a,int b)
{int res=0;while(a){res+=a/b;a/=b;}return res;
}
inline void Solve()
{INIT();cin>>n>>m>>p;int ans=1;rep(i,1,cnt+1){int t=Cal(n+m-1,pr[i])-Cal(m-1,pr[i])-Cal(n,pr[i]);ans=1ll*ans*Qp(pr[i],t)%p;}cout<<ans<<endl;
}C.财政大臣
用一个数组记录变化的值,修改只需要改变单个点的值,最后从根节点做一遍dfs,记录前面节点变化值的和加到子节点上。最后答案就是变化的值加上初始的值。
const int N=1e5+10,M=2*N;
int h[N],e[M],ne[M],idx;
int a[N];
LL b[N];
inline void add(int a,int b)
{e[++idx]=b;ne[idx]=h[a];h[a]=idx;
}
void dfs(int u,int fa,int s)
{for(int i=h[u];i;i=ne[i]){int v=e[i];if(v==fa) continue;dfs(v,u,b[u]+s);}b[u]+=s;
}
inline void Solve()
{int n,m;cin>>n>>m;rep(i,0,n-1){int a,b;cin>>a>>b;add(a,b);add(b,a);}rep(i,1,n+1) cin>>a[i];while(m--){int op,u,x;cin>>op>>u>>x;if(op==1) b[u]+=x;else b[u]-=x;}dfs(1,0,0);rep(i,1,n+1) cout<<a[i]+b[i]<<" ";
}
D.实验室有多少人
用数对维护信息,开始时间对应1,表示增加1个人,结束时间对应-1,表示减少一个人。把所有数对按时间从小到大排序,相同时间的把-1的放在前面,最后遍历更新答案即可。
const int N=1e6+10;
pii a[2*N];
inline void Solve()
{int n,x,y,m=0;cin>>n;rep(i,0,n){cin>>x>>y;a[++m]={x,1};a[++m]={y,-1};}sort(a+1,a+1+m);int ans=0,nw=0;rep(i,1,m+1){nw+=a[i].se;ans=max(ans,nw);}cout<<ans<<endl;
}
E.在雾中寻宁静
先对树做一遍dfs,记录节点进入的时间L和出去的时间R,L到R就包含了该节点以及其子树节点(dfs序)。
问题转换为区间染色,因为后面的染色会覆盖前面的染色,可以考虑逆向操作,每一次只染没有染过色的点,跳过已经染过色的点。可以用并查集维护下一个未染色的点。
代码说明:
- a数组表示dfs序。
- L[i]和R[i]分别表示进入和出去时刻。
- s[i]表示i指向下一个没有填色的位置。
const int N=2e5+10,M=2*N;
int h[N],e[N],ne[N],idx;
int a[M],L[N],R[N];
int n,cnt,s[M];
pii op[N];
inline void add(int a,int b)
{e[++idx]=b;ne[idx]=h[a];h[a]=idx;
}
void dfs(int u)
{L[u]=++cnt;for(int i=h[u];i;i=ne[i]) dfs(e[i]);R[u]=++cnt;
}
int Find(int u)
{if(s[u]==u) return u;else return s[u]=Find(s[u]);
}
inline void Solve()
{cin>>n;rep(i,1,n){int x;cin>>x;add(x,i+1);}dfs(1);int q;cin>>q;rep(i,0,q){int x,y;cin>>x>>y;op[i]={x,y};}rep(i,1,2*n+2) s[i]=i;per(i,q-1,-1){int l=L[op[i].fi],r=R[op[i].fi],c=op[i].se;for(int k=Find(l);k<=r;k=Find(k)){a[k]=c;s[k]=Find(k+1);}}rep(i,1,n+1) cout<<a[L[i]]<<" ";
}
F.不规则的轮回
注意到x,y的规模不大,对n个数对暴力求出所有数对最多枚举左右,时间上可以接收,空间上只需要存储询问中的数对,然后计算出的数对在询问中就算上贡献,c++用map即可。
const int N=2e3+10;
pii a[N],b[N];
inline void Solve()
{int n,m;set<pii>q;map<pii,int>mp;cin>>n;rep(i,0,n) cin>>a[i].fi>>a[i].se;cin>>m;rep(i,0,m) cin>>b[i].fi>>b[i].se,q.insert({b[i].fi,b[i].se});rep(i,0,n){int &x=a[i].fi,&y=a[i].se;while(x!=y){if(q.count({x,y})) ++mp[{x,y}];if(x>y) x-=y;else y-=x;}if(q.count({x,y})) ++mp[{x,y}];}rep(i,0,m) cout<<mp[{b[i].fi,b[i].se}]<<endl;
}
G.完美数字
根据算术基本定理将数字分成素数乘积,除了素数2和5结合对末尾0有贡献,其他素数乘积都不会产生新的末尾0,末尾的0个数就取决于2的幂次和5的幂次中较小的一个。
将每个数2的幂次和5的幂次计算出来,分别求前缀和。然后枚举左端点 L,找到第一个较小的段和大于等于 k 的右端点 R,对答案产生 n-R+1 的贡献。注意到 L 往右移动时,R 只能右前移,不能回退(双指针算法)。
const int N=2e5+10;
int a[N],b[N];
inline int A(int x,int k)
{int rt=0;while(x%k==0){x/=k;++rt;}return rt;
}
inline void Solve()
{int n,m;cin>>n>>m;rep(i,1,n+1){cin>>a[i];b[i]=A(a[i],2);a[i]=A(a[i],5);}rep(i,1,n+1) a[i]+=a[i-1],b[i]+=b[i-1];LL ans=0;int r=1;rep(l,1,n+1){while(r<=n&&min(a[r]-a[l-1],b[r]-b[l-1])<m) ++r;if(r<=n) ans+=n-r+1;}cout<<ans<<endl;
}
H.春天与花儿
如果只改变一个数,将 ai 加到 k 的倍数即可。
对于 k=4 的情况,还有可能是把两个不同的数加到能被2整除。
对于 k=6 的情况,还有可能是把一个数加到能被2整除,另外一个加到能被3整除。
const int N=1e6+10;
int a[N],n,b[N];
inline int calc(int x,int k)
{return (k-x%k)%k;
}
inline pii Find01(int *a)
{int m1=100,m2=100;rep(i,0,n){if(a[i]<=m1){m2=m1;m1=a[i];}else if(a[i]<m2) m2=a[i];}return {m1,m2};
}
inline int Find0(int *a)
{int pos=0;rep(i,1,n){if(a[i]<a[pos]){pos=i;}}return pos;
}
inline void Solve()
{int k,ans=6;cin>>n>>k;rep(i,0,n){cin>>a[i];ans=min(ans,calc(a[i],k));}if(k==4&&n!=1){rep(i,0,n) a[i]=calc(a[i],2);auto rt=Find01(a);ans=min(ans,rt.fi+rt.se);}if(k==6&&n!=1){rep(i,0,n) b[i]=calc(a[i],3),a[i]=calc(a[i],2);int p1=Find0(a),p2=Find0(b);if(p1!=p2){ans=min(ans,a[p1]+b[p2]);}else{auto r1=Find01(a),r2=Find01(b);ans=min({ans,r1.fi+r2.se,r1.se+r2.fi});}}cout<<ans<<endl;
}
I.孤独与追求
为了避免偶数回文串的情况,先对原字符串做填充处理。然后枚举中点,可以用二分长度+字符串哈希求出以这个点为中点的最长回文串。预处理出值的前缀和数组a,根据回文串对称性,对于中点是 m,右端点是 r 的回文串,只需要求出,用线段树维护区间最大值即可。
const int N=2e6+10;
int n,mp[27];
char s[N];
LL a[N];
ULL h[N],rh[N],p[N];
namespace Segment_tree{struct sg_tree{int l,r;LL mx;};inline void up(sg_tree *t,int p){t[p].mx=max(t[Ls(p)].mx,t[Rs(p)].mx);}inline void Build(sg_tree *t,LL *a,int p,int l,int r){t[p]={l,r};if(l==r){t[p].mx=a[l];return;}int mid=l+r>>1;Build(t,a,Ls(p),l,mid);Build(t,a,Rs(p),mid+1,r);up(t,p);}inline LL Qy(sg_tree *t,int p,int l,int r){if(t[p].l>r||t[p].r<l) return -1e18;if(t[p].l>=l&&t[p].r<=r) return t[p].mx;LL res=-1e18;if(t[Ls(p)].r>=l) res=max(res,Qy(t,Ls(p),l,r));if(t[Rs(p)].l<=r) res=max(res,Qy(t,Rs(p),l,r));return res;}
}
namespace Str_Algorithm{ULL Str_Hash(char *s){ULL p=131,h=0;int n=strlen(s);rep(i,0,n) h=h*p+s[i];return h;}ULL Str_Hash(string s){ULL p=131,h=0;rep(i,0,s.size()) h=h*p+s[i];return h;}void Build_lhash(char *s,ULL *h){int n=strlen(s+1);int p=131;h[0]=0;rep(i,1,n+1) h[i]=h[i-1]*p+s[i];}void Build_lhash(string s,ULL *h){int n=s.size()-1;int p=131;h[0]=0;rep(i,1,n+1) h[i]=h[i-1]*p+s[i];}void Build_rhash(char *s,ULL *h){int n=strlen(s+1);int p=131;h[n+1]=0;per(i,n,0) h[i]=h[i+1]*p+s[i];}void Build_rhash(string s,ULL *h){int n=s.size()-1;int p=131;h[n+1]=0;per(i,n,0) h[i]=h[i+1]*p+s[i];}ULL Get_lhash(int l,int r,ULL *h,ULL *p){return h[r]-h[l-1]*p[r-l+1];}ULL Get_rhash(int l,int r,ULL *h,ULL *p){return h[l]-h[r+1]*p[r-l+1];}void Manacher(char *s,int *p,int n){int r=0,c;rep(i,1,n){if(i<r) p[i]=min(p[(c<<1)-i],p[c]+c-i);else p[i]=1;while(s[p[i]+i]==s[i-p[i]]) ++p[i];if(p[i]+i>r) r=p[i]+i,c=i;}}
}
inline void Init(char *s,int &n)
{per(i,n,0) s[2*i-1]=s[i];n=2*n-1;for(int i=2;i<=n;i+=2) s[i]='z'+1;
}
Segment_tree::sg_tree T[4*N];
inline void Solve()
{using namespace Str_Algorithm;using namespace Segment_tree;cin>>n;rep(i,0,26) cin>>mp[i];cin>>s+1;Init(s,n);rep(i,1,n+1) a[i]=a[i-1]+mp[s[i]-'a'];p[0]=1;Build(T,a,1,1,n);rep(i,1,n+1) p[i]=p[i-1]*131;Build_lhash(s,h);Build_rhash(s,rh);LL ans=-1e18;rep(i,1,n+1){int l=0,r=min(n-i,i-1);while(l<r){int mid=l+r+1>>1;if(Get_lhash(i-mid,i,h,p)==Get_rhash(i,i+mid,rh,p)) l=mid;else r=mid-1;}ans=max(ans,2*(Qy(T,1,i,i+l)-a[i])+mp[s[i]-'a']);}cout<<ans<<endl;
}
J.最后的星光
如果用两个字符串相同位置个数来表示一个状态,最终状态就是字符串长度 n,发现问题转换成广搜。
如果当前状态是 t ,采用第一种方法可以枚举选了 i 个相同的位置,状态就转移到了 t-i+m-i。注意需要满足不相等的位置足够选:。采用第二种方法,假设在相等的位置中有 i 个在 a 中,j 个在 b 中,相同位置增加了a-i个,又减少了j个,状态转移到了 t+a-i-j。直接枚举 i+j 的值,上界就是
,下界要保证不相等的位置足够选:
时间复杂度为
const int N=2010;
char s1[N],s2[N];
int d[N];
inline void Solve()
{int a,b,m;cin>>s1>>s2>>a>>b>>m;int n=strlen(s1),ct=0;rep(i,0,n) if(s1[i]==s2[i]) ++ct;MEM(d,-1);d[ct]=0;queue<int>q;q.emplace(ct);while(q.size()){int t=q.front();q.pop();rep(i,max(0,m-n+t),t+1){if(t+m-2*i<0) break;if(d[t+m-2*i]==-1){q.emplace(t+m-2*i);d[t+m-2*i]=d[t]+1;}}rep(i,max(0,a+b-n+t),min(t,a+b)+1){if(t+a-i<0) break;if(d[t+a-i]==-1){q.emplace(t+a-i);d[t+a-i]=d[t]+1;}}}cout<<d[n]<<endl;
}
K.天使的拼图
结论是矩形满足3|n且4|m,或12|n且m>=7都合法,其中n,m可以互换。
假设n是行,m是列,由于n,m可交换,下面证明只说明一种。
考虑把两个Tenshi图块拼在一起,覆盖要求中间不能有空,只有两个拼法:
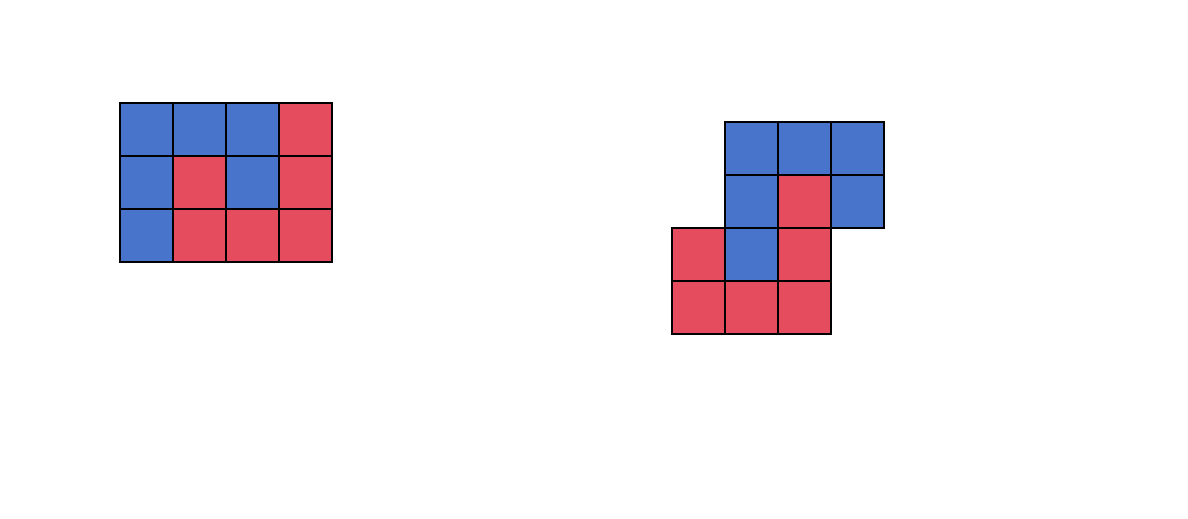
由于其他的拼法会导致中间有空隙不合法,问题就可以转换用上面两种图形经过旋转翻转覆盖矩形。
两个图形都是12块单位,如果能覆盖则一定有 12|nm
分类讨论:
- 3|n且4|m,此时显然能被上面第一个3 * 4的矩形图覆盖。
- 12|n,3|m或者4|m同1。下面考虑12|n,3和4都不能整除m,由上面两个图可知m>=3,得到m>=5。可验证m=5的情况无法覆盖。对于其他情况,如果m=3k+4,k>=1,使用第一个图,可以先把第一个3 * 4的图先横着放满,这时m=3k,后面都竖着放。如果m=3k+8,k>=1,横着放两次m就变成了 3k,也可以覆盖。
- 12|mn,m和n都不能被4整除。可知m和n都必须是偶数。将n * m的矩形分成单位正方形,将行和列分别标上号码1,2,…,n及1,2,…,m。给单位正方形(i,j)按如下方式赋值:值为i,j中能被4整除的数的个数(因此值可以为0,1,2)。这样所有的方格数字之和是偶数:考虑某个行i能被4整除产生贡献为m,对于能被4整除的列产生贡献为n,而m和n都是偶数。按照这个方法写一个程序打表,可以发现两个图不管如何放,贡献都是奇数。所以覆盖图形的个数也是偶数个,就有24|mn,则8|mn,m,n都为偶数,一定有一个被4整除,与前提矛盾,这种情况不存在。
bool ok(LL n,LL m)
{if(n%3==0&&m%4==0) return true;if(n%12==0&&m>=7) return true;return false;
}
inline void Solve()
{LL n,m;cin>>n>>m;if(ok(n,m)||ok(m,n)) cout<<"Yes"<<endl;else cout<<"No"<<endl;
}
L.擅长搞事的高木同学
如下图所示,假设要从A点走到对角E点。首先可以发现A到E最后一定是偶数步,且至少4步。
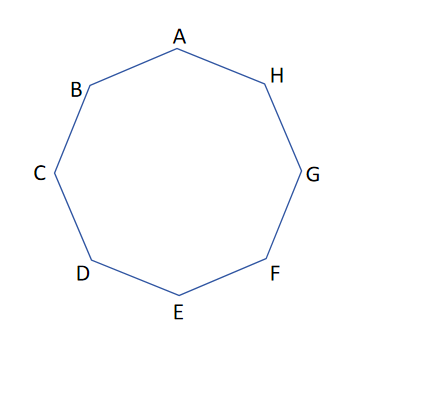
用 ,分别表示点 A,C,G到E的方案数。
注意到对称性,可知
我们可以对 进行划分,从A开始走两步,可以到达A,C,G,于是有了下式(注意到达A是A->B->A和A->H->A两种不同的走法):
再对 进行划分,从C开始走两步,可以到达C,A,于是有了下式:
边界:
写成矩阵形式用快速幂即可:
const int N=1e3+10,M=1e9+7;
struct mat{int a[2][2];mat operator*(const mat& b) const{mat c={0,0,0,0};rep(i,0,2) rep(j,0,2) rep(k,0,2) c.a[i][j]+=1ll*a[i][k]*b.a[k][j]%M,c.a[i][j]%=M;return c;}
};
inline int Qp(LL n)
{mat res={1,0,0,1},A={2,2,1,2},a={0,0,1,0};while(n){if(n&1) res=res*A;A=A*A;n>>=1;}res=res*a;return res.a[0][0]%M;
}
inline void Solve()
{LL n;cin>>n;if((n&1)||n<=3){cout<<0<<endl;}else cout<<Qp(n/2-1)<<endl;
}
M.Monika's game
用f(n)表示n的最大值。无论用什么策略,最大值始终是
证明:
对于n=1该式子成立。
对于,假设比n小的规模都满足上式,则有:
故对于,上式也成立。
inline void Solve()
{int n;cin>>n;cout<<1ll*n*(n-1)/2<<endl;
}
相关文章:
信息工程大学第五届超越杯程序设计竞赛(同步赛)题解
比赛传送门 博客园传送门 c 模板框架 #pragma GCC optimize(3,"Ofast","inline") #include<bits/stdc.h> #define rep(i,a,b) for (int ia;i<b;i) #define per(i,a,b) for (int ia;i>b;--i) #define se second #define fi first #define e…...

Python:文件读写
一、TXT文件读写 Python中用open()函数来读写文本文件,返回文件对象,以下是函数语法。 open(<name>, <mode>, <buffering>,<encoding)name:文件名。 mode:打开文件模式。 buffering:设…...

10.windows ubuntu 组装软件:spades,megahit
Spades 是一种用于组装测序数据的软件,特别适用于处理 Illumina 测序平台产生的数据。它的全称是 "St. Petersburg genome assembler",是一款广泛使用的基因组组装工具。 第一种:wget https://cab.spbu.ru/files/release3.15.3/S…...

K8S之Secret的介绍和使用
Secret Secret的介绍Secret的使用通过环境变量引入Secret通过volume挂载Secret Secret的介绍 Secret是一种保护敏感数据的资源对象。例如:密码、token、秘钥等,而不需要把这些敏感数据暴露到镜像或者Pod Spec中。Secret可以以Volume或者环境变量的方式使…...
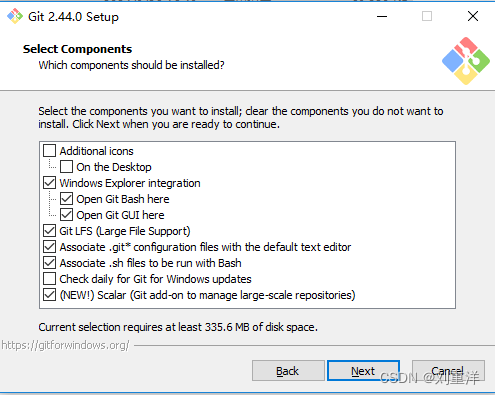
git下载安装教程
git下载地址 有一个镜像的网站可以提供下载: https://registry.npmmirror.com/binary.html?pathgit-for-windows/图太多不截了哈哈,一直next即可。...
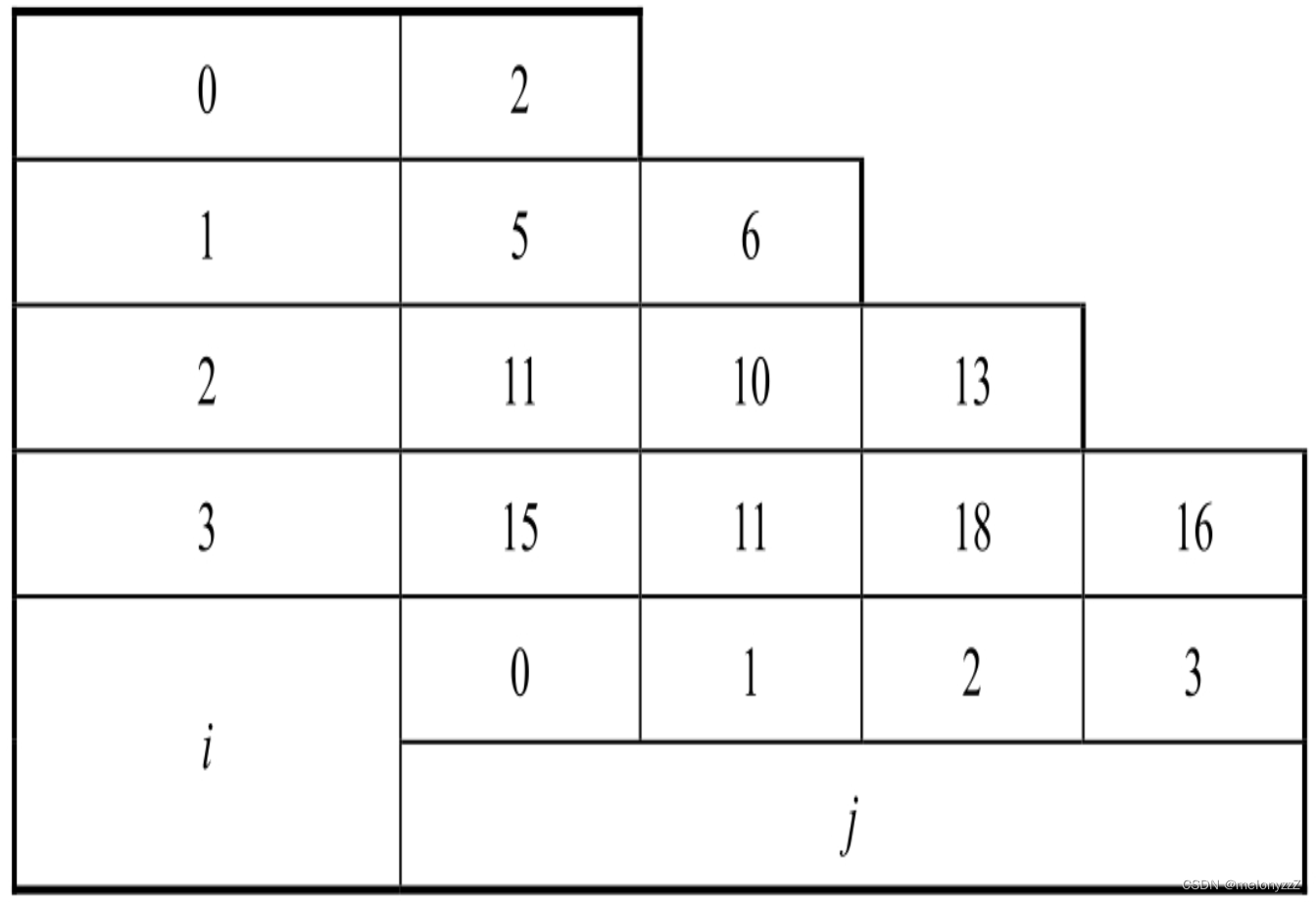
《剑指 Offer》专项突破版 - 面试题 98、99 和 100 : 和动态规划相关的矩阵路径问题(C++ 实现)
目录 前言 面试题 98 : 路径的数目 面试题 99 : 最小路径之和 面试题 100 : 三角形中最小路径之和 前言 矩阵路径是一类常见的可以用动态规划来解决的问题。这类问题通常输入的是一个二维的格子,一个机器人按照一定的规则从格子的某个位置走到另一个位置&#…...
)
KY145 EXCEL排序(用Java实现)
描述 Excel可以对一组纪录按任意指定列排序。现请你编写程序实现类似功能。 对每个测试用例,首先输出1行“Case i:”,其中 i 是测试用例的编号(从1开始)。随后在 N 行中输出按要求排序后的结果,即:当 C…...

属性选择器
1.[title]{background:yellow;}:所有带title标签设置成黄色 2.div[class]{background:yellow;}:所有div中带class标签设置成黄色 3.div[classbox1]{border:1px solid blue; }:div中包含class并且classbox1的设置成蓝边框 4. class…...

软考 - 系统架构设计师 - 关系模型的完整性规则
前言 关系模型的完整性规则是一组用于确保关系数据库中数据的完整性和一致性的规则。这些规则定义了在关系数据库中如何存储、更新和查询数据,以保证数据的准确性和一致性。 详情 关系模型的完整性规则主要包括以下三类: 实体完整性规则 这是确保每个…...

写了几个难一点的sql
写了几个难一点的sql SELECT bn.id AS book_node_id, t.version_id, bn.textbook_id, s.id AS subject_id, s.stage_id, COUNT( CASE WHEN d.document_type_id 1 AND d.scope IS NULL AND p.document_id IS NOT NULL THEN 1 END ) AS type_1_count, COUNT( CASEWHEN d.docume…...
【JDK常用的API】包装类
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【Java】 【VulnHub靶场复现】【面试分析】 🎉点赞➕评论➕收藏 …...
黑暗模式适配的实现)
Android Q(10)黑暗模式适配的实现
一、引言 随着 AndroidQ(10)的发布,黑暗模式成为了系统级别的特性。为了满足用户在不同环境下的使用需求,应用程序需要及时进行黑暗模式的适配。本文将详细介绍如何在 AndroidQ(10)上实现黑暗模式的适配&a…...
【git】git使用手册
目录 一 初始化 1.1 账号配置 1.2 ssh生成 1.2.1 配置ssh 1.2.2 测试SSH 1.3 初始化本地仓库并关联远程仓库 二 使用 2.1 上传 2.2 拉取 三 问题 3.1 关联失败 一 初始化 git的安装很简单,下载后大部分进行下一步完成即可----->地址: git工具下载 1.1 账号配置…...

unity中判断方向 用 KeyVertical ,KeyHorizontal 判断ui物体的 方向
float KeyVertical Input.GetAxis("Vertical"); float KeyHorizontal Input.GetAxis("Horizontal"); // 假设 UI 物体在竖直方向上为 Y 轴,水平方向上为 X 轴 Vector2 direction new Vector2(KeyHorizontal, KeyVertical); if (direction…...

前端a4纸尺寸转像素尺寸
前端必备工具推荐网站(免费图床、API和ChatAI等实用工具): http://luckycola.com.cn/ 一、a4纸张有多大 A4纸的尺寸是210mm297mm,也就是21.0cm29.7cm, A4纸尺寸转屏幕像素尺寸和屏幕分辨率有关,首先1英寸2.54cm, 如果屏幕DPI分辨率为72像素/英寸,换算一下ÿ…...

Android 中 调试和减少内存错误
Android 中 调试和减少内存错误 ASan 概述 官网连接: https://developer.android.com/ndk/guides/asan?hlzh-cn ASan API 27开始HWASan(替换AScan) 从 NDK r21 和 Android 10(API 级别 29)开始适用于 64 位 Arm 设…...

证券市场概述
证券市场 证券市场参与者证券发行市场(一级市场)证券发行方式(按发行对象)证券发行方式(按有无中介)证券交易市场(二级市场)证券交易所场外交易市场(店头市场、柜台市场&…...

什么是数据结构
一、什么是数据结构 1.数据结构研究计算机数据间的关系 2.包括数据的逻辑结构和储存结构及其操作 数据的逻辑结构:表示数据运算之间的抽象关系 按每个元素可能具有的直接前趋数和后继数将逻辑结构分为“线性结构”和“非线性结构”两大类 数据的储存结构&#…...

基于springboot+vue实现的学校田径运动会管理系统
作者主页:Java码库 主营内容:SpringBoot、Vue、SSM、HLMT、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、小程序、安卓app等设计与开发。 收藏点赞不迷路 关注作者有好处 文末获取源码 技术选型 【后端】:Java 【框架】:spring…...

HarmonyOS 应用开发之FA模型绑定Stage模型ServiceExtensionAbility
本文介绍FA模型的三种应用组件如何绑定Stage模型的ServiceExtensionAbility组件。 PageAbility关联访问ServiceExtensionAbility PageAbility关联访问ServiceExtensionAbility和PageAbility关联访问ServiceAbility的方式完全相同。 import featureAbility from ohos.ability…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
