《剑指 Offer》专项突破版 - 面试题 98、99 和 100 : 和动态规划相关的矩阵路径问题（C++ 实现）

目录

前言

面试题 98 : 路径的数目

面试题 99 : 最小路径之和

面试题 100 : 三角形中最小路径之和

---

 

---

前言

矩阵路径是一类常见的可以用动态规划来解决的问题。这类问题通常输入的是一个二维的格子，一个机器人按照一定的规则从格子的某个位置走到另一个位置，要求计算路径的条数或找出最优路径。

矩阵路径相关问题的状态转移方程通常有两个参数，即 f(i, j) 的两个参数 i、j 通常是机器人当前到达的坐标。需要根据路径的特点找出到达坐标 (i, j) 之前的位置，通常是坐标 (i - 1, j - 1)、(i - 1, j)、(i, j - 1) 中的一个或多个。相应地，状态转移方程就是找出 f(i, j) 与 f(i - 1, j - 1)、f(i - 1, j) 或 f(i, j - 1) 的关系。

可以根据状态转移方程写出递归代码，但值得注意的是一定要将 f(i, j) 的结果用一个二维数组缓存，以避免不必要的重复计算。也可以将计算所有 f(i, j) 看成填充二维表格的过程，相应地，可以创建一个二维数组并逐一计算每个元素的值。通常，矩阵路径相关的问题的代码都可以优化空间效率，用一个一维数组就能保存所有必需的数据。

接下来列举几个高频的矩阵类型的问题。

---

面试题 98 : 路径的数目

题目：

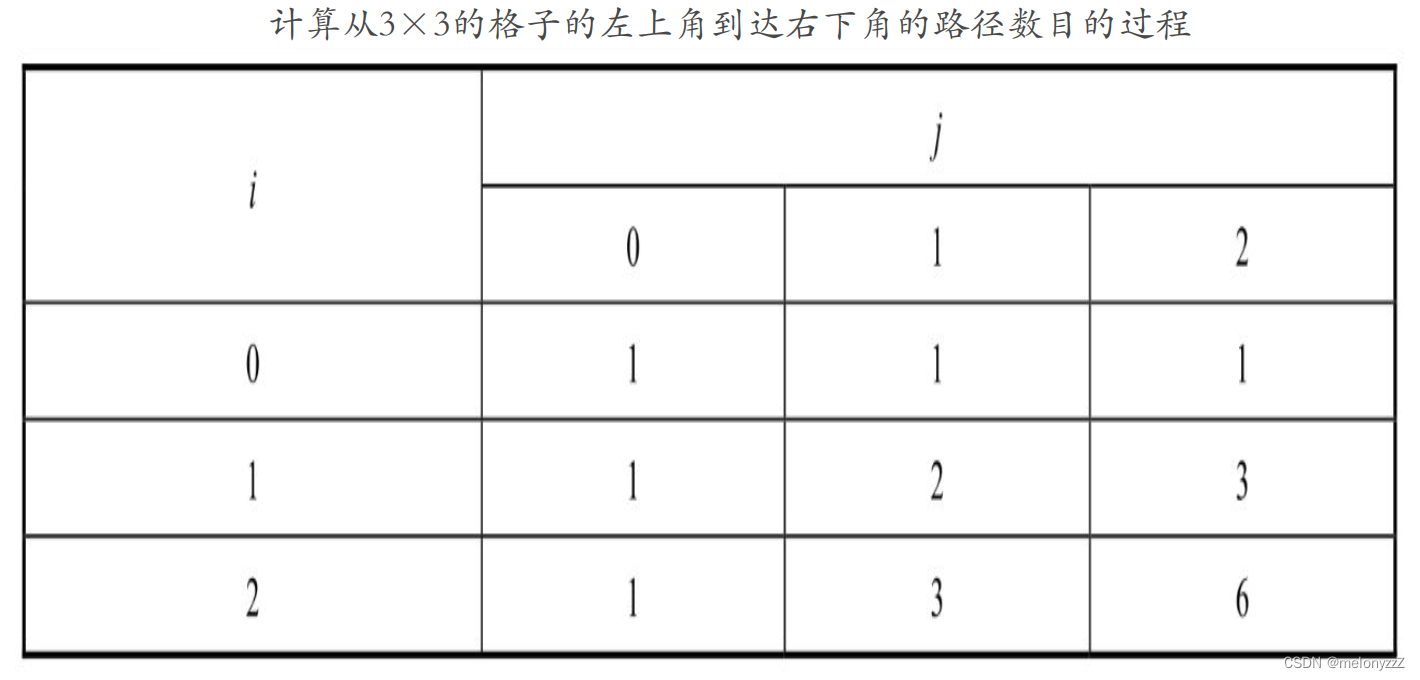
一个机器人从 m x n 的格子的左上角出发，它每步要么向下要么向右，直到抵达格子的右下角。请计算机器人从左上角到达右下角的路径的数目。例如，如果格子的大小是 3 x 3，那么机器人从左上角到达右下角有 6 条符合条件的不同路径，如下图所示。

分析：

机器人每次只能走一步，它从格子的左上角到达右下角需要走多步。机器人每走一步都有两个选择，要么向下走要么向右走。一个任务需要多个步骤才能完成，每步面临若干选择，这类问题看起来可以用回溯法解决，但由于这个题目只要求计算从左上角到达右下角的路径的数目，并没有要求列出所有的路径，因此这个问题更适合用动态规划解决。

分析确定状态转移方程：

应用动态规划解决问题的关键在于找出状态转移方程。可以用函数 f(i, j) 表示从格子的左上角坐标为 (0, 0) 的位置出发到达坐标为 (i, j) 的位置的路径的数目。如果格子的大小为 m x n，那么 f(m - 1, n - 1) 就是问题的解。

1. 当 i 等于 0 时，机器人位于格子最上面一行，机器人不可能从某个位置向下走一步到达一个行号 i 等于 0 的位置。因此，f(0, j) 等于 1，即机器人只有一种方法可以到达坐标为 (0, j) 的位置，即从 (0, j - 1) 的位置向右走一步。

2. 当 j 等于 0 时，机器人位于格子最左边的一列，机器人不可能从某个位置向右走一步到达一个行号 j 为 0 的位置，因此，f(i, 0) 等于 1，即机器人只有一种方法可以到达坐标为 (i, 0) 的位置，即从 (i - 1, 0) 的位置向下走一步。

3. 当行号 i、列号 j 都大于 0 时，机器人有两种方法可以到达坐标为 (i, j) 的位置。它既可以从坐标 (i - 1, j) 的位置向下走一步，也可以从坐标 (i, j - 1) 的位置向右走一步，因此，f(i, j) 等于 f(i - 1, j) 与 f(i, j - 1) 之和。

class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 1));for (int i = 1; i < m; ++i){for (int j = 1; j < n; ++j){dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};

上述代码用一个二维数组 dp 保存 f(i, j) 的计算结果，f(i, j) 保存在 dp[i][j] 中。

上述代码的时间复杂度和空间复杂度都是 O(mn)。

优化空间效率：

接下来尝试优化代码的空间效率。在计算 f(i, j) 时只需要用到 f(i - 1, j) 和 f(i, j - 1) 的值，因此只需要保存标号分别为 i - 1 和 i 的两行就可以。如果创建一个只有两行的二维数组 dp，将 f(i, j) 保存在 dp[i % 2][j] 中，那么就将空间复杂度优化到 O(n)。

还可以进一步优化空间效率，只需要创建一个一维数组 dp 就可以。在计算 f(i, j) 时需要用到 f(i - 1, j) 和 f(i, j - 1) 的值。接下来在计算 f(i, j + 1) 时需要用到 f(i - 1, j + 1) 和 f(i, j) 的值。在计算完 f(i, j) 之后就不再需要 f(i - 1, j) 的值。在二维表格中，f(i, j) 和 f(i - 1, j) 是上下相邻的两个位置。由于在用 f(i - 1, j) 计算出 f(i, j) 之后就不再需要 f(i - 1, j)，因此可以只用一个位置来保存 f(i - 1, j) 和 f(i, j) 的值。这个位置在计算 f(i, j) 之前保存的是 f(i - 1, j) 的值，计算 f(i, j) 之后保存的是 f(i, j) 的值。由于每个位置能够用来保存两个值，因此只需要一个一维数组就能保存表格中的两行。

class Solution {
public:int uniquePaths(int m, int n) {vector<int> dp(n, 1);for (int i = 1; i < m; ++i){for (int j = 1; j < n; ++j){dp[j] += dp[j - 1];}}return dp[n - 1];}
};

上述代码的时间复杂度仍然是 O(mn)，但空间复杂度被优化到 O(n)。

---

面试题 99 : 最小路径之和

题目：

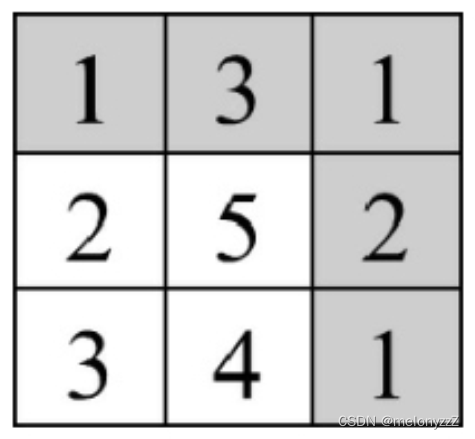
在一个 m x n（m、n 均大于 0）的格子中，每个位置都有一个数字。一个机器人每步只能向下或向右，请计算它从格子的左上角到达右下角的路径的数字之和的最小值。例如，从下图中 3 x 3 的格子的左上角到达右下角的路径的数字之和的最小值是 8，图中数字之和最小的路径用灰色背景表示。

分析：

和面试题 98 类似，机器人从格子的左上角到达右下角需要多步，每步都可能有向下或向右两个选择。由于这个题目并没有要求列出所有的路径，而是求出路径的数字之和的最小值，也就是求最优解，因此这个问题适合应用动态规划求解。

分析确定状态转移方程：

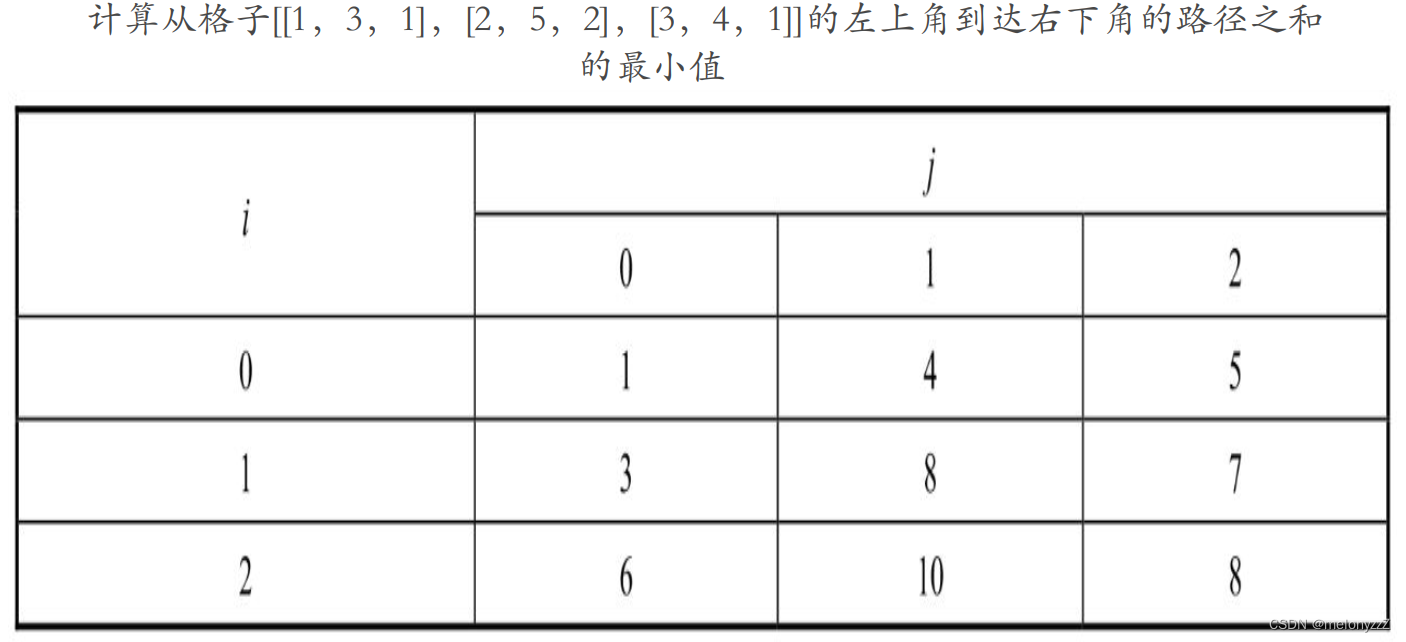
应用动态规划解决问题的关键在于找出状态转移方程。用函数 f(i, j) 表示从格子的左上角坐标为 (0, 0) 的位置（用 grid[0][0] 表示）出发到达坐标为 (i, j) 的位置（用 grid[i][j] 表示）的路径的数字之和的最小值。如果格子的大小为 m x n，那么 f(m - 1, n - 1) 就是问题的解。

class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<vector<int>> dp(m, vector<int>(n));dp[0][0] = grid[0][0];for (int j = 1; j < n; ++j){dp[0][j] = dp[0][j - 1] + grid[0][j];}
​for (int i = 1; i < m; ++i){dp[i][0] = dp[i - 1][0] + grid[i][0];for (int j = 1; j < n; ++j){dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];}}return dp[m - 1][n - 1];}
};

上述代码用二维数组 dp 保存状态转移方程的计算结果，f(i, j) 保存在 dp[i][j] 中。

上述代码的时间复杂度和空间复杂度都是 O(mn)。

优化空间效率：

由于计算 f(i, j) 时只需要用到它上面一行的 f(i - 1, j)，因此实际上只需要保存两行就可以。也就是说，创建一个只有两行的数组 dp，将 f(i, j) 保存到 dp[i % 2][j] 中即可。

还可以进一步优化空间效率，即只需要一个一维数组 dp。在计算 f(i, j) 时需要 f(i - 1, j) 的值。值得注意的是，f(i - 1, j) 在完成 f(i, j) 的计算之后再也用不到了，因此将 f(i - 1, j) 和 f(i, j) 保存到同一个数组 dp 的同一个位置 dp[j] 中。在计算 f(i, j) 之前，dp[j] 保存的是 f(i - 1, j) 的值，用 f(i - 1, j) 的值计算出 f(i, j) 的值之后，将 f(i, j) 的值保存到 dp[j] 中。虽然之前保存在 dp[j] 中的 f(i - 1, j) 的值被覆盖了，但这个值也不再需要，它被覆盖不会带来任何问题。

class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<int> dp(n);dp[0] = grid[0][0];for (int j = 1; j < n; ++j){dp[j] = dp[j - 1] + grid[0][j];}
​for (int i = 1; i < m; ++i){dp[0] += grid[i][0];for (int j = 1; j < n; ++j){dp[j] = min(dp[j], dp[j - 1]) + grid[i][j];}}return dp[n - 1];}
};

优化之后的代码的时间复杂度仍然是 O(mn)，但空间复杂度变成了 O(n)。

---

面试题 100 : 三角形中最小路径之和

题目：

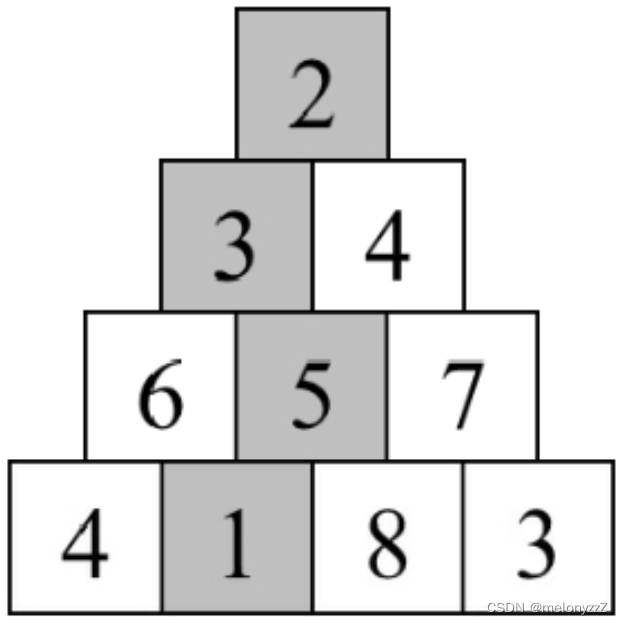
在一个由数字组成的三角形中，第 1 行有 1 个数字，第 2 行有 2 个数字，以此类推，第 n 行有 n 个数字。例如，下图是一个包含 4 行数字的三角形。如果每步只能前往下一行中相邻的数字，请计算从三角形顶部到底部的路径经过的数字之和的最小值。如下图所示，从三角形顶部到底部的路径数字之和的最小值为 11，对应的路径经过的数字用阴影表示。

分析：

可能需要用矩阵坐标来定位三角形中的数字。上图中的相邻两行数字的位置相互交错，这样很难用矩阵坐标来表示数字的位置。可以移动三角形每行的位置使它们左端对齐，如下图所示。对齐之后就能很方便地用矩阵的行坐标和列坐标来定位每个数字。如果三角形有 n 行数字，将这些行左端对齐之后就成了一个 n x n 的矩阵和左下半部分。如果三角形中某个数字在矩阵中的行号和列号分别是 i 和 j，那么 i >= j。

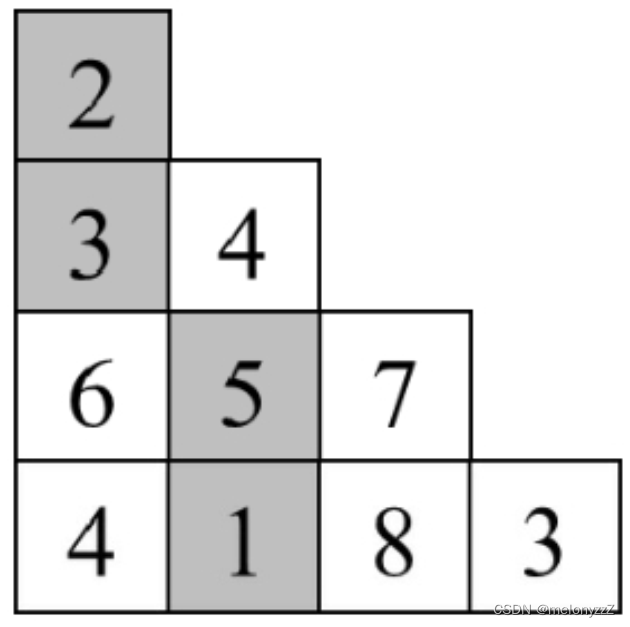
在左端对齐的三角形中，从一个数字出发，下一步要么前往下一行正下方的数字，要么前往右下方的数字。例如，在上图的三角形中从顶部的数字 2 出发，可以前往第 2 行位于它正下方的数字 3，也可以前往右下方的数字 4。

如果一个三角形有多行，那么从它的顶部到底部需要多步，而且每步都面临两个选择。例如，在上图的三角形中，从顶部数字 2 出发，下一步既可能前往第 2 行的第 1 个数字 3，也可能前往第 2 行的第 2 个数字 4。解决一个问题需要多个步骤，而且每个步骤都面临多个选择，这看起来可以用回溯法解决。但这个题目并没有要求列出从顶部到底部的所有路径，而是要求计算路径之和的最小值，也就是求最优解。因此，动态规划更适合解决这个问题。

分析确定状态转移方程：

应用动态规划解决问题的关键在于确定状态转移方程。可以用 f(i, j) 表示从三角形的顶部出发到达行号和列号分别为 i 和 j（i >= j）的位置时路径数字之和的最小值，同时用 T[i][j] 表示三角形行号和列号分别为 i 和 j 的数字。如果三角形中包含 n 行数字，那么 f(n - 1, j) 的最小值就是整个问题的最优解。

1. f(0, 0) 等于 T[0][0]。

2. 如果 j 等于 0，也就是当前到达某行的第 1 个数字。由于路径的每步都是前往正下方或右下方的数字，而此时当前位置的左上方没有数字，那么前一步一定是来自它的正上方的数字，因此 f(i, 0) 等于 f(i - 1, 0) 与 T[i][0] 之和（i > 0）。

3. 如果 i 等于 j，也就是当前到达某行的最后一个数字，此时它的正上方没有数字，前一步只能是来自它左上方的数字，因此 f(i, j) 等于 f(i - 1, j - 1) 与 T[i][j] 之和（i > 0）。

4. 如果当前行号和列号分别为 i 和 j 的位置位于某行的中间，那么前一步既可能是来自它正上方的数字（行号和列号分别为 i - 1 和 j），也可能是来自它左上方的数字（行号和列号分别为 i - 1 和 j - 1），所以 f(i, j) 等于 f(i - 1, j) 与 f(i - 1, j - 1) 的最小值再加上 T[i][j]。

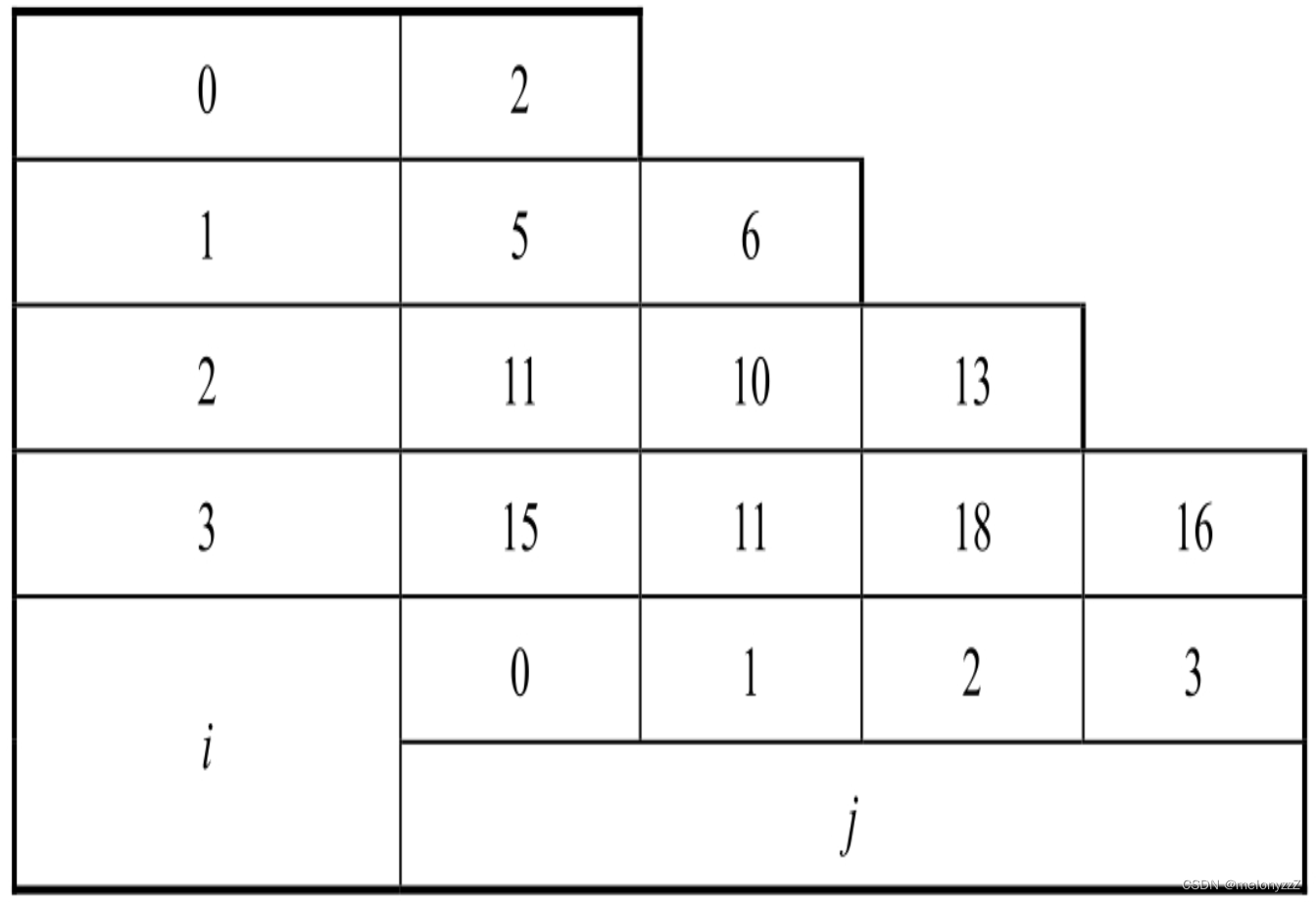
class Solution {
public:int minimumTotal(vector<vector<int>>& triangle) {int n = triangle.size();vector<vector<int>> dp(n, vector<int>(n));dp[0][0] = triangle[0][0];for (int i = 1; i < n; ++i){for (int j = 0; j <= i; ++j){dp[i][j] += triangle[i][j];if (j == 0)dp[i][j] += dp[i - 1][j];else if (j == i)dp[i][j] += dp[i - 1][j - 1];elsedp[i][j] += min(dp[i - 1][j], dp[i - 1][j - 1]);}}
​int result = INT_MAX;for (int num : dp[n - 1]){result = min(result, num);}return result;}
};

上述代码创建了一个 n x n（n 为三角形的行数）的二维数组 dp，但实际上只用到了数组的左下半部分。先用一个二重循环按照状态转移方程逐一计算 f(i, j) 的值并保存到 dp[i][j] 中，然后用一个 for 循环找出二维数组 dp 最后一行的最小值作为整个问题的最优解。

上述代码的时间复杂度和空间复杂度都是 O(n^2)。

优化空间效率：

由于计算 f(i, j) 时只需要用到它上面一行的 f(i - 1, j) 和 f(i - 1, j - 1)，因此实际上只需要保留两行就可以。也就是说，创建一个只有两行的数组 dp，将 f(i, j) 保存到 dp[i % 2][j] 中即可。

还可以考虑进一步优化空间效率，即能否只需要一个一维数组 dp。如果能够将 f(i, j) 和 f(i - 1, j) 都保存到 dp[j] 中，那么一个一维数组就可以保存所需的数据。

假设在计算 f(i, j) 之前 dp[j] 中保存的是 f(i - 1, j) 的值。在计算 f(i, j) 时需要 f(i - 1, j - 1) 和 f(i - 1, j)。在计算完 f(i, j) 之后能否用 f(i, j) 的值覆盖保存在 dp[j] 中的 f(i - 1, j) 取决于是否还需要 f(i - 1, j) 的值。

1. 如果每行按照从左到右的顺序，那么在计算完 f(i, j) 之后将计算 f(i, j + 1)，而计算 f(i, j + 1) 可能需要 f(i - 1, j) 和 f(i - 1, j + 1) 的值，也就是 f(i - 1, j) 的值在计算 f(i, j + 1) 时可能会被用到，因此在计算完 f(i, j) 之后不能将 f(i - 1, j) 的值丢掉。

2. 但计算 f(i, j) 时并不依赖同一行左侧的 f(i, j - 1)，因此并不一定要按照从左到右的顺序计算每行，按照从右到左的顺序计算也可以。如果按照从右到左的顺序，则先计算 f(i, j)，需要用到 f(i - 1, j - 1) 和 f(i - 1, j)。接下来计算 f(i, j - 1)，需要用到 f(i - 1, j - 2) 和 f(i - 1, j - 1)。计算 f(i - 1, j - 1) 并不需要用到 f(i - 1, j)。因此，按照从右到左的顺序在计算完 f(i, j) 之后，将 f(i, j) 的值保存到 dp[j] 中并替换 f(i - 1, j) 的值，并且不会带来任何问题，因此 f(i - 1, j) 的值以后就不再需要。

class Solution {
public:int minimumTotal(vector<vector<int>>& triangle) {int n = triangle.size();vector<int> dp(n);dp[0] = triangle[0][0];
​for (int i = 1; i < n; ++i){for (int j = i; j >= 0; --j){if (j == i)dp[j] = dp[j - 1] + triangle[i][j];else if (j == 0)dp[j] += triangle[i][j];elsedp[j] = min(dp[j - 1], dp[j]) + triangle[i][j];}}
​int result = INT_MAX;for (int num : dp){result = min(result, num);}return result;}
};

上述代码的时间复杂度仍然是 O(n^2)，但空间复杂度变成了 O(n)。