leecode 331 |验证二叉树的前序序列化 | gdb 调试找bug
计算的本质是数据的计算
数据的计算需要采用格式化的存储,
规则的数据结果,可以快速的按照指定要求存储数据
这里就不得不说二叉树了,二叉树应用场景真的很多
本题讲的是,验证二叉树的前序序列化
换言之,不采用建立树的结构体去判断给定的数据能否构建前序二叉树
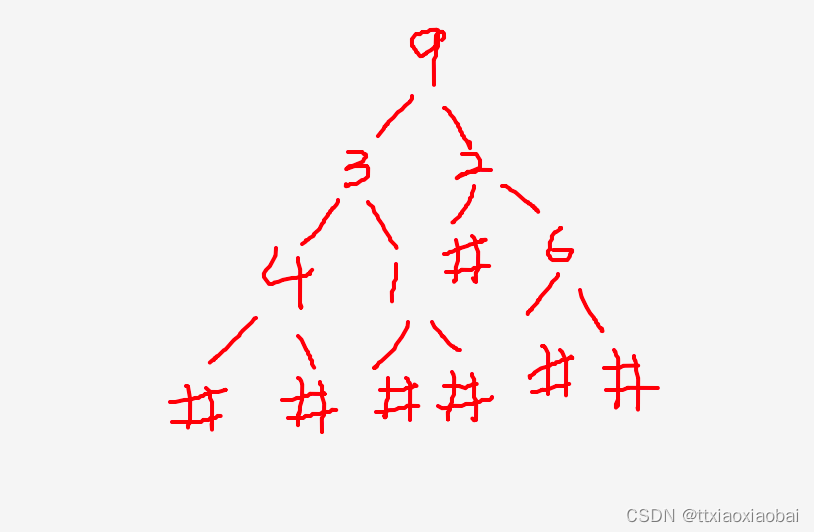
比如前序二叉树的数据为: “9, 3, 4, #, #, 1, #, #, 2, #, 6, #, #”
就这样,给一字符串,包含整数、‘,’, '#'这三种数据类型
然后这个给定的字符串是二叉树的前序序列,现在需要你判定它是不是真的前序序列化(真的前序序列化是可以构建先序二叉树的)
注意哈 # 表示 空节点
//思路,用栈记录槽
//槽 是节点可存储节点的数量。
//栈顶记录 存储 当前节点
// 如果当前节点为空 槽要 -1 (也就是 栈顶 -1 )(如果栈顶减为 0,退栈)
//注意:在遍历的过程中,栈顶槽的大小是这样确定的,如果遍历到的节点为空节点,stk.top() -=1; 如果遍历到的节点非空,那么stk.top() -= 1; stk.push(2); //完成当前节点 槽 的更新,再在栈push 两个槽
//如果栈为空,但是还没有遍历结束 那证明这个序列构建不了先序二叉树
#include <stack>
#include <string>
#include <iostream>bool solution(std::string &str){std::stack<int> stk;int n = str.size();int i = 0;//最开始,如栈根节点stk.push(1);while(i < n){// 栈为空 直接 return falseif(stk.empty()){return false; //line 18}// 如果是 ‘,’ i++if(str[i] == ','){i++; // line 24}else if(str[i] == '#'){// 如果是空节点 当前槽 -1stk.top() -= 1; // line 28if(!stk.top()){stk.pop();}// 别忘了 还要 i++ 待会会讲我怎么gdb 调试找到这个bug 的(我测试的时候,忘了这块,然后调试定位到这个问题了)i++;}else{// 这里的都是非零节点的处理while(i < n && str[i] != ',' && str[i] != '#'){i++;}stk.top() -= 1; // line 36if(!stk.top()){stk.pop();}stk.push(2);}}return stk.emptu();
}
int main(){std::string str = "9,3,4,#,#,1,#,#,2,#,6,#,#";if(solution(str)){std::cout<<" this is true"<<std::endl;}else{std::cout<<" this is false"<<std::endl;}return 0;
}
说明一下 上面的注释 //line xxx 是为了写这篇博客方便 定位这行的位置,注意区分
再说一说调试,因为我运行,输入正确的前序序列返回的也是错误的,后面后就gdb 调试
g++ test_331.cpp -g
gdb a.out
b 18
b 24
b 28
b 36打了四个断点
r
然后单点调试
c
发现一直在 分支 ‘#’ 这块走,
我们定义的是,如果节点为空,槽 - 1
但是这里会一直跑,因为,当栈顶为空,会退栈,把栈下面的第一个元素移成栈顶,接着循环(如果栈 无穷,那在这里死循环 ,因为 i 这个计数器一直没有更新
可以打印 i
p i
好了 ,大概就是这样了。
EOF
相关文章:
leecode 331 |验证二叉树的前序序列化 | gdb 调试找bug
计算的本质是数据的计算 数据的计算需要采用格式化的存储, 规则的数据结果,可以快速的按照指定要求存储数据 这里就不得不说二叉树了,二叉树应用场景真的很多 本题讲的是,验证二叉树的前序序列化 换言之,不采用建立树的…...

服务器安全事件应急响应排查方法
针对服务器操作系统的安全事件也非常多的。攻击方式主要是弱口令攻击、远程溢出攻击及其他应用漏洞攻击等。分析安全事件,找到入侵源,修复漏洞,总结经验,避免再次出现安全事件,以下是参考网络上文章,总结的…...

数码视讯Q7盒子刷armbian或emuelec的一些坑
首先,我手头的盒子是nand存储的,如果是emmc的,会省事很多…… 以下很多结论是我的推测,不一定准确。 1,原装安卓系统不支持SD卡或U盘启动,所以只能进uboot修改启动参数 2,原装安卓系统应该是…...

2_2.Linux中的远程登录服务
# 一.Openssh的功能 # 1.sshd服务的用途# #作用:可以实现通过网络在远程主机中开启安全shell的操作 Secure SHell >ssh ##客户端 Secure SHell daemon >sshd ##服务端 2.安装包# openssh-server 3.主配置文件# /etc/ssh/sshd_conf 4.…...
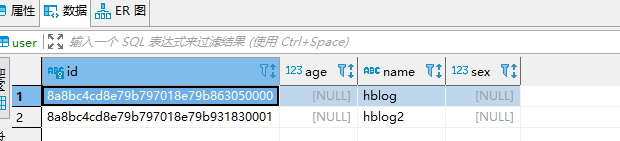
Spring Boot集成JPA快速入门demo
1.JPA介绍 JPA (Java Persistence API) 是 Sun 官方提出的 Java 持久化规范。它为 Java 开发人员提供了一种对象/关联映射工具来管理 Java 应用中的关系数据。他的出现主要是为了简化现有的持久化开发工作和整合 ORM 技术,结束现在 Hibernate,TopLink&am…...
深度学习理解及学习推荐(持续更新)
主推YouTuBe和Bilibili 深度学习博主推荐: Umar Jamil - YouTubehttps://www.youtube.com/umarjamilai StatQuest with Josh Starmer - YouTubehttps://www.youtube.com/statquest RNN Illustrated Guide to Recurrent Neural Networks: Understanding the Int…...

【C语言】贪吃蛇【附源码】
欢迎来到英杰社区https://bbs.csdn.net/topics/617804998 一、游戏说明: 一个基于C语言链表开发的贪吃蛇游戏: 1. 按方向键上下左右,可以实现蛇移动方向的改变。 2. 短时间长按方向键上下左右其中之一,可实现蛇向该方向的短时间…...
【技巧】压缩文件如何设置“自动加密”?
很多人会在压缩文件的时候,同时设置密码,以此保护私密文件。如果经常需要压缩文件并设置密码,不妨使用解压缩软件的“自动加密”功能,更省时省力。 下面介绍WinRAR解压缩软件的两种“自动加密”的方法,一起来看看吧&a…...

内网穿透时报错【Bad Request This combination of host and port requires TLS.】的原因
目录 前言:介绍一下内网穿透 1.内网直接https访问(可以正常访问) 程序配置的证书 2.内网穿透后,通过外网访问 3.原因 4.内网非https的Web应用,使用https后,也变成了https访问 5.题外话 感觉自己的web应用配置了…...
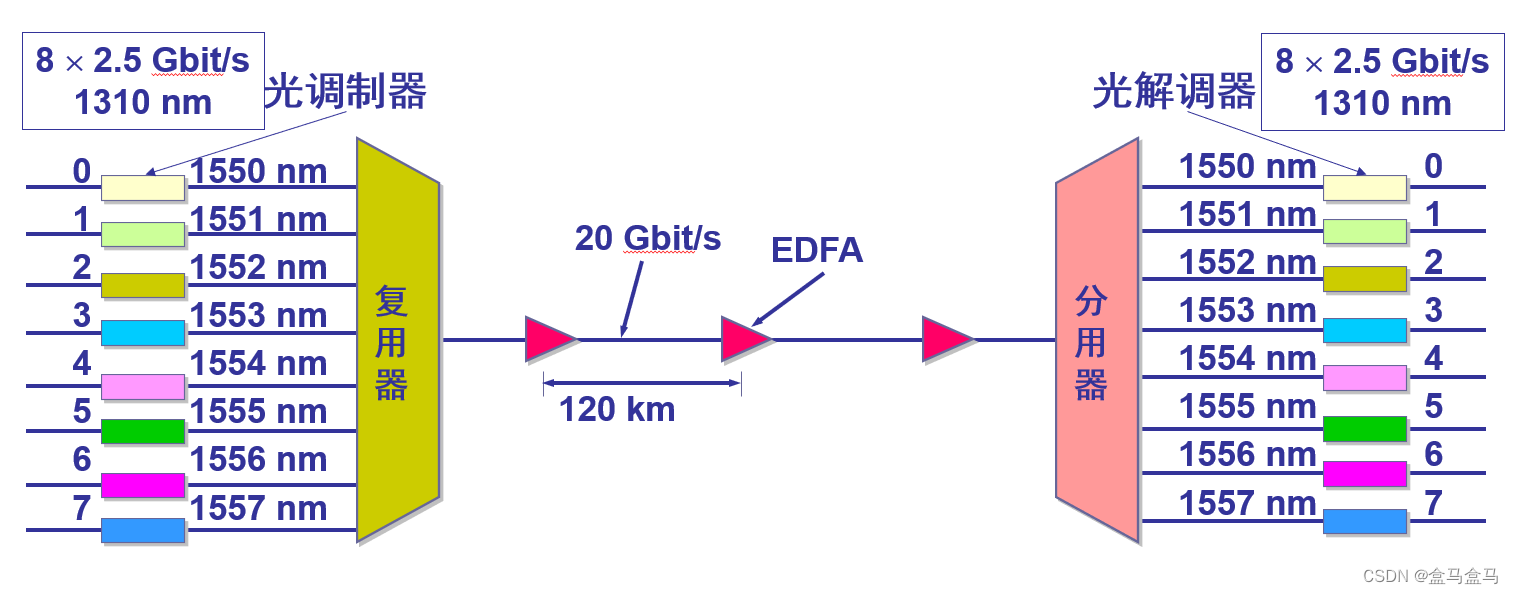
计算机网络:物理层 - 信道复用
计算机网络:物理层 - 信道复用 频分复用时分复用统计时分复用波分复用码分复用 计算机网络中,用户之间通过信道进行通信,但是信道是有限的,想要提高网络的效率,就需要提高信道的利用效率。因此计算机网络中普遍采用信道…...

【算法集训】基础算法:滑动窗口
定义一个快慢指针,用于截取数组中某一段信息。同时可以改变快慢指针的值来获取结果,这个过程比较像滑动。 1493. 删掉一个元素以后全为 1 的最长子数组 定义快慢指针快指针先走,如果到了第二个0上的时候。前面1的个数就是fast - slow - 1&a…...
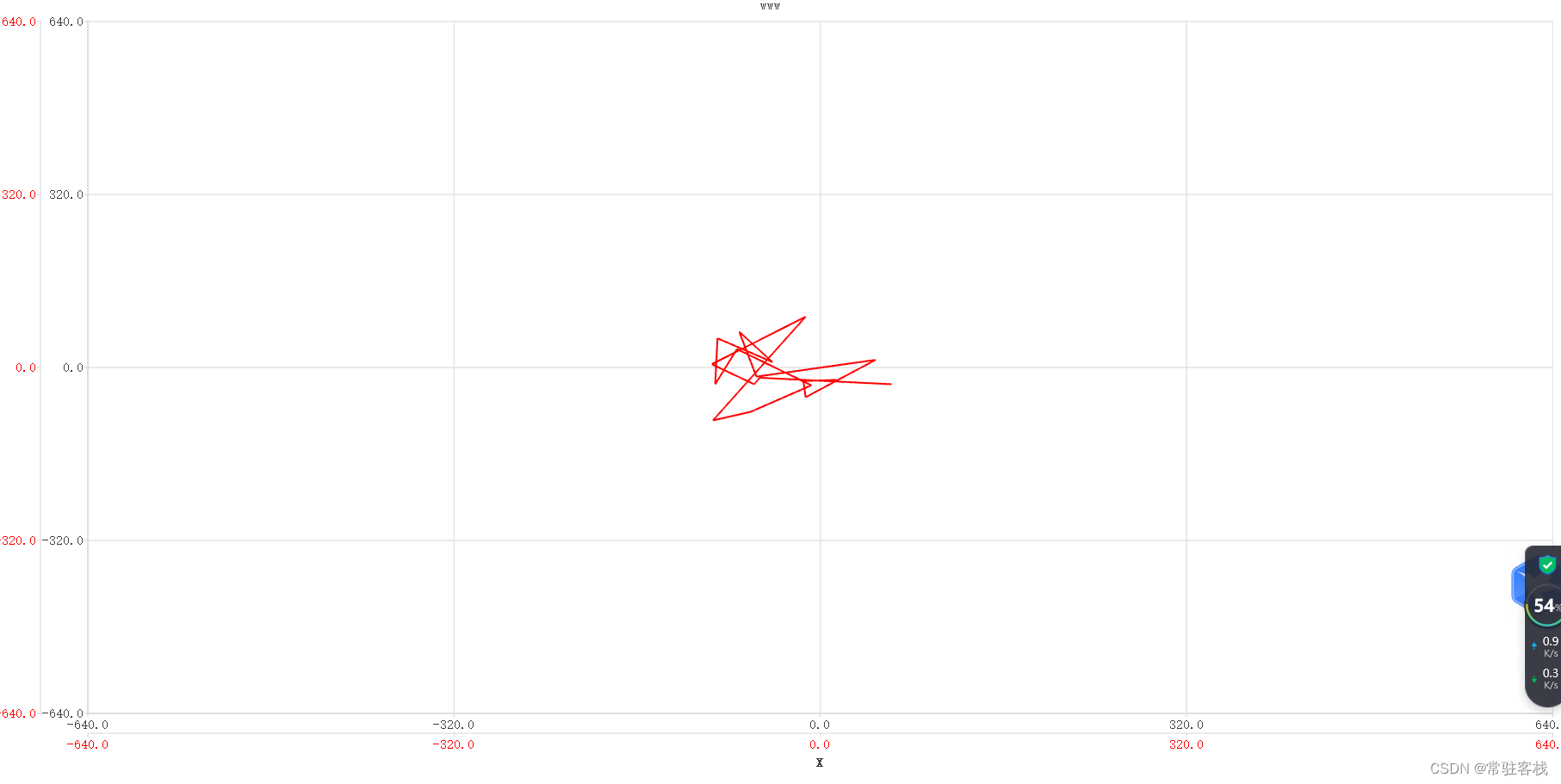
QT 二维坐标系显示坐标点及点与点的连线-通过定时器自动添加随机数据点
QT 二维坐标系显示坐标点及点与点的连线-通过定时器自动添加随机数据点 功能介绍头文件C文件运行过程 功能介绍 上面的代码实现了一个简单的 Qt 应用程序,其功能包括: 创建一个 MainWindow 类,继承自 QMainWindow,作为应用程序的…...
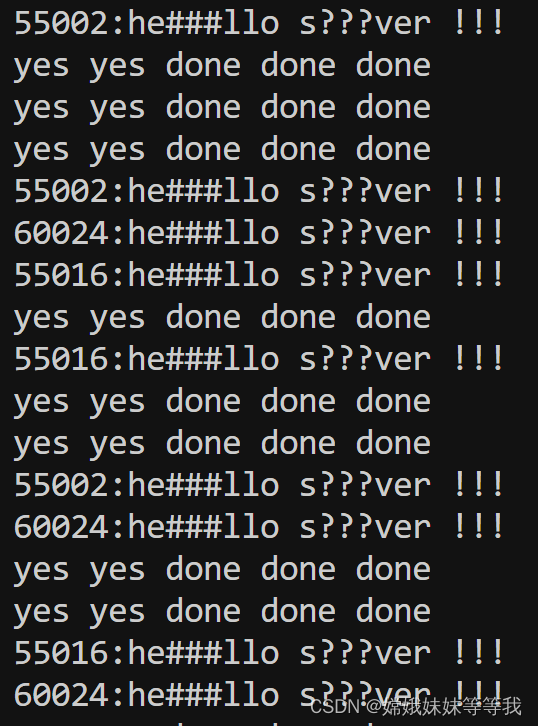
C语言TCP服务器模型 : select + 多线程与双循环单线程阻塞服务器的比较
观察到的实验现象: 启动三个客户端: 使用双循环阻塞服务器:只能accept后等待收发,同时只能与一个客户端建立连接,必须等已连接的客户端多次收发 明确断开后才能与下个客户端连接 使用IO多路复用select:可以同时接收所有的连接请求,并且连接状态一直是存活的,直到客户端关闭连…...
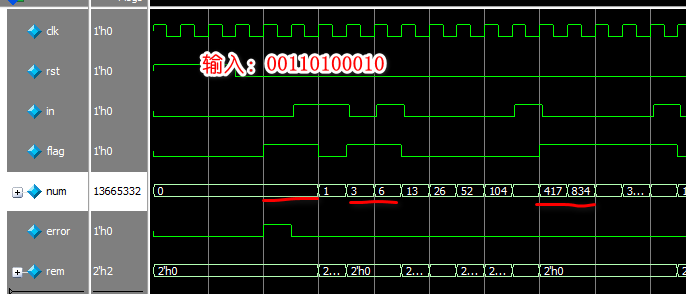
【数字IC/FPGA】手撕代码:模3检测器(判断输入序列能否被3整除)
今天我们来手撕一个常见的笔试题,使用的方法是三段式Moore状态机。 题目描述: 输入端口是串行的1bit数据,每个时钟周期进来一位新数据后,实时检查当前序列是否能整除3,若能则输出1,否则输出0。 例如&#…...

最小可行产品需要最小可行架构——可持续架构(三)
前言 最小可行产品(MVP)的概念可以帮助团队专注于尽快交付他们认为对客户最有价值的东西,以便在投入大量时间和资源之前迅速、廉价地评估产品的市场规模。MVP不仅需要考虑产品的市场可行性,还需要考虑其技术可行性,以…...

笔记: 数据结构与算法--时间复杂度二分查找数组
算法复杂度 不依赖于环境因素事前分析法 计算最坏情况的时间复杂度每一条语句的执行时间都按照t来计算 时间复杂度 大O表示法 n 数据量 ; f(n) 实际的执行条数当存在一个n0 , 使得 n > n0,并且 c * g(n) 恒> f(n) : 渐进上界(算法最坏的情况)那么f(n)的时间复杂度 …...

AI绘画教程:Midjourney使用方法与技巧从入门到精通
文章目录 一、《AI绘画教程:Midjourney使用方法与技巧从入门到精通》二、内容介绍三、作者介绍🌤️粉丝福利 一、《AI绘画教程:Midjourney使用方法与技巧从入门到精通》 一本书读懂Midjourney绘画,让创意更简单,让设计…...

Spring-事务管理
1、事务管理 1.1、回滚方式 默认回滚方式:发生运行异常时异常和error时回滚,发生受查(编译)异常时提交。不过,对于受查异常,程序员也可以手工设置其回滚方式 1.2、事务定义接口 1.2.1、事务隔离级别常量 这些常量…...
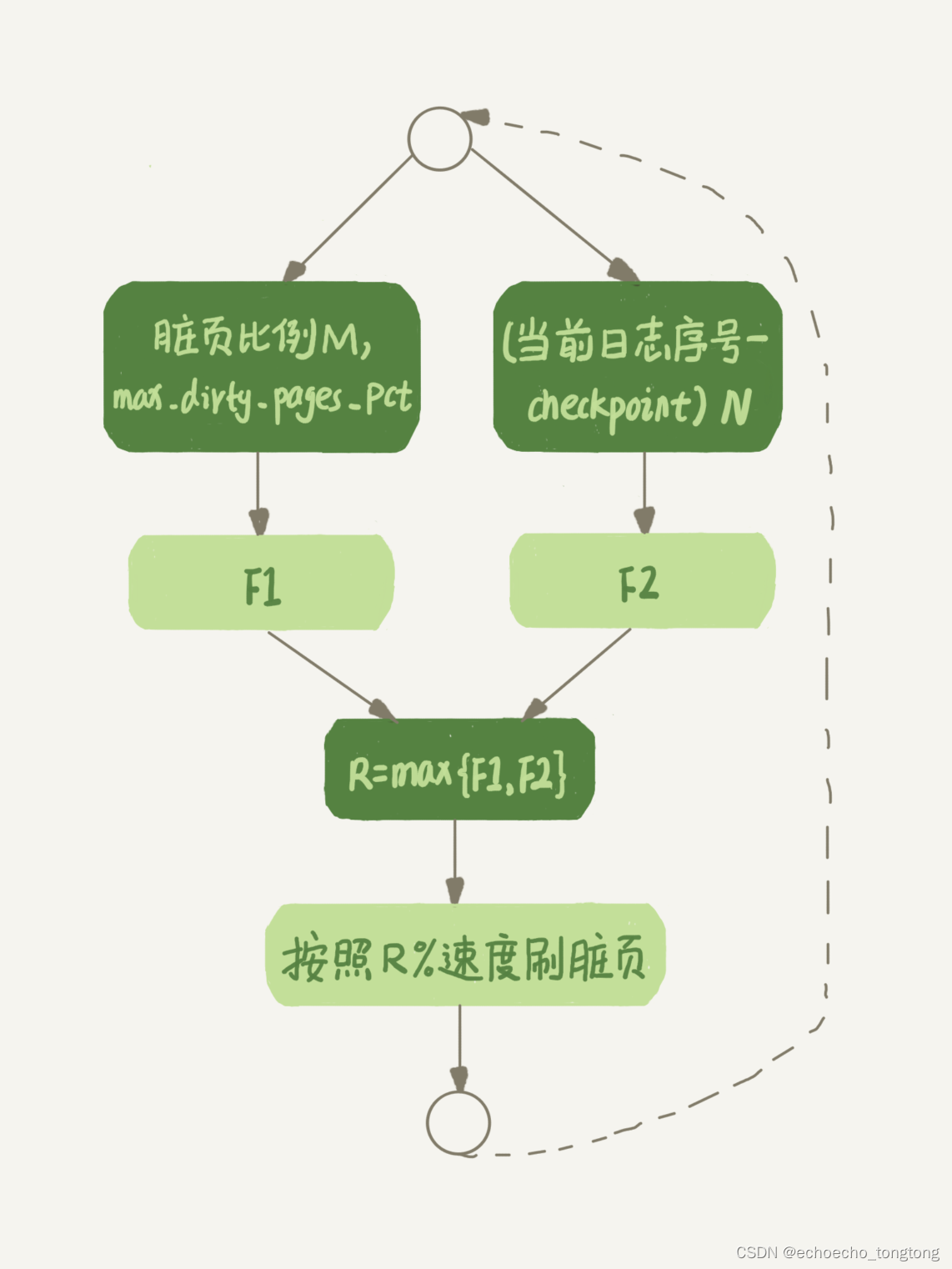
MySql实战--为什么我的MySQL会“抖”一下
时的工作中,不知道你有没有遇到过这样的场景,一条SQL语句,正常执行的时候特别快,但是有时也不知道怎么回事,它就会变得特别慢,并且这样的场景很难复现,它不只随机,而且持续时间还很短…...
【蓝桥杯第十三届省赛B】(部分详解)
九进制转十进制 #include <iostream> #include<math.h> using namespace std; int main() {cout << 2*pow(9,3)0*pow(9,2)2*pow(9,1)2*pow(9,0) << endl;return 0; }顺子日期 #include <iostream> using namespace std; int main() {// 请在此…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
