笔记: 数据结构与算法--时间复杂度二分查找数组
算法复杂度
- 不依赖于环境因素
- 事前分析法
- 计算最坏情况的时间复杂度
- 每一条语句的执行时间都按照t来计算
时间复杂度
- 大O表示法
- n = 数据量 ; f(n) = 实际的执行条数
- 当存在一个n0 , 使得 n > n0,并且 c * g(n) 恒> f(n) : 渐进上界(算法最坏的情况)
- 那么f(n)的时间复杂度 => O(g(n))
- 大O表示法
- f(n)中的常数量省略
- f(n)中较低次幂省略
- log2(n) => log(n)
- 常见的表示
- O(1) > O(log(n)) >> O(n) > O(nlog(n)) >> O(n2) > O(2^n) >> O(n!)
空间复杂度
- 除原始参数以外,额外空间成本
二分查找
基础版
-
步骤
- 有序数组A , 目标值target
- 左右索引值 : i = 0 , j = n - 1;
- 判断 i > j => 结束查找,没找到
- 中间索引 m = ( i + j) / 2 : 整形自动向下取整
- 判断 m > target : j = m -1; -> 跳到第三步继续执行
- 判断 m < target : i = m + 1; -> 跳到第三步继续执行
- 判断 m = target : 得到结果结束程序,返回索引值
-
代码如下
/*** 编写二分查找方法* @param A : 有序数组a* @param target : 目标查找值* @return 返回索引值*/public static int binarySearchBasic(int[] A, int target) {// 定义左右指针int i = 0, j = A.length - 1;// 定义循环条件while (i <= j) {// 定义中间指针m// int m = (i + j) / 2; int m = (i + j) >>> 1; // 判断A[m] 值 与 target值if (target < A[m]){// 中间值大 : 指针[m , j]中的值都会比target值大j = m - 1;} else if (A[m] < target){// 中间值小 : 指针[i , m]中的值都会比target值小i = m + 1;} else {// A[m] == target: 得到结果,结束循环,返回mreturn m;}}//i > j : 结束循环return -1; // 结束循环,返回-1} -
问题一 : 代码while循环中为什么是i <= j , 而不是 i < j ?
答 : 首先 代码return -1; 本身表示的就是在 i>j 的情况下结束,没有找到,返回-1; , 那么相反对应的循环内就应该为 i <= j
其次, while(i < j ) 表示的是 只有i,j中间的m会参与比较 ; 而while(i <= j) : 表示 i , j所指向的元素 也会参与比较. 当i == j 的时候, m = i = j = (i + j) /2
-
问题二: 代码 int m = (i + j) / 2; 是否有问题?
答: 有问题.
假设 j 的值为整数类型最大值 (Integer.MAX_VALUE - 1) , 并且target值在数组的右侧 (target > A[m]) , 那么我们就需要将 索引i 的值调到m的右侧
即 : i = (i + j) /2 + 1; j = 整数类型最大值 = Integer.MAX_VALUE - 1;
那么根据Java int类型的特性, Java二进制首位为符号位,则会导致下一次进行 m = (i + j) / 2 的时候,使m成为负数
解决办法: 无符号右移运算符 数字 >>> 位数n
在二进制中,二进制码整体向右平移指定位数n就相当于n / 2n , 数字 >>> 1 => 数字 / 2运算取整
改动版
-
步骤
- 让右指针作为边界,必须不参与比较运算
- 循环不能有i=j的情况,如果i=j的话,则会造成m = i = j = (i + j) / 2 , 则不符合第一点j不参与比较运算的条件
- 当m指针所对应的值 > target值时,让j指针=m , 因为m指针对应的值已经参与过比较,并且肯定不等于target值,可作为边界不参与比较运算.
- 如果还是j = m - 1情况, m - 1的指针存在这等于target的可能,于第一点让j作为边界条件不服.
- 并且,当j= m - 1 , 如果要查找的target值不在数组A中时,会出现死循环的情况
-
代码如下
public static int binarySearchAlter(int[] A, int target) {// 改动一: 其中右指针j作为边界, 必须不参与运算比较int i = 0, j = A.length;// 定义循环条件 , 改动二: 由于不让j指针值参与比较, 故不需要i=j的情况,当i=j时,j被带着参与了比较,当target值不是数组值的时候,会导致死循环的情况while (i < j) {int m = (i + j) >>> 1;if (target < A[m]) {// 改动三: j作为边界,不参与比较.故当判断出来target值在m指针左侧时,m指针对应值已经判断过了,不可能和target相等,让j=m,及让j作为一个不可能相等的边界使用j = m;} else if (A[m] < target) {i = m + 1;} else {return m;}}return -1;}
平衡版
-
代码如下
/*** 二分查找平衡版** @param A : 有序数组a* @param target : 目标查找值* @return 返回索引值*/public static int binarySearchBalance(int[] A, int target) {// 定义左右边界,左边i指针对应的值可能target , 右指针j作为边界, 必须不参与运算比较int i = 0, j = A.length;// 定义循环条件 , 目的为缩小比较范围,将最后比较功能放到循环以外// 由i < j => 0 < j - i 改为 1 < j - i; 表示[i , j]区间内待比较的个数是否有1个以上while (1 < j - i) {// 定义中间索引int m = (i + j) >>> 1;if (target < A[m]) {// j作为右边界,不参与比较.故当判断出来target值在m指针左侧时,m指针对应值已经判断过了,不可能和target相等,让j=m,及让j作为一个不可能相等的边界使用j = m;} else {// 及 A[m] <= target的情况,及 i指针对应的值是有可能为target结果的i = m;}}// 将缩减范围后剩余的一个索引i所对应的值与target进行比较if (A[i] == target){return i;} else {return -1;}}
二分查找-Java版源码
- 通过Arrays.binarySearch(int[] arr, int key);方法调用
/*** Searches the specified array of ints for the specified value using the* binary search algorithm. The array must be sorted (as* by the {@link #sort(int[])} method) prior to making this call. If it* is not sorted, the results are undefined. If the array contains* multiple elements with the specified value, there is no guarantee which* one will be found.** @param a the array to be searched* @param key the value to be searched for* @return index of the search key, if it is contained in the array;* otherwise, <code>(-(<i>insertion point</i>) - 1)</code>. The* <i>insertion point</i> is defined as the point at which the* key would be inserted into the array: the index of the first* element greater than the key, or {@code a.length} if all* elements in the array are less than the specified key. Note* that this guarantees that the return value will be >= 0 if* and only if the key is found.*/public static int binarySearch(int[] a, int key) {return binarySearch0(a, 0, a.length, key);}// Like public version, but without range checks.private static int binarySearch0(int[] a, int fromIndex, int toIndex,int key) {int low = fromIndex;int high = toIndex - 1;while (low <= high) {int mid = (low + high) >>> 1;int midVal = a[mid];if (midVal < key)low = mid + 1;else if (midVal > key)high = mid - 1;elsereturn mid; // key found}return -(low + 1); // key not found.}
二分查找对于重复元素查找的处理
获取重复最左侧索引值
-
步骤
- 添加一个结果变量索引值,用来存储当m索引值与target相等时,存储m索引值 ,
- 当相等时,j继续缩小边界,程序继续直到程序结束,获取最左侧结果
- i > j : 结束循环 , 返回结果索引值
-
代码如下
public static int binarySearchLeftMost(int[] A, int target) {// 定义左右指针int i = 0, j = A.length - 1;// 定义结果变量索引值int resIndex = -1;// 定义循环条件while (i <= j) {// 定义中间指针mint m = (i + j) / 2;// 判断A[m] 值 与 target值if (target < A[m]){// 中间值大 : 指针[m , j]中的值都会比target值大j = m - 1;} else if (A[m] < target){// 中间值小 : 指针[i , m]中的值都会比target值小i = m + 1;} else {// A[m] == target: 将结果存储到结果索引值中, 并将右侧边界缩小,继续进行程序,直到程序结束,获取最左侧结果resIndex = m;j = m - 1;}}//i > j : 结束循环 , 返回结果索引值return resIndex;} -
获取重复最右侧索引值 : 将上放代码第20行 j = m - 1; => 改为 i = m + 1; 即可
修改返回值意义
-
获取<= 索引值 最靠右的索引值结果 , 代码如下:
public static int binarySearchRightMost1(int[] A, int target) {// 定义左右指针int i = 0, j = A.length - 1;// 定义循环条件while (i <= j) {// 定义中间指针mint m = (i + j) / 2;// 判断A[m] 值 与 target值if (target < A[m]) { j = m - 1;} else {i = m + 1;}}//返回 <= 索引值 最靠右的索引值结果return i - 1;} -
获取 >= target 最靠左的索引位置 , 代码如下:
public static int binarySearchLeftMost1(int[] A, int target) {// 定义左右指针int i = 0, j = A.length - 1;// 定义循环条件while (i <= j) {// 定义中间指针mint m = (i + j) / 2;// 判断A[m] 值 与 target值if (target <= A[m]) {// 中间值>= targetj = m - 1;} else {// 中间值小 : 指针[i , m]中的值都会比target值小i = m + 1;}}//返回 >= target最靠左的索引位置return i;}
应用
- leftMost() :
- 求排名 leftMost() + 1 ;
- 求前任 leftMost() - 1 ;
- rightMost() :
- 求后任 rightMost + 1;
- 最近邻居问题
- 求前任 , 求后任
- 计算两个值 离 本值 更小的
- 范围查询
- x < n : [0 , leftMost(n) - 1]
- x <= n : [0 , rightMost(n)]
- x > n : [rightMost(n) + 1 , ∞]
- x >= n : [leftMost(n) , ∞]
- n <= x <= m : [leftMost(n) , rightMost(m)]
- n < x < m : [rightMost(n) + 1 . leftMost(m) - 1]
性能
- 时间复杂度最坏情况 : O(log(n))
- 空间复杂度 : O(1)
数组
-
连续存储
- -> 故可以通过索引值计算地址
- 公式 : 索引位置 + i * 字节数
-
随机访问时间复杂度: O(1)
-
动态数组类需要三个东西
- 数组容量
- 数组逻辑大小 : 就是数组实际存了几个值
- 静态数组
-
给数组添加元素
-
在末尾添加元素 => 给数组size位置上添加元素 -> 即调用下面方法
-
给数组指定位置添加元素
- 将数组指定位置后的元素后移
- 插入元素到指定位置上
-
插入删除的时间复杂度: O(n)
-
代码如下:
// 给数组添加元素 => 给数组size位置上添加元素private void add(int element){ // arrs[size] = element; // size++;addAppoint(size, element);}// 给数组指定位置添加元素private void addAppoint(int index , int element){if (index >= 0 && index < size){System.arraycopy(arrs, index, arrs, index + 1, size - index);}arrs[index] = element;size++;}
-
-
当数组存储元素达到容量上限,需要考虑数组扩容问题
-
每次添加元素的时候,判断size和capacity
- 定义一个新数组,容量大小是旧数组的1.5倍或两倍
- 将旧数组的数据复制到新数组中
- 将新数组的引用值 赋值 给旧数组
-
使用懒惰初始化思想优化代码
-
代码如下:
private void checkArrsCapacity() {if (size == 0) {arrs = new int[capacity];} else if (capacity == size) {capacity += capacity >> 1; // 扩大数组容量int[] newArrs = new int[capacity];System.arraycopy(arrs, 0, newArrs, 0, size);arrs = newArrs;}}@Test@DisplayName("测试扩容")public void test5() {DynamicArray dynamicArray = new DynamicArray();for (int i = 0; i < 9; i++) {dynamicArray.add(i + 1);}assertIterableEquals(List.of(1, 2, 3, 4, 5, 6, 7, 8, 9), dynamicArray);}
-
-
给动态数组遍历的三种方式
-
使用Consumer函数式接口,实现遍历
// 动态数组的遍历 , 使用Comsumer函数式接口实现public void foreach(Consumer<Integer> consumer){for (int i = 0; i < size; i++) {consumer.accept(arrs[i]);}}@Testpublic void test3() {DynamicArray dynamicArray = new DynamicArray();dynamicArray.add(1);dynamicArray.add(2);dynamicArray.add(3);dynamicArray.foreach(System.out::println);} -
使用迭代器实现遍历
@Overridepublic Iterator<Integer> iterator() {return new Iterator<Integer>() {int i = 0;@Overridepublic boolean hasNext() {return i < size;}@Overridepublic Integer next() {return arrs[i++];}};}@Testpublic void test2() {DynamicArray dynamicArray = new DynamicArray();dynamicArray.add(1);dynamicArray.add(2);dynamicArray.add(3);for (Integer element : dynamicArray) {System.out.println(element);}} -
使用stream流实现遍历
// 动态数组的遍历: 使用stream流实现public IntStream stream(){return IntStream.of(Arrays.copyOfRange(arrs, 0, size));}@Testpublic void test1() {DynamicArray dynamicArray = new DynamicArray();dynamicArray.add(1);dynamicArray.add(2);dynamicArray.add(3);dynamicArray.stream().forEach(System.out::println);}
-
-
动态数组的删除
- 使用system.arraycopy方法, 将要删除指针后的元素向前移动一位
- 插入删除: O(n)
public int remove(int index) {int removeNum = arrs[index]; // 返回删除数据if (index < size - 1) {System.arraycopy(arrs, index + 1, arrs, index, size - index - 1);}size--;return removeNum;}// 使用断言进行测试@Test@DisplayName("测试删除")public void test4() {DynamicArray dynamicArray = new DynamicArray();dynamicArray.add(1);dynamicArray.add(2);dynamicArray.add(3);dynamicArray.add(4);dynamicArray.add(5);int remove = dynamicArray.remove(3); // System.out.println("remove = " + remove);assertEquals(4 , remove);// 遍历剩余数组元素// dynamicArray.foreach(System.out::println);assertIterableEquals(List.of(1,2,3,5), dynamicArray);}
相关文章:

笔记: 数据结构与算法--时间复杂度二分查找数组
算法复杂度 不依赖于环境因素事前分析法 计算最坏情况的时间复杂度每一条语句的执行时间都按照t来计算 时间复杂度 大O表示法 n 数据量 ; f(n) 实际的执行条数当存在一个n0 , 使得 n > n0,并且 c * g(n) 恒> f(n) : 渐进上界(算法最坏的情况)那么f(n)的时间复杂度 …...

AI绘画教程:Midjourney使用方法与技巧从入门到精通
文章目录 一、《AI绘画教程:Midjourney使用方法与技巧从入门到精通》二、内容介绍三、作者介绍🌤️粉丝福利 一、《AI绘画教程:Midjourney使用方法与技巧从入门到精通》 一本书读懂Midjourney绘画,让创意更简单,让设计…...

Spring-事务管理
1、事务管理 1.1、回滚方式 默认回滚方式:发生运行异常时异常和error时回滚,发生受查(编译)异常时提交。不过,对于受查异常,程序员也可以手工设置其回滚方式 1.2、事务定义接口 1.2.1、事务隔离级别常量 这些常量…...
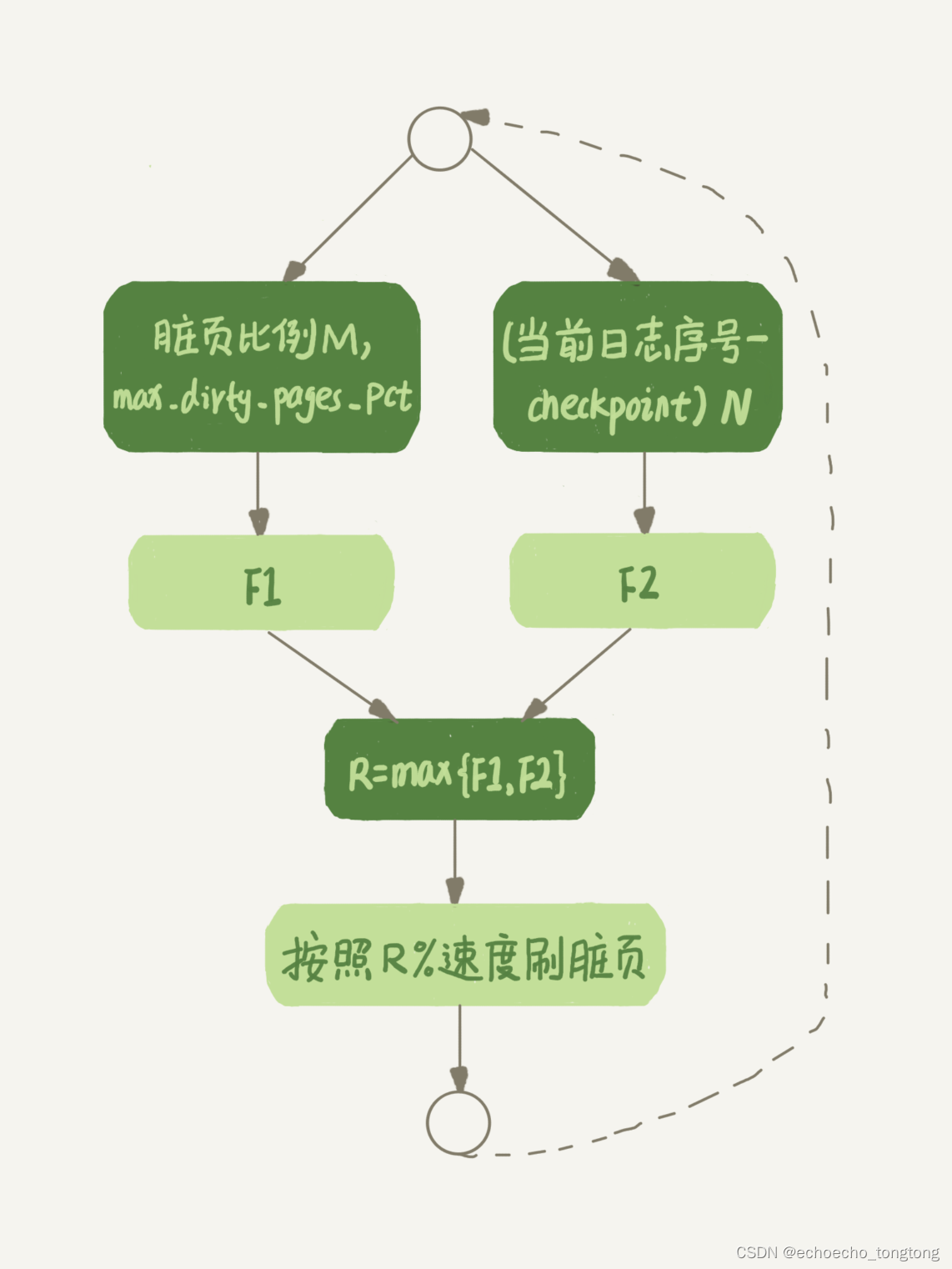
MySql实战--为什么我的MySQL会“抖”一下
时的工作中,不知道你有没有遇到过这样的场景,一条SQL语句,正常执行的时候特别快,但是有时也不知道怎么回事,它就会变得特别慢,并且这样的场景很难复现,它不只随机,而且持续时间还很短…...
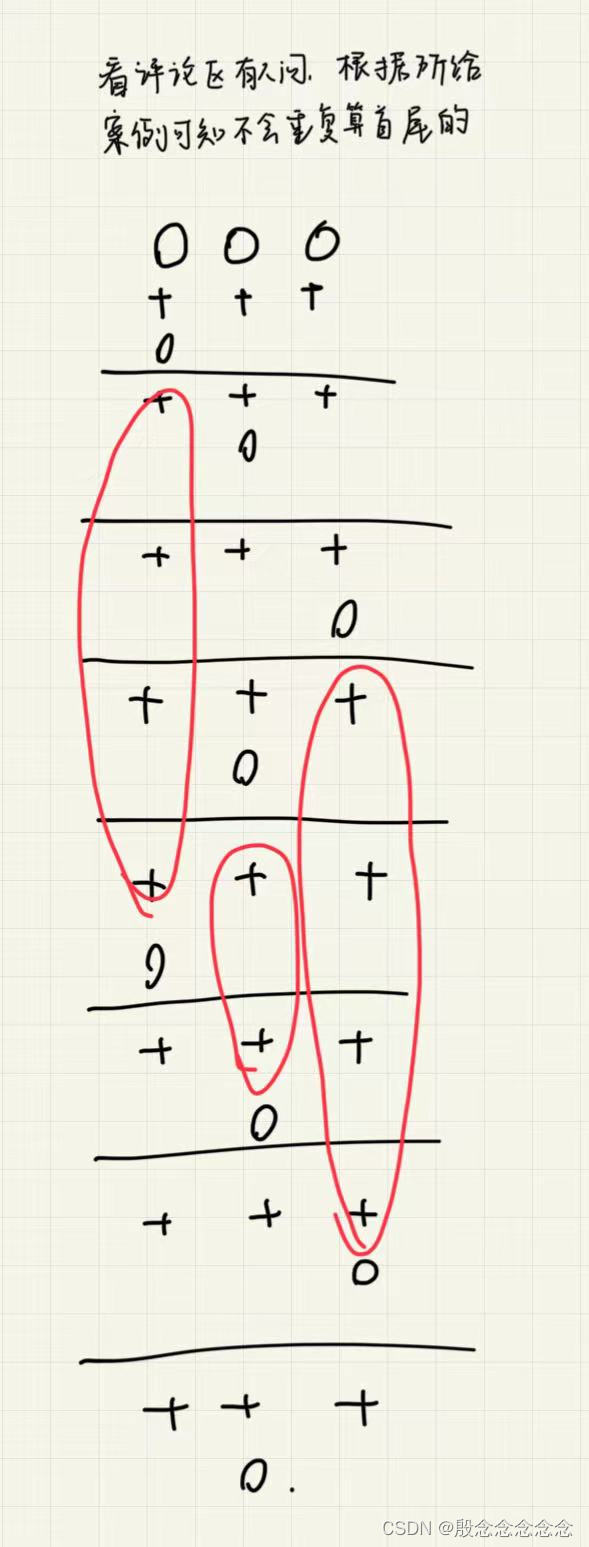
【蓝桥杯第十三届省赛B】(部分详解)
九进制转十进制 #include <iostream> #include<math.h> using namespace std; int main() {cout << 2*pow(9,3)0*pow(9,2)2*pow(9,1)2*pow(9,0) << endl;return 0; }顺子日期 #include <iostream> using namespace std; int main() {// 请在此…...
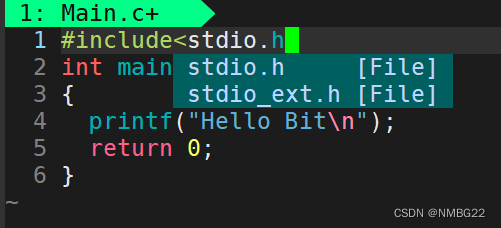
[linux初阶][vim-gcc-gdb] OneCharter: vim编辑器
一.vim编辑器基础 目录 一.vim编辑器基础 ①.vim的语法 ②vim的三种模式 ③三种模式的基本切换 ④各个模式下的一些操作 二.配置vim环境 ①手动配置(不推荐) ②自动配置(推荐) vim是vi的升级版,包含了更加丰富的功能. ①.vim的语法 vim [文件名] ②vim的三种模式 命令…...

【Lazy ORM 框架学习】
Gitee 点赞关注不迷路 项目地址 快速入门 模块所属层级描述快照版本正式版本wu-database-lazy-lambdalambda针对不同数据源wu-database-lazy-orm-coreorm 核心orm核心处理wu-database-lazy-sqlsql核心处理成处理sql解析、sql执行、sql映射wu-elasticsearch-starterESESwu-hb…...

安科瑞路灯安全用电云平台解决方案【电不起火、电不伤人】
背景介绍 近年来 ,随着城市规模的不断扩大 ,路灯事业蓬勃发展。但有的地方因为观念、技术、管理等方面不完善 ,由此引发了一系列安全问题。路灯点多面广 ,一旦漏电就极容易造成严重的人身安全事故。不仅给受害者家庭带来痛苦 &am…...
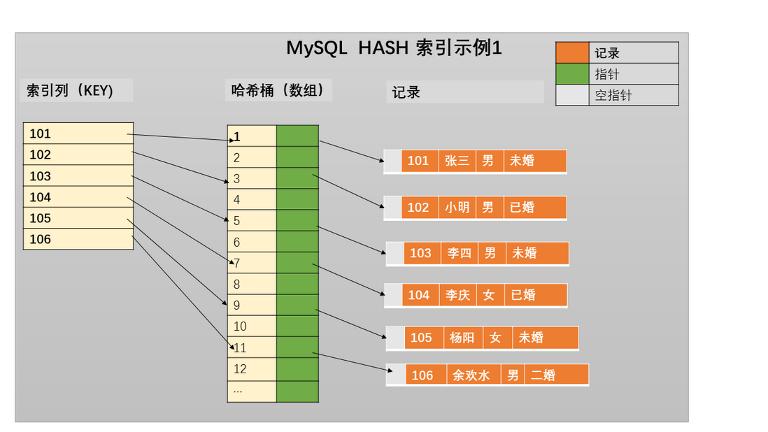
MYSQL——索引概念索引结构
索引 索引是帮助数据库高效获取数据的排好序的数据结构。 有无索引时,查询的区别 主要区别在于查询速度和系统资源的消耗。 查询速度: 在没有索引的情况下,数据库需要对表中的所有记录进行扫描,以找到符合查询条件的记录&#…...
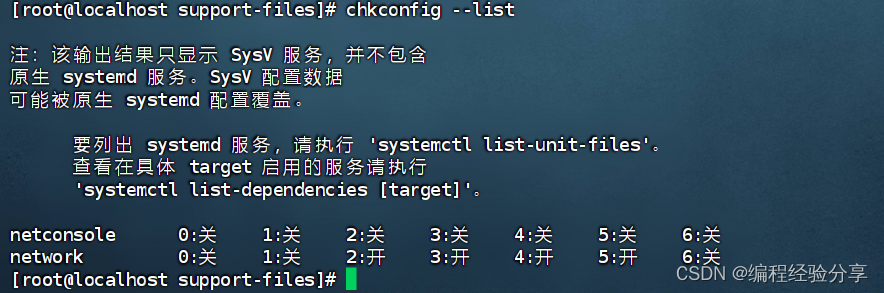
Linux(CentOS7)配置系统服务以及开机自启动
目录 前言 两种方式 /etc/systemd/system/ 进入 /etc/systemd/system/ 文件夹 创建 nginx.service 文件 重新加载 systemd 配置文件 编辑 配置开机自启 /etc/init.d/ 进入 /etc/init.d/ 文件夹 创建 mysql 文件 编写脚本内容 添加/删除系统服务 配置开机自启 …...
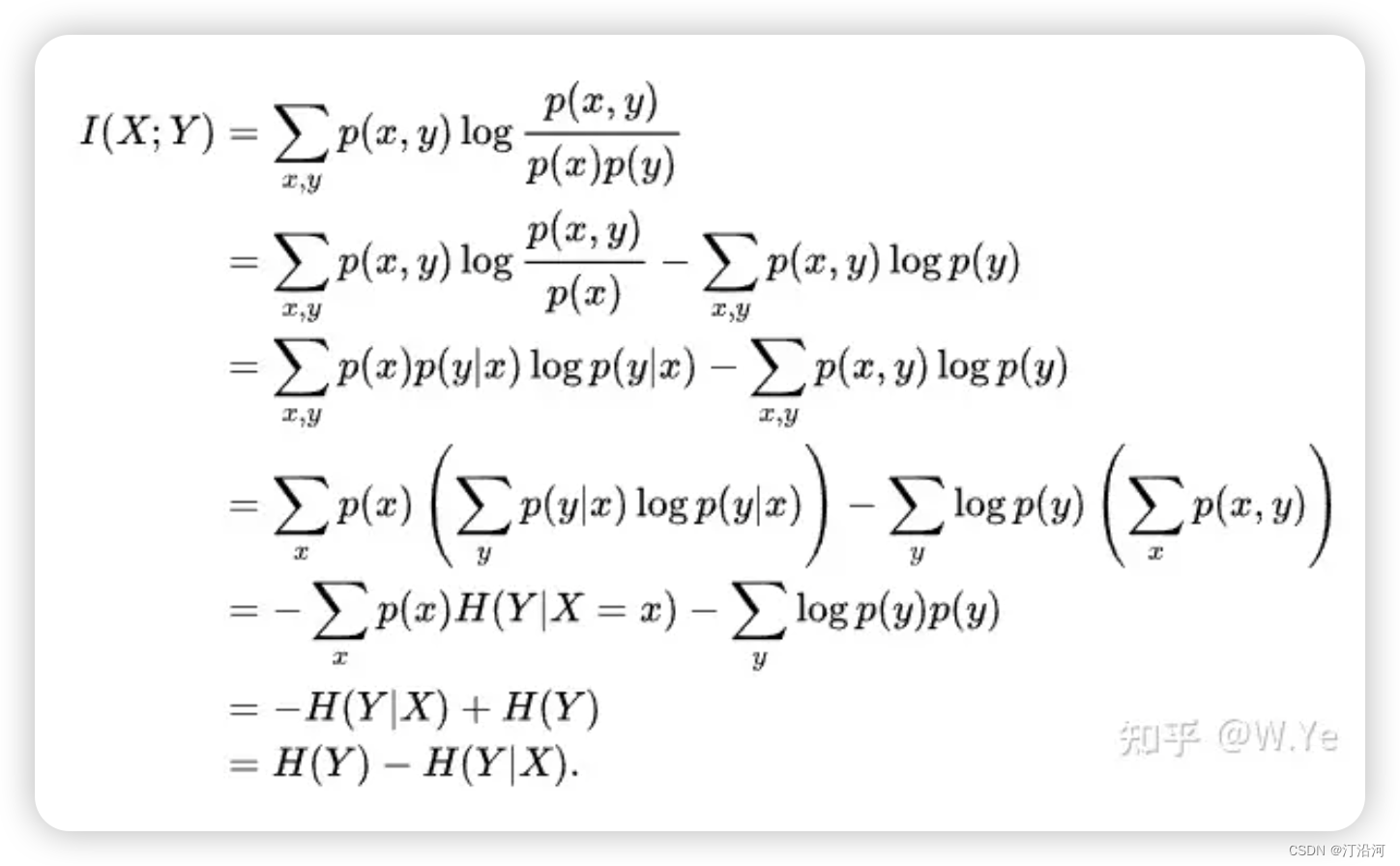
0 决策树基础
目录 1 绪论 2 模型 3 决策树面试总结 1 绪论 决策树算法包括ID3、C4.5以及C5.0等,这些算法容易理解,适用各种数据,在解决各种问题时都有良好表现,尤其是以树模型为核心的各种集成算法,在各个行业和领域都有广泛的…...
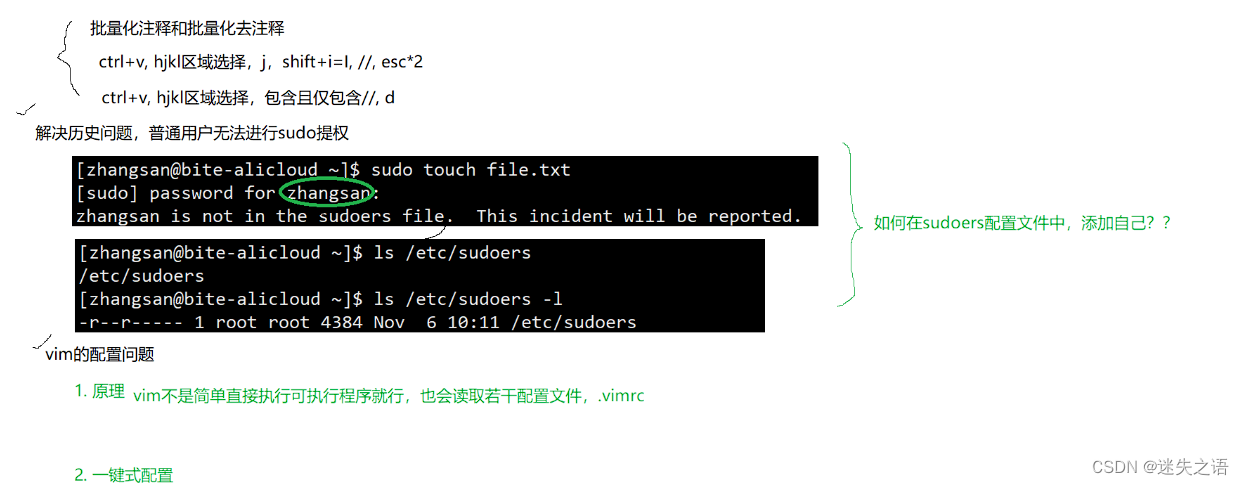
Linux速览(2)——环境基础开发工具篇(其一)
本章我们来介绍一些linux的常用工具 目录 一. Linux 软件包管理器 yum 1.什么是软件包? 2. 查看软件包 3. 如何安装软件 4. 如何卸载软件 5.yum补充 6. 关于 rzsz 二. Linux编辑器-vim使用 1. vim的基本概念 2. vim的基本操作 3. vim正常模式命令集 4. vim末行模式…...

AWS SES发送邮件时常见的错误及解决方法?
AWS SES发送邮件如何做配置?使用AWS SES发信的限制? 在使用AWS SES发送邮件时,可能会遇到一些常见的错误。AokSend将介绍一些常见的AWS SES发送邮件错误及其相应的解决方法,帮助用户更好地利用AWS SES进行邮件发送。 AWS SES发送…...

视频基础学习三——视频帧率、码率与分辨率
文章目录 前言一、介绍1.定义2.三者之间的关系 总结 前言 在之前的文章中详细介绍了一些关于图像的色彩与格式,而视频其实就是由一张张图片进行展示呈现出来的。 我们会经常说一段视频的质量好不好,而什么是视频的质量呢?博主的个人理解就是…...

Spring(详细介绍)
目录 一、简介 1、什么是Spring? 2、Spring框架的核心特性 3、优点 二、IOC容器 介绍 1、获取资源的传统方式 2、控制反转方式获取资源 3、DI 4、IOC容器在Spring中的实现 入门案例 1、创建Maven Module 2、引入依赖 3、创建HelloWorld类 4、在Spring的配…...
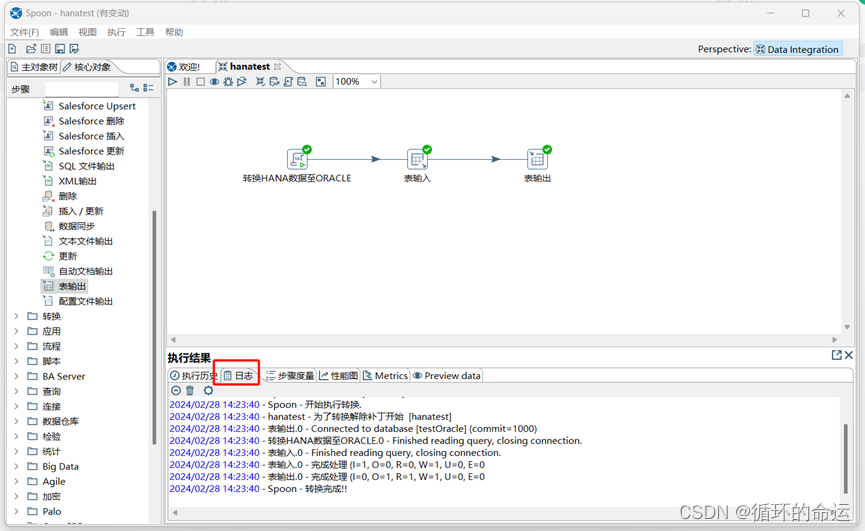
Kettle使用
1.准备工作 KETTLE-5.4.zip HANA环境192.168.xx.xx 用户名:system 密码:****** 端口号:30015 Oracle环境 192.168.xx.xx 用户名 HANA_TEST 密码 ****** 端口号:31001 配置java环境变量 因为本次数据转换测试为将HANA数据转换到Or…...
)
互联网摸鱼日报(2024-04-01)
互联网摸鱼日报(2024-04-01) 36氪新闻 「矽迪半导体」获数千万天使轮融资,提供高效功率半导体方案|硬氪首发 本周双碳大事:国资委即将发布央企ESG指导意见;上海发文推动建立产品碳足迹管理体系;隆基新硅片面世 数字…...

pnpm比npm、yarn好在哪里?
前言 pnpm对比npm/yarn的优点: 更快速的依赖下载更高效的利用磁盘空间更优秀的依赖管理 我们按照包管理工具的发展历史,从 npm2 开始讲起: npm2 使用早期的npm1/2安装依赖,node_modules文件会以递归的形式呈现,严格…...

大前端-postcss安装使用指南
PostCSS 是一款强大的 CSS 处理工具,可以用来自动添加浏览器前缀、代码合并、代码压缩等,提升代码的可读性,并支持使用最新的 CSS 语法。以下是一份简化的 PostCSS 安装使用指南: 一、安装 PostCSS 在你的项目目录中,…...
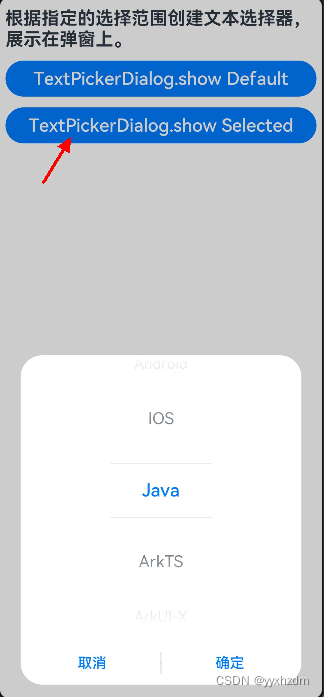
全局UI方法-弹窗三-文本滑动选择器弹窗(TextPickDialog)
1、描述 根据指定的选择范围创建文本选择器,展示在弹窗上。 2、接口 TextPickDialog(options?: TextPickDialogOptions) 3、TextPickDialogOptions 参数名称 参数类型 必填 参数描述 rang string[] | Resource 是 设置文本选择器的选择范围。 selected nu…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
