竞赛常考的知识点大总结(七)图论
最短路
最短路问题(Shortest Path Problem)是图论中的一个经典问题,它要求在给定的图中找到两个顶点之间的最短路径。最短路问题可以是单源最短路问题(从一个顶点到其他所有顶点的最短路径)或所有对最短路问题(任意两个顶点之间的最短路径)。
特点:
1.图论问题:最短路问题是图论中的一个基本问题,通常在加权图中求解。
2.权重:图中的边具有权重,最短路问题的目标是最小化路径的权重总和。
3.多种算法:存在多种算法可以解决最短路问题,如迪杰斯特拉算法(Dijkstra's Algorithm)、贝尔曼-福特算法(Bellman-Ford Algorithm)、Floyd-Warshall算法等。
4.应用广泛:最短路问题在现实世界中有广泛的应用,如网络路由、交通规划、物流调度等。
常见用法:
1.网络路由:在网络设计中,最短路算法用于确定数据包的最佳传输路径。
2.交通规划:在交通规划中,最短路算法用于计算两点之间的最短行驶路径。
3.物流调度:在物流调度中,最短路算法用于优化货物的配送路径。
4.游戏开发:在游戏开发中,最短路算法用于AI寻路和地图探索。
经典C语言例题:
题目: 使用迪杰斯特拉算法解决单源最短路问题。
示例代码:
#include <stdio.h>
#include <limits.h>// 定义图的结构体
typedef struct Graph {int V; // 顶点数量int** adjMatrix; // 邻接矩阵
} Graph;// 创建图的函数
Graph* createGraph(int V) {Graph* graph = (Graph*)malloc(sizeof(Graph));graph->V = V;graph->adjMatrix = (int**)malloc(V * sizeof(int*));for (int i = 0; i < V; i++) {graph->adjMatrix[i] = (int*)malloc(V * sizeof(int));memset(graph->adjMatrix[i], INT_MAX, V * sizeof(int));graph->adjMatrix[i][i] = 0;}return graph;
}// 添加边的函数
void addEdge(Graph* graph, int src, int dest, int weight) {graph->adjMatrix[src][dest] = weight;graph->adjMatrix[dest][src] = weight; // 无向图
}// 迪杰斯特拉算法函数
void dijkstra(Graph* graph, int src) {int* dist = (int*)malloc(graph->V * sizeof(int));int* sptSet = (int*)malloc(graph->V * sizeof(int));for (int i = 0; i < graph->V; i++) {dist[i] = INT_MAX;sptSet[i] = 0;}dist[src] = 0;for (int count = 0; count < graph->V - 1; count++) {int u = -1, min = INT_MAX;for (int v = 0; v < graph->V; v++) {if (sptSet[v] == 0 && dist[v] <= min) {u = v;min = dist[v];}}sptSet[u] = 1;for (int v = 0; v < graph->V; v++) {if (sptSet[v] == 0 && graph->adjMatrix[u][v] && dist[u] != INT_MAX && dist[u] + graph->adjMatrix[u][v] < dist[v]) {dist[v] = dist[u] + graph->adjMatrix[u][v];}}}printf("Vertex\tDistance from Source\n");for (int i = 0; i < graph->V; i++) {printf("%d\t\t%d\n", i, dist[i]);}free(dist);free(sptSet);
}int main() {Graph* graph = createGraph(9);addEdge(graph, 0, 1, 4);addEdge(graph, 0, 7, 8);addEdge(graph, 1, 2, 8);addEdge(graph, 1, 7, 11);addEdge(graph, 2, 3, 7);addEdge(graph, 2, 8, 2);addEdge(graph, 2, 5, 4);addEdge(graph, 3, 4, 9);addEdge(graph, 3, 5, 14);addEdge(graph, 4, 5, 10);addEdge(graph, 5, 6, 2);addEdge(graph, 6, 8, 6);addEdge(graph, 6, 7, 1);addEdge(graph, 7, 8, 7);dijkstra(graph, 0);free(graph->adjMatrix[0]);free(graph->adjMatrix);free(graph);return 0;
}
例题分析:
1.创建图:createGraph函数创建一个图的结构体,包括顶点数量和邻接矩阵。
2.添加边:addEdge函数向图中添加边,并设置边的权重。
3.迪杰斯特拉算法:dijkstra函数实现迪杰斯特拉算法,计算从源点src到其他所有顶点的最短路径。函数使用一个数组dist来存储到每个顶点的最短路径权重,另一个数组sptSet来标记已经找到最短路径的顶点。
4.打印结果:函数最后打印出每个顶点到源点的最短路径权重。
5.主函数:在main函数中,创建了一个图,并添加了一些边。调用dijkstra函数计算从顶点0到其他所有顶点的最短路径,并打印结果。
这个例题展示了如何在C语言中使用迪杰斯特拉算法解决单源最短路问题。通过这个例子,可以更好地理解迪杰斯特拉算法在解决最短路问题中的应用,以及如何使用邻接矩阵来存储图的信息。迪杰斯特拉算法是一种贪心算法,它通过逐步选择最短的未处理路径来找到最短路径,适用于加权图中的单源最短路问题。
树的直径
树的直径(Diameter of a Tree)是指树中任意两点之间的最长路径的长度。在图论中,树是一种特殊的无向图,它没有环,并且任意两个顶点之间有且仅有一条路径。
特点:
1.最长路径:树的直径是树中任意两点之间的最长路径的长度。
2.无环:树是一种无环的图,这意味着树中不存在循环依赖。
3.唯一路径:在树中,任意两个顶点之间有且仅有一条路径。
4.连通性:树中的任意两个顶点都是连通的。
常见用法:
1.网络设计:在计算机网络中,树的直径可以用来衡量网络的效率,最长路径越短,网络的响应时间越短。
2.数据结构:在数据结构中,树的直径可以用来衡量树的深度,有助于优化树的存储和查询效率。
3.算法设计:在算法设计中,树的直径可以用来衡量算法的性能,最长路径越短,算法的效率越高。
经典C语言例题:
题目: 计算树的直径。
示例代码:
#include <stdio.h>
#include <limits.h>// 定义树的结构体
typedef struct Node {int vertex;struct Node* left;struct Node* right;
} Node;// 创建树的节点
Node* newNode(int v) {Node* node = (Node*)malloc(sizeof(Node));node->vertex = v;node->left = NULL;node->right = NULL;return node;
}// 计算树的直径
int treeDiameter(Node* root) {if (root == NULL) {return 0;}// 计算左右子树的高度int leftHeight = treeDiameter(root->left);int rightHeight = treeDiameter(root->right);// 更新直径int diameter = leftHeight + rightHeight;// 返回当前子树的高度return (leftHeight > rightHeight) ? leftHeight + 1 : rightHeight + 1;
}// 主函数
int main() {Node* root = newNode(1);root->left = newNode(2);root->right = newNode(3);root->left->left = newNode(4);root->left->right = newNode(5);root->right->left = newNode(6);root->right->right = newNode(7);printf("Diameter of the tree is: %d\n", treeDiameter(root));return 0;
}
例题分析:
1.创建树的节点:newNode函数创建树的节点,并初始化节点的值。
2.计算树的直径:treeDiameter函数递归地计算树的直径。函数首先计算左右子树的高度,然后更新直径,最后返回当前子树的高度。
3.主函数:在main函数中,创建了一个树的实例,并调用treeDiameter函数计算树的直径,最后打印结果。
这个例题展示了如何在C语言中使用递归方法来计算树的直径。通过这个例子,可以更好地理解树的直径在解决树形结构问题中的应用,以及如何使用递归技术来高效地解决问题。树的直径是树中任意两点之间的最长路径的长度,通过计算左右子树的高度并更新直径,可以得到整个树的直径。
拓扑排序
拓扑排序(Topological Sorting)是图论中的一种算法,用于对有向无环图(DAG)的顶点进行排序,使得对于图中的每一条有向边(u, v),u在排序中都出现在v之前。拓扑排序通常用于解决依赖关系问题,如课程安排、任务调度等。
特点:
1.有向无环图:拓扑排序只适用于有向无环图,即图中不存在环。
2.排序结果:拓扑排序的结果可能不唯一,因为可能存在多个合法的排序。
3.依赖关系:拓扑排序反映了图中顶点之间的依赖关系,即如果存在一条路径从u到v,则u在排序中必须出现在v之前。
4.应用广泛:拓扑排序在编译器设计、软件工程、项目管理等领域都有广泛应用。
常见用法:
1.课程安排:在大学课程安排中,拓扑排序可以用来确定课程的先修关系。
2.任务调度:在项目管理中,拓扑排序可以用来确定任务的执行顺序。
3.依赖解析:在软件构建系统中,拓扑排序可以用来解析模块之间的依赖关系。
经典C语言例题:
题目: 使用拓扑排序解决课程安排问题。
示例代码:
#include <stdio.h>
#include <stdlib.h>// 定义图的结构体
typedef struct Graph {int V; // 顶点数量int* adjMatrix; // 邻接矩阵
} Graph;// 创建图的函数
Graph* createGraph(int V) {Graph* graph = (Graph*)malloc(sizeof(Graph));graph->V = V;graph->adjMatrix = (int*)malloc(V * V * sizeof(int));return graph;
}// 添加边的函数
void addEdge(Graph* graph, int src, int dest) {graph->adjMatrix[src * graph->V + dest] = 1;
}// 拓扑排序函数
void topologicalSort(Graph* graph, int V, int* order) {int* indegree = (int*)calloc(V, sizeof(int));for (int i = 0; i < V; i++) {for (int j = 0; j < V; j++) {if (graph->adjMatrix[i * V + j] == 1) {indegree[j]++;}}}int queue[V];int front = 0, rear = -1;for (int i = 0; i < V; i++) {if (indegree[i] == 0) {queue[++rear] = i;}}int count = 0;while (front <= rear) {int v = queue[front++];order[count++] = v;for (int i = 0; i < V; i++) {if (graph->adjMatrix[v * V + i] == 1 && --indegree[i] == 0) {queue[++rear] = i;}}}if (count != V) {printf("Graph has a cycle\n");free(indegree);free(queue);return;}printf("Topological order: ");for (int i = 0; i < count; i++) {printf("%d ", order[i]);}printf("\n");free(indegree);free(queue);
}int main() {Graph* graph = createGraph(6);addEdge(graph, 5, 2);addEdge(graph, 5, 0);addEdge(graph, 4, 0);addEdge(graph, 4, 1);addEdge(graph, 2, 3);addEdge(graph, 3, 1);int order[6];topologicalSort(graph, 6, order);return 0;
}
例题分析:
1.创建图:createGraph函数创建一个图的结构体,包括顶点数量和邻接矩阵。
2.添加边:addEdge函数向图中添加边。
3.拓扑排序:topologicalSort函数实现拓扑排序算法。函数首先计算每个顶点的入度,然后将入度为0的顶点入队列。接着,从队列中取出顶点,将其加入排序结果,并将其所有出边对应的顶点的入度减1,如果入度变为0,则加入队列。最后,如果排序结果的顶点数量不等于图的顶点数量,则说明图中有环。
4.打印结果:函数最后打印出拓扑排序的结果。
5.主函数:在main函数中,创建了一个图,并添加了一些边。调用topologicalSort函数计算拓扑排序,并打印结果。
这个例题展示了如何在C语言中使用拓扑排序解决课程安排问题。通过这个例子,可以更好地理解拓扑排序在解决依赖关系问题中的应用,以及如何使用邻接矩阵来存储图的信息。拓扑排序是一种有效的算法,可以用来确定有向无环图中顶点的合法排序,从而解决依赖关系问题。
最小生成树
最小生成树(Minimum Spanning Tree,MST)是图论中的一个概念,它是指在一个加权连通图中,选取的边的权重之和最小,并且包括图中的所有顶点的生成树。最小生成树具有以下特点:
特点:
1.连通性:最小生成树包含图中的所有顶点。
2.无环:最小生成树是一棵树,因此它不包含任何环。
3.权重最小:最小生成树的边的权重之和是所有生成树中最小的。
4.唯一性:在权重不相等的图中,最小生成树是唯一的;如果图中存在权重相同的边,则可能存在多个最小生成树。
常见用法:
1.网络设计:在计算机网络中,最小生成树用于设计最经济的网络连接。
2.电路设计:在电路设计中,最小生成树用于寻找连接所有元件的最短路径。
3.城市规划:在城市规划中,最小生成树用于确定城市中各个区域的最短道路连接。
4.图像处理:在图像处理中,最小生成树用于图像分割和特征提取。
经典C语言例题:
题目: 使用普里姆算法(Prim's Algorithm)解决最小生成树问题。
示例代码:
#include <stdio.h>
#include <limits.h>// 定义图的结构体
typedef struct Graph {int V; // 顶点数量int** adjMatrix; // 邻接矩阵
} Graph;// 创建图的函数
Graph* createGraph(int V) {Graph* graph = (Graph*)malloc(sizeof(Graph));graph->V = V;graph->adjMatrix = (int**)malloc(V * sizeof(int*));for (int i = 0; i < V; i++) {graph->adjMatrix[i] = (int*)malloc(V * sizeof(int));memset(graph->adjMatrix[i], INT_MAX, V * sizeof(int));graph->adjMatrix[i][i] = 0;}return graph;
}// 添加边的函数
void addEdge(Graph* graph, int src, int dest, int weight) {graph->adjMatrix[src][dest] = weight;graph->adjMatrix[dest][src] = weight; // 无向图
}// 普里姆算法函数
void primMST(Graph* graph, int start) {int* key = (int*)malloc(graph->V * sizeof(int));int* parent = (int*)malloc(graph->V * sizeof(int));int* inMST = (int*)calloc(graph->V, sizeof(int));for (int i = 0; i < graph->V; i++) {key[i] = INT_MAX;parent[i] = -1;}key[start] = 0;parent[start] = -1;for (int count = 0; count < graph->V - 1; count++) {int u = -1, min = INT_MAX;for (int v = 0; v < graph->V; v++) {if (inMST[v] == 0 && key[v] <= min) {u = v;min = key[v];}}inMST[u] = 1;for (int v = 0; v < graph->V; v++) {if (graph->adjMatrix[u][v] && inMST[v] == 0 && graph->adjMatrix[u][v] < key[v]) {parent[v] = u;key[v] = graph->adjMatrix[u][v];}}}printf("Edge \tWeight\n");for (int i = 1; i < graph->V; i++) {printf("%d - %d \t%d\n", parent[i], i, graph->adjMatrix[i][parent[i]]);}free(key);free(parent);free(inMST);
}int main() {Graph* graph = createGraph(9);addEdge(graph, 0, 1, 4);addEdge(graph, 0, 7, 8);addEdge(graph, 1, 2, 8);addEdge(graph, 1, 7, 11);addEdge(graph, 2, 3, 7);addEdge(graph, 2, 8, 2);addEdge(graph, 2, 5, 4);addEdge(graph, 3, 4, 9);addEdge(graph, 3, 5, 14);addEdge(graph, 4, 5, 10);addEdge(graph, 5, 6, 2);addEdge(graph, 6, 8, 6);addEdge(graph, 6, 7, 1);addEdge(graph, 7, 8, 7);primMST(graph, 0);free(graph->adjMatrix[0]);free(graph->adjMatrix);free(graph);return 0;
}例题分析:
1.创建图:createGraph函数创建一个图的结构体,包括顶点数量和邻接矩阵。
2.添加边:addEdge函数向图中添加边,并设置边的权重。
3.普里姆算法:primMST函数实现普里姆算法,计算从源点start到其他所有顶点的最小生成树。函数使用三个数组key、parent和inMST来存储每个顶点的最小权重、前驱顶点和是否在最小生成树中。
4.打印结果:函数最后打印出最小生成树的边和权重。
5.主函数:在main函数中,创建了一个图,并添加了一些边。调用primMST函数计算从顶点0到其他所有顶点的最小生成树,并打印结果。
这个例题展示了如何在C语言中使用普里姆算法解决最小生成树问题。通过这个例子,可以更好地理解普里姆算法在解决最小生成树问题中的应用,以及如何使用邻接矩阵来存储图的信息。普里姆算法是一种贪心算法,它通过逐步选择最小权重的边来构建最小生成树,适用于加权图中的最小生成树问题。
相关文章:
图论)
竞赛常考的知识点大总结(七)图论
最短路 最短路问题(Shortest Path Problem)是图论中的一个经典问题,它要求在给定的图中找到两个顶点之间的最短路径。最短路问题可以是单源最短路问题(从一个顶点到其他所有顶点的最短路径)或所有对最短路问题&#x…...
NOSQL - Redis的简介、安装、配置和简单操作
目录 一. 知识了解 1. 关系型数据库与非关系型数据库 1.1 关系型数据库 1.2 非关系型数据库 1.3 区别 1.4 非关系型数据库产生背景 1.5 NOSQL 与 SQL的数据记录对比 2. 缓存相关知识 2.1 缓存概念 2.2 系统缓存 2.3 缓存保存位置及分层结构 二 . redis 相关知识 1.…...

书生·浦语大模型开源体系(二)笔记
💗💗💗欢迎来到我的博客,你将找到有关如何使用技术解决问题的文章,也会找到某个技术的学习路线。无论你是何种职业,我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章,也欢…...
docker-compse安装es(包括IK分词器扩展)、kibana、libreoffice
Kibana是一个开源的分析与可视化平台,设计出来用于和Elasticsearch一起使用的。你可以用kibana搜索、查看存放在Elasticsearch中的数据。 Kibana与Elasticsearch的交互方式是各种不同的图表、表格、地图等,直观的展示数据,从而达到高级的数据…...
Electron 读取本地配置 增加缩放功能(ctrl+scroll)
最近,一个之前做的electron桌面应用,需要增加两个功能;第一是读取本地的配置文件,然后记载配置文件中的ip地址;第二就是增加缩放功能; 第一,配置本地文件 首先需要在vue工程根目录中࿰…...
docker中配置交互式的JupyterLab环境的问题
【报错1】 Could not determine jupyter lab build status without nodejs 【解决措施】安装nodejs(利用conda进行安装/从官网下载进行安装) 1、conda安装 conda install -c anaconda nodejs 安装后出现其他报错:Please install nodejs 5 and npm bef…...

SQLAlchemy 来查询并统计 MySQL 中 JSON 字段的一个值
在使用 SQLAlchemy 来查询并统计 MySQL 中 JSON 字段的一个值时,你可以结合 SQLAlchemy 的 func 模块来实现 SQL 函数的调用,比如 JSON_EXTRACT,并使用 group_by 和 count 方法来进行分组统计。下面是如何在 SQLAlchemy 中实现这一点的基本步…...
)
HTTPS ECDHE 握手解析(计算机网络)
使用了 ECDHE,在 TLS 第四次握手前,客户端就已经发送了加密的 HTTP 数据,而对于 RSA 握手过程,必须要完成 TLS 四次握手,才能传输应用数据。 所以,ECDHE 相比 RSA 握手过程省去了一个消息往返的时间&#…...
在git上先新建仓库-把本地文件提交远程
一.在git新建远程项目库 1.选择新建仓库 以下以gitee为例 2.输入仓库名称,点击创建 这个可以选择仓库私有化还公开权限 3.获取仓库clone链接 这里选择https模式就行,就不需要配置对电脑进行sshkey配置了。只是需要每次提交输入账号密码 二、远…...

Redis 过期删除策略
Redis 过期删除策略 Redis 过期删除策略主要包括两种:惰性删除(Lazy Expiration)和定期删除(Periodic Expiration)。这两种策略通常会配合使用,以在内存使用效率、CPU 资源消耗以及过期键清理的及时性之间…...

MySQL 锁合集与事务隔离级别
概览 在数据库管理中,锁是用来控制多个事务对同一数据的并发访问的机制。InnoDB作为MySQL的默认事务型存储引擎,提供了多种类型的锁来保障事务的隔离性并减少冲突,从而维护数据库的完整性和一致性。以下是InnoDB提供的主要锁类型:…...

题解 -- 第六届蓝桥杯大赛软件赛决赛C/C++ 大学 C 组
https://www.lanqiao.cn/paper/ 1 . 分机号 模拟就行 : inline void solve(){int n 0 ;for(int a1;a<9;a){for(int b0;b<9;b){for(int c0;c<9;c){if(a>b && b>c){n ;}}}}cout << n << endl ; } 2 . 五星填数 直接调用全排列的库函数…...

Lua脚本的使用
一、使用lua脚本扣减单个商品的库存 SpringBootTest class LuaTests {AutowiredStringRedisTemplate stringRedisTemplate;Testvoid test3() {for (int i 1; i < 5; i) {stringRedisTemplate.opsForValue().set("product."i,String.valueOf(i));}}Testvoid test…...
hcia datacom课程学习(5):MAC地址与arp协议
1.MAC地址 1.1 含义与作用 (1)含义: mac地址也称物理地址,是网卡设备在数据链路层的地址,全世界每一块网卡的mac地址都是唯一的,出厂时烧录在网卡上不可更改 (2)作用:…...
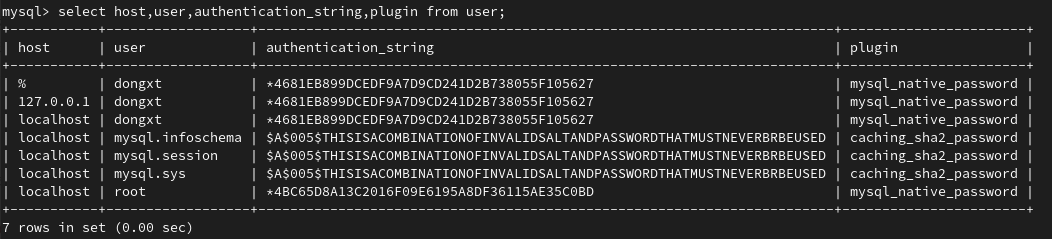
unbuntu mysql8.0新建用户及开启远程连接
MySQL更新到8.0以上版本后,在创建连接远程的用户的时候和之前5.x的版本有了很大的不同,不能使用原来同时创建用户和授权的命令。 以下是记录的MySQL8.0创建用户并授权的命令: 查看用户表: user mysql; select host,user,authen…...

Intel FPGA (1):线性序列机
Intel FPGA (1):线性序列机 前提摘要 个人说明: 限于时间紧迫以及作者水平有限,本文错误、疏漏之处恐不在少数,恳请读者批评指正。意见请留言或者发送邮件至:“Email:noahpanzzzgmail.com”。本博客的工程文件均存放在…...
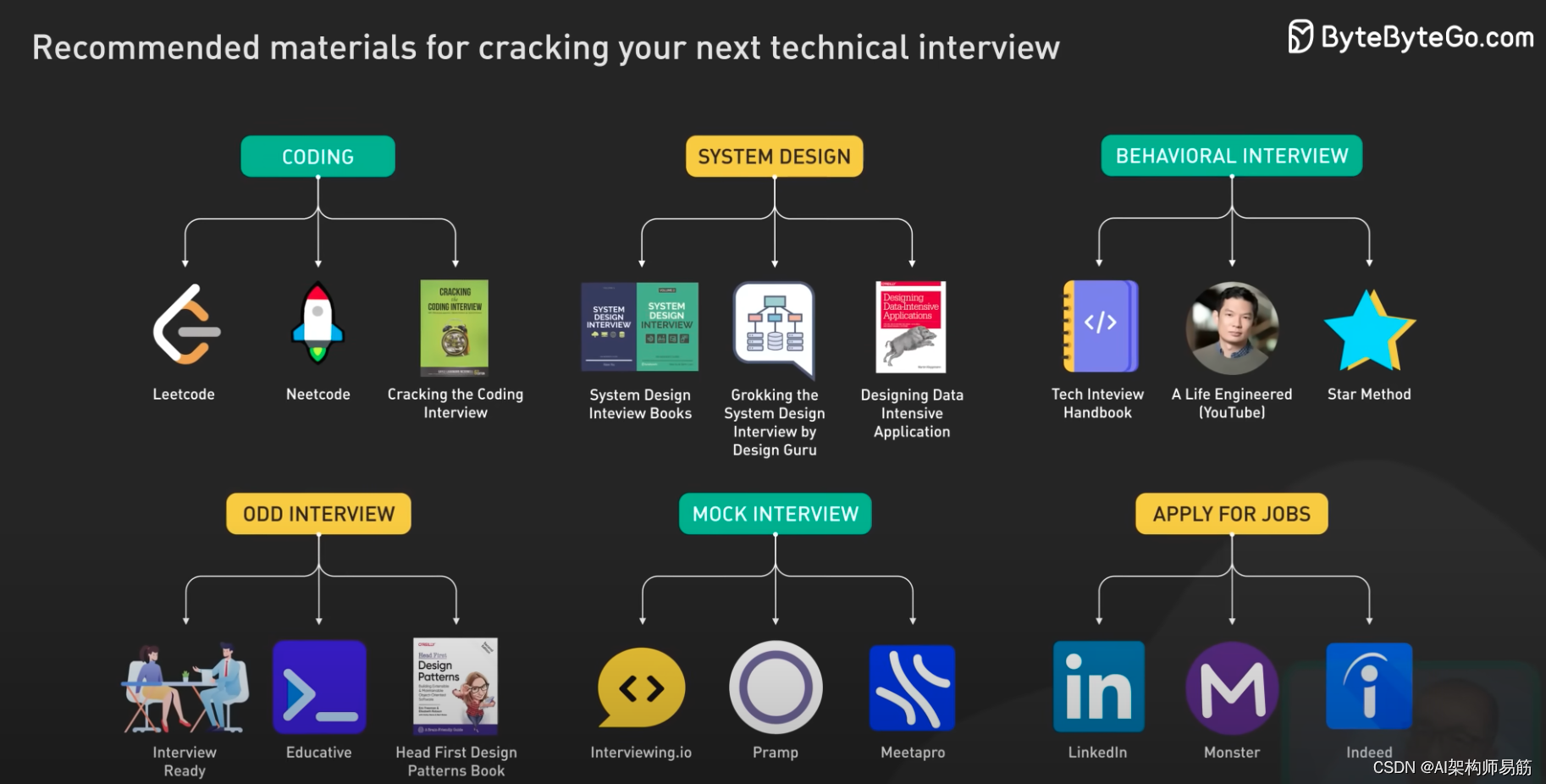
翻译: 硅谷软件工程师面试:准备所需的一切
没有人有时间去做成百上千道LeetCode题目,好消息是你实际上并不需要做那么多题目就能够在FAANG公司找到工作! 我曾经在Grab工作,这是东南亚的一家共享出行公司,但我对工作感到沮丧,想要进入FAANG公司,但我…...
视频推拉流EasyDSS点播平台云端录像播放异常的问题排查与解决
视频推拉流EasyDSS视频直播点播平台可提供一站式的视频转码、点播、直播、视频推拉流、播放H.265视频等服务,搭配RTMP高清摄像头使用,可将无人机设备的实时流推送到平台上,实现无人机视频推流直播、巡检等应用。 有用户反馈,项目现…...

kubuntu23.10安装sdl2及附加库和 sfml2.5.1
2024年3月28号,四,晚上kubuntu23.10下安装了sdl2的如下,没有安装gfx。 sudo apt install libsdl2-dev sudo apt install libsdl2-image-dev sudo apt install libsdl2-ttf-dev sudo apt install libsdl2-mixer-dev sudo apt install libsdl2…...
Centos JDK1.8 下载安装
https://www.oracle.com/java/technologies/javase/javase8u211-later-archive-downloads.html 一 RPM包安装 rpm -ivh jdk-8u391-linux-x64.rpm /etc/profile export JAVA_HOME/usr/java/jdk1.8.0-x64 export PATH$JAVA_HOME/bin:$PATHsource /etc/profile二 tar.gz 包手动…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
