数论与线性代数——整除分块【数论分块】的【运用】【思考】【讲解】【证明(作者自己证的QWQ)】
文章目录
- 整除分块的思考与运用
- 整除分块的时间复杂度证明 & 分块数量
- 整除分块的公式 & 公式证明
- 公式证明
- 代码code↓
整除分块的思考与运用
整除分块是为了解决一个整数求和问题
题目的问题为: ∑ i = 1 n ⌊ n i ⌋ \sum_{i=1}^{n} \left \lfloor \frac{n}{i} \right \rfloor i=1∑n⌊in⌋
求出上述式子的值为多少?
上述问题等同于 c o d e code code↓
int sum=0;
for(int i=1;i<=n;i++) sum+=n/i;//int是整除类型,所以可以直接整除
return sum;
注意事项: ⌊ x ⌋ \left \lfloor x \right \rfloor ⌊x⌋代表不大于 x x x 的最大整数,也可以成为向下取整
我们不难看出,如果我们直接按题意暴力模拟,则时间复杂度为 O ( n ) O(n) O(n),如果 n n n 比较大就会超时(TLE警告QWQ)
而如果我们将 ⌊ n i ⌋ \left \lfloor \frac{n}{i} \right \rfloor ⌊in⌋ ( 1 ≤ i ≤ n 1 \le i \le n 1≤i≤n) 的值输出一下,就会发现其中有许多值是重复的
输出 ⌊ n i ⌋ \left \lfloor \frac{n}{i} \right \rfloor ⌊in⌋值的 c o d e code code↓
for(int i=1;i<=n;i++) cout<<n/i<<endl;
我们可以举例来看一下:
我们令 n = 8 n=8 n=8 ,则有
| i i i 的值 | i i i = 1 1 1 | i i i = 2 2 2 | i i i = 3 3 3 | i i i = 4 4 4 | i i i = 5 5 5 | i i i = 6 6 6 | i i i = 7 7 7 | i i i = 8 8 8 |
|---|---|---|---|---|---|---|---|---|
| ⌊ n i ⌋ \left \lfloor \frac{n}{i} \right \rfloor ⌊in⌋ 的值 | 8 8 8 | 4 4 4 | 2 2 2 | 2 2 2 | 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 |
此时我们可以明显的看出 ⌊ n i ⌋ \left \lfloor \frac{n}{i} \right \rfloor ⌊in⌋ 的值被明显的分成了几个块,每个块中的块值相同
| 分块 | [ 1 , 1 ] [1,1] [1,1] | [ 2 , 2 ] [2,2] [2,2] | [ 3 , 4 ] [3,4] [3,4] | [ 5 , 8 ] [5,8] [5,8] |
|---|---|---|---|---|
| 块值 | 8 8 8 | 4 4 4 | 2 2 2 | 1 1 1 |
整除分块的时间复杂度证明 & 分块数量
总共需要分少于 2 n 2 \sqrt{n} 2n种块,证明如下:
i ≤ n i \leq n i≤n 时, n i \frac{n}{i} in 的值有 { n 1 , n 2 , n 3 . . . n n } \left \{ \frac{n}{1} ,\frac{n}{2},\frac{n}{3} ...\frac{n}{\sqrt{n} }\right \} {1n,2n,3n...nn}, n i ≥ n \frac{n}{i} \ge \sqrt{n} in≥n,共 n \sqrt{n} n 个,此时 ⌊ n i ⌋ \left \lfloor \frac{n}{i} \right \rfloor ⌊in⌋ 有 n \sqrt{n} n 种取值
i ≥ n i \ge n i≥n 时,有 n i ≤ n \frac{n}{i} \le \sqrt{n} in≤n,此时 ⌊ n i ⌋ \left \lfloor \frac{n}{i} \right \rfloor ⌊in⌋ 也有 n \sqrt{n} n 种取值
两者相加,共 2 n 2 \sqrt{n} 2n种,所以整除分块的数量为 O ( n ) O(\sqrt{n}) O(n) 种,所以整除分块的时间复杂度为 O ( n ) O(\sqrt{n}) O(n)
整除分块的公式 & 公式证明
结论: R = n ⌊ n L ⌋ R=\frac{n}{\left \lfloor \frac{n}{L} \right \rfloor} R=⌊Ln⌋n
每个块中的元素个数为: ( R − L + 1 ) (R-L+1) (R−L+1)
每个块中元素的 ⌊ n i ⌋ \left \lfloor \frac{n}{i} \right \rfloor ⌊in⌋ 值为 ⌊ n L ⌋ \left \lfloor \frac{n}{L} \right \rfloor ⌊Ln⌋
每个块中的和为 a n s = ( R − L + 1 ) × ⌊ n L ⌋ ans=(R-L+1) \times \left \lfloor \frac{n}{L} \right \rfloor ans=(R−L+1)×⌊Ln⌋
公式证明
整除分块出现在能被 n n n 完全整除的数之后,到下一个能被 n n n 整除的数之间
令:当前能被 n n n 整除的数为 x x x,下一个能被 n n n 整除的数为 y y y
则有,整除分块的区间为 [ ( x + 1 ) ∼ y ] [(x+1) \sim y] [(x+1)∼y]
令: L = x + 1 L=x+1 L=x+1, R = y R=y R=y, v a l u e value value为分块区间的值,则有,
v a l u e = ⌊ n x + 1 ⌋ = ⌊ n L ⌋ value =\left \lfloor \frac{n}{x+1} \right \rfloor=\left \lfloor \frac{n}{L} \right \rfloor value=⌊x+1n⌋=⌊Ln⌋
因为, y y y 能被 n n n 完全整除(PS:余数为 0 0 0)
所以, ⌊ n y ⌋ = n y \left \lfloor \frac{n}{y} \right \rfloor= \frac{n}{y} ⌊yn⌋=yn,且, n y = v a l u e \frac{n}{y}=value yn=value,则有,
n y = v a l u e \frac{n}{y}=value yn=value y = n v a l u e y= \frac{n}{value} y=valuen
将 v a l u e = ⌊ n x + 1 ⌋ value =\left \lfloor \frac{n}{x+1} \right \rfloor value=⌊x+1n⌋ 代入原式得:
y = n ⌊ n x + 1 ⌋ y= \frac{n}{\left \lfloor \frac{n}{x+1} \right \rfloor} y=⌊x+1n⌋n
我们将 L = x + 1 L=x+1 L=x+1, R = y R=y R=y 代入原式得:
R = n ⌊ n L ⌋ R= \frac{n}{\left \lfloor \frac{n}{L} \right \rfloor} R=⌊Ln⌋n
因为
⌊ n L ⌋ = ⌊ n R ⌋ \left \lfloor \frac{n}{L} \right \rfloor=\left \lfloor \frac{n}{R} \right \rfloor ⌊Ln⌋=⌊Rn⌋
且因为 ⌊ n R ⌋ = n R \left \lfloor \frac{n}{R} \right \rfloor= \frac{n}{R} ⌊Rn⌋=Rn
因为 ( n / R ) (n/R) (n/R) 能被 n n n 完全整除
所以可以保证 n n n 能完全整除 ⌊ n L ⌋ \left \lfloor \frac{n}{L} \right \rfloor ⌊Ln⌋
所以我们可以得证:
⌊ n ⌊ n L ⌋ ⌋ = n ⌊ n L ⌋ {\left \lfloor \frac{n}{{\left \lfloor \frac{n}{L} \right \rfloor}} \right \rfloor}= \frac{n}{\left \lfloor \frac{n}{L} \right \rfloor} ⌊⌊Ln⌋n⌋=⌊Ln⌋n
证明完毕
细节详解:
在 i n t , l o n g l o n g int,long long int,longlong 等整数类型中,可以直接进行整除,所以上面的得证等同于 R = ( n / ( n / L ) ) R=(n/(n/L)) R=(n/(n/L))
代码code↓
#include <bits/stdc++.h>
using namespace std;
long long n,L,R,ans=0;
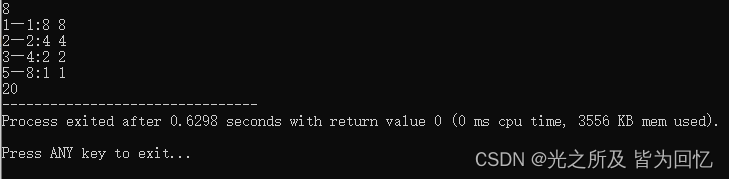
int main(){cin>>n;for(L=1;L<=n;L=R+1){//L=R+1是代表进入下一个块R=n/(n/L);//公式ans+=(R-L+1)*(n/L);//求和cout<<L<<"~"<<R<<":"<<n/R<<" "<<n/L<<endl;//打印分块情况}cout<<ans;//打印和return 0;
}
当 n = 8 n=8 n=8 时的运行结果↓:
相关文章:

数论与线性代数——整除分块【数论分块】的【运用】【思考】【讲解】【证明(作者自己证的QWQ)】
文章目录 整除分块的思考与运用整除分块的时间复杂度证明 & 分块数量整除分块的公式 & 公式证明公式证明 代码code↓ 整除分块的思考与运用 整除分块是为了解决一个整数求和问题 题目的问题为: ∑ i 1 n ⌊ n i ⌋ \sum_{i1}^{n} \left \lfloor \frac{n}{…...
Linux系统下安装jdk与tomcat【linux】
一、yum介绍 linux下的jdk安装以及环境配置,有两种常用方法: 1.使用yum一键安装。 2.手动安装,在Oracle官网下载好需要的jdk版本,上传解压并配置环境。 这里介绍第一种方法,在此之前简单了解下yum。 yum 介绍 yum&…...
matlab实现决策树可视化——信息增益、C4.5、基尼指数
代码:https://download.csdn.net/download/boyas/89074326...

如何使用Python进行网络编程和套接字通信?
如何使用Python进行网络编程和套接字通信? Python作为一种通用编程语言,具有强大的网络编程能力。它提供了丰富的库和工具,使得开发者可以轻松地实现网络编程和套接字通信。下面将详细介绍如何使用Python进行网络编程和套接字通信。 一、网…...
nodeJs 实现视频的转换(超详细教程)
前段时间拿到一个视频是4k的,没法播放,于是通过 node.js 和 ffmpeg 实现了视频的转换。在win10 系统下实现。 所需工具 node 16.19 直接安装 ffmpeg-5.1.1-essentials_build 解压后重名 ffmpeg 放到C盘 然后配置下环境变量 Git-2.42.0.2-64-bit 直接…...

Transformer - model architecture
Transformer - model architecture flyfish Transformer总体架构可分为四个部分: 输⼊部分 输出部分 编码器部分 解码器部分 输入部分 输出部分 输⼊部分包含: 源嵌⼊层和位置编码 ⽬标嵌⼊层和位置编码 输出部分包含: 线性层 softmax处理器 左侧编码器部分和右侧解码器部…...

Zookeeper学习一
初识 Zookeeper Zookeeper 是 Apache Hadoop 项目下的一个子项目,是一个树形目录服务(B树)。 Zookeeper 翻译过来就是 动物园管理员,他是用来管 Hadoop(大象)、Hive(蜜蜂)、Pig(小 猪)的管理员。简称zk …...
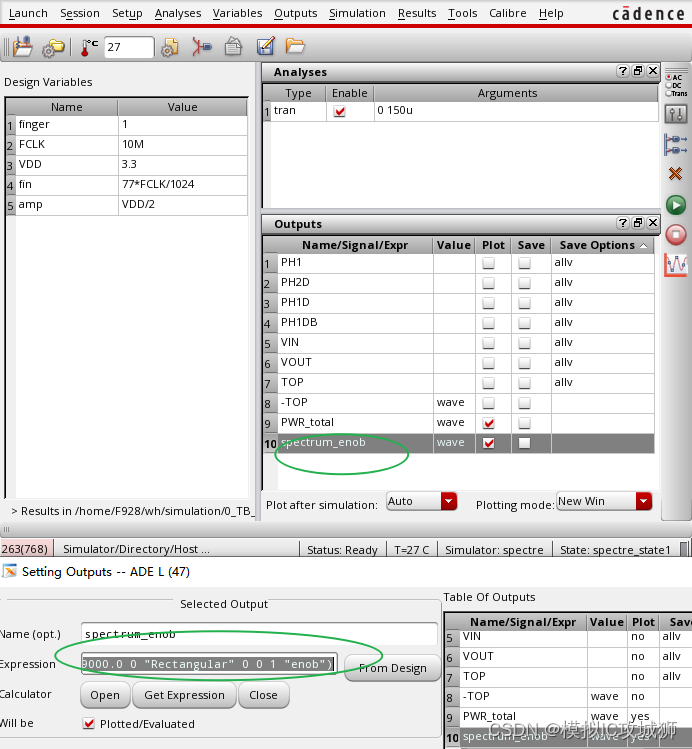
SAR教程系列7——在cadence中用Spectrum工具FFT仿真ADC的ENOB、SNR等动态性能指标
首先在仿真之前,你得有一个ADC。然后是思考如何仿真的问题,如何加激励,如何使用相关工具查看仿真结果。假定你有一个可以仿真的ADC,大致经过下列步骤可以得到ADC的相关动态性能指标。 第一步:在ADC后面接一个理想的DA…...
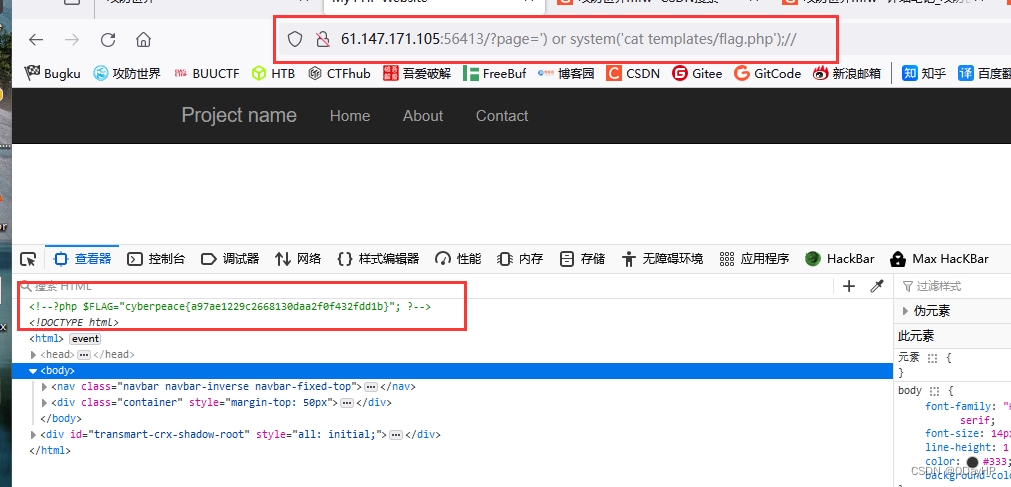
攻防世界:mfw[WriteUP]
根据题目提示考虑是git库泄露 这里在地址栏后加.git也可以验证是git库泄露 使用GitHack工具对git库进行恢复重建 在templates目录下存在flag.php文件,但里面并没有flag 有内容的只有主目录下的index.php index.php源码: <?phpif (isset($_GET[page…...

mysq性能优化-my.cnf配置文件参数调整
MySQL 优化配置文件(my.cnf 或 my.ini)是调整 MySQL 服务器性能的重要手段之一。以下是一些常见的场景,可以通过调整配置文件参数值来优化 MySQL: 1. **提高并发处理能力**: - innodb_buffer_pool_size:增…...

ddres( ) 组站星双差方程和设计矩阵
1 ddres( )参数介绍 rtklib中进行的单频解算 双差观测值,单差的模糊度 单频点双差 DD (double-differenced) phase/code residuals ------------------------------ x 模糊度 P 方差-协方差阵 sat 共识卫星列表 ns 共识卫星数量 y…...

【OpenCV】图像像素的遍历
1 前言 介绍两种遍历像素的方法(非指针、指针)。注意:.at() .ptr()的作用、用法。相关API: Mat对象.ptr() Mat对象.at() 2 代码及内容 #include "iostream" #include "opencv2/opencv.hpp"using namespac…...
构建高可用网络应用:使用Nginx进行负载均衡与健康检查)
(超简单)构建高可用网络应用:使用Nginx进行负载均衡与健康检查
当构建高可用的网络应用时,负载均衡是至关重要的技术之一。Nginx 是一个强大的开源反向代理服务器,提供了丰富的负载均衡功能,包括负载均衡算法和健康检查。在本篇博客中,我们将讨论如何使用 Nginx 进行负载均衡,并结合…...
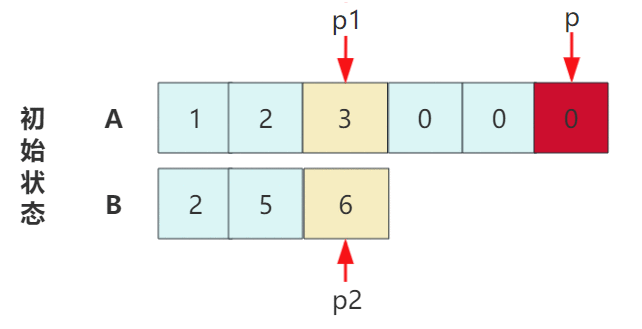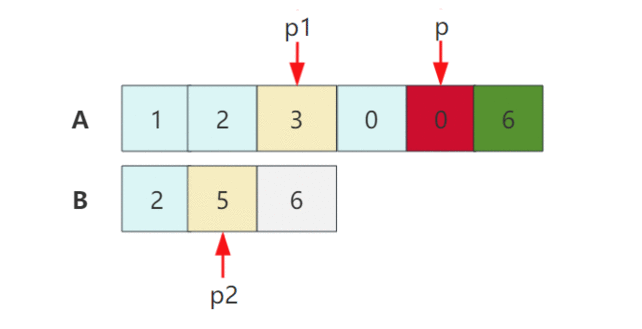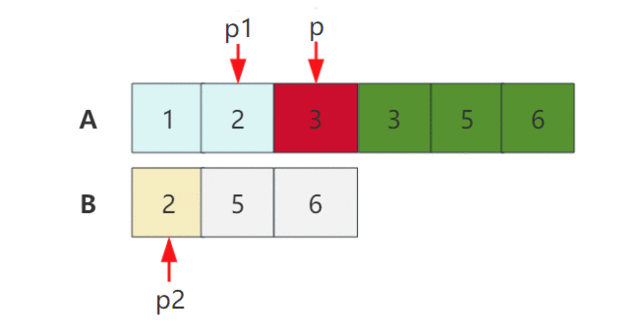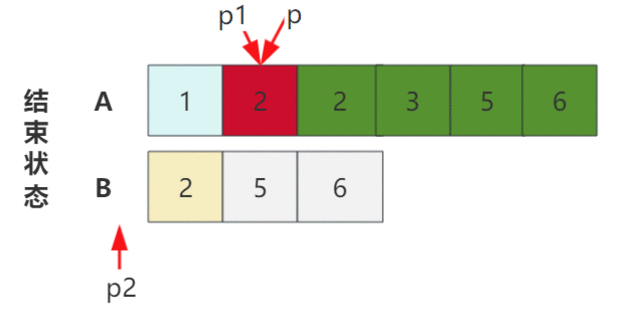
华为OD面试手撕算法-合并排序数组
题目描述 本题是leetcode一道简单题:合并两个有序数组,但是对于时间和空间复杂度面试官明确给出了限制。 // 给定两个排序后的数组 A 和 B,其中 A 的末端有足够的缓冲空间容纳 B。 编写一个方法,将 B 合并入 A 并排序。 // 初始化…...

云智慧发布对象关系型数据库CloudPanguDB,打破传统技术壁垒
近日,云智慧推出关系型数据库CloudPanguDB(中文名称:盘古数据库),旨在通过高兼容性能和创新技术架构,降低企业项目整体运营成本。 无论是处理海量复杂数据,还是构建清晰有序的数据结构关系&…...

6.8物联网RK3399项目开发实录-驱动开发之RTC实时时钟的使用(wulianjishu666)
90款行业常用传感器单片机程序及资料【stm32,stc89c52,arduino适用】 链接:https://pan.baidu.com/s/1M3u8lcznKuXfN8NRoLYtTA?pwdc53f RTC 使用 简介 AIO-3399J 开发板上有 一个集成于 RK808 上的RTC(Real Time Clock),主要功能有时钟,…...

VUE——概述
vue是前端框架,基于MVVM思想。 引入 从官网下载vue文件 <script src"js/vue.js"></script> 定义vue对象 new Vue({el: "#x",//vue接管区域,#表示选择器,x是id名字data: {message: "y"} })案例…...
)
合宙4G模块Air724UG调试过程(短信发送、上传数据到华为云IOT)
合宙Air724UG-4G模块AT指令调试接线演示 一、前言 上海合宙Air724UG模块是一款高性能的4G Cat.1通信模组(全网通模块,支持移动、联通、电信,支持短信和网络通信),为开发者提供了丰富的接口和开发方式。 在本文中,将详述调试与集成该模块的关键步骤: (1)从基础硬件配…...

【项目新功能开发篇】需求分析和开发设计
作者介绍:本人笔名姑苏老陈,从事JAVA开发工作十多年了,带过大学刚毕业的实习生,也带过技术团队。最近有个朋友的表弟,马上要大学毕业了,想从事JAVA开发工作,但不知道从何处入手。于是࿰…...

CentOS 7 下离线安装RabbitMQ教程
CentOS 7 下安装RabbitMQ教程一、做准备(VMWare 虚拟机上的 CentOS 7 镜像 上安装的) (1)准备RabbitMQ的安装包(rabbitmq-server-3.8.5-1.el7.noarch)下载地址mq https://github.com/rabbitmq/rabbitmq-se…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
