深入理解数据结构第二弹——二叉树(2)——堆排序及其时间复杂度
看这篇前请先把我上一篇了解一下:深入理解数据结构第一弹——二叉树(1)——堆-CSDN博客
前言:
相信很多学习数据结构的人,都会遇到一种情况,就是明明最一开始学习就学习了时间复杂度,但是在后期自己写的程序或者是做到哪个需要判断时间复杂度的题时,仍然判断不出来时间复杂度是多少,今天,我们结合我们上期学习的堆,给大家深入剖析一下时间复杂度这个概念,同时更深入的理解堆的概念,方便我们后期应用堆进行排序等。
目录
一、堆排序
1、堆排序的大体思路
2、堆排序的实例讲解
二、堆排序的时间复杂度
向下排序的时间复杂度
向上排序的时间复杂度
堆排序整体的时间复杂度
总结
一、堆排序
1、堆排序的大体思路
在上一篇我们已经讲过了堆是什么东西,我们已经知道堆有大堆和小堆两种形式,堆排序的想法正是借助它的这个特点诞生的,例如:
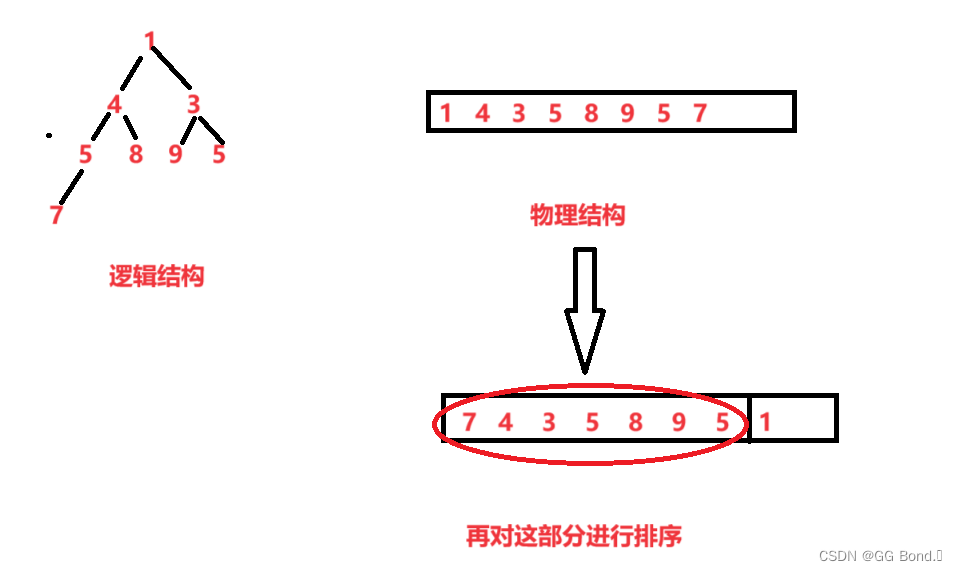
数组 { 7,8 ,3 ,5 ,1 ,9 ,5 ,4}在堆中分布为:

如图展示的是小堆,首先我们先强调一点,降序是需要小堆来解决,升序是需要大堆来解决
比如说图上这个数组,我们要求它的降序序列时,因为堆顶元素一定是堆中最小的,所以我们就可以把堆顶元素与堆尾元素进行交换,然后把堆尾元素刨除在外再进行降序排列
2、堆排序的实例讲解
堆排序与堆相比并没有什么新东西,把我前面那章看明白,这里直接把代码呈上
(除了test.c)其他的是直接从上一章搬过来的
Seqlist.h
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int sz;int capacity;
}HP;//初始化
void HeapInit(HP* php);
//销毁
void HeapDestory(HP* php);
//插入
void HeapPush(HP* php, HPDataType x);
//删除
void HeapPop(HP* php);
//找堆顶元素
HPDataType HeapTop(HP* php);
//判断是否为空
bool HeapEmpty(HP* php);
//算个数
int HeapSize(HP* php);test.c
//堆排序
void HeapSort(int* a, int n)
{//建堆——向下调整建堆O(N-log(n))for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);//再调整,选出次小数AdjustDown(a, end, 0);end--;}
}
int main()
{int a[] = { 7,8,3,5,1,9,5,4 };HeapSort(a, sizeof(a) / sizeof(int));return 0;
}Seqlist.c
//堆
//初始化
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->capacity = 0;php->sz = 0;
}
//销毁
void HeapDestory(HP* php)
{free(php->a);free(php);
}
//交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//删除//向上调整(小堆)
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
//向下调整
void AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child<n){if (child+1<n&&a[child + 1] < a[child]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}//插入
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->sz == php->capacity){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);php->a = tmp;php->capacity = newcapacity;}php->a[php->sz] = x;php->sz++;//向上调整AdjustUp(php->a, php->sz - 1);
}
//删除
void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->sz - 1]);php->sz--;//向下调整AdjustDown(php->a, php->sz,0);
}
//判断是否为空
bool HeapEmpty(HP* php)
{assert(php);return php->sz == 0;
}
//找堆顶元素
HPDataType HeapTop(HP* php)
{assert(php);assert(!HeapEmpty(php));return php->a[0];
}
//算个数
int HeapSize(HP* php)
{assert(php);return php->sz;
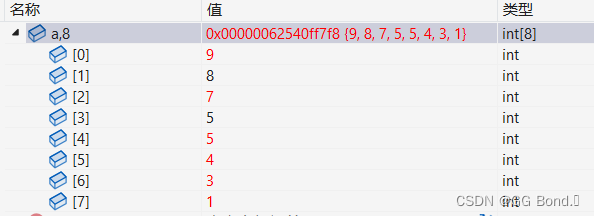
}实现上述代码,我们就可以实现堆排序了
二、堆排序的时间复杂度
我们都知道在实现堆时有向上排序和向下排序两种,细心的人可能已经注意到,我在实现上面那个堆排序用例时,用的是向下排序,原因就是向下排序的时间复杂度更低,接下来,我们就来分析一下这两种排序各自的时间复杂度
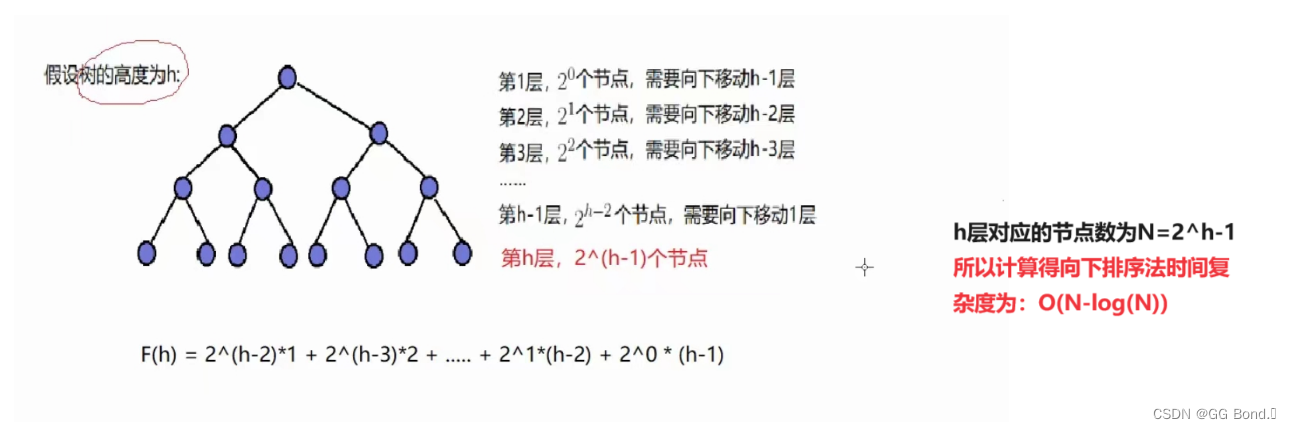
向下排序的时间复杂度
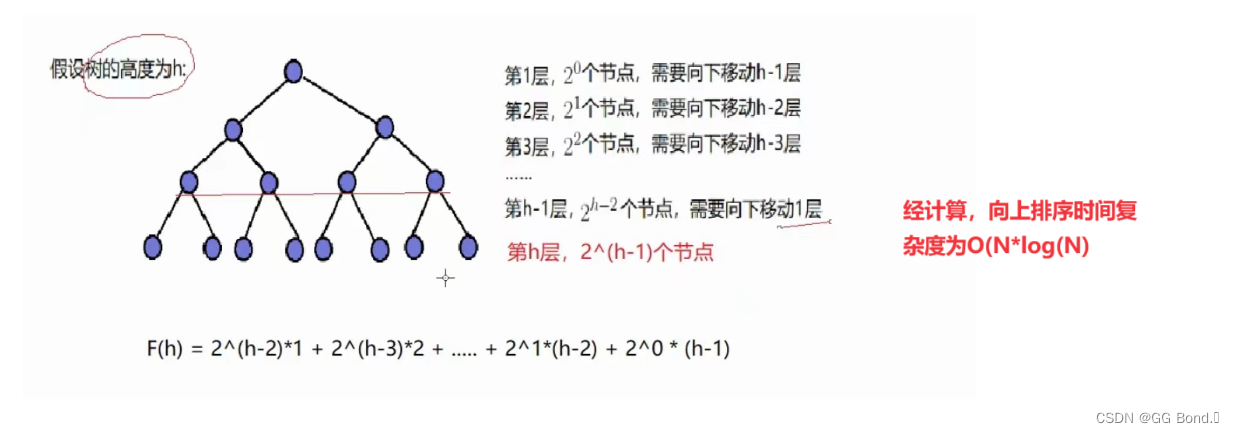
向上排序的时间复杂度
堆排序整体的时间复杂度

计算堆排序整体的时间复杂度就是计算上面这两步的时间复杂度
第一步:
因为这一步实际上就是多次向下调整建堆,所以这一步时间复杂度就是向下调整法时间复杂度的倍数,那根据渐进表示法就可以表示为O(N-log(N)),因为当N很大时,log(N)比N小很多,所以可以忽略表示为O(N)
第二步:
第二步外循环需要N次,内循环看似每次都是一个完整的向下排序法,但其实随着循环次数的增加,里面向下排序的时间复杂度在不断减小,因为堆尾排过去的数字实际上就不用再参与堆排序的,所以这一步时间复杂度实际上是O(N*log)
因此,堆排序的时间复杂度为O(N+N*log(N))
总结
堆排序及其时间复杂度的讲解就到此为止了,如果有不理解的地方欢迎在评论区中指出或者与我私信交流,欢迎各位大佬来访!!!
创作不易,还请各位大佬点赞支持!!!
相关文章:

深入理解数据结构第二弹——二叉树(2)——堆排序及其时间复杂度
看这篇前请先把我上一篇了解一下:深入理解数据结构第一弹——二叉树(1)——堆-CSDN博客 前言: 相信很多学习数据结构的人,都会遇到一种情况,就是明明最一开始学习就学习了时间复杂度,但是在后期…...

视频汇聚/安防监控/EasyCVR平台播放器EasyPlayer更新:新增【性能面板】
视频汇聚/安防监控/视频存储平台EasyCVR基于云边端架构,可以在复杂的网络环境中快速、灵活部署,平台视频能力丰富,可以提供实时远程视频监控、视频录像、录像回放与存储、告警、语音对讲、云台控制、平台级联、磁盘阵列存储、视频集中存储、云…...

【教程】Flutter 应用混淆
在移动应用开发中,保护应用代码安全至关重要。Flutter 提供了简单易用的混淆工具,帮助开发者在构建 release 版本应用时有效保护代码。本文将介绍如何在 Flutter 应用中使用混淆,并提供了相关的操作步骤和注意事项。 📝 摘要 本…...

STM32中C编程引入C++程序
C具备类的创建思想很实用于实际场景多相似性的框架搭建;同种类型或相似类型的C的优势明显因此进行相互嵌套使用 需要在C中使用C类的话,你可以通过C的“extern "C"”语法来实现。这允许你在C代码中使用C的链接方式,而在C代码中使用…...

MySQL DBA 需要了解一下 InnoDB Online DDL 算法更新
在 MySQL 8.0.12 中,我们引入了一种新的 DDL 算法,该算法在更改表的定义时不会阻塞表。第一个即时操作是在表格末尾添加一列,这是来自腾讯游戏的贡献。 然后在 MySQL 8.0.29 中,我们添加了在表中任意位置添加(或删除&…...

多态--下
文章目录 概念多态如何实现的指向谁调谁?例子分析 含有虚函数类的大小是多少?虚函数地址虚表地址多继承的子类的大小怎么计算?练习题虚函数和虚继承 概念 优先使用组合、而不是继承; 继承会破坏父类的封装、因为子类也可以调用到父类的函数;…...
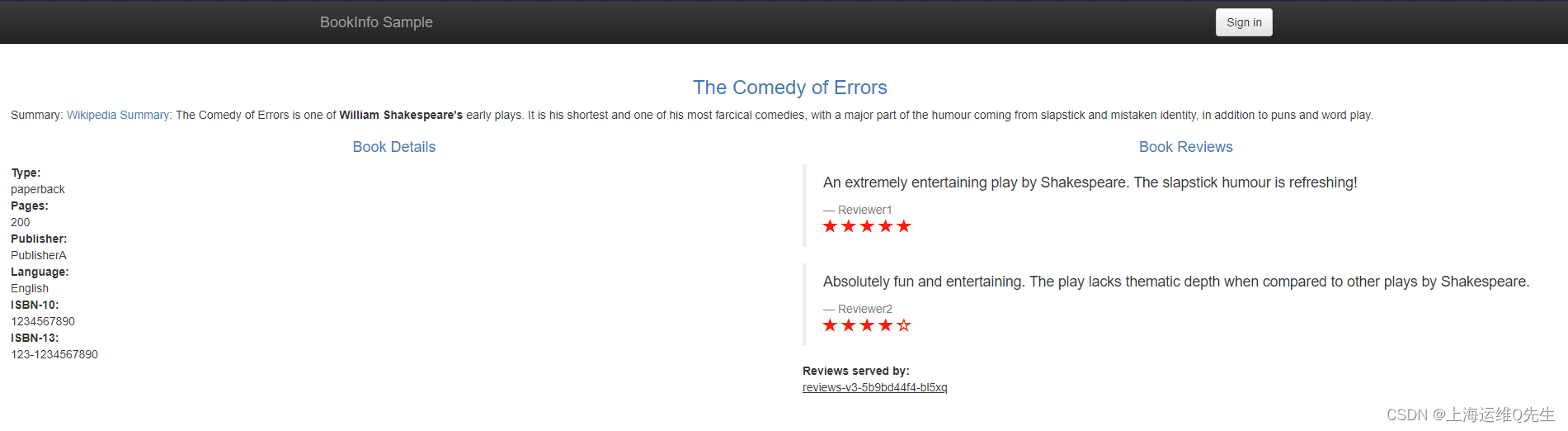
备考ICA----Istio实验16---HTTP流量授权
备考ICA----Istio实验16—HTTP流量授权 1. 环境准备 kubectl apply -f istio/samples/bookinfo/platform/kube/bookinfo.yaml kubectl apply -f istio/samples/bookinfo/networking/bookinfo-gateway.yaml访问测试 curl -I http://192.168.126.220/productpage2. 开启mtls …...
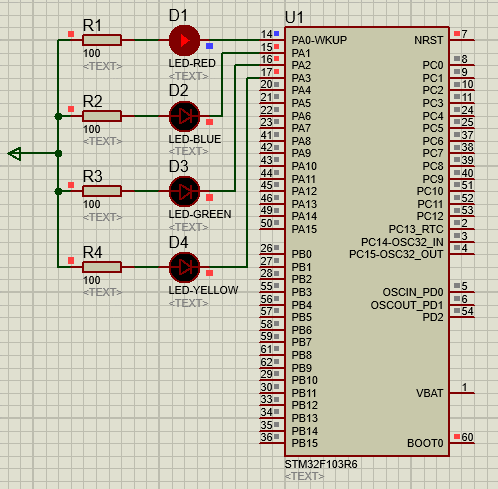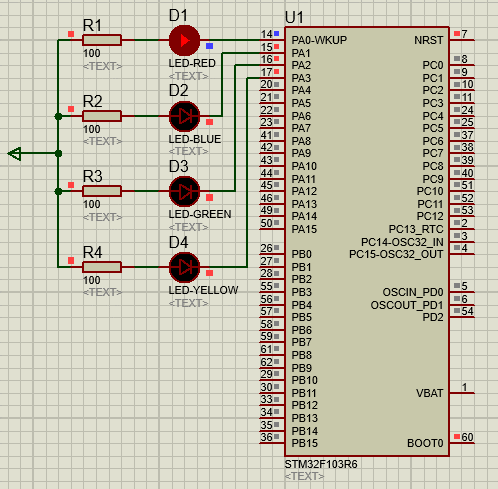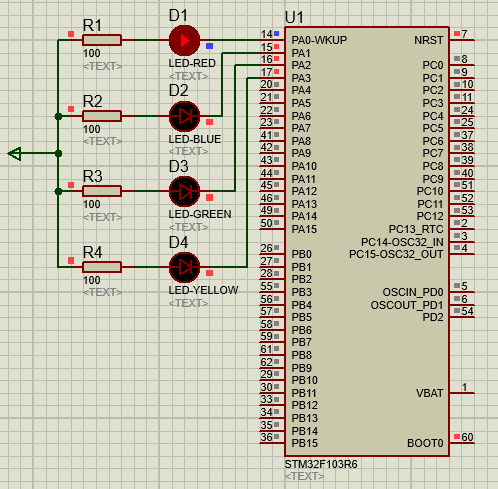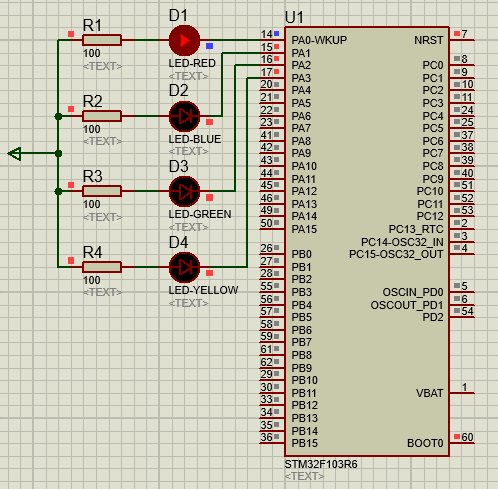
STM32-02基于HAL库(CubeMX+MDK+Proteus)GPIO输出案例(LED流水灯)
文章目录 一、功能需求分析二、Proteus绘制电路原理图三、STMCubeMX 配置引脚及模式,生成代码四、MDK打开生成项目,编写HAL库的GPIO输出代码五、运行仿真程序,调试代码 一、功能需求分析 在完成开发环境搭建之后,开始使用STM32GP…...
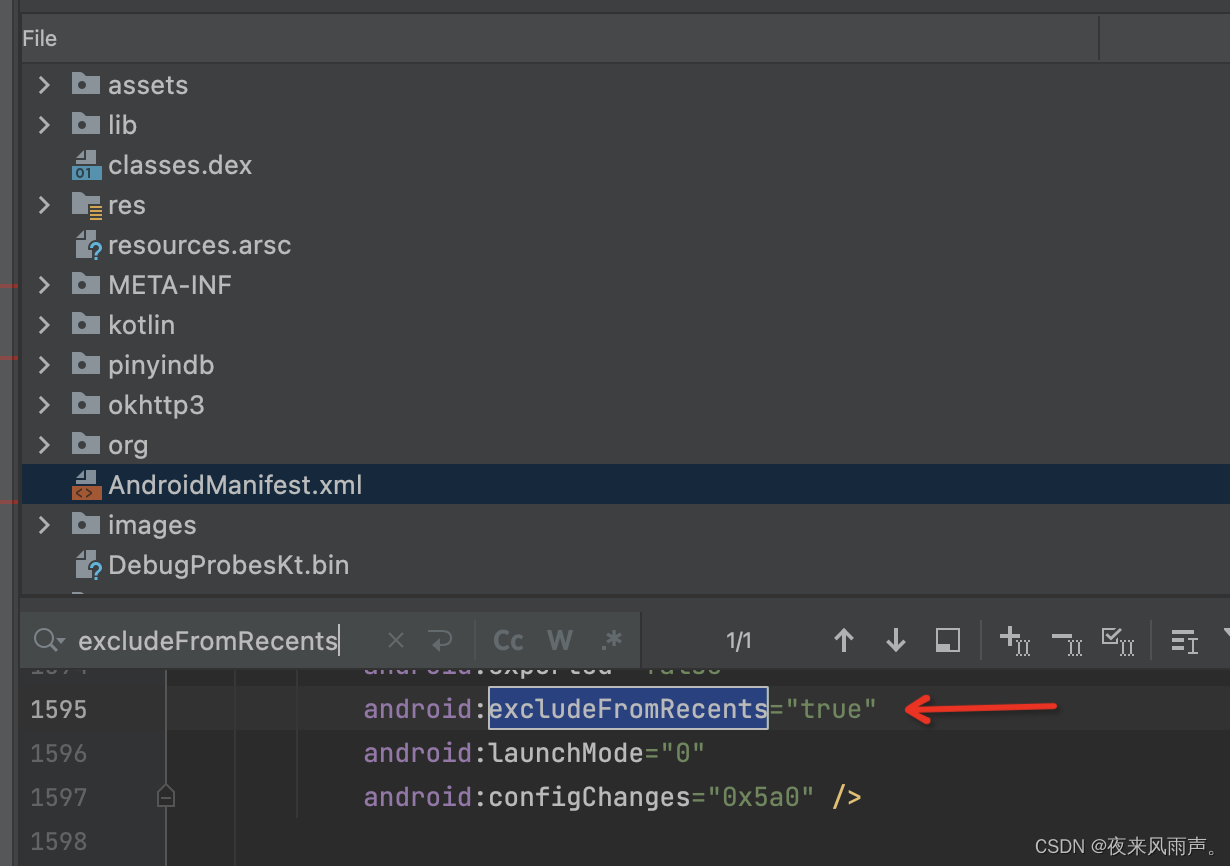
华为审核被拒提示: 您的应用存在(最近任务列表隐藏风险活动)的行为,不符合华为应用市场审核标准
应用审核意见: 您的应用存在(最近任务列表隐藏风险活动)的行为,不符合华为应用市场审核标准。 修改建议:请参考测试结果进行修改。 请参考《审核指南》第2.19相关审核要求:https://developer.huawei.com/c…...
数论与线性代数——整除分块【数论分块】的【运用】【思考】【讲解】【证明(作者自己证的QWQ)】
文章目录 整除分块的思考与运用整除分块的时间复杂度证明 & 分块数量整除分块的公式 & 公式证明公式证明 代码code↓ 整除分块的思考与运用 整除分块是为了解决一个整数求和问题 题目的问题为: ∑ i 1 n ⌊ n i ⌋ \sum_{i1}^{n} \left \lfloor \frac{n}{…...
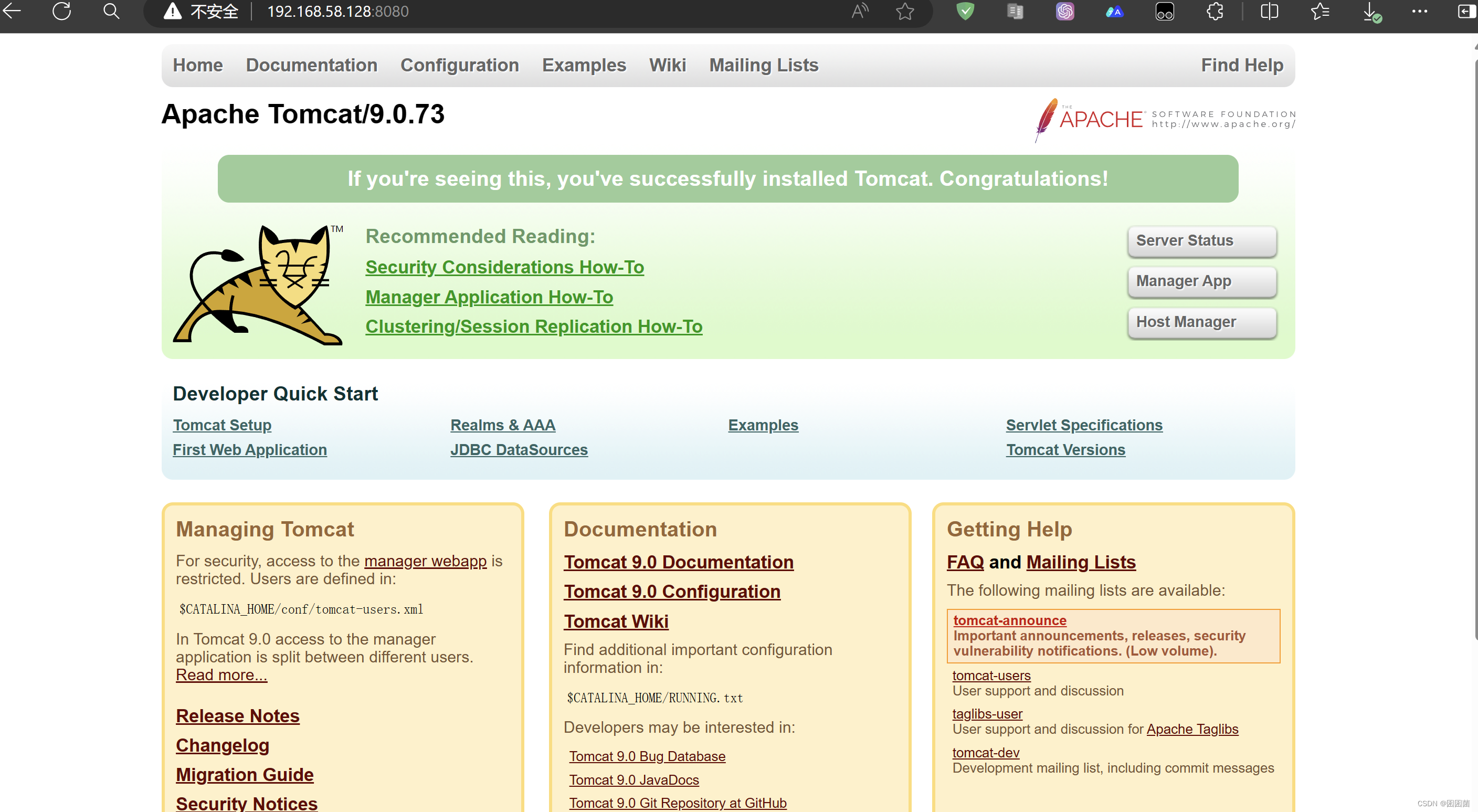
Linux系统下安装jdk与tomcat【linux】
一、yum介绍 linux下的jdk安装以及环境配置,有两种常用方法: 1.使用yum一键安装。 2.手动安装,在Oracle官网下载好需要的jdk版本,上传解压并配置环境。 这里介绍第一种方法,在此之前简单了解下yum。 yum 介绍 yum&…...
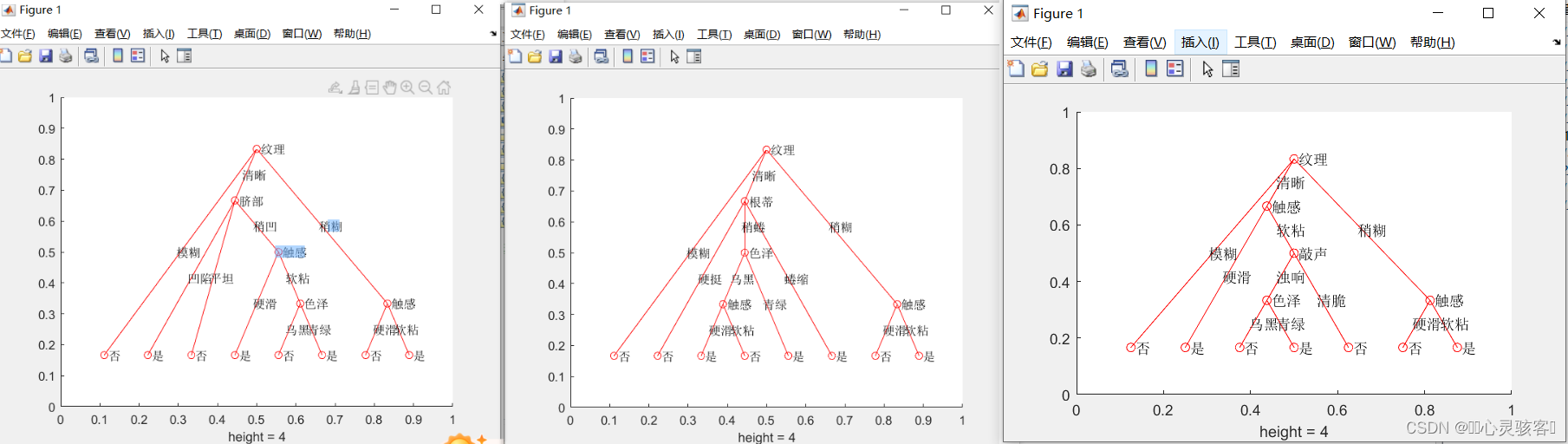
matlab实现决策树可视化——信息增益、C4.5、基尼指数
代码:https://download.csdn.net/download/boyas/89074326...

如何使用Python进行网络编程和套接字通信?
如何使用Python进行网络编程和套接字通信? Python作为一种通用编程语言,具有强大的网络编程能力。它提供了丰富的库和工具,使得开发者可以轻松地实现网络编程和套接字通信。下面将详细介绍如何使用Python进行网络编程和套接字通信。 一、网…...
nodeJs 实现视频的转换(超详细教程)
前段时间拿到一个视频是4k的,没法播放,于是通过 node.js 和 ffmpeg 实现了视频的转换。在win10 系统下实现。 所需工具 node 16.19 直接安装 ffmpeg-5.1.1-essentials_build 解压后重名 ffmpeg 放到C盘 然后配置下环境变量 Git-2.42.0.2-64-bit 直接…...

Transformer - model architecture
Transformer - model architecture flyfish Transformer总体架构可分为四个部分: 输⼊部分 输出部分 编码器部分 解码器部分 输入部分 输出部分 输⼊部分包含: 源嵌⼊层和位置编码 ⽬标嵌⼊层和位置编码 输出部分包含: 线性层 softmax处理器 左侧编码器部分和右侧解码器部…...

Zookeeper学习一
初识 Zookeeper Zookeeper 是 Apache Hadoop 项目下的一个子项目,是一个树形目录服务(B树)。 Zookeeper 翻译过来就是 动物园管理员,他是用来管 Hadoop(大象)、Hive(蜜蜂)、Pig(小 猪)的管理员。简称zk …...
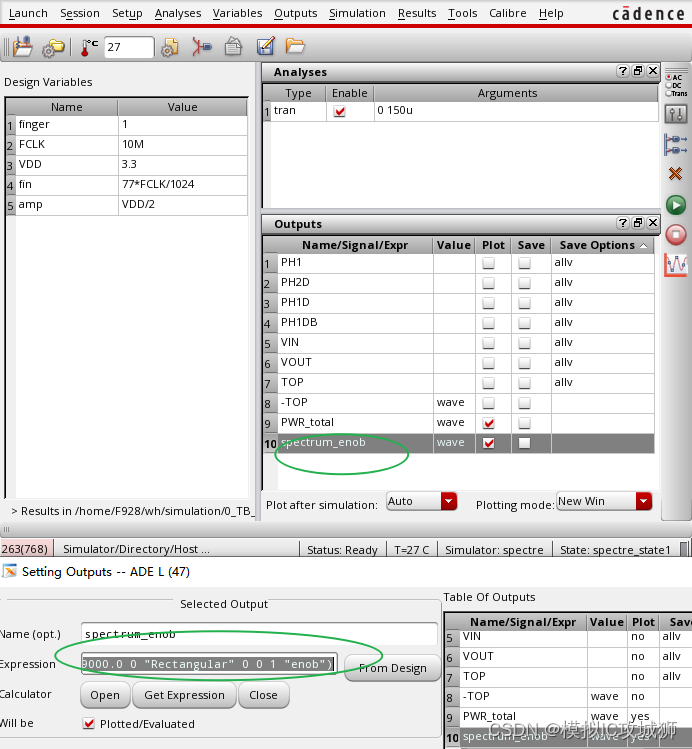
SAR教程系列7——在cadence中用Spectrum工具FFT仿真ADC的ENOB、SNR等动态性能指标
首先在仿真之前,你得有一个ADC。然后是思考如何仿真的问题,如何加激励,如何使用相关工具查看仿真结果。假定你有一个可以仿真的ADC,大致经过下列步骤可以得到ADC的相关动态性能指标。 第一步:在ADC后面接一个理想的DA…...
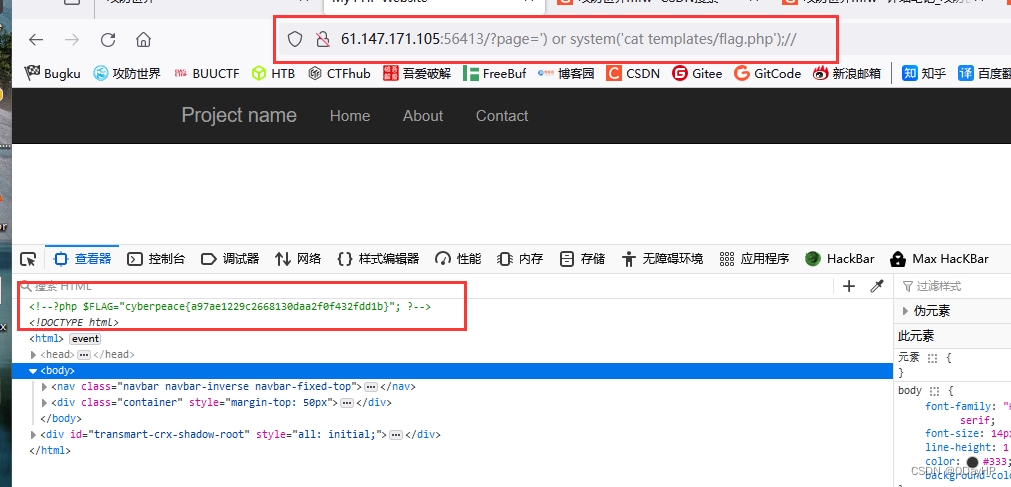
攻防世界:mfw[WriteUP]
根据题目提示考虑是git库泄露 这里在地址栏后加.git也可以验证是git库泄露 使用GitHack工具对git库进行恢复重建 在templates目录下存在flag.php文件,但里面并没有flag 有内容的只有主目录下的index.php index.php源码: <?phpif (isset($_GET[page…...

mysq性能优化-my.cnf配置文件参数调整
MySQL 优化配置文件(my.cnf 或 my.ini)是调整 MySQL 服务器性能的重要手段之一。以下是一些常见的场景,可以通过调整配置文件参数值来优化 MySQL: 1. **提高并发处理能力**: - innodb_buffer_pool_size:增…...

ddres( ) 组站星双差方程和设计矩阵
1 ddres( )参数介绍 rtklib中进行的单频解算 双差观测值,单差的模糊度 单频点双差 DD (double-differenced) phase/code residuals ------------------------------ x 模糊度 P 方差-协方差阵 sat 共识卫星列表 ns 共识卫星数量 y…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

阿里云Ubuntu 22.04 64位搭建Flask流程(亲测)
cd /home 进入home盘 安装虚拟环境: 1、安装virtualenv pip install virtualenv 2.创建新的虚拟环境: virtualenv myenv 3、激活虚拟环境(激活环境可以在当前环境下安装包) source myenv/bin/activate 此时,终端…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...
