图神经网络实战(7)——图卷积网络(Graph Convolutional Network, GCN)详解与实现
图神经网络实战(7)——图卷积网络详解与实现
- 0. 前言
- 1. 图卷积层
- 2. 比较 GCN 和 GNN
- 2.1 数据集分析
- 2.2 实现 GCN 架构
- 小结
- 系列链接
0. 前言
图卷积网络 (Graph Convolutional Network, GCN) 架构由 Kipf 和 Welling 于 2017 年提出,其理念是创建一种适用于图的高效卷积神经网络 (Convolutional Neural Networks, CNN)。更准确地说,它是图信号处理中图卷积操作的近似,由于其易用性,GCN 已成为最受欢迎的图神经网络 (Graph Neural Networks, GNN) 之一,是处理图数据时创建基线模型的首选架构。
在本节中,我们将讨论 Vanilla GNN 架构的局限性,这有助于我们理解 GCN 的核心思想。并详细介绍 GCN 的工作原理,解释为什么 GCN 比 Vanilla GNN 性能更好,通过使用 PyTorch Geometric 在 Cora 和 Facebook Page-Page 数据集上实现 GCN 来验证其性能。
1. 图卷积层
与表格或图像数据不同,图数据中节点的邻居数量并不总是相同。例如,在下图中,节点 1 有 3 个邻居,而节点 2 只有 1 个:

但是,观察图神经网络 (Graph Neural Networks, GNN) 层就会发现,邻居数量的差异并不会导致计算的复杂化。GNN 层由一个简单的求和公式组成,没有任何归一化系数,计算节点 i i i 的嵌入方法如下:
h i = ∑ j ∈ N i x j W T h_i=\sum_{j\in \mathcal N_i}x_jW^T hi=j∈Ni∑xjWT
假设节点 1 有 1,000 个邻居,而节点 2 只有 1 个邻居,那么 h 1 h_1 h1 嵌入的值将远远大于 h 2 h_2 h2 嵌入的值。这样便会出现一个问题,当我们要对这些嵌入进行比较时,如果它们的值相差过大,如何进行有意义的比较?
一个简单的解决方案是将嵌入除以邻居数量,用 deg ( A ) \deg(A) deg(A) 表示节点的度,因此 GNN 层公式可以更新为:
h i = 1 deg ( i ) ∑ j ∈ N i x j W T h_i=\frac 1{\deg(i)}\sum_{j\in \mathcal N_i}x_jW^T hi=deg(i)1j∈Ni∑xjWT
那么如何将其转化为矩阵乘法呢?首先回顾普通 GNN 层的计算公式:
H = A ~ T X W T H=\tilde A^TXW^T H=A~TXWT
其中, A ~ = A + I \tilde A=A+I A~=A+I。公式中缺少的是一个能为我们提供归一化系数 1 deg ( A ) \frac 1 {\deg(A)} deg(A)1 的矩阵,可以利用度矩阵 D D D 来计算每个节点的邻居数量。上示图像中的图的度矩阵如下:
D = [ 3 0 0 0 0 1 0 0 0 0 2 0 0 0 0 2 ] D=\left[\begin{array}{c} 3 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 2 & 0\\ 0 & 0 & 0 & 2\\ \end{array}\right] D= 3000010000200002
使用 NumPy 表示以上矩阵:
import numpy as npD = np.array([[3, 0, 0, 0],[0, 1, 0, 0],[0, 0, 2, 0],[0, 0, 0, 2]
])
根据定义, D D D 给出了每个节点的度 deg ( i ) \deg(i) deg(i) 。因此,根据度矩阵的逆矩阵 D − 1 D^{-1} D−1 可以直接得到归一化系数 1 deg ( A ) \frac 1 {\deg(A)} deg(A)1:
可以使用 numpy.linalg.inv() 函数计算矩阵的逆:
print(np.linalg.inv(D))
'''输出如下
[[0.33333333 0. 0. 0. ][0. 1. 0. 0. ][0. 0. 0.5 0. ][0. 0. 0. 0.5 ]]
'''
为了更加精确,在图中添加了自循环,用 A ~ = A + I \tilde A=A+I A~=A+I 表示。同样,我们也需要在度矩阵中加入自循环,即 D ~ = D + I \tilde D= D+I D~=D+I ,因此最终所需的矩阵为 D ~ − 1 = ( D + I ) − 1 \tilde D^{-1} = (D+I)^{-1} D~−1=(D+I)−1:
在 NumPy 中,可以使用函数 numpy.identity(n) 快速创建指定维度 n 的单位矩阵 I I I:
print(np.linalg.inv(D + np.identity(4)))
'''输出如下
[[0.25 0. 0. 0. ][0. 0.5 0. 0. ][0. 0. 0.33333333 0. ][0. 0. 0. 0.33333333]]
'''
得到归一化系数矩阵后,有两种应用方式:
- D ~ − 1 A ~ X W T \tilde D^{-1}\tilde AXW^T D~−1A~XWT 会对每一行特征进行归一化处理。
- A ~ D ~ − 1 X W T \tilde A \tilde D^{-1}XW^T A~D~−1XWT 会对每一列特征进行归一化处理。
接下来,通过计算 D ~ − 1 A ~ \tilde D^{-1}\tilde A D~−1A~ 和 A ~ D ~ − 1 \tilde A \tilde D^{-1} A~D~−1 进行验证:
D ~ − 1 A ~ = [ 1 4 0 0 0 0 1 2 0 0 0 0 1 3 0 0 0 0 1 3 ] ⋅ [ 1 1 1 1 1 1 0 0 1 0 1 1 1 0 1 1 ] = [ 1 4 1 4 1 4 1 4 1 2 1 2 0 0 1 3 0 1 3 1 3 1 3 0 1 3 1 3 ] A ~ D ~ − 1 = [ 1 1 1 1 1 1 0 0 1 0 1 1 1 0 1 1 ] ⋅ [ 1 4 0 0 0 0 1 2 0 0 0 0 1 3 0 0 0 0 1 3 ] = [ 1 4 1 2 1 3 1 3 1 4 1 2 0 0 1 4 0 1 3 1 3 1 4 0 1 3 1 3 ] \tilde D^{-1}\tilde A=\left[\begin{array}{c} \frac 14 & 0 & 0 & 0\\ 0 & \frac 12 & 0 & 0\\ 0 & 0 & \frac 13 & 0\\ 0 & 0 & 0 & \frac 13\\ \end{array}\right] \cdot \left[\begin{array}{c} 1 & 1 & 1 & 1\\ 1 & 1 & 0 & 0\\ 1 & 0 & 1 & 1\\ 1 & 0 & 1 &1\\ \end{array}\right]=\left[\begin{array}{c} \frac 14 & \frac 14 & \frac 14 & \frac 14\\ \frac 12 & \frac 12 & 0 & 0\\ \frac 13 & 0 & \frac 13 & \frac 13\\ \frac 13 & 0 & \frac 13 & \frac 13\\ \end{array}\right]\\ \tilde A \tilde D^{-1}=\left[\begin{array}{c} 1 & 1 & 1 & 1\\ 1 & 1 & 0 & 0\\ 1 & 0 & 1 & 1\\ 1 & 0 & 1 &1\\ \end{array}\right] \cdot \left[\begin{array}{c} \frac 14 & 0 & 0 & 0\\ 0 & \frac 12 & 0 & 0\\ 0 & 0 & \frac 13 & 0\\ 0 & 0 & 0 & \frac 13\\ \end{array}\right]=\left[\begin{array}{c} \frac 14 & \frac 12 & \frac 13 & \frac 13\\ \frac 14 & \frac 12 & 0 & 0\\ \frac 14 & 0 & \frac 13 & \frac 13\\ \frac 14 & 0 & \frac 13 & \frac 13\\ \end{array}\right] D~−1A~= 41000021000031000031 ⋅ 1111110010111011 = 4121313141210041031314103131 A~D~−1= 1111110010111011 ⋅ 41000021000031000031 = 4141414121210031031313103131
在第一种情况下,每一行的和都等于 1;在第二种情况下,每一列的和都等于 1。矩阵乘法可以使用 numpy.matmul() 函数执行,或使用 Python 内置的矩阵乘法运算符 @。定义邻接矩阵并使用 @ 操作符计算矩阵乘法:
A = np.array([[1, 1, 1, 1],[1, 1, 0, 0],[1, 0, 1, 1],[1, 0, 1, 1]
])
print(np.linalg.inv(D + np.identity(4)) @ A)
print('------------------------------')
print(A @ np.linalg.inv(D + np.identity(4)))
'''输出如下
[[0.25 0.25 0.25 0.25 ][0.5 0.5 0. 0. ][0.33333333 0. 0.33333333 0.33333333][0.33333333 0. 0.33333333 0.33333333]]
------------------------------
[[0.25 0.5 0.33333333 0.33333333][0.25 0.5 0. 0. ][0.25 0. 0.33333333 0.33333333][0.25 0. 0.33333333 0.33333333]]
'''
得到的结果与手动计算的矩阵乘法相同。那么,在实践中我们应该使用哪种应用方式?第一种方案似乎看起来合理,因为它能很好地对相邻节点特征进行归一化处理。
但 Kipf 和 Welling 提出,具有多个邻居的节点的特征很容易传播,而与之相反,孤立节点的特征不容易传播。在 GCN 论文中,作者提出了一种混合归一化方法来平衡这种影响。在实践中,使用以下公式为邻居较少的节点分配更高的权重:
H = D ~ − 1 2 A ~ T D ~ − 1 2 X W T H=\tilde D^{-\frac 12}\tilde A^T\tilde D^{-\frac 12}XW^T H=D~−21A~TD~−21XWT
就单个嵌入而言,上式可以写为:
h i = ∑ j ∈ N i 1 deg ( i ) deg ( j ) x j W T h_i=\sum_{j\in \mathcal N_i}\frac 1{\sqrt {\deg(i)}\sqrt {\deg(j)}}x_jW^T hi=j∈Ni∑deg(i)deg(j)1xjWT
这就是实现原始图卷积层的数学公式。与普通的 GNN 层一样,我们可以通过堆叠图卷积层创建 GCN。接下来,使用 PyTorch Geometric 实现一个 GCN 模型,并验证其性能是否优于原始图神经网络模型。
2. 比较 GCN 和 GNN
我们已经证明了 vanilla GNN 性能优于 Node2Vec 模型,接下来,我们将其与 GCN 进行比较,比较它们在 Cora 和 Facebook Page-Page 数据集上的表现。
与普通 GNN 相比,GCN 的主要特点是通过考虑节点度来权衡其特征。在构建模型之前,我们首先计算这两个数据集中的节点度,这与 GCN 的性能直接相关。
根据我们对 GCN 架构的了解,可以猜测当节点度差异较大时,它的性能会更好。如果每个节点都有相同数量的邻居,那么无论使用哪种归一化方式,架构之间都是等价的: deg ( i ) deg ( i ) = deg ( i ) \sqrt {\deg(i)} \sqrt {\deg(i)}= \deg (i) deg(i)deg(i)=deg(i)。
2.1 数据集分析
(1) 从 PyTorch Geometric 中导入 Planetoid 类,为了可视化节点度,同时导入两个附加类( degree 用于获取每个节点的邻居数,Counter 用于计算每个度数的节点数)和 matplotlib 库:
import torch
from torch_geometric.datasets import Planetoid
from torch_geometric.utils import degree
from collections import Counter
import matplotlib.pyplot as plt
(2) 导入 Cora 数据集,并将图存储在 data 中:
dataset = Planetoid(root=".", name="Cora")
data = dataset[0]
(3) 计算图中每个节点的邻居数:
degrees = degree(data.edge_index[0]).numpy()
(4) 为了生成更自然的可视化效果,统计具有相同度的节点数量:
numbers = Counter(degrees)
(5) 使用条形图来绘制统计结果:
fig, ax = plt.subplots()
ax.set_xlabel('Node degree')
ax.set_ylabel('Number of nodes')
plt.bar(numbers.keys(), numbers.values())
plt.show()

从上图中可以看出,图中的度分布近似指数分布,从 1 个邻居( 485 个节点)到 168 个邻居( 1 个节点)不等,这种不平衡的数据集正是归一化处理的用武之地。
(6) 在 Facebook Page-Page 数据集上重复同样的过程:
from torch_geometric.datasets import FacebookPagePage# Import dataset from PyTorch Geometric
dataset = FacebookPagePage(root=".")
data = dataset[0]# Create masks
data.train_mask = range(18000)
data.val_mask = range(18001, 20000)
data.test_mask = range(20001, 22470)# Get list of degrees for each node
degrees = degree(data.edge_index[0]).numpy()# Count the number of nodes for each degree
numbers = Counter(degrees)# Bar plot
fig, ax = plt.subplots()
ax.set_xlabel('Node degree')
ax.set_ylabel('Number of nodes')
plt.bar(numbers.keys(), numbers.values())
plt.show()

Facebook Page-Page 数据集的图的节点度分布看起来更加失衡,邻居数量从 1 到 709 不等。出于同样的原因,Facebook Page-Page 数据集也是应用 GCN 的合适实例。
2.2 实现 GCN 架构
我们可以从零开始实现 GCN 层,但这里我们无需再从头造轮子,PyTorch Geometric 已经内置了 GCN 层,首先在 Cora 数据集上实现 GCN 架构。
(1) 从 PyTorch Geometric 中导入 GCN 层,并导入 PyTorch:
import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConvdataset = Planetoid(root=".", name="Cora")
data = dataset[0]
(2) 创建函数 accuracy() 计算模型准确率:
def accuracy(y_pred, y_true):"""Calculate accuracy."""return torch.sum(y_pred == y_true) / len(y_true)
(3) 创建 GCN 类,其中 __init__() 函数接受三个参数作为输入:输入维度 dim_in、隐藏维度 dim_h 和输出维度 dim_out:
class GCN(torch.nn.Module):"""Graph Convolutional Network"""def __init__(self, dim_in, dim_h, dim_out):super().__init__()self.gcn1 = GCNConv(dim_in, dim_h)self.gcn2 = GCNConv(dim_h, dim_out)
(4) forward() 方法使用两个 GCN 层,并对分类结果应用 log_softmax 函数:
def forward(self, x, edge_index):h = self.gcn1(x, edge_index)h = torch.relu(h)h = self.gcn2(h, edge_index)return F.log_softmax(h, dim=1)
(5) fit() 方法与 Vanilla GNN 相同,为了更好的比较,使用具有相同参数的 Adam 优化器,其中学习率 lr 为 0.1,L2 正则化 weight_decay 为 0.0005:
def fit(self, data, epochs):criterion = torch.nn.CrossEntropyLoss()optimizer = torch.optim.Adam(self.parameters(),lr=0.01,weight_decay=5e-4)self.train()for epoch in range(epochs+1):optimizer.zero_grad()out = self(data.x, data.edge_index)loss = criterion(out[data.train_mask], data.y[data.train_mask])acc = accuracy(out[data.train_mask].argmax(dim=1),data.y[data.train_mask])loss.backward()optimizer.step()if(epoch % 20 == 0):val_loss = criterion(out[data.val_mask], data.y[data.val_mask])val_acc = accuracy(out[data.val_mask].argmax(dim=1),data.y[data.val_mask])print(f'Epoch {epoch:>3} | Train Loss: {loss:.3f} | Train Acc:'f' {acc*100:>5.2f}% | Val Loss: {val_loss:.2f} | 'f'Val Acc: {val_acc*100:.2f}%')
(6) 编写 test() 方法:
@torch.no_grad()def test(self, data):self.eval()out = self(data.x, data.edge_index)acc = accuracy(out.argmax(dim=1)[data.test_mask], data.y[data.test_mask])return acc
(7) 实例化模型并训练 100 个 epoch:
# Create the Vanilla GNN model
gcn = GCN(dataset.num_features, 16, dataset.num_classes)
print(gcn)# Train
gcn.fit(data, epochs=100)
训练过程中的输出结果如下:

(8) 最后,在测试集上对模型进行评估:
acc = gcn.test(data)
print(f'\nGCN test accuracy: {acc*100:.2f}%\n')# GCN test accuracy: 80.30%
重复此实验 100 次,模型的平均准确率为 80.26%(±0.59%),明显 vanilla GNN 模型的平均准确率 74.99%(±1.60%)。
(9) 将同样的模型应用于 Facebook Page-Page 数据集,其平均准确率可以达到 91.78%(±0.31%),同样比 vanilla GNN 的结果( 84.91%(±1.88%) )高出很多:
# Load Facebook Page-Page
dataset = FacebookPagePage(root=".")
data = dataset[0]
data.train_mask = range(18000)
data.val_mask = range(18001, 20000)
data.test_mask = range(20001, 22470)# Train GCN
gcn = GCN(dataset.num_features, 16, dataset.num_classes)
print(gcn)
gcn.fit(data, epochs=100)
acc = gcn.test(data)
print(f'\nGCN test accuracy: {acc*100:.2f}%\n')

下表总结了不同模型在不同数据集上的准确率和标准差:
| MLP | GNN | GCN | |
|---|---|---|---|
| Cora | 53.47%(±1.95%) | 74.99%(±1.60%) | 80.26%(±0.59%) |
| 75.22%(±0.39%) | 84.91%(±1.88%) | 91.78%(±0.31%) |
我们可以将这些性能提升归因于这两个数据集中节点度的分布的不平衡性。通过对特征进行归一化处理,并考虑中心节点及其邻居的数量,GCN 的灵活性得到了极大的提升,可以很好地处理各种类型的图。但节点分类远不是 GCN 的唯一应用,在之后的学习中,我们将看到 GCN 模型的更多新颖应用。
小结
在本节中,我们改进了 vanilla GNN 层,使其能够正确归一化节点特征,这一改进引入了图卷积网络 (Graph Convolutional Network, GCN) 层和混合归一化。在 Cora 和 Facebook Page-Page 数据集上,我们对比了 GCN 架构与 Node2Vec 和 vanilla GNN 之间的性能差异。由于采用了归一化处理,GCN 在这两个数据集中都具有较高的准确率。
系列链接
图神经网络实战(1)——图神经网络(Graph Neural Networks, GNN)基础
图神经网络实战(2)——图论基础
图神经网络实战(3)——基于DeepWalk创建节点表示
图神经网络实战(4)——基于Node2Vec改进嵌入质量
图神经网络实战(5)——常用图数据集
图神经网络实战(6)——使用PyTorch构建图神经网络
相关文章:

图神经网络实战(7)——图卷积网络(Graph Convolutional Network, GCN)详解与实现
图神经网络实战(7)——图卷积网络详解与实现 0. 前言1. 图卷积层2. 比较 GCN 和 GNN2.1 数据集分析2.2 实现 GCN 架构 小结系列链接 0. 前言 图卷积网络 (Graph Convolutional Network, GCN) 架构由 Kipf 和 Welling 于 2017 年提出,其理念是…...

大话设计模式之外观模式
外观模式(Facade Pattern)是一种软件设计模式,旨在提供一个简单的接口,隐藏系统复杂性,使得客户端能够更容易地使用系统。这种模式属于结构型模式,它通过为多个子系统提供一个统一的接口,简化了…...
CAD Plant3D 2024 下载地址及安装教程
CAD Plant3D是一款专业的三维工厂设计软件,用于在工业设备和管道设计领域进行建模和绘图。它是Autodesk公司旗下的AutoCAD系列产品之一,专门针对工艺、石油、化工、电力等行业的设计和工程项目。 CAD Plant3D提供了一套丰富的工具和功能,帮助…...
Intellij IDEA / Android studio 可持续开发笔记
Intellij 的Java/安卓工具链有着一种不可持续性,这种不可持续性体现在多个方面。 首先是不可持续运行。IDEA 使用时间越长,内存占用越大,从不主动释放。运行时间越长,日志越多,从不主动清理。 然后是不完整的开源&am…...
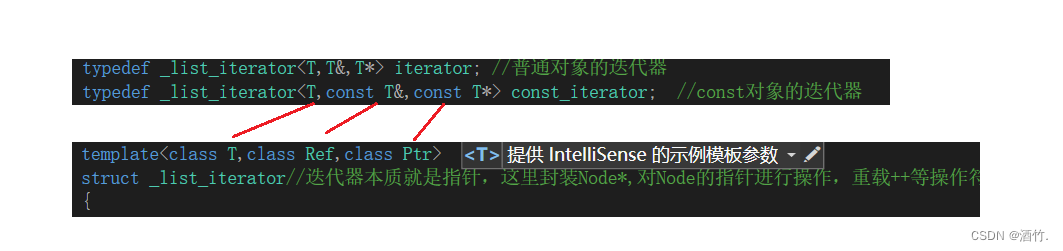
c++----list模拟实现
目录 1. list的基本介绍 2. list的基本使用 2.1 list的构造 用法示例 2.2 list迭代器 用法示例 2.3. list容量(capacity)与访问(access) 用法示例 2.4 list modifiers 用法示例 2.5 list的迭代器失效 3.list的模拟实现 3.1…...

FastAPI+React全栈开发15 让我们构建一个展示API
Chapter03 Getting Started with FastAPI 15 Let’s Build a showcase API FastAPIReact全栈开发15 让我们构建一个展示API REST APIs are all about cycles of HTTP requests and responses, it is the engine that powers the web and is implemented in every web framew…...
容器(二))
list(链表)容器(二)
一、list 插入和删除 函数原型: push_back(elem);//在容器尾部加入一个元素 pop_back();//删除容器中最后一个元素 push_front(elem);//在容器开头插入一个元素 pop_front();//从容器开头移除第一个元素 insert(pos,elem);//在pos位置插elem元素的拷贝,…...

世优科技上榜2024年度《中国虚拟数字人影响力指数报告》
日前,第三期《中国虚拟数字人影响力指数报告》在中国网络视听大会上正式发布。本期《报告》由中国传媒大学媒体融合与传播国家重点实验室(以下简称“国重实验室”)、中国传媒大学数字人研究院编制,中国网络视听协会、人民日报智慧…...

【调试方法】C代码中dump中间数据的方法
一,简介 本文主要介绍,如何在C语言代码中将音频流数据进行写入文件,方便调试定位问题: 二,函数实现 按int8_t写入 #include <stdio.h>int32_t write_int8_t_data(int8_t *name, int8_t *buffer, int32_t dat…...

【BUG】vue中@change时间传值丢失问题
项目场景: 在修改项目bug时,发现后端响应到前端的值,通过change事件调用方法,在方法中拿到值时,有部分数据丢失。 问题描述 后端传到前端的值为:字符串类型的"00000089",change调用…...
Linux提权!!!
上一篇文章讲了Windows的提权,那么这篇文章就来讲一下Linux的提权 1.SUID提权 suid权限 作用:让普通用户临时拥有该文件的属主的执行权限,suid权限只能应用在二进制可执行文件(命令)上,而且suid权限只能设置…...

Android Studio学习7——常用控件view
Android控件 双击shift键——>搜索想要找的文件 Ctrlshift回车——>补全“;”号 CtrlX——>删除一行,只需把鼠标放在那一行 windows自带字体...
)
Springboot3 集成knife4j(swagger)
knife4j是为Java MVC框架集成Swagger生成Api文档的增强解决方案,前身是swagger-bootstrap-ui,取名kni4j是希望它能像一把匕首一样小巧,轻量,并且功能强悍! 官网地址: Knife4j 集Swagger2及OpenAPI3为一体的增强解决方案. | Knife4j 本文以Springboot3版本集成kn…...
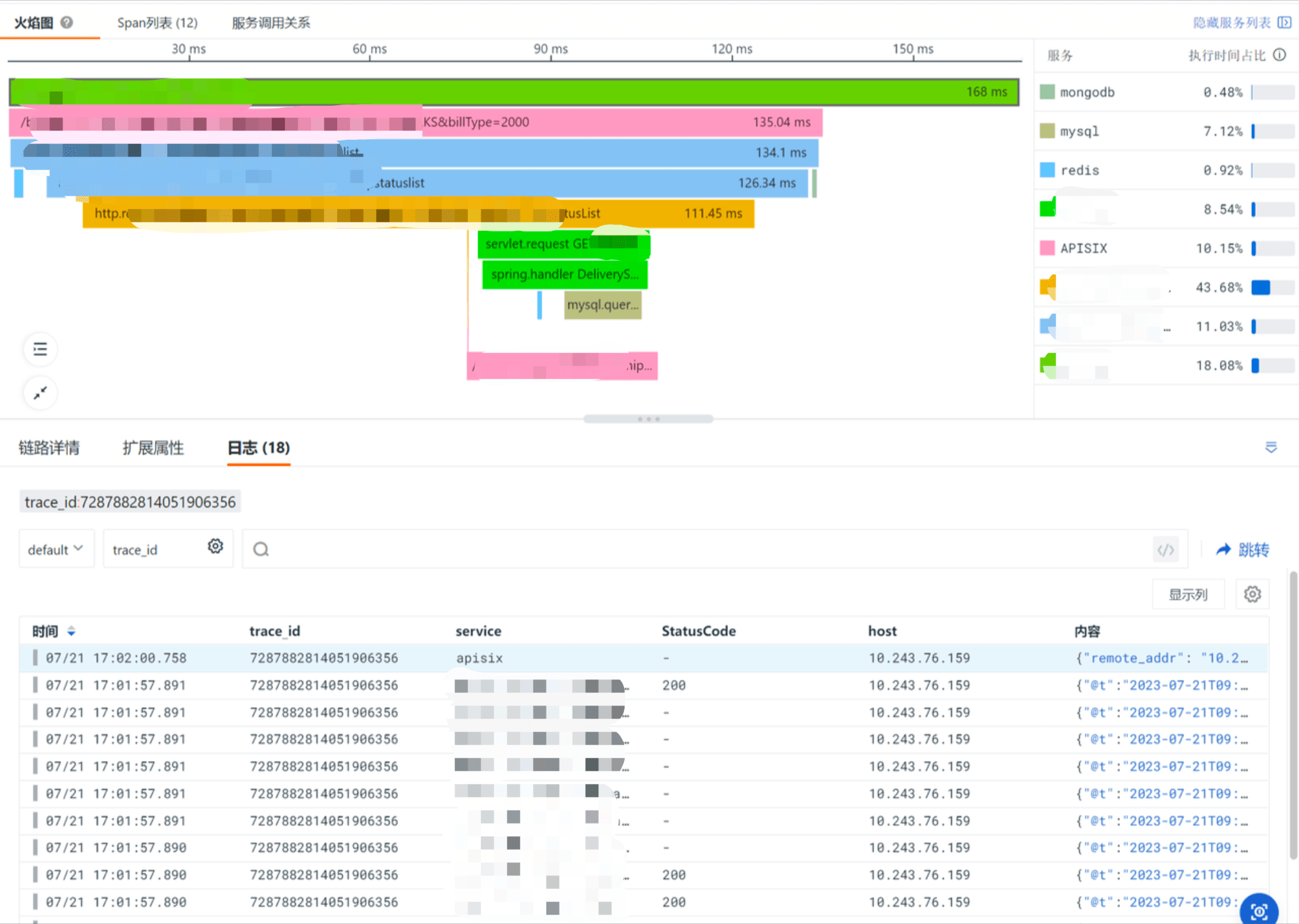
深信服:借助观测云实现全链路可观测性
导读 深信服科技股份有限公司 简称「深信服」( Sangfor Technologies Inc. ),是一家领先的网络安全和云计算解决方案提供商,致力于为全球客户提供高效、智能、安全的网络和云服务。随着公司业务的不断扩展,也面临着监…...

详解Qt中使用线程
详解Qt中使用线程 Qt中的线程相关知识涵盖了线程创建、管理、通信以及线程安全等方面。下面将详细讲解这些知识点,并提供对应的示例代码。 线程创建与管理 QThread类 Qt通过QThread类来创建和管理线程。要创建一个新的工作线程,通常有两种方法&#…...
在.Net6中用gdal实现第一个功能
目录 一、创建.NET6的控制台应用程序 二、加载Gdal插件 三、编写程序 一、创建.NET6的控制台应用程序 二、加载Gdal插件 Gdal的资源可以经过NuGet包引入。右键单击项目名称,然后选择 "Manage NuGet Packages"(管理 NuGet 包)。N…...

采用大语言模型进行查询重写——Query Rewriting via Large Language Models
文章:Query Rewriting via Large Language Models,https://arxiv.org/abs/2403.09060 摘要 查询重写是在将查询传递给查询优化器之前处理编写不良的查询的最有效技术之一。 手动重写不可扩展,因为它容易出错并且需要深厚的专业知识。 类似地…...

使用Vue实现CSS过渡和动画
01-初识动画和过渡 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>使用vue实现css过渡和动画&l…...

一家购物商场的数据运营挑战
✅作者简介:《数据运营:数据分析模型撬动新零售实战》作者、《数据实践之美》作者、数据科技公司创始人、多次参加国家级大数据行业标准研讨及制定、高端企培合作讲师。 🌸公众号:风姑娘的数字视角,免费分享数据应用相…...
React Native框架开发APP,安装免费的图标库(react-native-vector-icons)并使用详解
一、安装图标库 要使用免费的图标库,你可以使用 React Native Vector Icons 库。 首先,确保你已经安装了 react-native-vector-icons: npm install --save react-native-vector-iconsnpm install --save-dev types/react-native-vector-ic…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

【深尚想】TPS54618CQRTERQ1汽车级同步降压转换器电源芯片全面解析
1. 元器件定义与技术特点 TPS54618CQRTERQ1 是德州仪器(TI)推出的一款 汽车级同步降压转换器(DC-DC开关稳压器),属于高性能电源管理芯片。核心特性包括: 输入电压范围:2.95V–6V,输…...
