力扣贪心算法--第一天
前言
今天是贪心算法的第一天,算法之路重新开始!
内容
之前没了解过贪心算法。
什么是贪心
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。难点就是如何通过局部最优,推出整体最优。
一、455.分发饼干
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
思路:
大饼干可以满足胃口大的,也可以满足胃口小的,应该优先满足胃口大的。
这里的局部最优就是大饼干喂给胃口大的,全局最优就是喂饱尽可能多的小孩。
先将饼干数组和小孩数组排序,然后从后向前遍历小孩数组,如果饼干的大小大于或等于孩子的为空则给与,否则不给予,继续寻找选一个饼干是否符合。
func findContentChildren(g []int, s []int) int {sort.Ints(g)sort.Ints(s)child:=0for sIdx:=0;sIdx<len(s)&&child<len(g);sIdx++{if s[sIdx]>=g[child]{child++}}return child
}二、376. 摆动序列
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
-
例如,
[1, 7, 4, 9, 2, 5]是一个 摆动序列 ,因为差值(6, -3, 5, -7, 3)是正负交替出现的。 - 相反,
[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
思路:
将数组用坡度表示出来,
局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。
整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。
但本题要考虑三种情况:
- 情况一:上下坡中有平坡
- 情况二:数组首尾两端
- 情况三:单调坡中有平坡
func wiggleMaxLength(nums []int) int {n:=len(nums)if n<2{return n}ans:=1preDiff:=nums[1]-nums[0]if preDiff!=0{ans=2}for i:=2;i<n;i++{diff:=nums[i]-nums[i-1]if preDiff<=0&&diff>0||preDiff>=0&&diff<0{ans++preDiff=diff}}return ans
}三、53. 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组是数组中的一个连续部分。
思路:
负数只会拉低总和。
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
全局最优:选取最大“连续和”
局部最优的情况下,并记录最大的“连续和”,可以推出全局最优。
func maxSubArray(nums []int) int {maxNum:=nums[0]for i:=1;i<len(nums);i++{if nums[i]+nums[i-1]>nums[i]{nums[i]+=nums[i-1]}if nums[i]>maxNum{maxNum=nums[i]}}return maxNum
}最后
可预见的正在变好!加油!
相关文章:

力扣贪心算法--第一天
前言 今天是贪心算法的第一天,算法之路重新开始! 内容 之前没了解过贪心算法。 什么是贪心 贪心的本质是选择每一阶段的局部最优,从而达到全局最优。难点就是如何通过局部最优,推出整体最优。 一、455.分发饼干 假设你是一…...
Nginx反向代理和缓存
一、Nginx反向代理 1.调度和代理的区别: 1.调度基于内核层面,代理基于应用层面 2.代理必须实现一手托两家 3.调度不需要监听任何端口,不需要工作任何应用程序,代理需要工作和上游服务器一模一样的进程 4.调度没有并发上限&am…...

支持多元AI场景应用,宁畅“NEX AI Lab”开放试用预约中
3月29日,宁畅在京举行发布会,正式发布“全局智算”战略,并在会上推出战略性新品“AI算力栈”,旨在有效解决大模型产业落地的全周期问题。 据宁畅CTO赵雷介绍,“AI算力栈”集成了宁畅在AI计算领域的软硬件能力ÿ…...

Git 如何合并多个连续的提交
我平常的编程喜欢是写一段代码就提交一次,本地一般不攒代码,生怕本地有什么闪失导致白干。但这样就又导致一个问题:查看历史日志时十分不方便,随便找一段提交可以看到: > git log --oneline 8f06be5 add 12/qemu-h…...

k8s 基础入门
1.namespace k8s中的namespace和docker中namespace是两码事,可以理解为k8s中的namespace是为了多租户,dockers中的namespace是为了网络、资源等隔离 2.deployment kubectl create #新建 kubectl aply #新建 更新 升级: 滚动升级&#x…...
【Python项目】AI动物识别工具
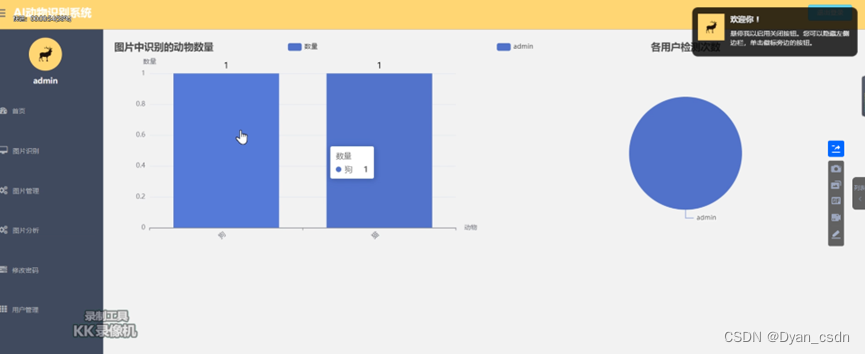
目录 背景 技术简介 系统简介 界面预览 背景 成像技术在全球科技发展中扮演了关键角色。在科学研究领域,拍摄所得的图像成为了一种不可或缺的研究工具。特别是在生态学与动物学研究中,鉴于地球的广阔地域和多样的气候条件,利用图像技术捕…...
详解)
逻辑回归(Logistic Regression)详解
逻辑回归是一种用于解决二分类问题的统计方法,它通过构建一个模型来预测某个事件的概率。 以下是逻辑回归的一些关键要点: 适用场景:逻辑回归特别适合于处理二分类问题,即两个类别的分类问题,例如判断一封邮件是否为…...

.vimrc文件的语句语法
本文结构: a、简介 b、详细解释其中的一些常见语句和语法。 a、.vimrc 文件是 Vim 编辑器用于配置用户设置和自定义行为的文件。当 Vim 启动时,它会读取 .vimrc 文件中的命令和设置,并根据这些指令来配置编辑器的行为。 b、.vimrc 文件中…...

c语言之函数指针作形参
在一些c语言的大工程中,会在定义的函数中,把一些其他函数指针作为本函数形参。 函数指针作形参的例子 代码如下: #include<stdio.h> int max(int a,int b) { return(a>b?a:b); } int min(int a,int b) { return(a<b?a:b); } i…...

python文件的读取操作
打开文件 fopen("F:/python/helloworld/测试.txt","r",encoding"UTF-8")读取文件 print(f"读取10个字节的结果{f.read(10)}") print(f"读取全部字节的结果{f.read()}") linesf.readlines() print(f"{lines}")读…...

查看并设定【网络适配器】的优先级(跃点数)
目录 前言: 1.查看所有的适配器 2.修改优先级(需要以管理员身份运行) 跃点数(InterfaceMetric ) DHCP 3.修改后的效果 pwoerShell 再次运行之前的程序 4.其他 参考 网络适配器1,8相关知识介绍1 …...
深入理解 Hadoop 上的 Hive 查询执行流程
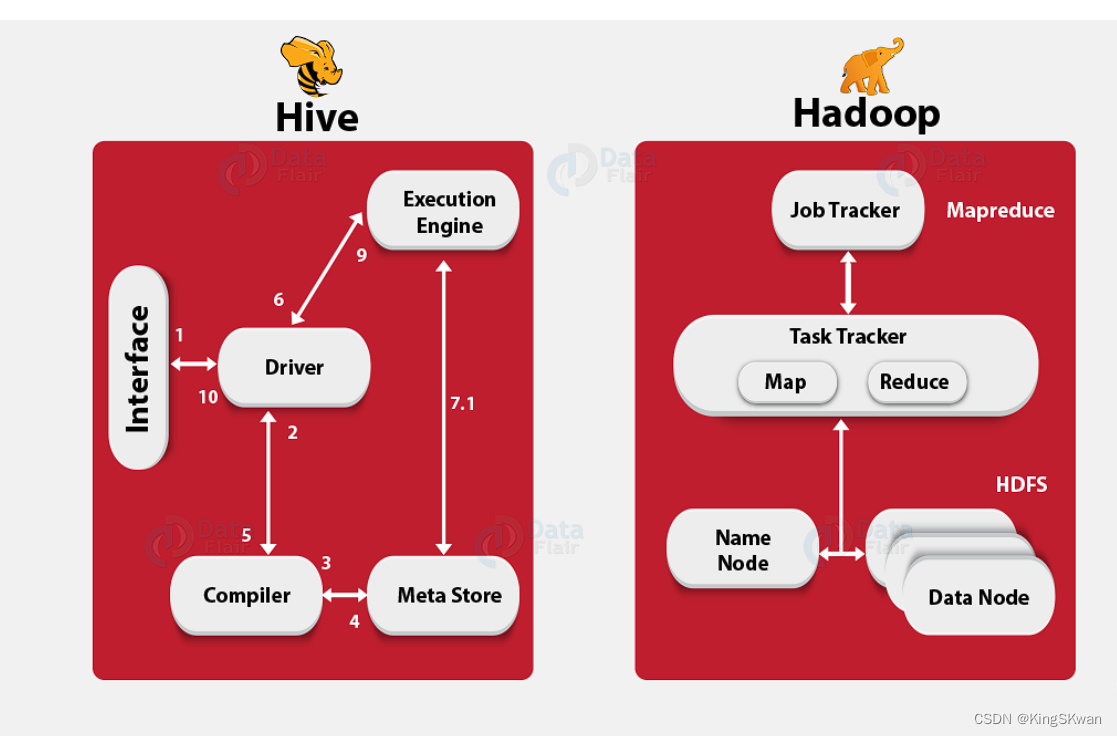
在 Hadoop 生态系统中,Hive 是一个重要的分支,它构建在 Hadoop 之上,提供了一个开源的数据仓库系统。它的主要功能是查询和分析存储在 Hadoop 文件中的大型数据集,包括结构化和半结构化数据。Hive 在数据查询、分析和汇总方面发挥…...

JS封装网页进入/退出全屏功能,兼容各大主流浏览器
1、演示 2、封装进入全屏函数 mozRequestFullScreen:兼容Firefox webkitRequestFullscreen:兼容 Chrome、Safari、Opera msRequestFullscreen:兼容:IE/Edge const enter () > {const element document.documentElementif (el…...

el-table的复选框勾选整行变色
要实现el-table的复选框勾选整行变色,你可以使用element-ui提供的row-class-name属性结合scoped slot来完成。 首先,你需要为el-table组件添加 row-class-name 属性,并给它绑定一个方法。在这个方法中,你可以根据你的业务逻辑来判…...

一步一步写线程之八线程池的完善之二数据结构封装
一、数据容器 在前面分析过,不管是线程任务的封装还是同步数据队列的封装,都是需要一个数据结构的。一用来说,如果没有什么特殊的原因,开发者都是使用STL中数据结构。比如前面经常见到的std::queue,std::deque,std::vector,std::…...

go连接数据库(原生)
根据官网文档 Go Wiki: SQL Database Drivers - The Go Programming Language 可以看到go可以连接的关系型数据库 常用的关系型数据库基本上都支持,下面以mysql为例 下载mysql驱动 打开上面的mysql链接 GitHub - go-sql-driver/mysql: Go MySQL Driver i…...
【C语言】2048小游戏【附源码】
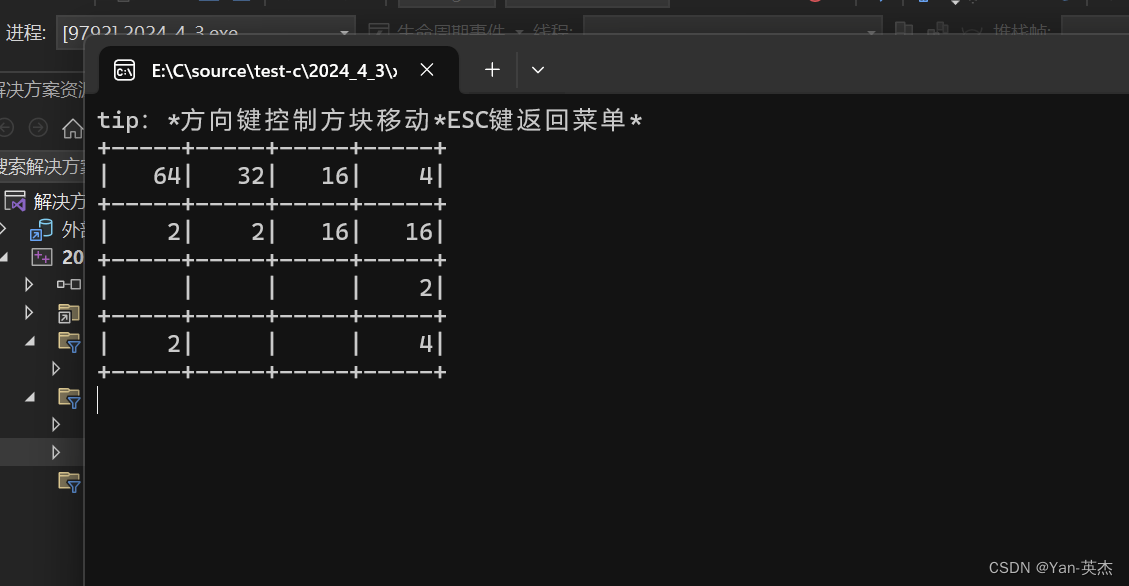
欢迎来到英杰社区https://bbs.csdn.net/topics/617804998 一、游戏描述: 2048是一款数字益智类游戏,玩家需要使用键盘控制数字方块的移动,合并相同数字的方块,最终达到数字方块上出现“2048”的目标。 每次移动操作,所…...
部署项目遇到的各种问题总结
文章目录 前言一、后端问题 jar包运行出现错误宝塔面板使用jdk17二、数据库问题 版本问题三、前端问题 连不上后端总结 前言 在做完项目之后,为了让别人访问到自己的网站,就需要部署前端后端以及数据库,但是在部署的过程中出现了各种问题和困…...
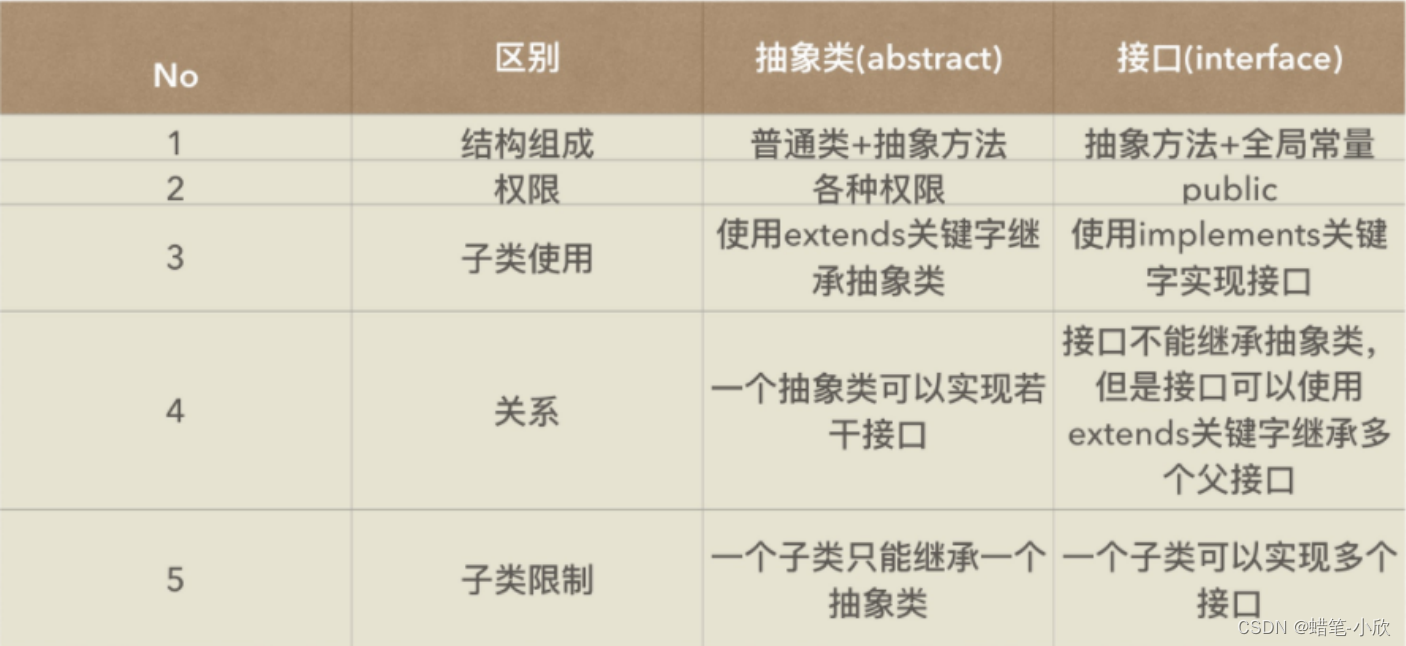
JavaSE:抽象类和接口
目录 一、前言 二、抽象类 (一)抽象类概念 (二)使用抽象类的注意事项 (三)抽象类的作用 三、接口 (一)接口概念 (二)接口语法规则 (三&a…...

发票是扫码验真好,还是OCR后进行验真好?
随着科技的进步,电子发票的普及使得发票的验真方式也在不断演进。目前,我们常见的发票验真方式主要有两种:一种是扫描发票上的二维码进行验真,另一种是通过OCR(Optical Character Recognition,光学字符识别…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
