计算机视觉之三维重建(6)---多视图几何(上)
文章目录
- 一、运动恢复结构问题(SfM)
- 二、欧式结构恢复
- 2.1 概述
- 2.2 求解
- 2.3 欧式结构恢复歧义
- 三、仿射结构恢复
- 3.1 概述
- 3.2 因式分解法
- 3.3 总结
- 3.4 仿射结构恢复歧义
一、运动恢复结构问题(SfM)
1. 运动恢复结构问题:通过三维场景的多张图像,恢复出该场景的三维结构信息以及每张图片对应的摄像机参数。

2. 运动恢复问题建模表述:已知 n n n 个世界坐标点在 m m m 张图像中的对应点的像素坐标 x i j x_{ij} xij,计算出 m m m 个摄像机的投影矩阵 M i M_i Mi 和 n n n 个三维点 X j X_j Xj 的坐标。下图中 M = K [ R , T ] M=K[R,T] M=K[R,T]。

二、欧式结构恢复
2.1 概述
1. 欧式结构恢复问题:摄像机内参数已知,外参数未知情况。
2. 对于欧式结构恢复问题,已知摄像机内参数,根据投影矩阵的计算公式可知 x i j = M i X j = K i [ R i , T i ] X j x_{ij}=M_iX_j=K_i[R_i,T_i]X_j xij=MiXj=Ki[Ri,Ti]Xj。那么求解投影矩阵 M M M 只需要求解外参数 [ R , T ] [R,T] [R,T]。

2.2 求解
1. 对于二视图的欧式结构恢复问题,如果把世界坐标系放在第一个坐标系下面,那摄像机 1 1 1 的外参数为 [ I , 0 ] [I,0] [I,0],而摄像机 2 2 2 的外参数 [ R , T ] [R,T] [R,T] 却是未知的。

2. 求解步骤:
(1)求解基础矩阵 F F F(归一化八点法)
(2)求解本质矩阵 E = K 2 T F K 1 E=K_2^TFK_1 E=K2TFK1
(3)分解本质矩阵 E → R , T E \rightarrow R,T E→R,T
(4)三角化(求解世界坐标系下的3D坐标)

3. 上面步骤中除了分解本质矩阵 E E E 外,其他都在之前文章中提到过。分解本质矩阵 E E E 在编程下的代码不难,但是推导过程极其复杂,博主在这里就不叙述了。
import numpy as np # 假设你已经有了一个本质矩阵E
E = np.array([[...], [...], [...]]) # 用你的本质矩阵替换这里的占位符 # 对E进行奇异值分解
U, S, Vt = np.linalg.svd(E) # 根据SVD分解的结果恢复旋转矩阵R和平移向量t
W = np.array([[0, -1, 0], [1, 0, 0], [0, 0, 1]])
R1 = U @ W @ Vt
R2 = U @ W.T @ Vt # 由于t的方向是不确定的,我们通常选择使t的最后一个分量为正的那个解
t1 = U[:, 2]
t2 = -U[:, 2] # 选择合适的R和t组合
if np.linalg.det(R1) * np.linalg.det(np.eye(3) - R1) < 0: R, t = R2, t2
else: R, t = R1, t1 # 现在你有了旋转矩阵R和平移向量t
print("Rotation matrix R:")
print(R)
print("Translation vector t:")
print(t)
2.3 欧式结构恢复歧义
1. 在没有先验信息的情况下,我们求解出来的解跟真实解是存在一个相似变换关系(旋转、平移、缩放)。
2. 度量重构:恢复的场景与真实场景之间仅存在相似变换的重构。如果欧式结构恢复后能达到这种重构的话,那就可以说的上恢复效果是很不错了。


三、仿射结构恢复
3.1 概述
1. 仿射结构恢复问题:摄像机为仿射相机,内外参数均未知。 一般来说仿射相机代表为弱透视投影摄像机。
2. 下面图中所有坐标使用欧式坐标,对于仿射变换而言 z z z 轴的 m 3 X = 1 m_3X=1 m3X=1,所以经过等式变换世界坐标的欧式坐标与像平面欧式坐标关系为 x E = A X E + b x^E=AX^E+b xE=AXE+b。其中 A 2 ∗ 3 , b 2 ∗ 1 A_{2∗3},b_{2∗1} A2∗3,b2∗1。

3. 仿射结构恢复问题可以建模为:已知 n n n 个三维点 X j X_j Xj 在 m m m 张图像中的对应点的像素坐标为 x i j x_{ij} xij,且 x i j = A i X j + b i x_{ij}=A_iX_j+b_i xij=AiXj+bi,其中第 i i i 张图片对应的仿射相机的投影矩阵为 M i M_i Mi。求解 n n n 个三维点 X j X_j Xj 的坐标以及 m m m 个仿射相机的投影矩阵中的 A i A_i Ai, b i b_i bi ( i = 1 , 2 , . . . , m i=1,2,...,m i=1,2,...,m)。

3.2 因式分解法
1. 数据中心化:对于所有像平面点和世界坐标的三维点,分别减去像平面点和三维点的质心,建立新的关系,可知 x ^ i j = A i X ^ j \widehat{x}_{ij}=A_i\widehat{X}_j x ij=AiX j。其中 x ^ i j = x i j − x ˉ i j \widehat{x}_{ij}=x_{ij}-\bar{x}_{ij} x ij=xij−xˉij, X ^ j = X j − X ˉ j \widehat{X}_j=X_j-\bar{X}_j X j=Xj−Xˉj。通过数据中心化消掉了 b b b 的影响。
2. 如果3D点的质心=世界坐标系的中心,那么减去的均值为 0 0 0,所以 x ^ i j = A i X j \widehat{x}_{ij}=A_i{X}_j x ij=AiXj。

3. 矩阵形式如下所示。接下来我们要将 D 2 m ∗ n D_{2m*n} D2m∗n 分解为 M 2 m ∗ 3 M_{2m*3} M2m∗3 和 S 3 ∗ n S_{3*n} S3∗n,即因式分解。


4. 由于 M M M 和 S S S 的秩为 3 3 3,所以 D D D 的秩为 3 3 3,我们对 D 2 m ∗ n D_{2m*n} D2m∗n 矩阵进行奇异值分解。可以得到 D 2 m ∗ n = U 2 m ∗ 3 × W 3 ∗ 3 × V 3 ∗ n D_{2m*n}=U_{2m*3} \times W_{3*3} \times V_{3*n} D2m∗n=U2m∗3×W3∗3×V3∗n。


3.3 总结

3.4 仿射结构恢复歧义
1. 仿射结构恢复歧义:投影矩阵存在一个可逆 3 ∗ 3 3*3 3∗3 矩阵的变换,也就是差了一个仿射变换的矩阵系数。对于歧义我们需要引入其他约束来解决歧义。

2. 另外对于给定 m m m 个相机, n n n 个 3 3 3 维点情况下,我们将有 2 m n 2mn 2mn 个等式, 8 m + 3 n − 8 8m+3n-8 8m+3n−8 个未知量。

相关文章:

计算机视觉之三维重建(6)---多视图几何(上)
文章目录 一、运动恢复结构问题(SfM)二、欧式结构恢复2.1 概述2.2 求解2.3 欧式结构恢复歧义 三、仿射结构恢复3.1 概述3.2 因式分解法3.3 总结3.4 仿射结构恢复歧义 一、运动恢复结构问题(SfM) 1. 运动恢复结构问题:通…...
(栈溢出的处理办法))
蓝桥杯:全球变暖(python,BFS,DFS)(栈溢出的处理办法)
图论的经典题型,深度优先搜索和广度优先搜索都可以,但是本题推荐使用广度优先搜索(类似的题最好都用广度优先搜索),因为使用深度优先搜索会爆栈(栈溢出)。本篇博客两种方法都进行讲解࿰…...

Qt C++ | Qt 元对象系统、信号和槽及事件(第一集)
01 元对象系统 一、元对象系统基本概念 1、Qt 的元对象系统提供的功能有:对象间通信的信号和槽机制、运行时类型信息和动态属性系统等。 2、元对象系统是 Qt 对原有的 C++进行的一些扩展,主要是为实现信号和槽机制而引入的, 信号和槽机制是 Qt 的核心特征。 3、要使用元…...

Python 抽象类
在Python的抽象基类(ABC)中,方法并不是必须全部是抽象方法。抽象基类可以同时包含抽象方法和具体方法。抽象类中可以有抽象方法也可以定义具体方法 具体来说: 抽象方法: 使用abc.abstractmethod装饰器标记的方法是抽象方法。抽象方法没有方法体,只有方法签名。抽象方法必须在具…...
达梦数据库自动备份(全库)+还原(全库) 控制台
一 前提 1.安装达梦数据库DB8(请参照以前文章) 我的数据库安装目录是 /app/dmDB8 2.已创建实例 (请参照上一篇文章) 二 准备测试数据 三 自动备份步骤 1.开启归档模式 开启DM管理工具管理控制台 弹不出来工具的 输入命令 xhost 第一步 将服务器转换为配置状态 右键-&g…...
)
android AndroidAutoSize 取消第三方库适配问题(两个步骤)
比如第三方库的Activity是:PictureSelectorSupporterActivity、PictureSelectorTransparentActivity、CropImageActivity 1.在自定义Application 的 onCreate 方法设置: Overridepublic void onCreate() {super.onCreate();this.mAppthis;registerActi…...
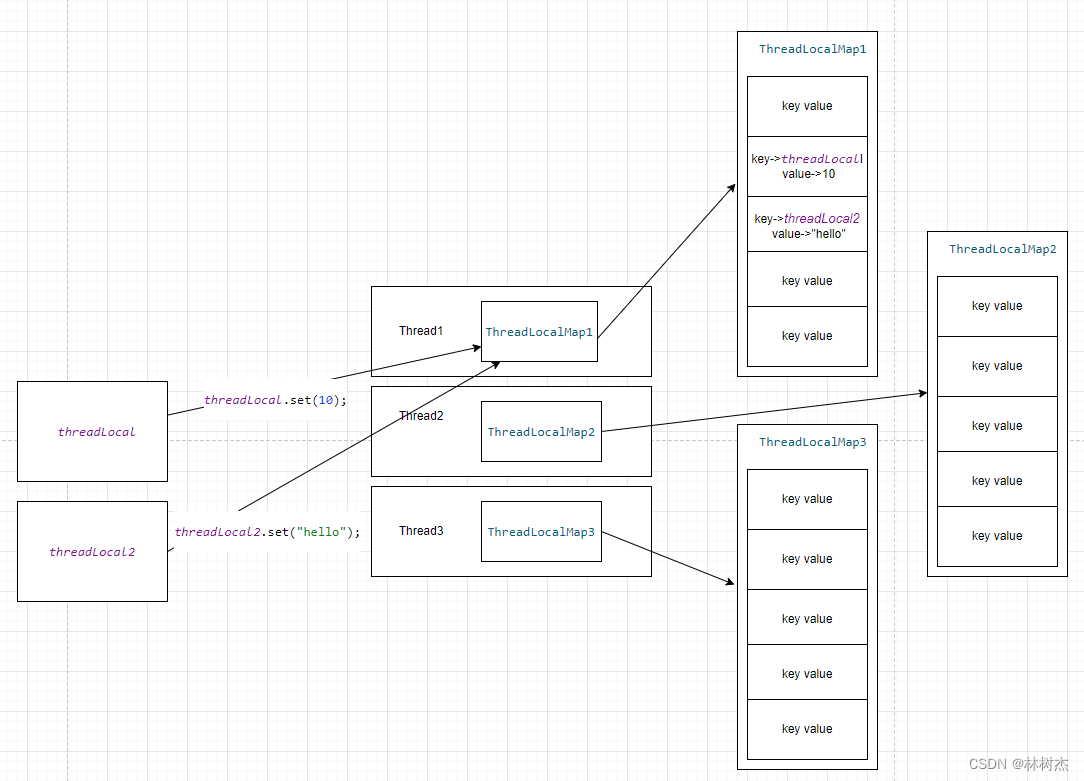
【Java 多线程】从源码出发,剖析Threadlocal的数据结构
文章目录 exampleset(T value)createMap(t, value);set(ThreadLocal<?> key, Object value)ThreadLocalMap和Thread的关系 全貌 ThreadLocal是个很重要的多线程类,里面数据结构的设计很有意思,很巧妙。但是我们平时使用它的时候常常容易对它的使用…...
Sy6 编辑器vi的应用(+shell脚本3例子)
实验环境: 宿主机为win11,网络:10.255.50.5 6389 WSL2 ubuntu 目标机的OS:Ubuntu 内核、版本如下: linuxpeggy0223:/$ uname -r 5.15.146.1-microsoft-standard-WSL2 linuxpeggy0223:/$ cat /proc/version Linux vers…...
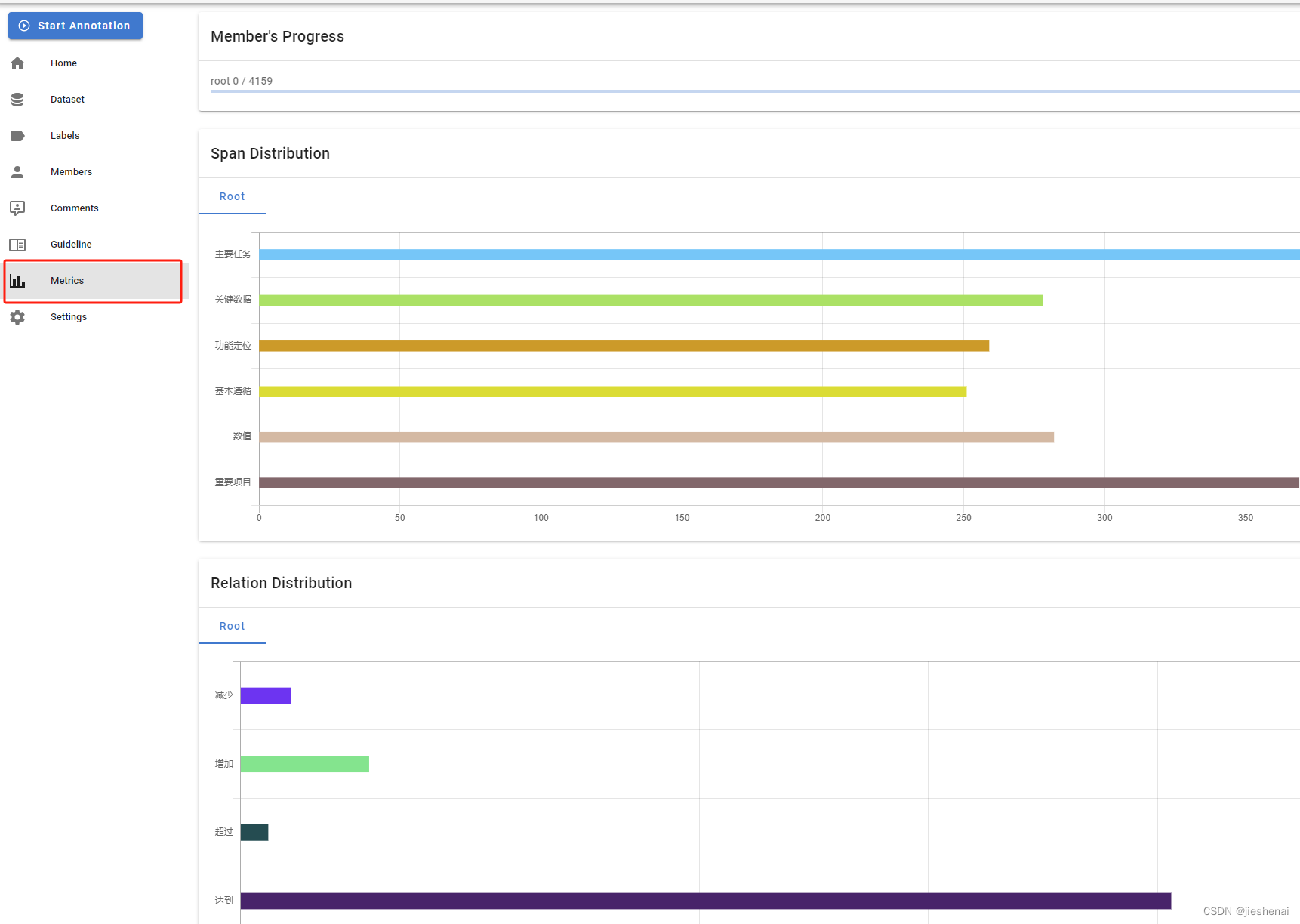
把标注数据导入到知识图谱
文章目录 简介数据导入Doccano标注数据,导入到Neo4j寻求帮助 简介 团队成员使用 Doccano 标注了一些数据,包括 命名实体识别、关系和文本分类 的标注的数据; 工作步骤如下: 首先将标注数据导入到Doccano,查看一下标注…...

【前端基础】什么是类数组对象,类数组对象转换成数组的方法
类数组对象(array-like object)是指在 JavaScript 中具有类似数组的特征但不是真正的数组的对象。这些对象具有类似数组的特性,例如有一个 length 属性和通过索引访问元素的能力,但它们不具备数组对象的所有方法和特性。 什么是类…...
Python快速入门系列-8(Python数据分析与可视化)
第八章:Python数据分析与可视化 8.1 数据处理与清洗8.1.1 数据加载与查看8.1.2 数据清洗与处理8.1.3 数据转换与整理8.2 数据可视化工具介绍8.2.1 Matplotlib8.2.2 Seaborn8.2.3 Plotly8.3 数据挖掘与机器学习简介8.3.1 Scikit-learn8.3.2 TensorFlow总结在本章中,我们将探讨…...

双非硕转测试之Java学习笔记(一):集合
Java学习-----集合 简单概括单列集合--collectionlist接口:vector类:LinkedList类:set接口:HasSet类:LinkedHashSet类: 双列集合--MapMap接口:HashMap类:HashTable类:Pro…...

zabbix源码安装
目录 一.安装php和nginx客户端环境 二.修改php配置 三.修改nginx配置文件 四.下载并编译zabbix 五.创建zabbix需要的用户及组 六.安装编译需要的依赖 七.配置zabbix文件 八.数据库配置 九.配置zabbix 十.web界面部署 十一.遇到无法创建配置文件 十二.登录zabbix 前…...

计算机视觉之三维重建(5)---双目立体视觉
文章目录 一、平行视图1.1 示意图1.2 平行视图的基础矩阵1.3 平行视图的极几何1.4 平行视图的三角测量 二、图像校正三、对应点问题3.1 相关匹配法3.2 归一化相关匹配法3.3 窗口问题3.4 相关法存在的问题3.5 约束问题 一、平行视图 1.1 示意图 如下图即是一个平行视图。特点&a…...

计算机网络-TCP/IP 网络模型
TCP/IP网络模型各层的详细描述: 应用层:应用层为应用程序提供数据传输的服务,负责各种不同应用之间的协议。主要协议包括: HTTP:超文本传输协议,用于从web服务器传输超文本到本地浏览器的传送协议。FTP&…...

算法训练营第29天|LeetCode 491.递增子序列 46.全排列 47.全排列Ⅱ
LeetCode 491.递增子序列 题目链接: LeetCode 491.递增子序列 解题思路: 用哈希集合进行去重,同一树层不能取重复元素。 代码: class Solution { public:vector<vector<int>>result;vector<int>path;void…...

Ubuntu服务器搭建 - 环境篇
Ubuntu服务器搭建 - 环境篇 基于腾讯云服务器 - Ubuntu 20.04 LTS 一、安装 - MySQL 1.1 概述 MySQL安装方式有三种: 1. 使用Ubuntu 包管理工具 apt安装 2. 使用MySQL官方APT存储库安装 3. 使用MySQL官方二进制发行版安装 1.2 安装 MySQL 使用MySQL官方APT存储库安装 $ wget…...

深度学习基础模型之Mamba
Mamba模型简介 问题:许多亚二次时间架构(运行时间复杂度低于O(n^2),但高于O(n)的情况)(例如线性注意力、门控卷积和循环模型以及结构化状态空间模型(SSM))已被开发出来,以解决 Transformer 在长…...

Topaz Video AI for Mac v5.0.0激活版 视频画质增强软件
Topaz Video AI for Mac是一款功能强大的视频处理软件,专为Mac用户设计,旨在通过人工智能技术为视频编辑和增强提供卓越的功能。这款软件利用先进的算法和深度学习技术,能够自动识别和分析视频中的各个元素,并进行智能修复和增强&…...

解决WordPress文章的段落首行自动空两格的问题
写文章时,段落首行都会空两格,可是WordPress自带的编辑器却没有考虑到这一点,导致发布的文章首行都是顶格的,看起来很不习惯。 我们通常的解决方法都是在发布文章时把编辑器切换到“文本”模式,然后再在首行手动键入两…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...
