(文章复现)考虑分布式电源不确定性的配电网鲁棒动态重构
参考文献:
[1]徐俊俊,吴在军,周力,等.考虑分布式电源不确定性的配电网鲁棒动态重构[J].中国电机工程学报,2018,38(16):4715-4725+4976.
1.摘要
间歇性分布式电源并网使得配电网网络重构过程需要考虑更多的不确定因素。在利用仿射数对分布式电源出力的不确定性进行合理分析与建模基础上,建立以重构周期内开关动作耗费与网络有功损耗等综合成本最低为目标函数,以网络安全运行为约束条件的配电网鲁棒动态重构模型。为精确求解该数学模型,引入基于最佳等距思想的分段线性逼近方法将原目标函数松弛为线性可解形式,并根据对偶定理将模型进一步等效转化为双层混合整数线性规划问题;最后采用列约束生成算法对模型进行高效求解。修改的 PG&E 69节点系统测试分析结果表明,与现有的配电网确定性动态重构方法比较,所提鲁棒动态重构方法在抗系统不确定性扰动方面具有明显的优势。
2.原理介绍
2.1分布式电源出力区间预测
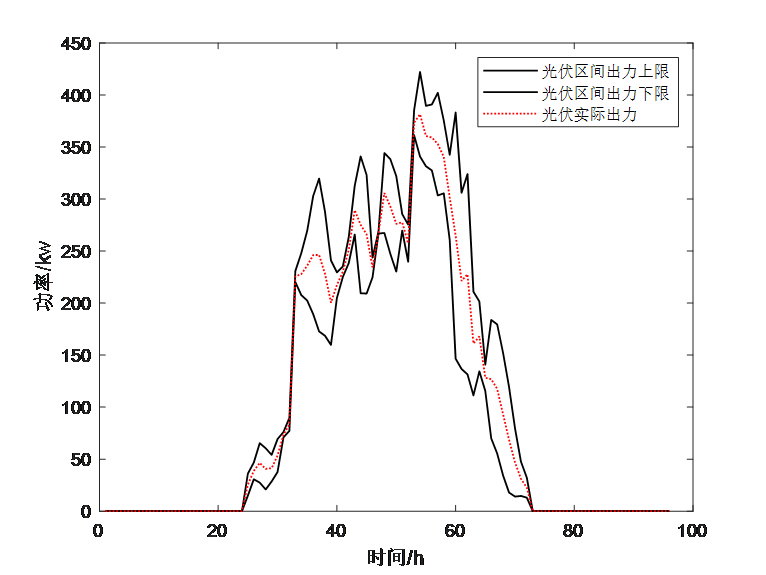
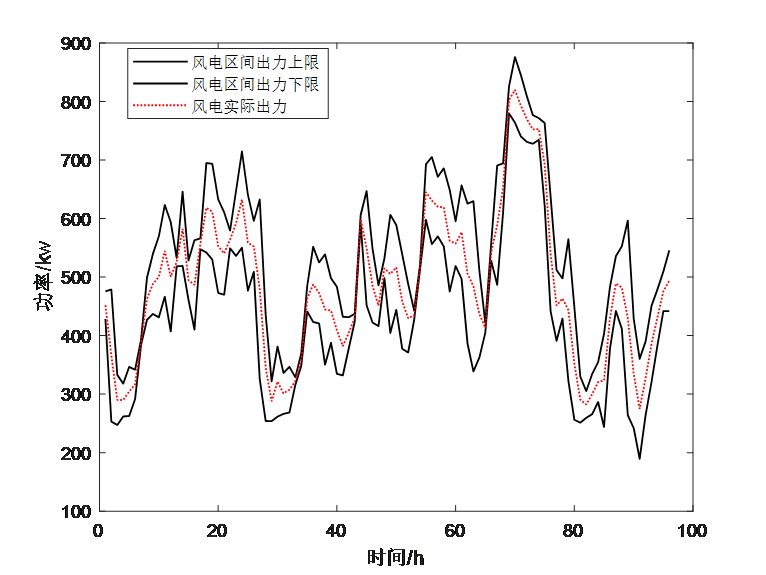
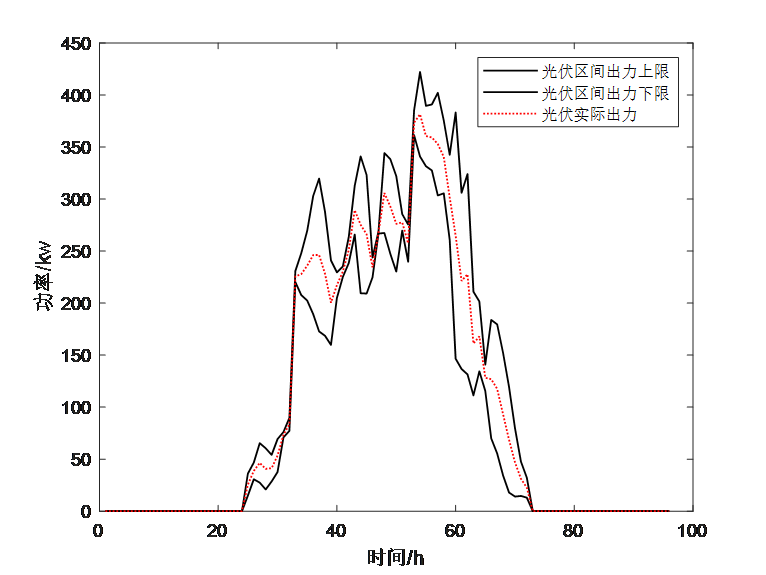
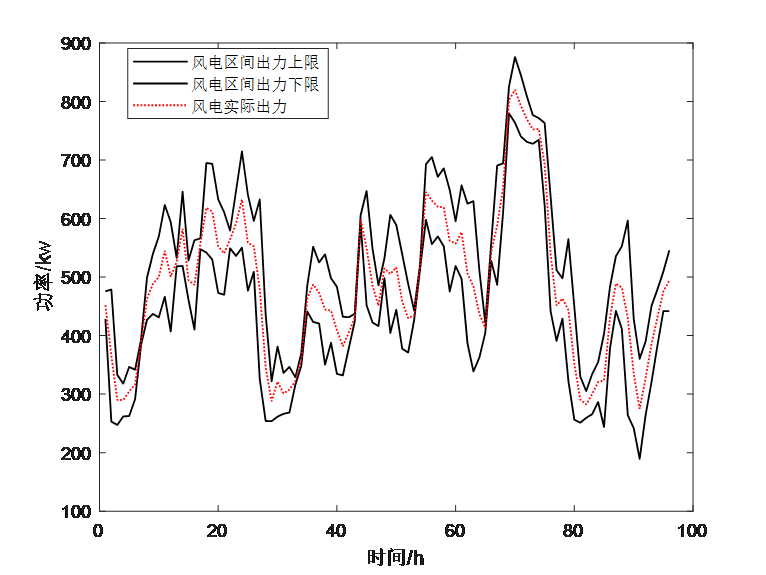
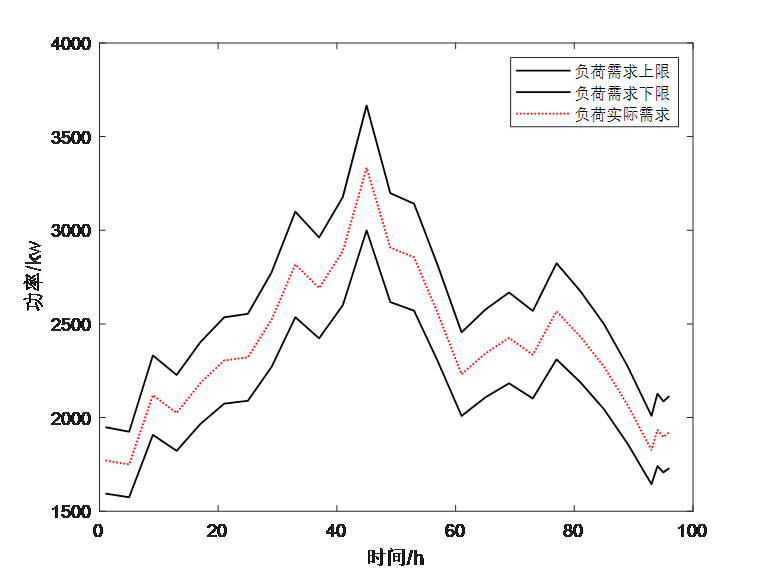
这部分是采用粒子群算法和神经网络对风电和光伏的输出功率进行预测,该部分内容和实现原理比较简单,而且不是文献的重点内容,这里不再过多介绍。这部分需要得到的结果就是下面两个公式和两个图。

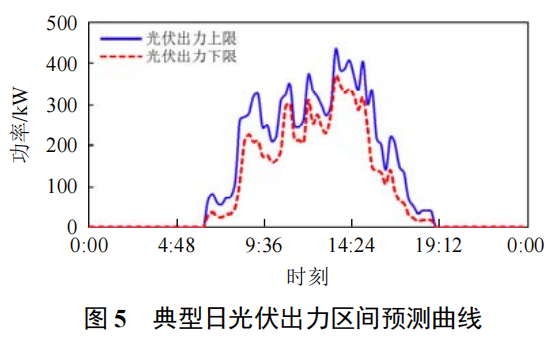
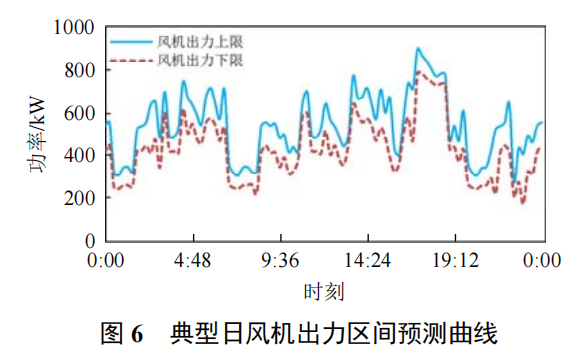
2.2 配电网鲁棒动态重构模型
配电网鲁棒重构模型中所有节点注入功率不再用某一确定的预测值模糊表示,而是均以仿射数分别予以刻画,在给定 DG 和负荷不确定范围内搜索到最恶劣波动场景下的最优网损(第一阶段)以及制定出 DG 和负荷处于最恶劣波动场景下,满足网络经济运行的重构方案(第二阶段)。为此,建立如下式所示的配电网鲁棒动态重构数学模型:
1)目标函数。


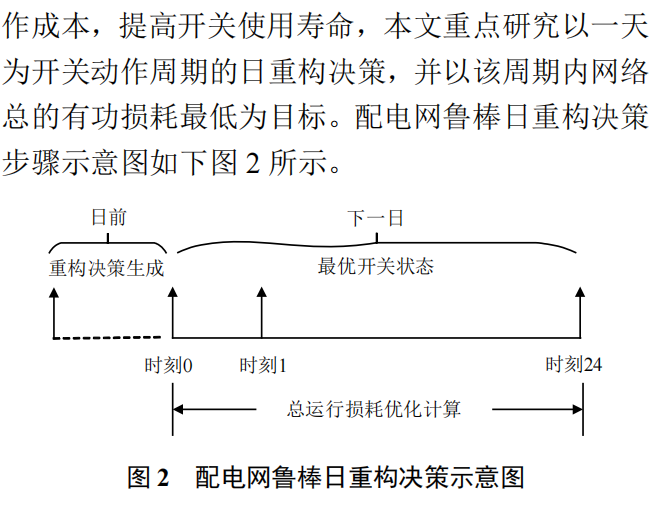

由目标函数可知,第一阶段是以负荷需求和分布式电源出力的不确定扰动为决策变量,也即基于当前网络拓扑结构计算出不确定扰动最恶劣情形下的最低网损成本;第二阶段则以支路开关状态为决策变量,也即在所有网络可能存在的拓扑结构中,寻求出能够确保重构周期内开关动作耗费与网络有功损耗等综合成本最低的唯一网络拓扑结构。显然,第二阶段目标函数也即鲁棒重构总的目标函数。
2)约束条件。



综上所述,所建立的考虑节点注入功率不确定性的配电网鲁棒动态重构数学模型以式(8)为目标函数,以式(9)—(12)为约束条件。
2.3模型求解方法
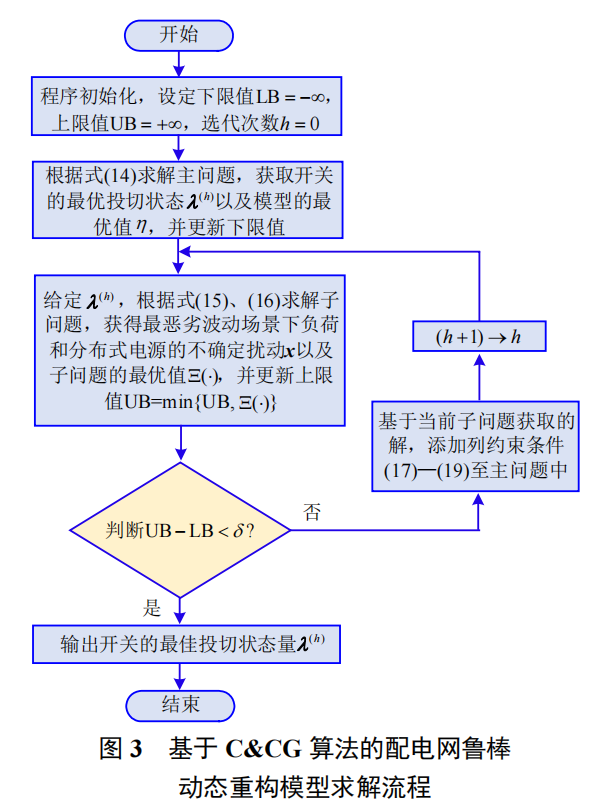
3.文献中的问题分析
3.1 分段线性逼近
如文献中所述,对于有功功率和无功功率的平方项,可采用分段线性逼近的方法进行处理。由该方法的原理可知,如果分段数太少,线性化后的结果误差会很大,如果分段数太多,又会增加很多额外的变量,加大求解难度。原文3.3.1小节中设分段数为265段,由此增加了265×2×75×96≈384万个变量,模型求解将非常困难,如果设备不是非常好的话建议还是不要参考该方法(我用自己的垃圾电脑大概尝试过,Yalmip+gurobi跑一整天也才收敛到90%,要求收敛精度1%以内的话估计得跑好几个月,文中算例分析上写的只需要400多秒,不知道是怎么得到的)。这个文献对目标函数进行线性化其实就是为了可以将两阶段鲁棒优化子问题转为对偶问题。但实际上,没有线性化之前的子问题是一个二次规划问题,可以采用KKT条件进行转换,得到的结果更精确,也不需要线性化。
3.2 数学模型的细节问题
1)对于功率平衡方程(12),没有解释变量的的含义,根据分析可知该变量应为主电源节点的输出功率。
2)该文章标题是动态重构,但实际上设置的开关状态变量并未考虑时序性,也就是在长时间内都会保持一种运行方案,其实也就是静态重构,不知道他这个动态重构体现在哪里。
3)目标函数中,支路有功功率和无功功率使用的都是分段后的变量,但是其余约束中支路功率又都用了分段前的变量,上下文没有统一,且没有给出两者之间的关系。
4)不确定变量没有给定波动的范围(也就是96个时段中最多有多少个数据点可以取得波动上限),那么最恶劣场景一定是所有DG出力取最小值,所有负荷需求取最大值,鲁棒优化结果过于保守。所以我在代码中加入了不确定预算,避免两阶段鲁棒优化的结果过于保守。新增约束公式如下:
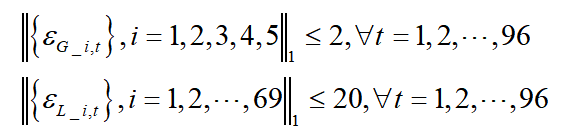
3.3 部分参数没有提供
1)文中并没有提供一天之内的负荷预测值,因此代码是找了一个典型日负荷曲线带入。
2)文中没有提供支路的最大有功和无功功率,代码里是参考其他文献设置的功率上限。
3)文中没有提供新增联络线的电阻和电抗,代码中是参考其他文献进行设置。
4)文中并未提供动态重构时最大的动作次数,代码将其设置为8次。
3.4 算例分析结果的问题
原文献中表1的结果显示,确定性重构时一天内总有功损耗为481.844kWh,总成本为302.623元,但是式(7)后的解释将C1设置为0.2,C2设置为0.8,0.8×481.844,得到的结果和302.623完全不同,不知道这个结果是怎么得到的。
4.编程思路
4.1参数和变量定义
表1 相关参数
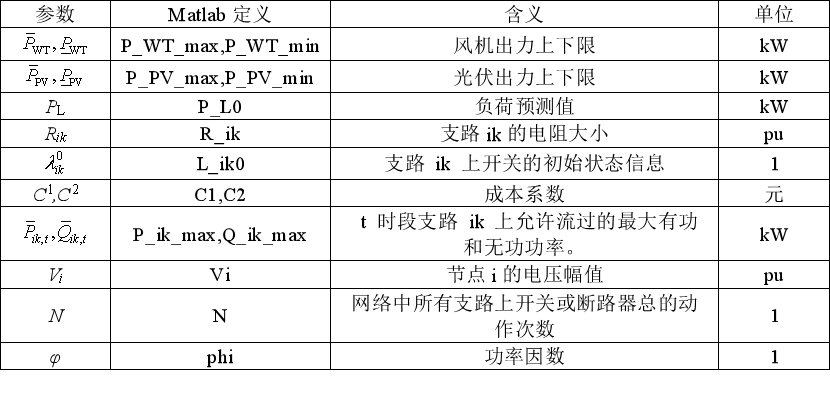
表2 决策变量

4.2编程思路
根据对文献内容的解读,可以设计下面的编程思路:
步骤1:输入所需数据
这一步比较简单。PG&E 69节点系统参数来源于matpower工具箱,部分未提供的参数需要自己假设,然后将所有需要的数据,按照表1的定义格式输入即可。需要注意的是,matpower中69节点系统编号和原文中不完全一致,为了编程更方便,代码中以matpower工具箱所提供的编号方式为准,新的编号见下图(其中红色虚线为文中新增的联络线):
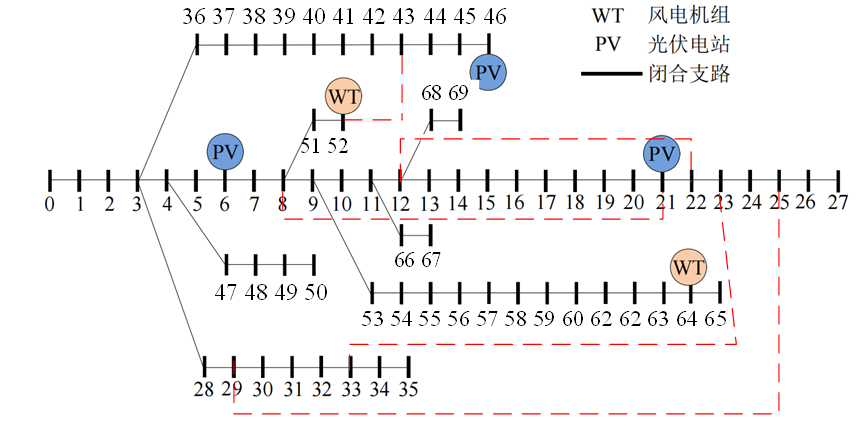
步骤2:建立确定性优化模型并求解
文中将两阶段鲁棒动态重构模型和确定性动态重构的结果进行对比,因此复现时还需要先求出确定性动态重构的结果,具体结果如下:

步骤3:建立两阶段鲁棒优化模型并求解
可以参考我之前写的博客对该问题的两阶段鲁棒优化形式进行分析(鲁棒优化入门(6)-CSDN博客和鲁棒优化入门(7)-CSDN博客)。标准的两阶段鲁棒优化问题的形式为:
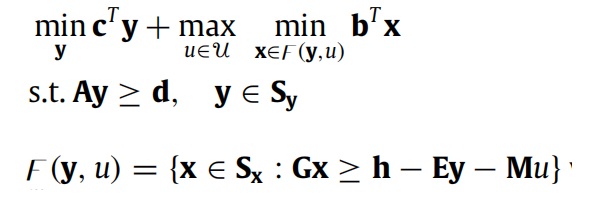



可以采用Yalmip工具箱中的函数depends、getbase、getbasematrix、see写出约束矩阵取值,具体如何操作可以参考我之前的博客(Yalmip使用教程(6)-将约束条件写成矩阵形式-CSDN博客)。



4.部分Matlab代码
程序共有4个m文件和一个mat文件,其中case69.m是69节点系统的数据文件,main_do.m是确定性优化的主程序,运行这个代码即可得到确定性优化结果;main_ro.m是两阶段鲁棒优化的主程序,运行即可得到两阶段鲁棒动态重构的结果;Matrix.m是求系数矩阵的程序,运行即可得到系数矩阵的求解结果,并将结果存在Matrix.mat文件中方便读取,其中main_do.m的部分代码如下所示:
%% 1.确定性动态重构%% 清除内存空间
clc
clear
close all
warning off%% 系统参数
mpc = case69;
nb = length(mpc.bus(:,1)); % 节点数
ns = 1; % 主电源节点
nl = length(mpc.branch(:,1)); % 支路数目
nT = 96; % 调度时段数
Y_pv = [6,21,46]; % 光伏接入节点
Y_wt = [52 64]; % 风电接入节点
Data = xlsread('风光负荷数据.xlsx'); % 读取风光负荷数据
P_PV_max = Data(:,2)'/1000/mpc.baseMVA; % 光伏出力上限
P_PV_min = Data(:,3)'/1000/mpc.baseMVA; % 光伏出力下限
P_WT_max = Data(:,4)'/1000/mpc.baseMVA; % 风电出力上限
P_WT_min = Data(:,5)'/1000/mpc.baseMVA; % 风电出力下限
PL_curve = Data(:,6); % 负荷日变化曲线
P_PV0 = (P_PV_max + P_PV_min)/2; % 光伏出力均值
dP_PV0 = P_PV_max - P_PV0; % 光伏出力最大波动
P_WT0 = (P_WT_max + P_WT_min)/2; % 风电出力均值
dP_WT0 = P_WT_max - P_WT0; % 风电出力最大波动
phi = 0.85; % DG的功率因数
P_L0 = mpc.bus(:,3)/mpc.baseMVA*PL_curve'; % 有功负荷
Q_L0 = mpc.bus(:,4)/mpc.baseMVA*PL_curve'; % 无功负荷
P_L0(P_L0 == 0) = 1e-6; % 加上一个很小的数防止0注入节点出现
Q_L0(Q_L0 == 0) = 1e-6; % 加上一个很小的数防止0注入节点出现
R_ik = mpc.branch(:,3); % 线路电阻
L_ik0 = mpc.branch(:,11); % 初始线路开断状态
C1 = 0.2; % 支路开关动作一次所需要的成本系数
C2 = 0.8; % 网络重构期间有功损耗所对应的成本系数
P_ik_max = 6; % t时段支路 ik 上允许流过的最大有功功率
Q_ik_max = 5; % t时段支路 ik 上允许流过的最大无功功率
Vi = 1; % 根据文献式(6)后的解释将节点电压设为常数1
N = 8; % 最大重构次数
Ps_max = 10; % 上级电源输出有功功率最大值
Ps_min = 0; % 上级电源输出有功功率最小值
Qs_max = 10; % 上级电源输出无功功率最大值
Qs_min = -10; % 上级电源输出无功功率最小值
branch_to_node = zeros(nb,nl); % 流入节点的支路
branch_from_node = zeros(nb,nl); % 流出节点的支路
for k = 1:nlbranch_to_node(mpc.branch(k,2),k) = 1;branch_from_node(mpc.branch(k,1),k) = 1;
end%% 决策变量
L_ik = binvar(nl,1); % 支路 ik 上开关的状态信息
u_ik = binvar(nb,nb,'full'); % 表示节点关系Pikt = sdpvar(nl,nT); % t时刻支路ik在l断面的有功功率
Qikt = sdpvar(nl,nT); % t时刻支路ik在j断面的无功功率
Ps_it = sdpvar(ns,nT); % t时刻主电源节点i的有功出力
Qs_it = sdpvar(ns,nT); % t时刻主电源节点i的无功出力e_Git = zeros(5,nT); % t时段导致 DG 节点 i 注入功率不确定的扰动因子(包含光伏和风机),确定性优化时取值为0
e_Lit = zeros(nb,nT); % t时段导致负荷节点i注入功率不确定的扰动因子,确定性优化时取值为0%% 约束条件
Constraints = [];%% 约束(10)
此处省略。。。。%% 约束(11)
此处省略。。。。%% 约束(12)
此处省略。。。。%% 目标函数
此处省略。。。。%% 设求解器
% gurobi求解器
ops = sdpsettings('verbose', 3, 'solver', 'gurobi','showprogress',1,'debug',1);
ops.gurobi.TimeLimit = 7200; % 运行时间限制
ops.gurobi.MIPGap = 0.01; % 收敛精度限制为0.01% cplex求解器
% ops = sdpsettings('verbose', 3, 'solver', 'cplex','showprogress',1,'debug',1);
% ops.cplex.timelimit = 7200; % 运行时间限制
% ops.cplex.mip.tolerances.mipgap = 0.01; % 收敛精度限制为0.01% mosek求解器
% ops=sdpsettings('verbose', 3, 'solver', 'MOSEK','cachesolvers',1);
% ops.mosek.MSK_DPAR_OPTIMIZER_MAX_TIME = 7200; % 运行时间限制
% ops.mosek.MSK_DPAR_MIO_TOL_REL_GAP = 0.01; % 收敛精度限制为0.01sol = optimize(Constraints,objective,ops);%% 分析错误标志
if sol.problem == 0disp('求解成功');
elsedisp('运行出错');yalmiperror(sol.problem)
end%% 结果
L_ik = value(L_ik);
u_ik = value(u_ik);
% disp('******************重构前******************')
% disp('开断支路为:')
% disp([num2str(mpc.branch(70,1)),'-',num2str(mpc.branch(70,2)),',',...
% num2str(mpc.branch(71,1)),'-',num2str(mpc.branch(71,2)),',',...
% num2str(mpc.branch(72,1)),'-',num2str(mpc.branch(72,2)),',',...
% num2str(mpc.branch(73,1)),'-',num2str(mpc.branch(73,2)),',',...
% num2str(mpc.branch(74,1)),'-',num2str(mpc.branch(74,2))])
% disp(['系统网损为:','36579.1335kW'])
disp('******************确定性优化重构结果******************')
open_branch = find(L_ik~=1)';
disp('开断支路为:')
disp([num2str(mpc.branch(open_branch(1),1)),'-',num2str(mpc.branch(open_branch(1),2)),',',...num2str(mpc.branch(open_branch(2),1)),'-',num2str(mpc.branch(open_branch(2),2)),',',...num2str(mpc.branch(open_branch(3),1)),'-',num2str(mpc.branch(open_branch(3),2)),',',...num2str(mpc.branch(open_branch(4),1)),'-',num2str(mpc.branch(open_branch(4),2)),',',...num2str(mpc.branch(open_branch(5),1)),'-',num2str(mpc.branch(open_branch(5),2))])
disp(['系统网损为:',num2str(value(objective2)*1000*mpc.baseMVA),'kW'])
disp(['开关动作次数为:',num2str(value(objective1)),'次'])
disp(['总运行成本为:',num2str(value(objective)),'元'])figure
plot(P_PV_max*1000*mpc.baseMVA,'k-','linewidth',1)
hold on
plot(P_PV_min*1000*mpc.baseMVA,'k-','linewidth',1)
hold on
plot(P_PV0*1000*mpc.baseMVA,'r:','linewidth',1)
legend('光伏区间出力上限','光伏区间出力下限','光伏实际出力');
xlabel('时间')
ylabel('功率/kw')figure
plot(P_WT_max*1000*mpc.baseMVA,'k-','linewidth',1)
hold on
plot(P_WT_min*1000*mpc.baseMVA,'k-','linewidth',1)
hold on
plot(P_WT0*1000*mpc.baseMVA,'r:','linewidth',1)
legend('风电区间出力上限','风电区间出力下限','风电实际出力');
xlabel('时间')
ylabel('功率/kw')figure
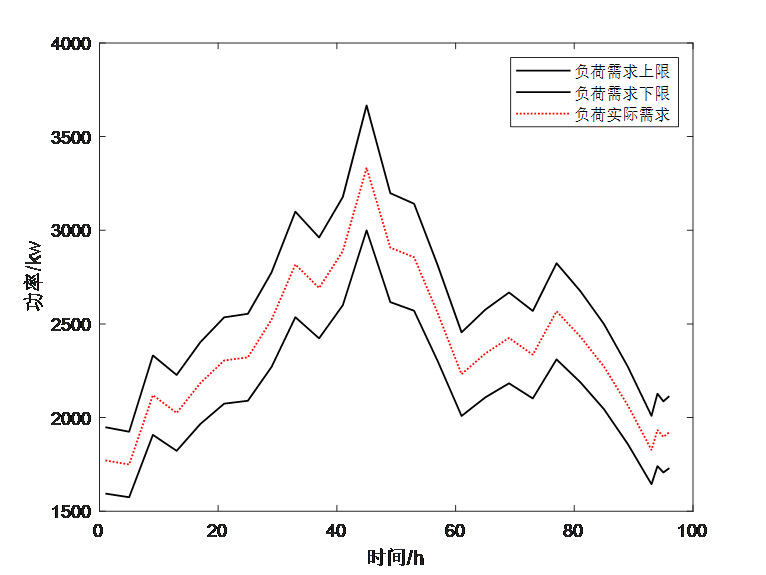
plot(1.1*sum(P_L0)*1000*mpc.baseMVA,'k-','linewidth',1)
hold on
plot(0.9*sum(P_L0)*1000*mpc.baseMVA,'k-','linewidth',1)
hold on
plot(sum(P_L0)*1000*mpc.baseMVA,'r:','linewidth',1)
legend('负荷需求上限','负荷需求下限','负荷实际需求');
xlabel('时间')
ylabel('功率/kw')经过测试,如果在main_ro.m中将代码81行的收敛精度ops.gurobi.MIPGap设置为0.05时,两阶段鲁棒优化大约需要10min即可收敛;如果将其设置为0.1时,5min左右即可收敛。大家可以根据自身需求对计算精度和运行时间的要求选择合适的收敛精度。
5.代码运行结果
原文中数据提供不全,且部分模型问题解释不清,所以代码复现结果和原文献相比会有偏差,但原理完全一样。
5.1 确定性动态重构结果

5.2 两阶段鲁棒动态重构结果

6.完整代码获取链接
(注意,代码运行需要安装Matpower以及Yalmip工具箱,以及Gurobi求解器,如果有其他求解器,可以在设置中进行更改):
考虑分布式电源不确定性的配电网鲁棒动态重构matlab代码资源-CSDN文库
相关文章:

(文章复现)考虑分布式电源不确定性的配电网鲁棒动态重构
参考文献: [1]徐俊俊,吴在军,周力,等.考虑分布式电源不确定性的配电网鲁棒动态重构[J].中国电机工程学报,2018,38(16):4715-47254976. 1.摘要 间歇性分布式电源并网使得配电网网络重构过程需要考虑更多的不确定因素。在利用仿射数对分布式电源出力的不确定性进行合…...

蓝桥杯第八届c++大学B组详解
目录 1.购物单 2.等差素数列 3.承压计算 4.方格分割 5.日期问题 6.包子凑数 7.全球变暖 8.k倍区间 1.购物单 题目解析:就是将折扣字符串转化为数字,进行相加求和。 #include<iostream> #include<string> #include<cmath> usin…...

小于n的最大数 Leetcode 902 Numbers At Most N Given Digit Set
这两个问题的本质就是一个棵树,然后根据n对树做剪枝。难点在于剪的时候边界条件有些坑,get_lower_largest_digit_dic是这两个题目的共同点 题目一: 小于n的最大数 算法题目:小于n的最大数 问题描述:给一个数组nums[5…...

Leetcode刷题-数组(二分法、双指针法、窗口滑动)
数组 1、二分法 704. 二分查找 - 力扣(LeetCode) 需要注意区间的问题。首先在最外面的循环判断条件是left<right。那就说明我们区间规定的范围就是【left,right】 属于是左闭右闭!!!!!&…...

STM32学习和实践笔记(4): 分析和理解GPIO_InitTypeDef GPIO_InitStructure (b)
继续上篇博文:STM32学习和实践笔记(4): 分析和理解GPIO_InitTypeDef GPIO_InitStructure (a)-CSDN博客 往下写, 为什么:当GPIO_InitStructure.GPIO_PinGPIO_Pin_0 ; 时,其实就是将对应的该引脚的寄存器地…...

数据仓库——事实表
数据仓库基础笔记思维导图已经整理完毕,完整连接为: 数据仓库基础知识笔记思维导图 事实表 事务事实表 事务事实表用于跟踪事件,通过存储事实和与之关联的维度细节,允许单独或聚集地研究行为。粒度稀疏性包含可加事实 无事实的…...

人工智能常用的编程语言有哪些?
人工智能常用的编程语言包括Python、Java、C、R、Lisp和Prolog等。具体选择取决于项目需求、技术背景和性能要求。 Python是AI领域的明星语言,由于其简洁易懂的语法、丰富的库支持以及庞大的社区资源,适用于机器学习、深度学习和自然语言处理等领域。 …...

【Leetcode每日一题】模拟 - 提莫攻击(难度⭐)(45)
1. 题目解析 题目链接:495. 提莫攻击 2.算法原理 一、分情况讨论 要计算中毒的总时长,我们需要考虑时间点之间的差值,并根据这些差值来确定中毒的实际持续时间。 情况一:差值大于等于中毒时间 假设你的角色在时间点A中毒&#…...
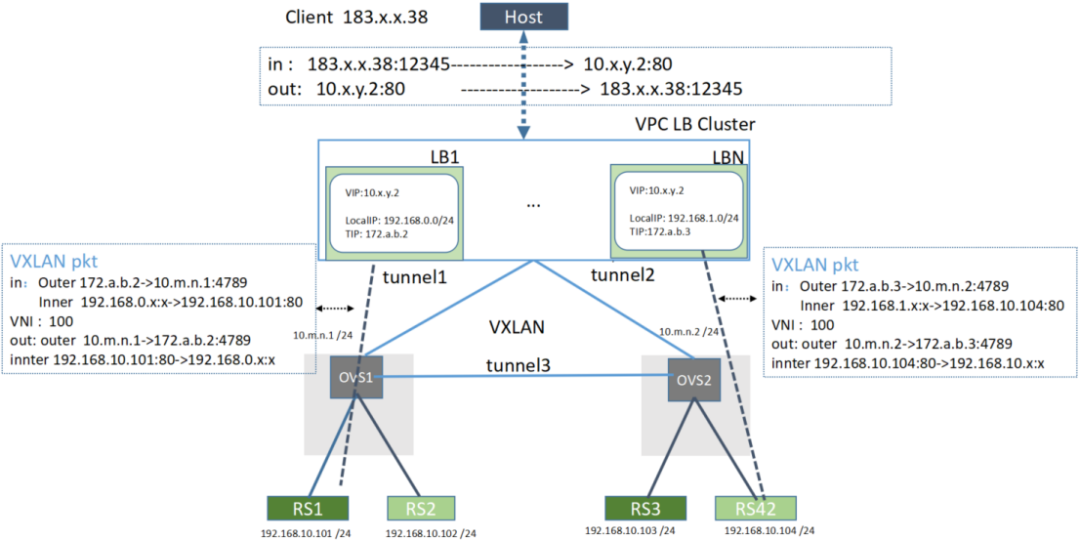
OPPO云VPC网络实践
1 OPPO 云网络现状 随着OPPO业务的快速发展,OPPO云规模增长迅速。大规模虚拟实例的弹性伸缩、低延时需求对网络提出了诸多挑战。原有基于VLAN搭建的私有网络无法解决这些问题,给网络运维和业务的快速上线带来了挑战。 梳理存在的主要问题如下…...
找到所有数组中消失的数字)
力扣(数组)找到所有数组中消失的数字
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。 示例 1: 输入:nums [4,3,2,7,8,2,3,1] 输出:[5,6]示例 2&am…...
每日面经分享(Spring Boot: part3 Service层)
SpringBoot Service层的作用 a. 封装业务逻辑:Service层负责封装应用程序的业务逻辑。Service层是控制器(Controller)和数据访问对象(DAO)之间的中间层,负责处理业务规则和业务流程。通过将业务逻辑封装在S…...

k8s的pod访问service的方式
背景 在k8s中容器访问某个service服务时有两种方式,一种是把每个要访问的service的ip注入到客户端pod的环境变量中,另一种是客户端pod先通过DNS服务器查找对应service的ip地址,然后在通过这个service ip地址访问对应的service服务 pod客户端…...

shell脚本发布docker-nginx vue2 项目示例
docker、git、node.js安装略过。 使git pull或者git push不需要输入密码操作方法 nginx安装在docker容器里面,参见:https://blog.csdn.net/HSJ0170/article/details/128631155 姊妹篇(宿主机nginx,非docker-nginx)&am…...
【THM】Nmap Basic Port Scans(基本端口扫描)-初级渗透测试
介绍 本房间是Nmap系列的第二个房间(网络安全简介模块的一部分)。 1.Nmap实时主机发现 2.Nmap基本端口扫描 3.Nmap高级端口扫描 4.Nmap后端口扫描 在之前的房间里,我们专注于发现在线系统。到目前为止,我们已经介绍了Nmap扫描的三个步骤: 枚举目标发现活动主机反向-…...

Groovy结合Java在生产中的落地实战
Groovy简介 Groovy是用于Java虚拟机的一种敏捷的动态语言,是一种成熟的面向对象编程语言,又是一种纯粹的脚本语言。Groovy运行在JVM环境上,在语法上兼具java 语言和脚本语言特点,大大简化了语法。同时又具有闭包和动态语言中的其…...

达梦数据库 创建外部表 [-7082]:外部表数据错误.
1:定义 外部表,是指不存在于数据库中的表。通过向达梦提供描述外部表的元数据,可以把一 个操作系统文件当成一个只读的数据库表,就像这些数据存储在一个普通数据库表中一样来 进行访问。 外部表的数据存储在操作系统中࿰…...
XUbuntu22.04之激活Linux最新Typora版本(二百二十五)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...

JavaScript简介
目录 概要: 说明: 学习JS的原因: JS可以干什么: 了解JavaScript: 前言: JavaScript的历史: JavaScript与ECMAScript: 如何运行JavaScript以及JavaScrip的特点: …...

使用PaddleX实现的智慧农业病虫检测项目
目录 1. 数据集解压 2.检查数据集的图片是否均可读取 3. 查看数据集的类别信息...
算法学习——LeetCode力扣图论篇1(797. 所有可能的路径、200. 岛屿数量、695. 岛屿的最大面积)
算法学习——LeetCode力扣图论篇1 797. 所有可能的路径 797. 所有可能的路径 - 力扣(LeetCode) 描述 给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
