牛客练习赛123(A,B,C,D)
牛客挑战赛,练习赛和小白月赛周赛不是一种东西。这玩意跟CF的div12差不多难度。而且找不到题解。所以决定不等题解补题了,直接写题解了。
比赛链接
光速签到下班,rk++。感觉E可能能补掉,看情况补吧。
B题感觉之前考了两次,结论和证明构造过程需要理解,赛时记得结论直接秒了。C题是不太裸的裸完全背包,思路不裸但是写法裸。D题需要加个优化,思路看的别人的,很妙。
A 炸鸡块哥哥的粉丝题
思路:
签到,截取前一半的子串即可。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;int n;
string s;int main(){cin>>n>>s;cout<<s.substr(0,(n+1)/2);return 0;
}
B 智乃想考一道鸽巢原理
思路:
看了评论区题解才发现,自己这么长时间理解的方法原来就是鸽巢原理。指路
我们想让某一种小球留下来,肯定先让其他小球先配对抵消掉,其他小球抵消剩下的再用这种小球来消。那么问题就变成了求其他小球抵消剩下的小球有几个,如果剩下的球比这种小球少,那就可以剩下这种小球,否则就剩不下。
我们把最多的那个小球看作是鸽巢,然后剩余的小球看作是鸽子,也就是鸽巢有 m x mx mx 个,鸽子有 r m = t o t − a i rm=tot-a_i rm=tot−ai 个。
- 当 m x > ⌊ r m 2 ⌋ mx\gt \left\lfloor\dfrac{rm}2\right\rfloor mx>⌊2rm⌋ 时:可以每个鸽巢放入一只鸽子,此时剩余的小球个数就是剩余的鸽巢个数,即 m x − ( r m − m x ) = 2 ∗ m x − r m mx-(rm-mx)=2*mx-rm mx−(rm−mx)=2∗mx−rm。
- 当 m x ≤ ⌊ r m 2 ⌋ mx\le \left\lfloor\dfrac{rm}2\right\rfloor mx≤⌊2rm⌋ 时:可以用其他小球来充当鸽巢,使得鸽巢拓展到 ⌈ r m 2 ⌉ \left\lceil\dfrac{rm}2\right\rceil ⌈2rm⌉ 个。然后其他小球依次放入鸽巢即可,可以保证存在一种方法使得小球不会放在同种颜色小球的鸽巢里(因为最少可以只有一种颜色又当鸽巢又放小球,其他颜色就不可能重复了。而每种颜色小球个数不会超过 ⌈ r m 2 ⌉ \left\lceil\dfrac{rm}2\right\rceil ⌈2rm⌉ 个,所以这种颜色可以不重复)。此时会剩余 r m % 2 rm\%2 rm%2 个鸽巢。
所以我们枚举 i i i 时,对每个 i i i 只要知道剩余的小球的总个数和剩余最大个数的小球,就可以计算其他小球抵消最后会剩多少小球,也就知道能否剩下这种小球。我们可以设置一个变量记录所有小球个总个数,并处理出前缀最大值和后缀最大值,这样就可以快速查询了。
code:
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const int maxn=1e6+5;int T,n;
int a[maxn],prem[maxn],sufm[maxn];
ll tot;int main(){cin>>T;while(T--){cin>>n;tot=0;for(int i=1;i<=n+1;i++)prem[i]=sufm[i]=0;for(int i=1;i<=n;i++){cin>>a[i];prem[i]=max(prem[i-1],a[i]);tot+=a[i];}for(int i=n;i>=1;i--)sufm[i]=max(sufm[i+1],a[i]);for(int i=1;i<=n;i++){ll mx=max(prem[i-1],sufm[i+1]),rm=tot-a[i],lst;if(mx>rm/2)lst=2*mx-rm;else lst=rm&1;cout<<"01"[a[i]>lst]<<" \n"[i==n];}}return 0;
}
C 智乃想考一道完全背包(Easy version)
思路:
如果位置 k k k 上的物品本来就很好了,那么肯定选这个物品就行了。但是如果有个很好的物品远离位置 k k k,那么我们就需要选上从这个位置到 k k k 上的所有物品,才能选上这一个物品,它就相当于和中间的物品进行捆绑销售了。
反正一定会捆绑销售,所以我们不如一开始就将 l ∼ k l\sim k l∼k 或 k ∼ r k\sim r k∼r 位置上的物品进行绑定,把它们变成一个物品,然后跑完全背包。
不过由于我们选了 l ∼ k l\sim k l∼k 的物品的话,我们还能去拓展另一边到 r r r,并省下一个 k k k。所以另一边我们也需要绑定过来,也就是说需要把 l ∼ r l\sim r l∼r 上的物品进行绑定。
如果我们以位置为横坐标,每个位置上物品选择的个数为纵坐标画直方图的话,它的形状就是一个金字塔型。我们绑定物品同时选取,其实就相当于绑定一行,每行都是整块选取。
时间复杂度看似是 O ( n 2 ∗ m ) O(n^2*m) O(n2∗m) 的。但是由于背包容量最多 m m m,重量超过 m m m 的物品我们根本更新不了答案,所以最多有 m 2 m^2 m2 级别个物品会更新 d p dp dp 值,所以时间复杂度最多是 O ( n 2 + m 3 ) O(n^2+m^3) O(n2+m3) 的。
code:
没必要开longlong
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=2005;
const int maxm=505;
typedef long long ll;
const ll linf=1e18;int n,m,k;
ll dp[maxm];ll tw[maxn],tv[maxn];int main(){cin>>n>>m>>k;for(int i=1;i<=n;i++){cin>>tw[i]>>tv[i];tw[i]+=tw[i-1];tv[i]+=tv[i-1];}for(int l=1;l<=k;l++)for(int r=k;r<=n;r++){ll w=tw[r]-tw[l-1],v=tv[r]-tv[l-1];for(int j=w;j<=m;j++)dp[j]=max(dp[j],dp[j-w]+v);}for(int i=1;i<=m;i++){dp[i]=max(dp[i-1],dp[i]);cout<<dp[i]<<" ";}return 0;
}
D 智乃想考一道完全背包(Hard version)
思路:
朴素的想法是设 d p [ k ] [ j ] dp[k][j] dp[k][j] 表示位置 k k k 为中心,容量为 j j j 的最大价值。直接枚举 k k k 的位置,对每个位置做法和上面相同,这样时间复杂度就会变成 O ( n ∗ m 3 ) O(n*m^3) O(n∗m3),会 T T T 掉 1 3 \frac13 31 的点。
考虑优化,发现对于选取了区间 l ∼ r l\sim r l∼r 的整块物品,它可以去更新 k ∈ [ l , r ] k\in[l,r] k∈[l,r] 的所有位置,而没有必要在选取不同 k k k 的时候分别去更新每个 d p [ k ] [ − ] dp[k][-] dp[k][−]。
原本我们先从小到大枚举 l l l,固定好 l l l 后,然后枚举 r r r 和 k k k,对一个位置 k k k,它应该用 [ l , r = k ∼ n ] [l,r=k\sim n] [l,r=k∼n] 的物品来更新。这里为了实现上面说的优化,我们从大到小枚举 r r r,并且令 k = r k=r k=r,这样算出来的 d p [ r ] [ − ] dp[r][-] dp[r][−] 就考虑到了 [ l , r = k ∼ n ] [l,r=k\sim n] [l,r=k∼n] 所有物品。 d p [ r ] [ − ] dp[r][-] dp[r][−] 直接从 d p [ r + 1 ] [ − ] dp[r+1][-] dp[r+1][−] 转移过来或者从 [ l , r ] [l,r] [l,r] 这件物品转移过来即可
这样优化后,由于不需要枚举 k k k 的位置,时间复杂度被优化成了 O ( m 3 ) O(m^3) O(m3)。可以通过。
code:
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=2005;
const int maxm=505;
typedef long long ll;
const ll linf=1e18;int n,m;
ll dp[maxn][maxm];
//位置为k,背包容量为j ll tw[maxn],tv[maxn];
int ans[maxn],id[maxn];int main(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>tw[i]>>tv[i];tw[i]+=tw[i-1];tv[i]+=tv[i-1];}for(int l=1;l<=n;l++){ll w,v;for(int r=n;r>=l;r--){w=tw[r]-tw[l-1];v=tv[r]-tv[l-1];for(int j=w;j<=m;j++)dp[r][j]=max(dp[r][j],max(dp[r+1][j],dp[r][j-w]+v));}}for(int i=1;i<=m;i++){ll maxx=-linf,idx;for(int k=1;k<=n;k++){dp[k][i]=max(dp[k][i-1],dp[k][i]);if(dp[k][i]>maxx){maxx=dp[k][i];idx=k;}}ans[i]=maxx;id[i]=idx;}for(int i=1;i<=m;i++)cout<<ans[i]<<" \n"[i==m];for(int i=1;i<=m;i++)cout<<id[i]<<" \n"[i==m];return 0;
}
相关文章:
)
牛客练习赛123(A,B,C,D)
牛客挑战赛,练习赛和小白月赛周赛不是一种东西。这玩意跟CF的div12差不多难度。而且找不到题解。所以决定不等题解补题了,直接写题解了。 比赛链接 光速签到下班,rk。感觉E可能能补掉,看情况补吧。 B题感觉之前考了两次&#x…...
docker部署-RabbitMq
1. 参考 RabbitMq官网 docker官网 2. 拉取镜像 这里改为自己需要的版本即可,下面容器也需要同理修改 docker pull rabbitmq:3.12-management3. 运行容器 docker run \ --namemy-rabbitmq-01 \ -p 5672:5672 \ -p 15672:15672 \ -d \ --restart always \ -…...
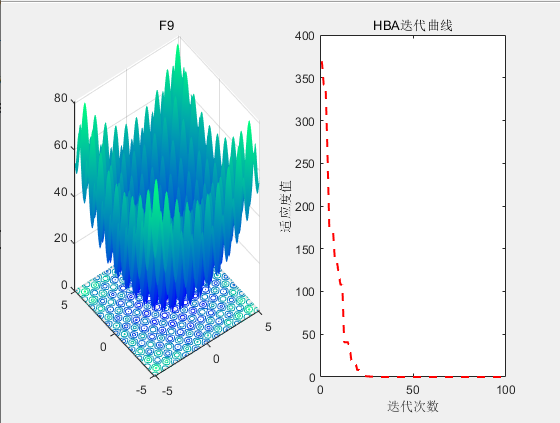
【智能算法】蜜獾算法(HBA)原理及实现
目录 1.背景2.算法原理2.1算法思想2.2算法过程 3.结果展示4.参考文献 1.背景 2021年,FA Hashim等人受到自然界中蜜獾狩猎行为启发,提出了蜜獾算法((Honey Badger Algorithm,HBA)。 2.算法原理 2.1算法思想 蜜獾以其…...
9、鸿蒙学习-开发及引用静态共享包(API 9)
HAR(Harmony Archive)是静态共享包,可以包含代码、C库、资源和配置文件。通过HAR可以实现多个模块或多个工程共享ArkUI组件、资源等相关代码。HAR不同于HAP,不能独立安装运行在设备上,只能作为应用模块的依赖项被引用。…...

[Pytorch]:PyTorch中张量乘法大全
在 PyTorch 中,有多种方法可以执行张量之间的乘法。这里列出了一些常见的乘法操作: 总结: 逐元素乘法:*ortorch.mul()矩阵乘法:ortorch.mm()ortorch.matmul()点积:torch.Tensor.dot()批量矩阵乘法ÿ…...

【软考】防火墙技术
目录 1. 概念2. 包过滤防火墙3. 应用代理网关防火墙4. 状态检测技术防火墙 1. 概念 1.防火墙(Firewall)是建立在内外网络边界上的过滤封锁机制,它认为内部网络是安全和可信赖的,而外部网络是不安全和不可信赖的。2.防火墙的作用是防止不希望的、未经授权…...

OpenHarmony实战:Makefile方式组织编译的库移植
以yxml库为例,其移植过程如下文所示。 源码获取 从仓库获取yxml源码,其目录结构如下表: 表1 源码目录结构 名称描述yxml/bench/benchmark相关代码yxml/test/测试输入输出文件,及测试脚本yxml/Makefile编译组织文件yxml/.gitat…...

嵌入式C语言--GPT通用定时器
嵌入式C语言–GPT通用定时器 嵌入式C语言--GPT通用定时器 嵌入式C语言--GPT通用定时器一. GPT基本概念二. GPT的作用三. GPT通道的四个状态四. Continuous/One-Shot模式3.1)Continuous模式3.2)One-Shot模式 一. GPT基本概念 GPT即General Purpose Timer…...

『Apisix系列』破局传统架构:探索新一代微服务体系下的API管理新范式与最佳实践
一、『Apisix安装部署』 🚀 1.1 手把手教你从零部署APISIX高性能API网关 二、『Apisix入门篇』 🚀 2.1 从零到一掌握Apache APISIX:架构解析与实战指南 三、『Apisix进阶篇』 🚀 3.1 动态负载均衡:APISIX的实战演练…...
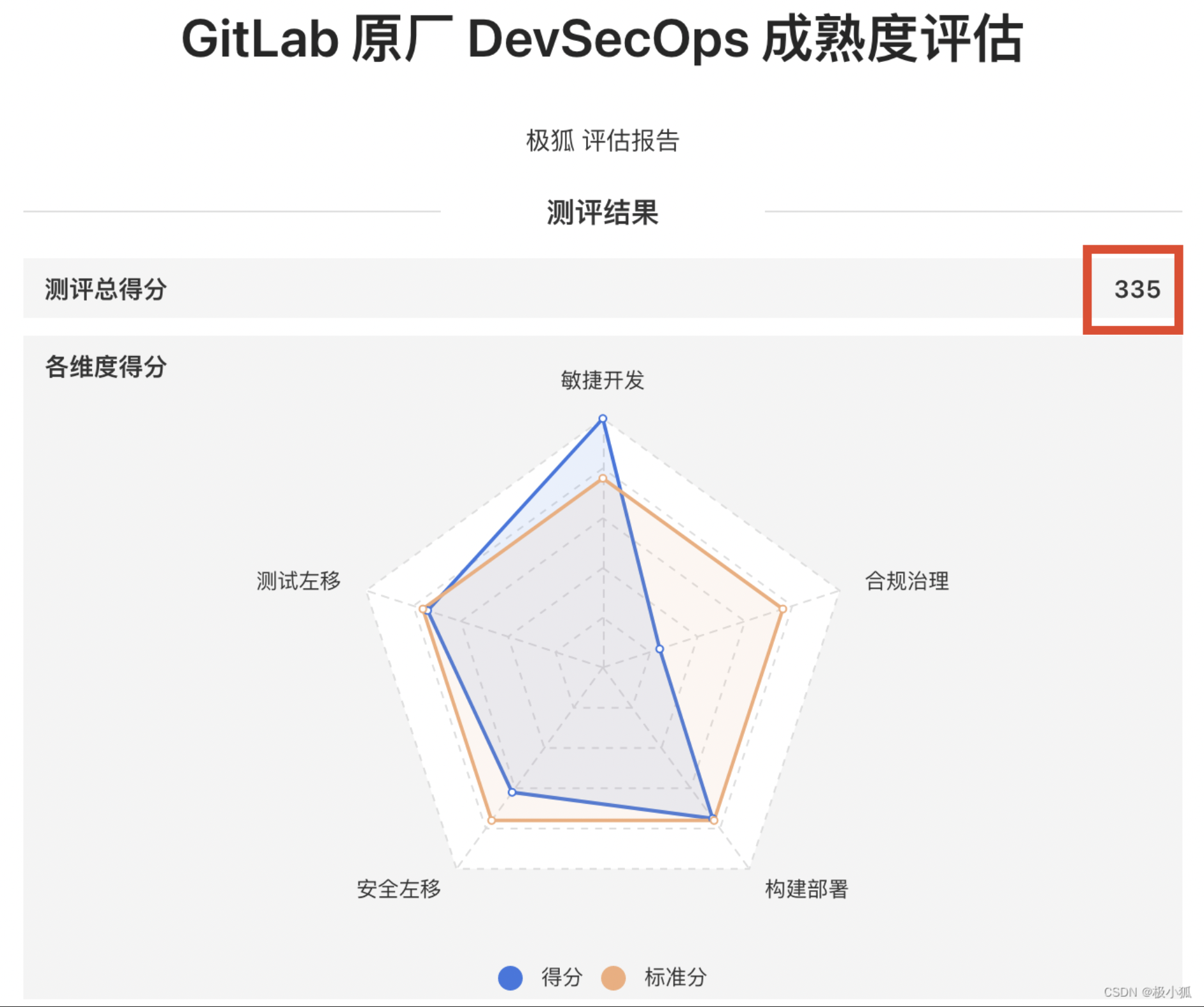
如何在极狐GitLab 自定义 Pages 域名、SSL/TLS 证书
本文作者:徐晓伟 GitLab 是一个全球知名的一体化 DevOps 平台,很多人都通过私有化部署 GitLab 来进行源代码托管。极狐GitLab 是 GitLab 在中国的发行版,专门为中国程序员服务。可以一键式部署极狐GitLab。 本文主要讲述了在极狐GitLab 用户…...

React Native 应用打包
引言 在将React Native应用上架至App Store时,除了通常的上架流程外,还需考虑一些额外的优化策略。本文将介绍如何通过配置App Transport Security、Release Scheme和启动屏优化技巧来提升React Native应用的上架质量和用户体验。 配置 App Transport…...

单链表就地逆置
算法思想:构建一个带头结点的单链表L,然后访问链表中的每一个数据结点,将访问到的数据结点依此插入到L的头节点之后。 #define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> typedef int ElemType; typedef s…...
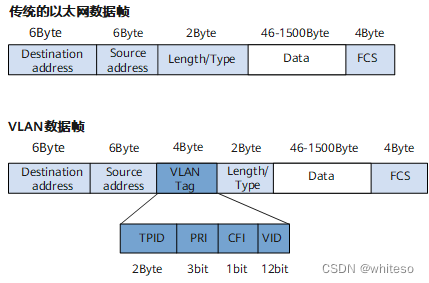
MTU/TCPMSS/VLAN/ACCESS/TRUNK/HYBRID
MTU RFC标准定义以太网的默认MTU值为1500 最小64字节是为了保证最极端的冲突能被检测到,64字节是能被检测到的最小值;最大不超过1518字节是为了防止过长的帧传输时间过长而占用共享链路太长时间导致其他业务阻塞。所以规定以太网帧大小为64~1518字节&am…...

Spring Boot的基础知识和应用
在快速发展的软件开发领域,Spring Boot已经成为了一个广受欢迎的框架,它极大地简化了Spring应用的初始搭建以及开发过程。Spring Boot遵循“约定优于配置”的原则,通过默认配置减少了开发者的配置工作量,使得开发者能够更专注于业…...

【Linux】详解动静态库的制作和使用动静态库在系统中的配置步骤
一、库的作用 1、提高开发效率,让开发者所有的函数实现不用从零开始。 2、隐藏源代码。 库其实就是所有的.o文件用特定的方式进行打包形成一个文件,各个.o文件包含了源代码中的机器语言指令。 二、动态库和静态库的制作和使用 2.1、静态库的制作和使用…...
)
开源模型应用落地-qwen1.5-7b-chat-LoRA微调(二)
一、前言 预训练模型提供的是通用能力,对于某些特定领域的问题可能不够擅长,通过微调可以让模型更适应这些特定领域的需求,让它更擅长解决具体的问题。 本篇是开源模型应用落地-qwen-7b-chat-LoRA微调(一)进阶篇,学习通义千问最新1.5系列模型的微调方式。 二、术语介绍 …...

【现代企业管理】企业组织结构和组织文化的理论与实践——以华为为例
一、前言 管理是科学和艺术的统一体,它是企业成长的保证。企业管理中,管理者面对的往往不是一个完整的系统,而是各种不具有整体规律性的零碎信息的总和,因此进行信息的整合和研究是管理的重点和关键。 组织管理作为管理的四大职…...

【Kotlin】Sequence简介
1 前言 序列(Sequence)是 Kotlin 中为方便操作集合及其元素而定制的接口,是一个延迟获取数据的集合,只有需要元素时才会生产元素。在处理大量数据时,序列可以显著地提升性能。 Sequence 类似 Java 中的 Stream…...

【Java】Thread详解
🍒前言 本文将从以下几方面来展开对Thread的介绍。 1.线程创建 2.线程中断 3.线程等待 4.线程休眠 在前面的文章中,已经总结了关于Thread的一些理解。 在阅读本文之前,最好对其有一些基础的了解。 文章链接: 【JavaSE】进程是什么?…...

QT TCP和UDP网络编程
代表网络概念的QTcpSocket,QTcpServer和QUdpSocket,以及QNetworkRequest,QNetworkReply和QNetworkAccessManager之类的高级类来执行使用通用协议的网络操作。 它还提供了QNetworkConfiguration,QNetworkConfigurationManager和QNetworkSession等,实现承载…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
