动态规划详解(Dynamic Programming)
目录
- 引入
- 什么是动态规划?
- 动态规划的特点
- 解题办法
- 解题套路框架
- 举例说明
- 斐波那契数列
- 题目描述
- 解题思路
- 方式一:暴力求解
- 思考
- 方式二:带备忘录的递归解法
- 方式三:动态规划
- 推荐练手题目
引入
动态规划问题(Dynamic Programming)应该是很多人头疼的一类问题,
本文尝试探索一种套路帮助解决此类问题
什么是动态规划?
动态规划的核心思想是将问题分解为一系列子问题,并通过记忆化或递推的方式求解子问题,从而得到原始问题的解。
动态规划的特点
其主要特点包括:
- 重叠子问题:问题的解能够通过多次重复计算相同的子问题得到。
- 最优子结构:问题的最优解能够由子问题的最优解推导得出。
解题办法
动态规划通常分为自顶向下的记忆化搜索和自底向上的递推两种方法。
解题套路框架
解决动态规划问题通常遵循以下套路框架:
递归的暴力解法 -> 带备忘录的递归解法 -> 非递归的动态规划解法。这个过程是层层递进的解决问题的过程,
具体的过程
-
确定状态
需要明确问题的状态是什么,以及在状态转移过程中如何更新状态。 -
定义状态转移方程
状态转移方程描述了状态之间的转移关系。它明确了如何从已知的状态计算出未知状态的值。 -
处理边界条件
边界条件是指状态转移的起点或终点,通常需要单独考虑和处理。 -
计算动态规划数组
使用循环遍历计算动态规划数组中的每个元素,根据状态转移方程填充数组。 -
返回结果
根据问题的具体要求,从动态规划数组中选取相应的值作为最终的结果。
举例说明
以下是一个使用动态规划解决斐波那契数列问题的示例:
斐波那契数列
题目描述
斐波那契数列是一个非常经典的数列,它的第一个和第二个数分别为 0 和 1,从第三个数开始,每个数都是前两个数之和。即斐波那契数列的定义如下:F(0) = 0,
F(1) = 1,
F(n) = F(n-1) + F(n-2) (n >= 2)给定一个整数 n,编写一个函数来计算斐波那契数列中第 n 个数的值。例如:输入:n = 0,输出:0
输入:n = 1,输出:1
输入:n = 5,输出:5
输入:n = 10,输出:55
解题思路
方式一:暴力求解
以java为例
public class Fibonacci {// 暴力递归求解斐波那契数列public static long fibonacci(int n) {// base caseif (n == 0) {return 0;} else if (n == 1) {return 1;} else {// 递归计算前两个数的和return fibonacci(n - 1) + fibonacci(n - 2);}}public static void main(String[] args) {int n = 10;long result = fibonacci(n);System.out.println("The Fibonacci number at position " + n + " is: " + result);}
}说明:
fibonacci方法用于求解第n个斐波那契数,采用递归的方式。
在方法中,首先判断n的值是否为0或1(即基本情况),如果是则返回对应的斐波那契数值。
如果n值大于1,则通过递归计算前两个数的和,即fibonacci(n-1) + fibonacci(n-2)。
在main方法中,我们定义一个整型变量n表示所求的斐波那契数的位置,然后调用fibonacci方法计算结果。
最后,打印出所求位置上的斐波那契数。
思考
学校老师讲递归的时候似乎都是拿这个举例。我们也知道这样写代码虽然简洁易懂,但是十分低效,低效在哪里?假设 n = 20,请画出递归树。
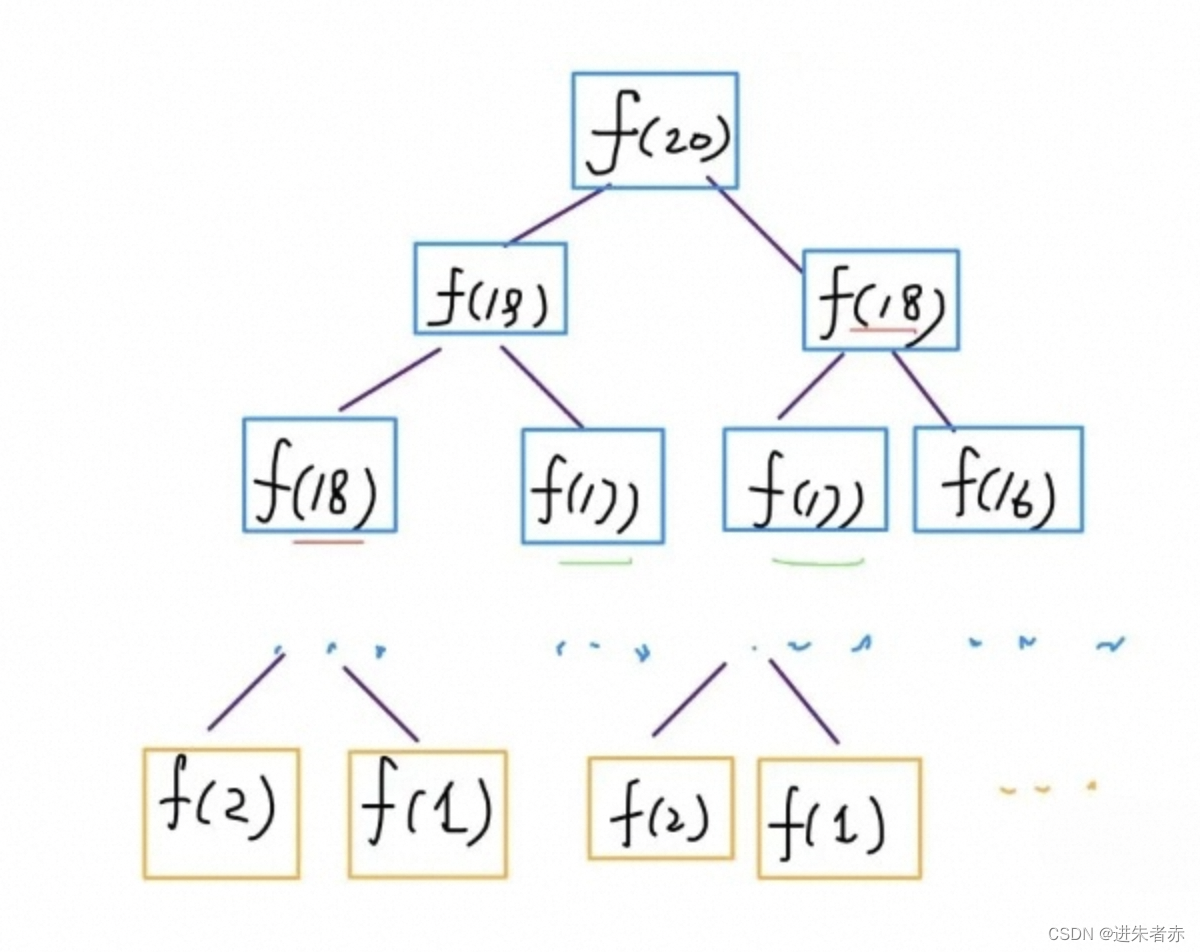
递归树是一种用于理解递归算法执行过程的图形表示方法。对于斐波那契数列问题,在递归过程中,我们可以将其表示为一棵递归树。递归树的每个节点表示一个子问题,根节点表示原问题。以计算 f(20) 为例,我们需要先计算子问题 f(19) 和 f(18),然后计算 f(19) 时又需要先计算子问题 f(18) 和 f(17),依此类推。当到达 f(1) 或 f(2) 时,可以直接返回已知的结果,递归树不再向下生长。
递归算法的时间复杂度可以通过计算子问题个数乘以解决一个子问题所需时间来得到。子问题个数指的是递归树中节点的总数。显然,在斐波那契数列的递归树中,节点总数为指数级别,即 O(2^n)。而解决一个子问题的时间,在这个算法中是常数级别的(O(1)),因为只有一个加法操作。
因此,该算法的时间复杂度为 O(2^n),是指数级别的,效率低下。
观察递归树可以明显看出算法低效的原因:存在大量的重复计算。例如,节点 f(18) 被计算了两次。而且不仅仅是节点 f(18),还有其他节点也被重复计算。因此,这个算法非常低效。
动态规划问题具备的第一个性质就是重叠子问题。接下来,我们将想办法解决这个问题。
方式二:带备忘录的递归解法
明确了重复计算是导致算法低效的主要原因后,我们可以采取一种优化策略,即使用一个「备忘录」来避免重复计算。每次计算完一个子问题的答案后,不急于返回,而是将答案存储在「备忘录」中。下次遇到同样的子问题时,先查找「备忘录」,如果已经计算过了,直接取出答案使用,避免重复计算。
通常情况下,我们可以使用数组来充当「备忘录」,但也可以使用哈希表(字典)等其他数据结构,核心思想是一样的。
java实现:
import java.util.HashMap;
import java.util.Map;public class Fibonacci {// 使用备忘录来避免重复计算private static Map<Integer, Long> memo = new HashMap<>();public static long fibonacci(int n) {// 查找备忘录,如果已经计算过,直接返回答案if (memo.containsKey(n)) {return memo.get(n);}// Base caseif (n == 0) {return 0;} else if (n == 1) {return 1;}// 计算并记录答案到备忘录中long ans = fibonacci(n - 1) + fibonacci(n - 2);memo.put(n, ans);return ans;}public static void main(String[] args) {int n = 20;long result = fibonacci(n);System.out.println("The Fibonacci number at position " + n + " is: " + result);}
}说明:
我们使用一个哈希表(字典)memo作为「备忘录」,用于存储子问题的答案。在fibonacci方法中,首先查找「备忘录」,如果已经计算过子问题n的答案,则直接返回答案。这样就避免了重复计算。
接下来,处理基本情况,即斐波那契数列的前两个数。
然后,通过递归计算并记录答案到「备忘录」中,即计算fibonacci(n-1) + fibonacci(n-2)并将结果存入memo。 最后,返回计算结果。
现在,画出递归树,你就知道「备忘录」到底做了什么。
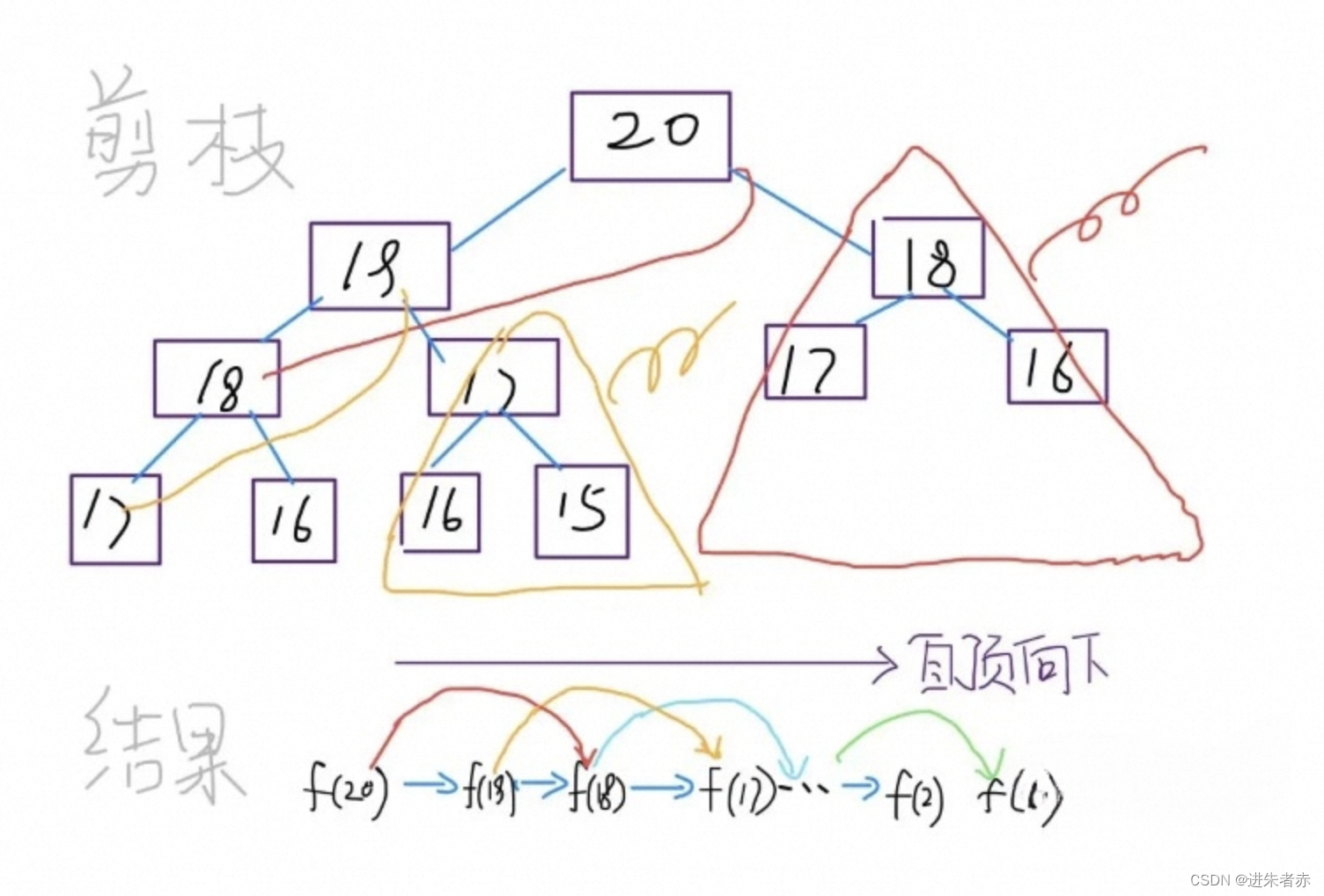
使用带有备忘录的递归算法时,我们可以将其思路分为以下几个层次进行说明:
-
第一层次:理解问题存在重复计算导致低效
我们首先明确问题的低效之处在于重复计算。观察递归树,我们发现存在大量的重复计算,例如节点 f(18) 被计算了两次,这样会浪费大量的时间。 -
第二层次:引入「备忘录」概念
为了避免重复计算,我们引入了「备忘录」的概念。在计算完一个子问题的答案后,我们将其结果存储在「备忘录」中。下次遇到相同的子问题时,先查找「备忘录」,如果已经计算过,直接返回结果,从而避免重复计算。 -
第三层次:优化时间复杂度
递归算法的时间复杂度可以通过计算子问题个数乘以解决一个子问题所需的时间来得到。对于带有备忘录的递归算法,子问题个数是与输入规模成正比的,因为我们使用备忘录避免了重复计算。解决一个子问题的时间仍然是常数级别。因此,该算法的时间复杂度为 O(n),相比于暴力算法有了显著的降低。 -
第四层次:对比「自顶向下」和「自底向上」
我们进一步将带有备忘录的递归解法与动态规划进行对比。带有备忘录的递归解法采用了「自顶向下」的思路,通过递归树从顶部向下延伸,逐步分解规模,直到达到基础情况并逐层返回答案。而动态规划采用了「自底向上」的思路,从最底部、最简单、规模最小的问题开始向上推导,直到得到所需的答案。动态规划通常通过迭代循环实现计算,不使用递归。
通过以上层次的分析进一步理解带有备忘录的递归算法的优势,并将其与动态规划进行对比,有助于深入理解动态规划思想的应用。
方式三:动态规划
java实现
public class Fibonacci {public static long fibonacci(int n) {// 创建一个数组来存储子问题的解,初始值为0long[] dp = new long[n + 1];// 初始化前两个数的值dp[0] = 0;dp[1] = 1;// 从第三个数开始迭代计算for (int i = 2; i <= n; i++) {// 通过状态转移方程计算当前数的值dp[i] = dp[i - 1] + dp[i - 2];}// 返回第n个数的值return dp[n];}public static void main(String[] args) {int n = 20;long result = fibonacci(n);System.out.println("The Fibonacci number at position " + n + " is: " + result);}
}说明:
创建一个数组dp来保存子问题的解,数组的长度为n + 1,初始值都为0。 初始化数组中的前两个数,即dp[0] = 0和dp[1]= 1,这是斐波那契数列的基础情况。 从第三个数开始,使用循环迭代计算每个数的值。通过状态转移方程dp[i] = dp[i - 1] + dp[i - 2],计算当前数的值,即前两个数之和。 最后,返回第n个数的值,即为斐波那契数列中第n个数的结果。```
通过绘制 DP Table,可以更好地理解动态规划解法。而且你会发现,DP Table 实际上与带有备忘录的递归解法中的「备忘录」非常相似,只是顺序相反而已。事实上,当备忘录完成填充后,就形成了这个 DP Table。因此,这两种解法在很大程度上是相似的,而且在大多数情况下,它们的效率也基本相同。
在这里,我们引入了「状态转移方程」这个名词,实际上它描述的是问题结构的数学形式:
F(n) = F(n-1) + F(n-2)
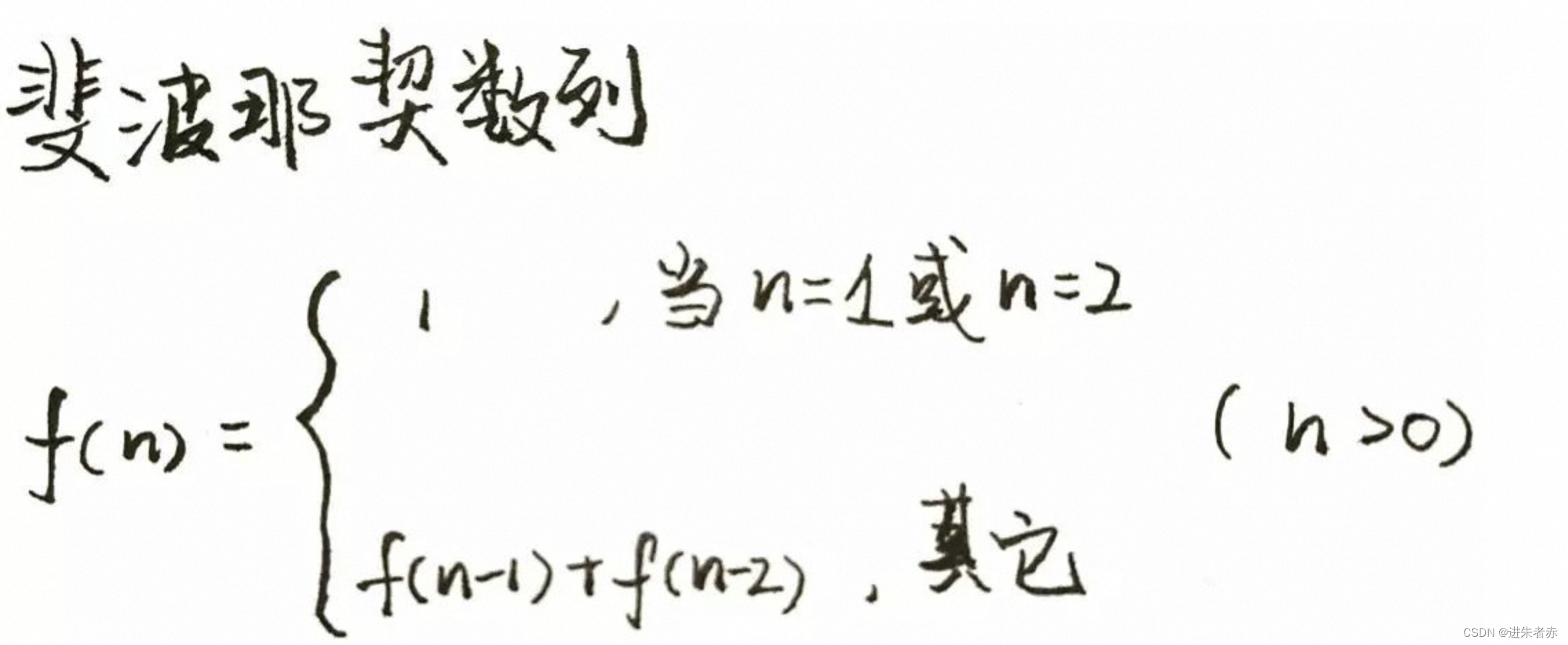
这个方程告诉我们,要计算第 n 个斐波那契数,我们只需要知道前两个数的值即可。通过这个方程式,我们可以将问题的求解转化为子问题的求解。
「状态转移方程」这个术语可能听起来有些高级,其实它的含义很简单。在斐波那契数列问题中,我们将 f(n) 看作是一个状态 n,而这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来。所以,「状态转移方程」就是描述问题中不同状态之间的变化关系而已。它帮助我们理解问题的结构并找到解决方法。
动态规划的精髓就是找到合适的状态转移方程,它能够将大问题拆分成小问题,并且小问题的结果可以用于求解大问题。在斐波那契数列问题中,状态转移方程适用于计算任意位置的斐波那契数。
因此,通过定义好状态转移方程并利用它,我们可以构建出 DP Table 或使用递归加备忘录的方式来高效地求解斐波那契数列问题。
这只是一个简单的示例,实际的动态规划问题可能会更复杂。但遵循这个解题套路框架,通过确定状态、定义状态转移方程、处理边界条件、计算动态规划数组和返回结果,可以更好地解决各种不同类型的动态规划问题
推荐练手题目
| 序号 | 题目名称 | 题目描述 | 难度 | 题目链接 |
|---|---|---|---|---|
| 1 | 爬楼梯(Climbing Stairs) | 有n个台阶,每次可以爬1个或2个台阶,求爬到第n个台阶的所有可能的方法数。 | 简单 | LeetCode 70 |
| 2 | 最长递增子序列(Longest Increasing Subsequence) | 给定一个整数数组,找到其中最长的递增子序列的长度。 | 中等 | LeetCode 300 |
| 3 | 背包问题(Knapsack Problem) | 有一个背包可以容纳一定重量的物品,给定一组物品的重量和价值,选择一部分物品放入背包,使得选中的物品总重量不超过背包容量,同时总价值最大。 | 中等 | LeetCode 322 |
| 4 | 打家劫舍(House Robber) | 给定一列房屋,每个房屋中都有一定数量的金额,相邻的房屋不能同时被盗窃。求能够盗窃的最大金额。 | 简单 | LeetCode 198 |
| 5 | 解码方法(Decode Ways) | 给定一个只包含数字的非空字符串,判断是否有可能解码成字母组合。每个数字转换为对应的字母(A - 1,B - 2,…,Z - 26)。 | 中等 | LeetCode 91 |
相关文章:
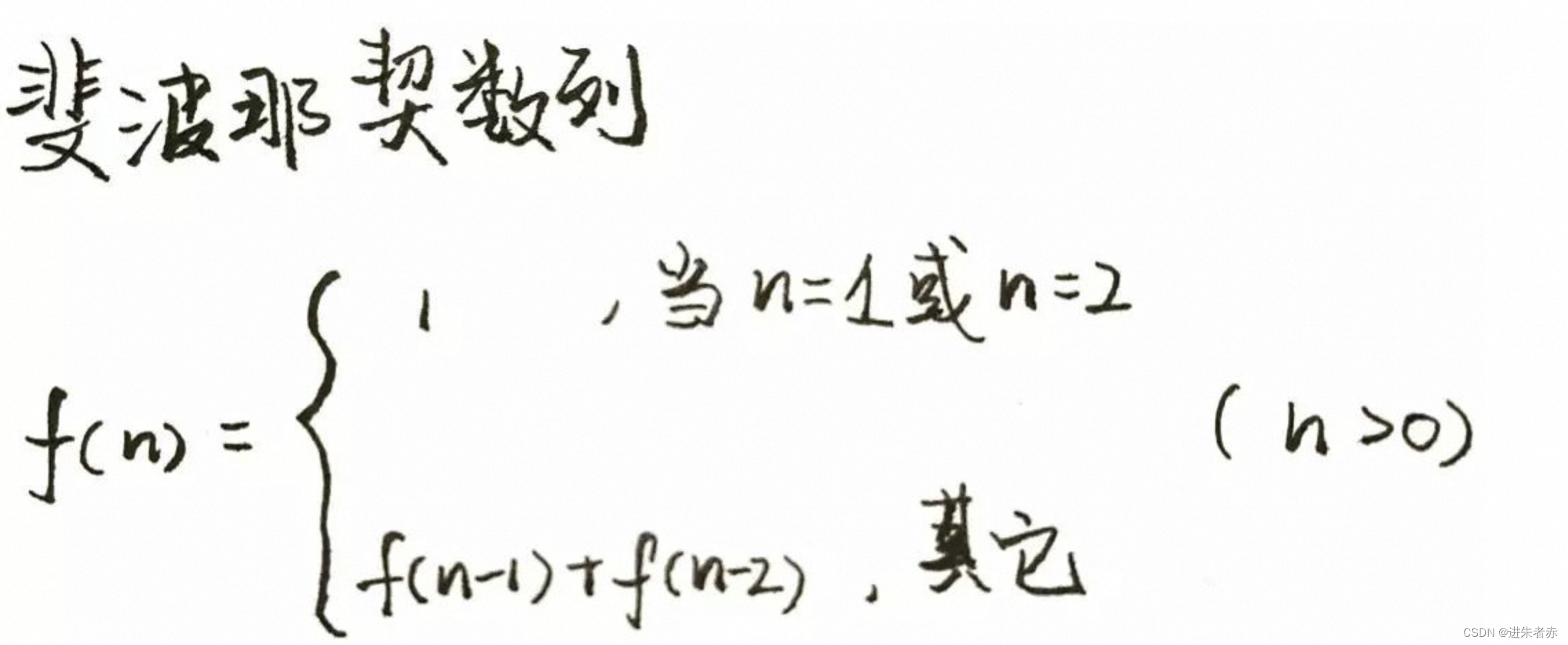
动态规划详解(Dynamic Programming)
目录 引入什么是动态规划?动态规划的特点解题办法解题套路框架举例说明斐波那契数列题目描述解题思路方式一:暴力求解思考 方式二:带备忘录的递归解法方式三:动态规划 推荐练手题目 引入 动态规划问题(Dynamic Progra…...

前端大额计算,真正解决js精度丢失问题
1.解决前端大额计算导致精度丢失问题 2.从底层上解决这个问题,计算时不使用js 运行时计算。 使用rust语言来解决这个问题,因为是底层语言,不涉及到精度问题。 3.实现步骤 步骤 1: 安装工具 确保你已经安装了Rust工具链和wasm-pack&#x…...
)
Android笔记--MediaCodec(一)
这一节主要来了解一下MediaCodec,Android MediaCodec 是 Android 平台提供的一个用于处理音频和视频数据的 API。它允许开发者对音频和视频数据进行编码和解码,支持多种格式和编解码器。MediaCodec API 通常用于实现实时音视频处理,如视频录制…...
Linux简单介绍
Linux简单介绍 编译器VMware虚拟机Ubuntu——LinuxOS为什么使用LinuxOS? 目录结构Windows目录结构Linux操作系统home是不是家目录? Linux常用命令终端命令行提示符与权限切换命令tab 作用:自动补全上下箭头pwd命令ls命令mkdir命令touch命令rm…...
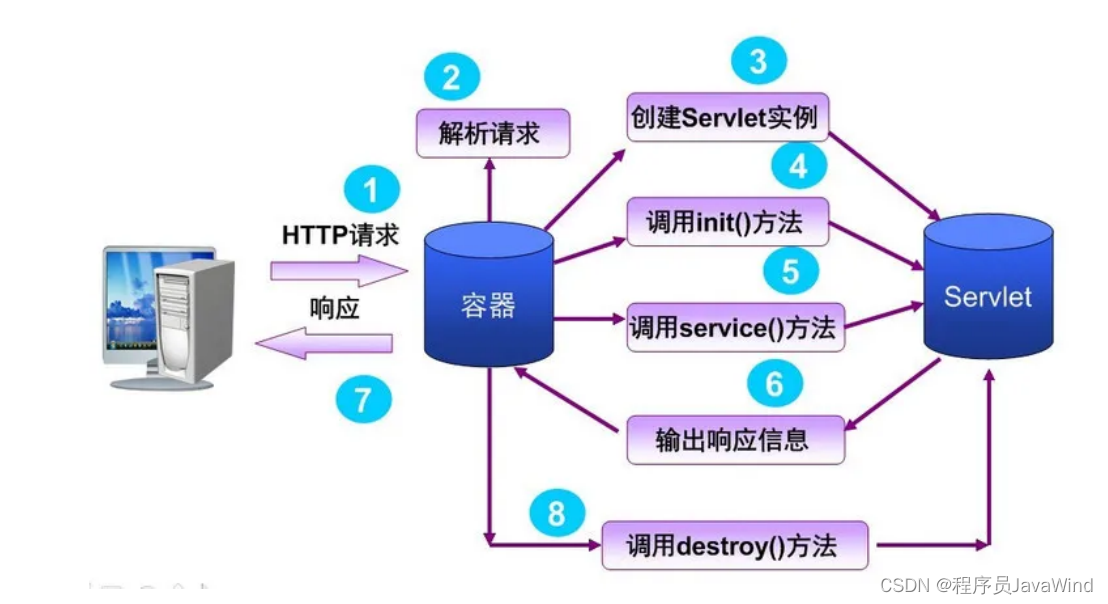
Servlet 的基本理解
Servlet 是JavaEE规范的一种,主要是为了扩展Java作为Web服务的功能,统一接口。由其他内部厂商如tomcat,jetty内部实现web的功能。如一个http请求到来:容器将请求封装为servlet中的HttpServletRequest对象,调用init()&a…...

JavaScript之applye、bind和call方法详解
Question Q1 apply()、bind()和call()方法的区别在哪? Q2 apply()和call()的应用场景 Q3 apply()、bind()和call()方法手写实现逻辑 来源 继承自Function.prototype,属于实例方法 console.log(Function.prototype.hasOwnProperty(call)) //trueconsole.l…...

Docker,anaconda环境的部署与迁移
功能上线将提上日程,但是如何将我windows环境下的程序放到linux服务器的测试环境跑通呢?这是我这整个清明假期将要解决的一件事,最蠢的办法就是看自己的环境下有哪些依赖,如何到服务器上一个一个下,但是首先这个方法很…...

【大数据运维】Hbase shell 常见操作
文章目录 一. DDL1. 表的DDL1.1. 创建表1.2. 删除表 2. 列族的DDL2.1. 增加一个列簇2.2. 删除列族2.3. 修改列族版本(ing) 二. DML1. 插入与更新数据2. 删除数据3. 清空表 三. DQL1. scan:查一批数据1.1. 查询全部1.2. 过滤rowkey1.3. 过滤列…...

LeetCode-217存在重复的元素
217 存在重复的元素 给定一个整数数组,判断是否存在重复元素。 如果存在一值在数组中出现至少两次,函数返回 true 。如果数组中每个元素都不相同,则返回 false 。 JavaScript的 Array 对象是用于构造数组的全局对象,数组是类似…...
基于两个单片机串行通信的电子密码锁设计
1.功能 电子号码锁在实际应用中应该有两部分,一部分在外部,有键盘部分和密码显示;另一部分内部,设置密码、显示密码。使用单片机自身带有的串口可以很方便的实现单片机之间的通信,使输入的密码值传送到主机检验是否是…...
之产品设计)
产品经理功法修炼(3)之产品设计
点击下载《产品经理功法修炼(3)之产品设计》 1. 前言 产品经理的能力修炼并非局限于某一技能的速成,而是需要全面参与到产品的整个生命周期中,通过不断的实践来逐步提升自己的各项能力。尽管在企业的日常运作中,我们不可能身兼数职去扮演每一个角色,但作为产品的核心负…...

Qt 的发展历史、现状与启示
Qt 最早在1991年由挪威的两位程序员 Eirik Chambe-Eng 和 Haavard Nord 开发,他们在1994年创立 Trolltech 公司(奇趣科技)正式经营软件业务。Qt 的第一个公众预览版于1995年面世,之后在2008年被诺基亚收购;2011年到201…...
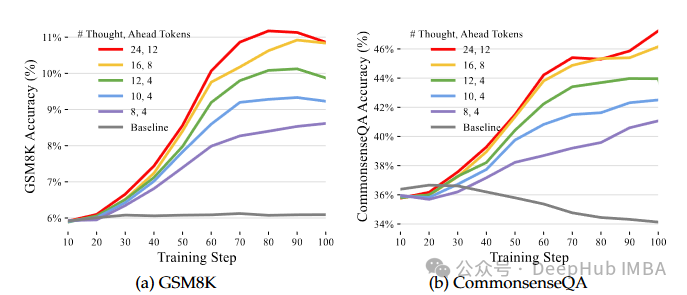
Quiet-STaR:让语言模型在“说话”前思考
大型语言模型(llm)已经变得越来越复杂,能够根据各种提示和问题生成人类质量的文本。但是他们的推理能力让仍然是个问题,与人类不同LLM经常在推理中涉及的隐含步骤中挣扎,这回导致输出可能在事实上不正确或缺乏逻辑。 考虑以下场景:正在阅读一…...

【Kotlin】匿名类和伴生类
1 匿名类 1)无继承 fun main() {var obj object {var name: String "zhang"override fun toString(): String {return name}}println(obj) // zhang } 2)有继承 fun main() {var obj object: People {var name: String "zhang"…...
决策树)
【机器学习算法介绍】(3)决策树
决策树是一种常见的机器学习算法,用于分类和回归任务。它模拟了人类决策过程,通过一系列的问题来引导决策。决策树的构建涉及三个主要步骤:特征选择、树的构建和树的剪枝。 1. 特征选择 特征选择是决策树构建过程中的第一步,目的…...

算法之查找
1、顺序查找: package com.arithmetic.search; //顺序查找 //sequentialSearch 方法接收一个整数数组和一个目标元素作为参数,并使用顺序查找的方式在数组中查找目标元素。 //它通过循环遍历数组元素,逐个与目标元素比较,如果找到…...

LInux脚本学习
1.注释 #单行注释 以 # 字符开头就是单行注释 当然第一行除外,比较特殊 2.多行注释 3.Shell文件的作用 Shell文件就是linux命令集 4.sh脚本的执行方式 bash xxx.sh 5.新建的文件会没有执行权限 #为文件赋予执行权限 chmod ux xxx.sh 6.编写规范 #!/bin/bash #…...
)
JavaWeb基础(计网 socket 数据库 JDBC lombok Mybatis JUnit Maven)
本文用于检验学习效果,忘记知识就去文末的链接复习 1. 网络基础 1.1 计网基础 区分设备:IP地址 区分网络:网络地址 网络互联:路由器 主机上进程间通信:端口 http是常用的协议,基于TCP协议 TCP VS U…...
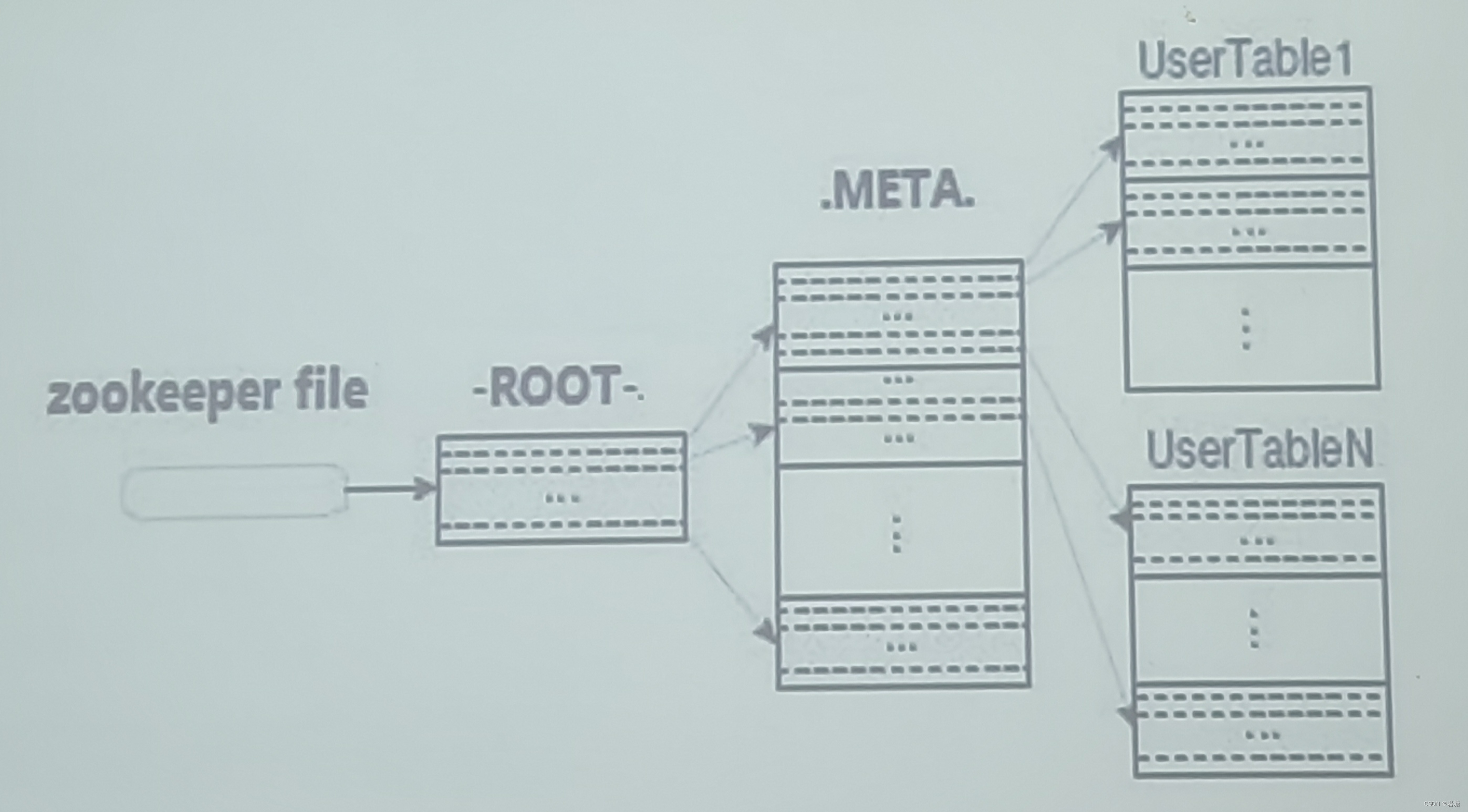
【HBase】
什么是HBase HBase是Google Bigtable的开源实现,类似Google Bigtable利用GFS作为其文件存储系统,HBase利用Hadoop HDFS作为其文件存储系统;Google运行MapReduce来处理Bigtable中的海量数据,HBase同样利用Hadoop MapReduce来处理HBase中的海量数据。 访问层次(数据…...

Vue3:使用Pinia存储、读取、修改数据
一、存储数据 Pinia插件中,存储数据的配置项是state count.ts import {defineStore} from piniaexport const useCountStore defineStore(count,{// 真正存储数据的地方state(){return {sum:6}} })loveTalk.ts import {defineStore} from piniaexport const use…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...
