自动驾驶之心规划控制笔记
Search-based Path Planning Methods
Path Finding Problem
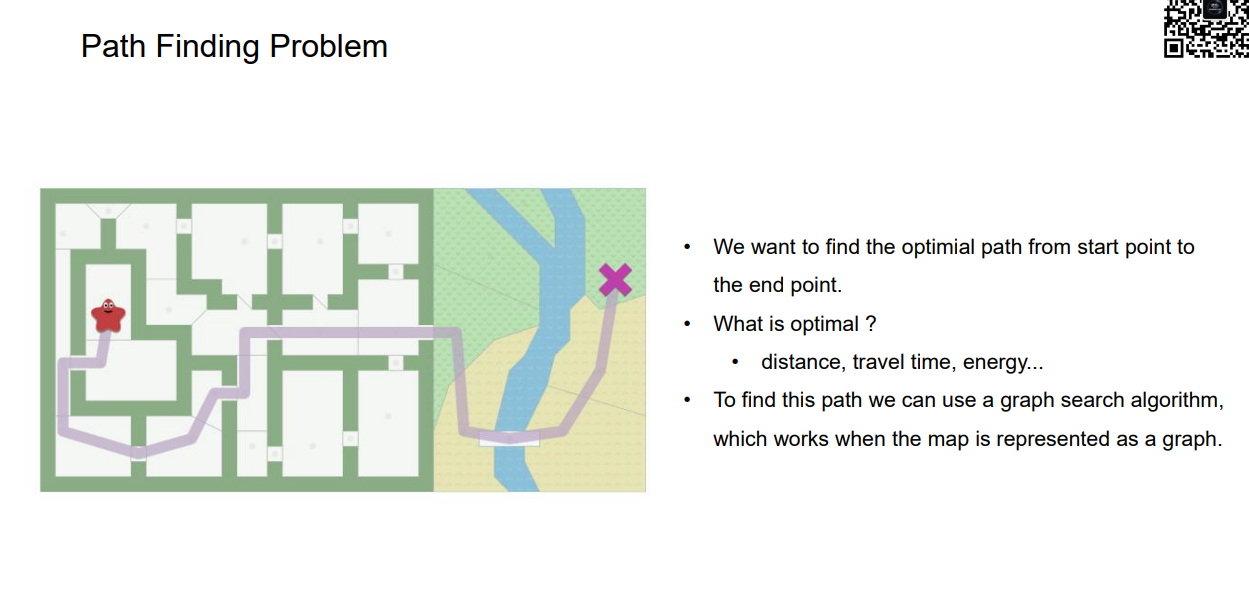
一般来说指标有距离,耗费时间,能量,或者多目标。
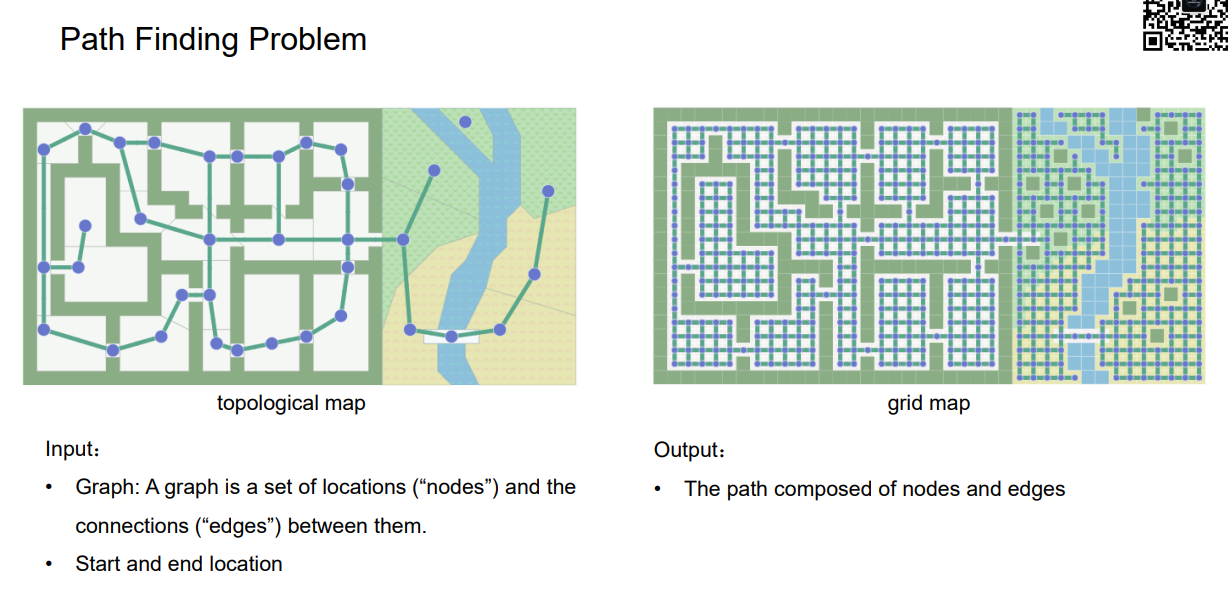
左图是拓扑地图,蓝色的点就是顶点,绿色的线是连接关系。最后得到的是一个从哪里走的一个最优,并非精细解。
右图是栅格地图,这个搜索出来的是在相对分辨率比较高的情况下的最优路径。
路径搜索问题的输入输出是什么:
输入:给出一副由节点和边构成的图论上的图,起点和终点
输出:返回一条由节点和边组成的path
Graph Basic
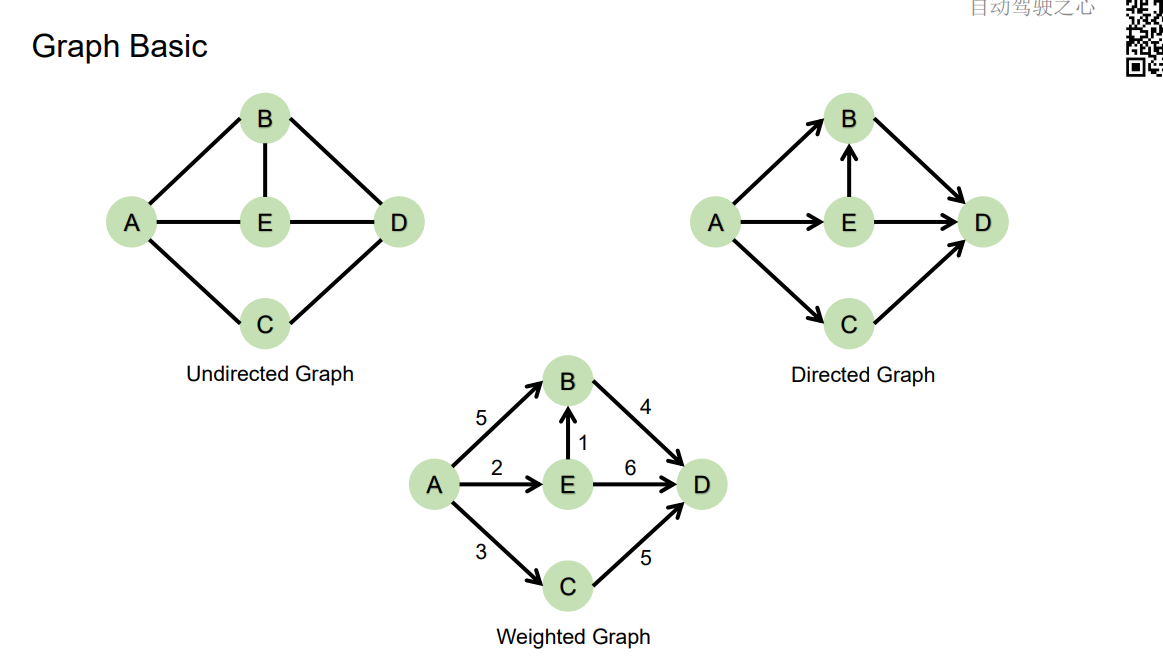
无向图(可以从节点A-B,也可以B-A)、有向图(可以从A-B,但是不可以B-A)、带权重的图(有了每条边的代价,来定义哪条路最优)
Some ways to Construct Graph
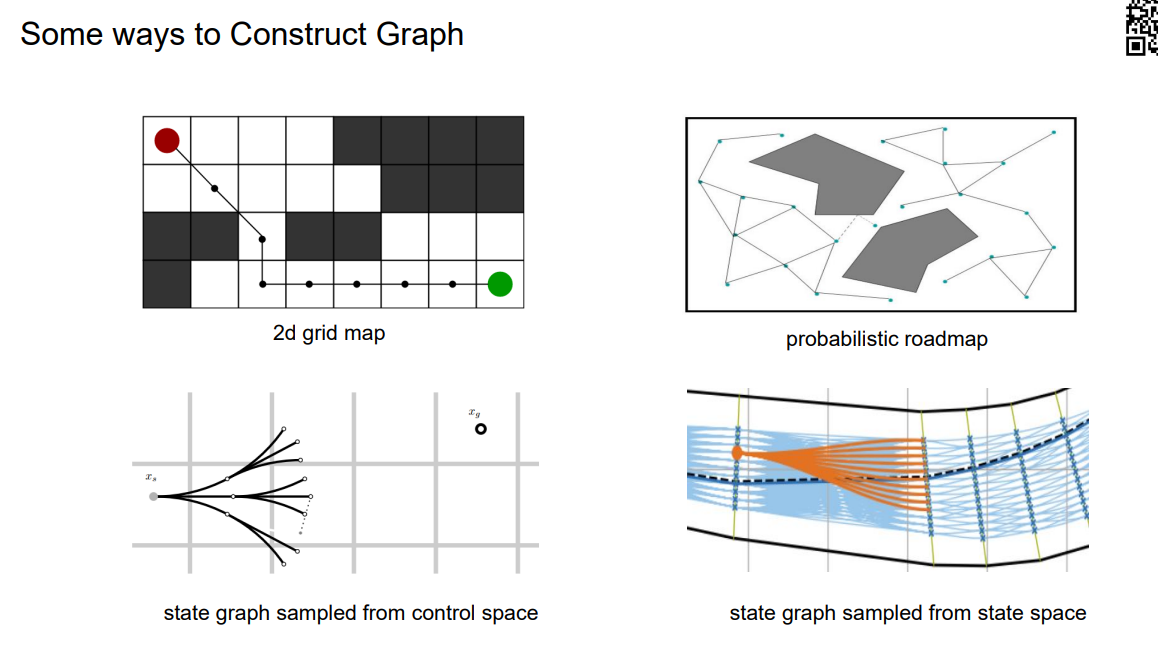
基于实现的效果来定制图。
栅格地图:每个顶点就描述栅格中心世界坐标系下的坐标,有天然的连接关系,与周围八个节点天生连接。
概率路图:通过采样得到的,采样顶点,通过规则,选择边。
state graph sampled from control space :运动基元构成的,给定转角和速度,通过积分的方式得到一小段轨迹。
state graph sampled from state space:给定起点终止顶点,根据逆动力学来构造运动基元。
Graph Traversal Algorithm
BFS
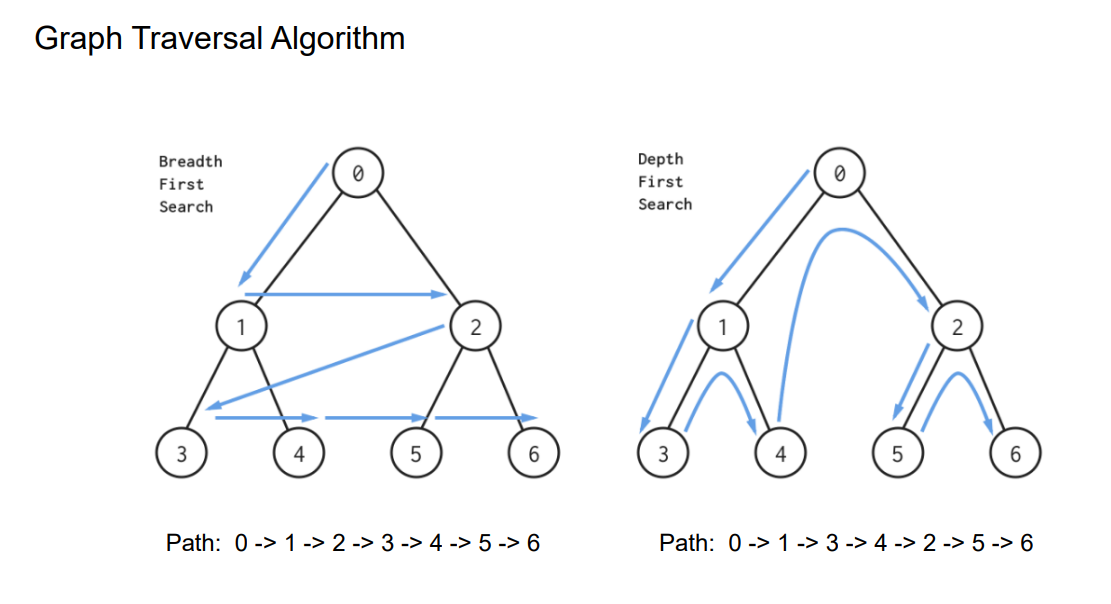


队列,先进先出,层序遍历。
算法输入是:一幅图,起始节点、终止节点。
输出是:从终点回溯到起点的最短路径。
步骤:先定义队列Q,然后把起始节点加入到队列中,然后把起始节点标记成已访问。
主循环:终止条件:队列Q没有节点,也就是所有节点都访问过了,另外一个条件式访问的节点是终点。
弹出队列的第一个节点,依次访问节点周围的邻居节点,如果节点没有访问过,就把节点加入到队尾中,并且把父节点标记成当前节点,并且把这个节点标记成已访问的状态。不断循环,就可以遍历到所有节点,如果存在可行路径,一定能找到。
BFS Search Process
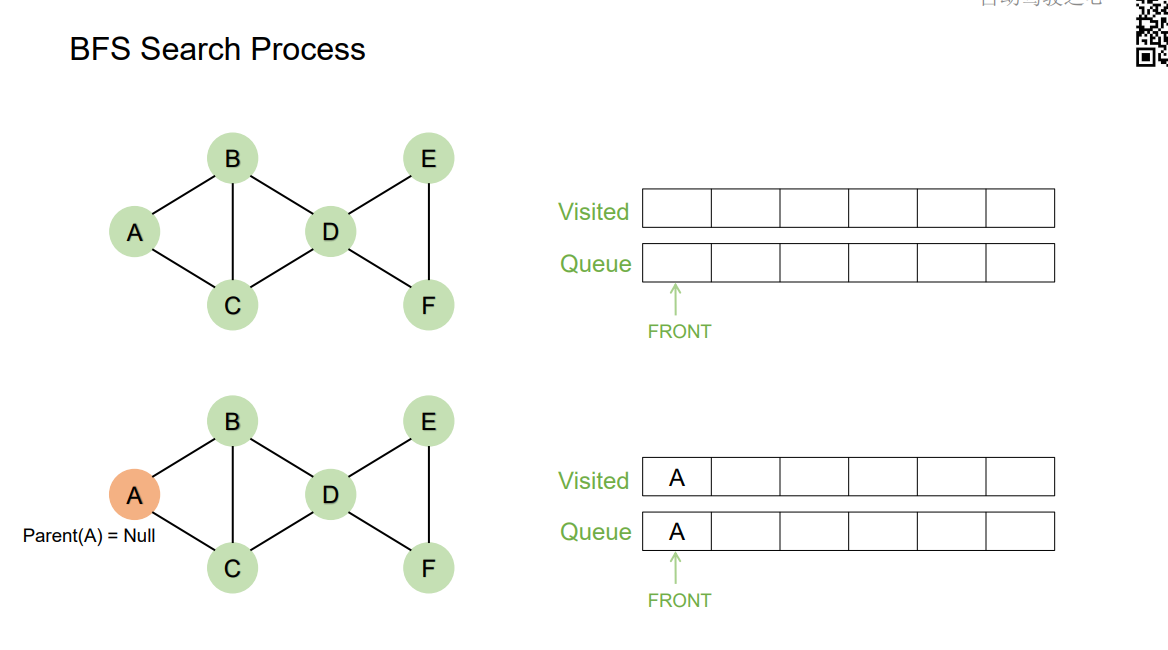
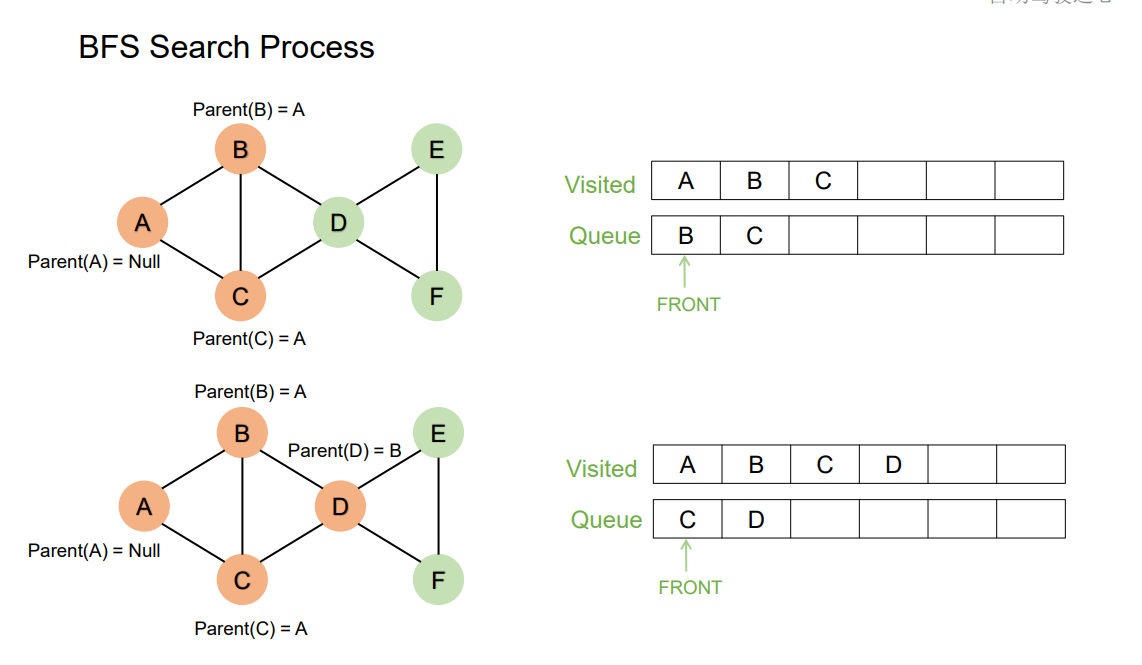
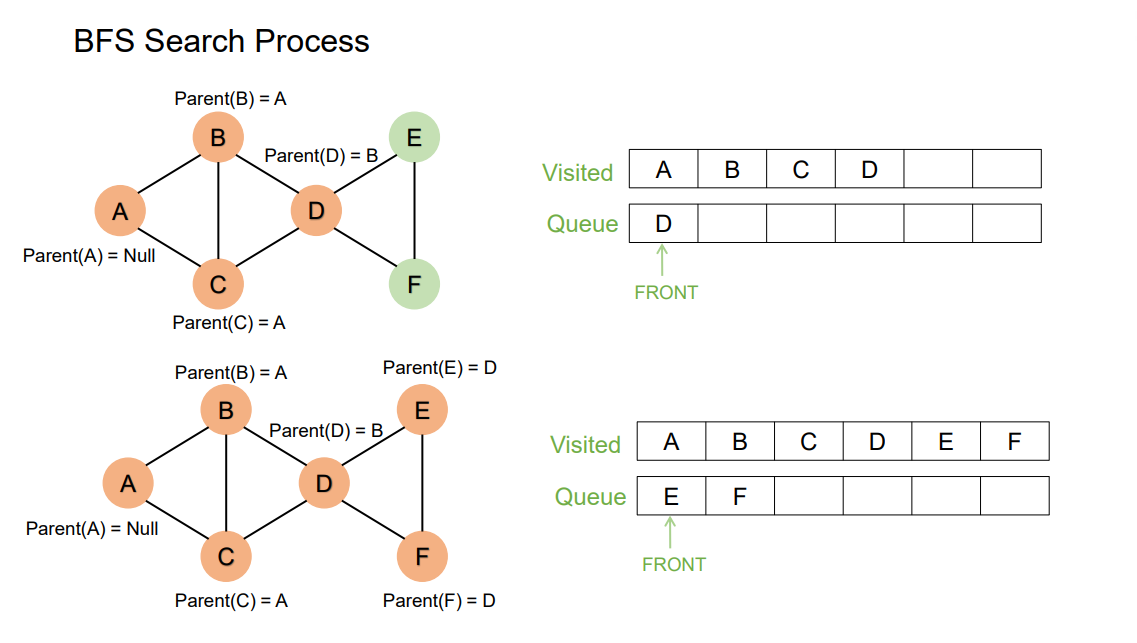
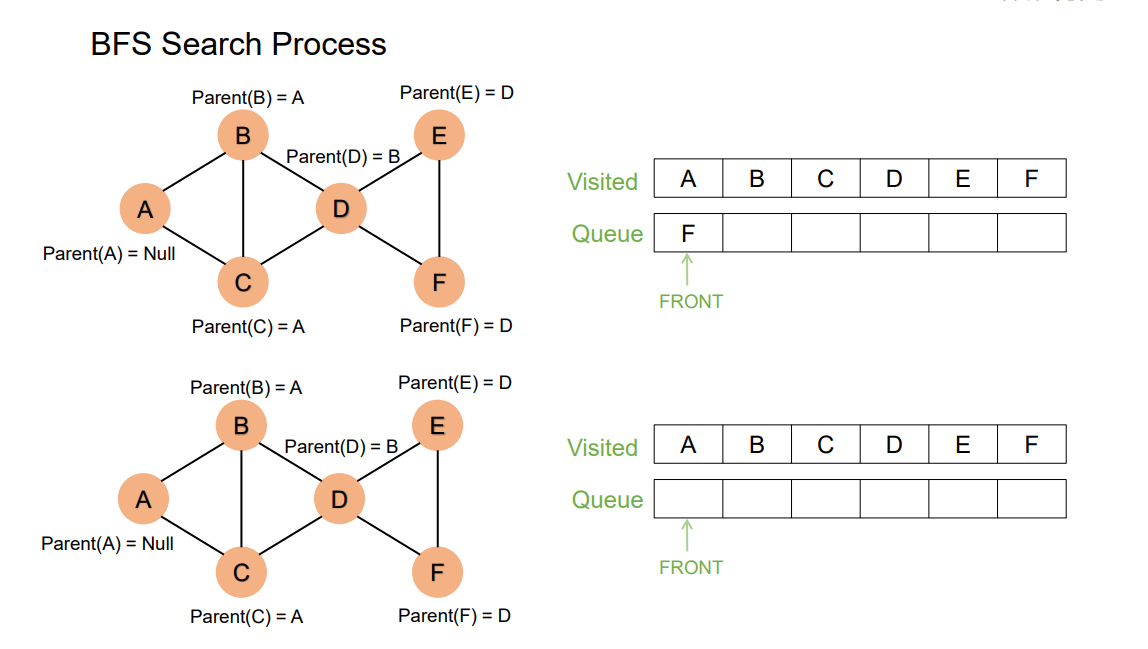
Summary

1、会相同的探索所有的方向
2、如果所有边的权重为1,那么BFS搜索出来的路径就是cost最优的路径。
Dijkstra

维护了一个新的变量g(n),g(n)是从起始节点到当前节点n累计的代价,访问的是在openset中累计代价最小的那个节点去访问,采用贪心的思想。
Priority queue

优先级队列,为容器赋予优先级。
Algorithm Dijkstra

输入:有个图,有个起点的节点和终点节点
输出:一条从终点节点向起点节点回溯得到的最短路径
Dijkstra Search Process
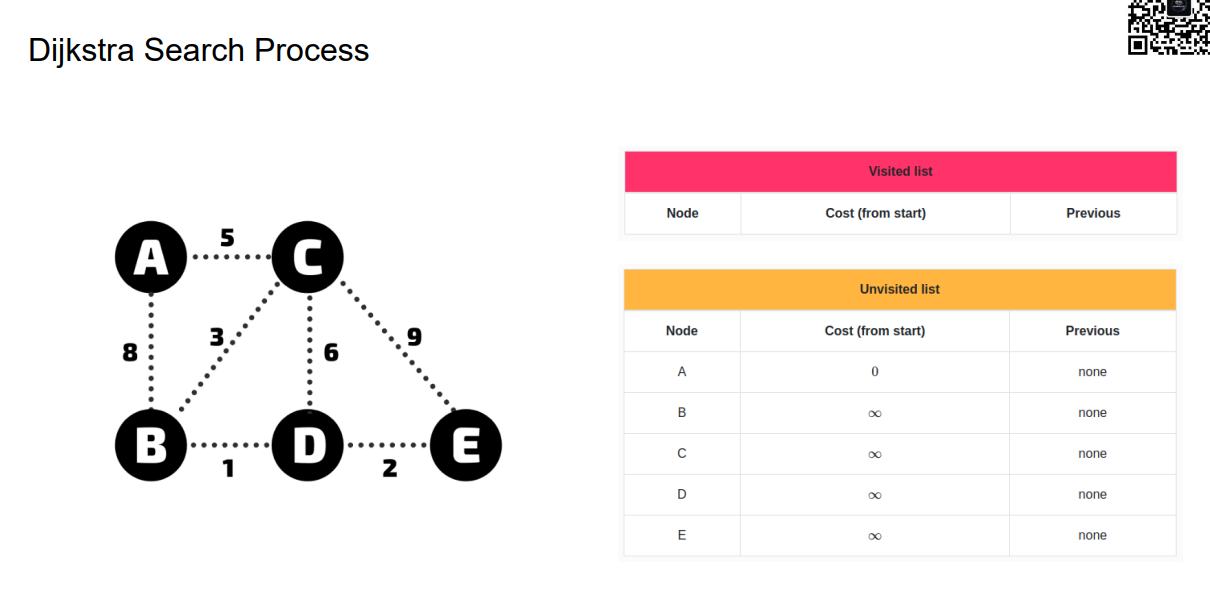
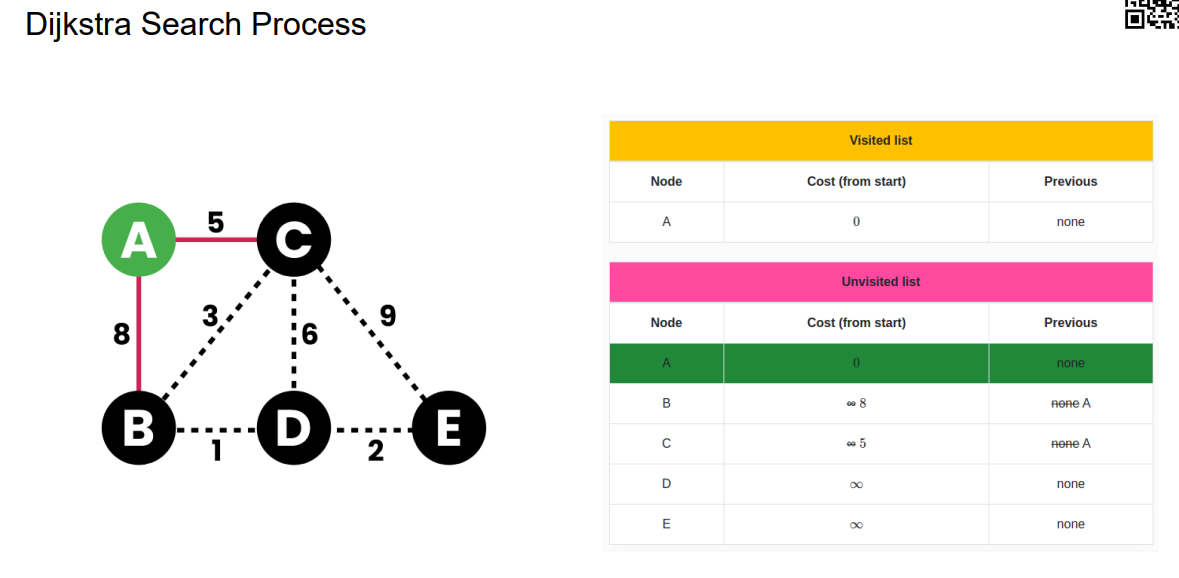



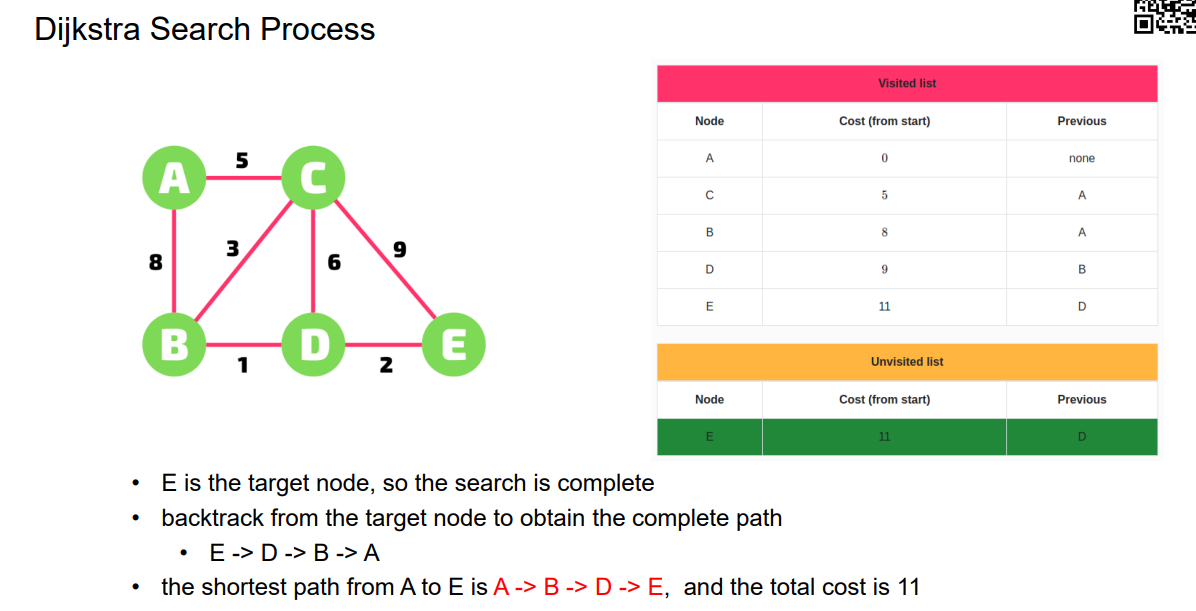
Summary

优点:
1、可以获得到起点到任何节点的最短路径
2、满足最优性
缺点:
1、无启发函数
A* Algorithm
Core ideas

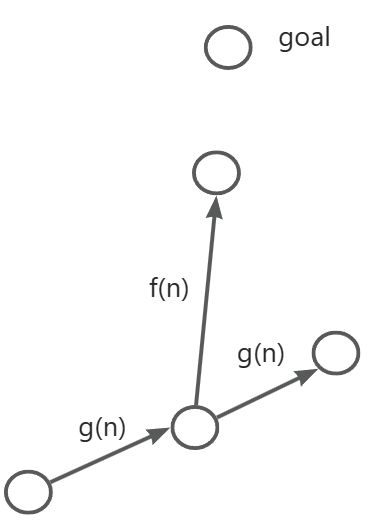
Dijkstra在搜索的过程中是不知道终点信息的,搜索效率不高。A*算法设计一个到目标点的启发式函数,此时用f来描述每个节点的cost(f = g + h)。
这里可以简单的画个图,如图所示,Dijkstra会浪费一部分计算资源去扩展与终点较远的节点,对于A*算法会更有目的性一些。
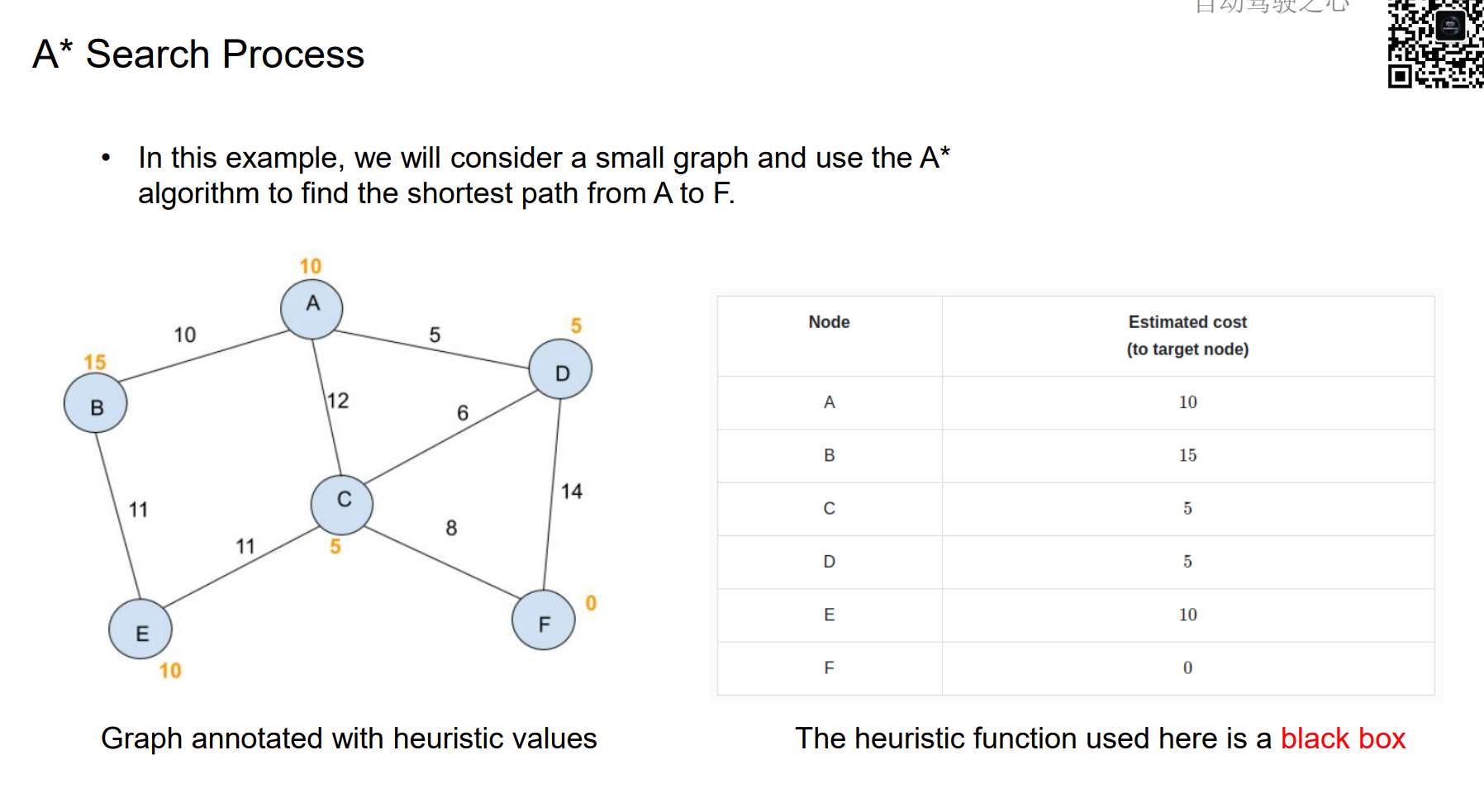
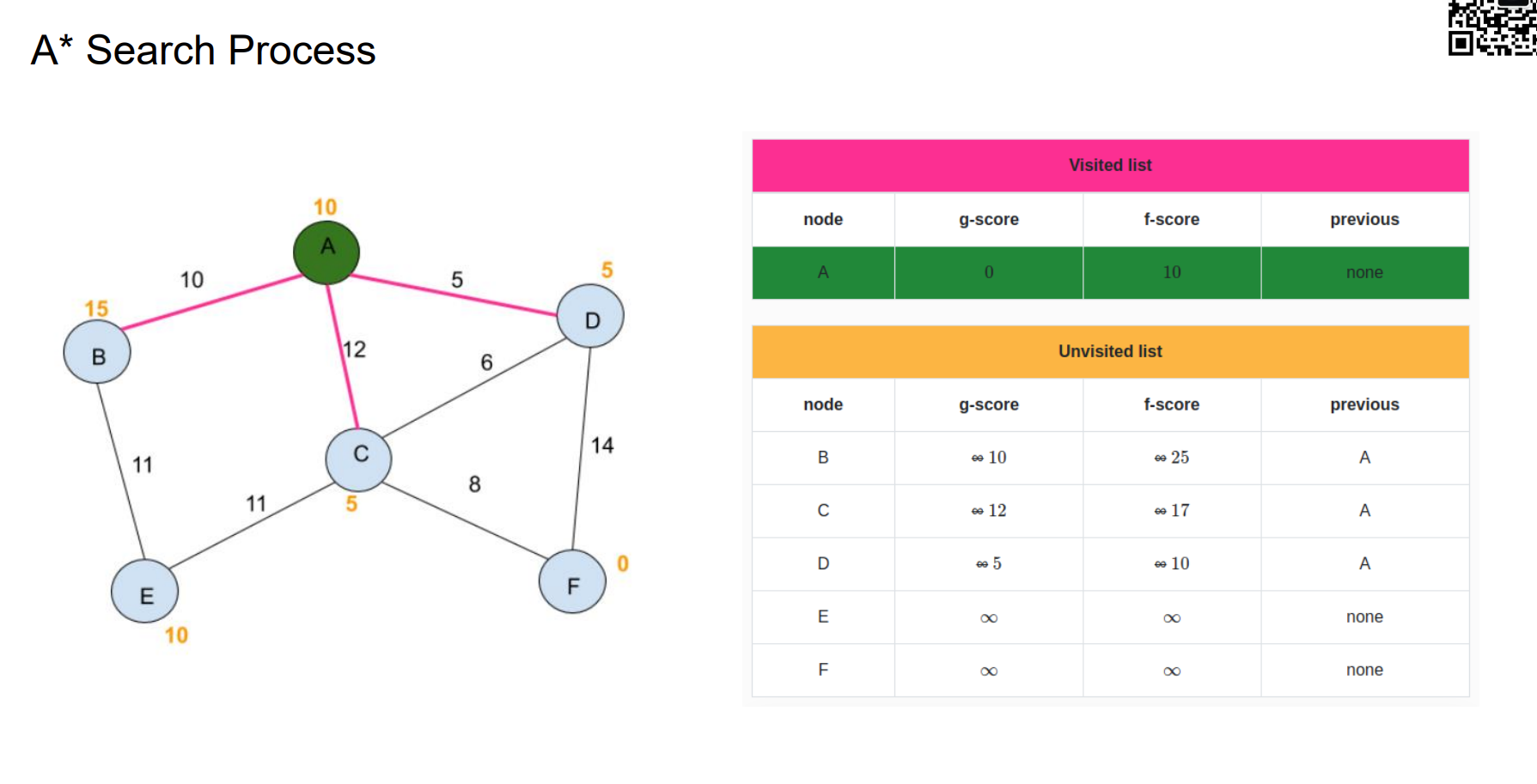
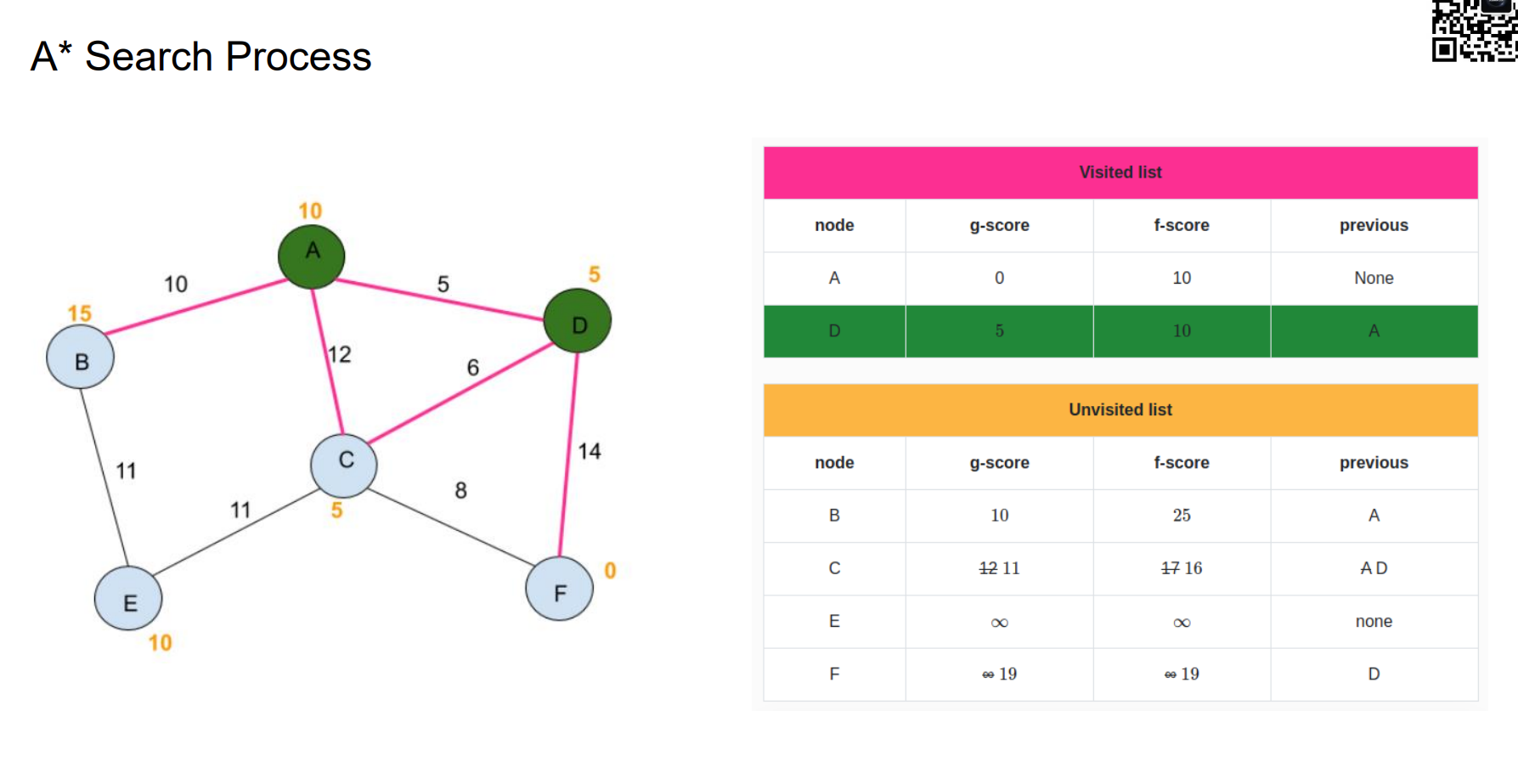
A* Search Process


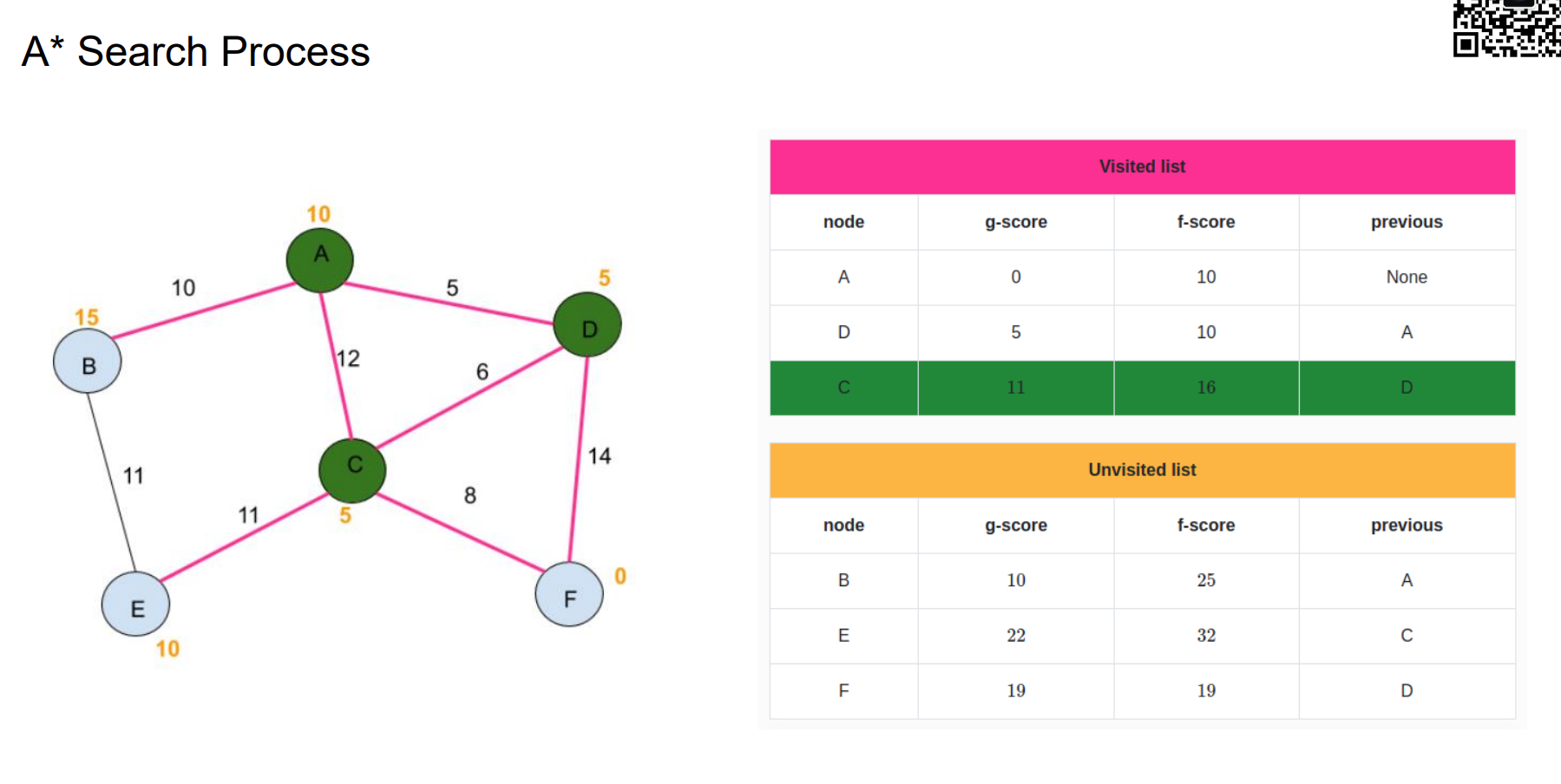
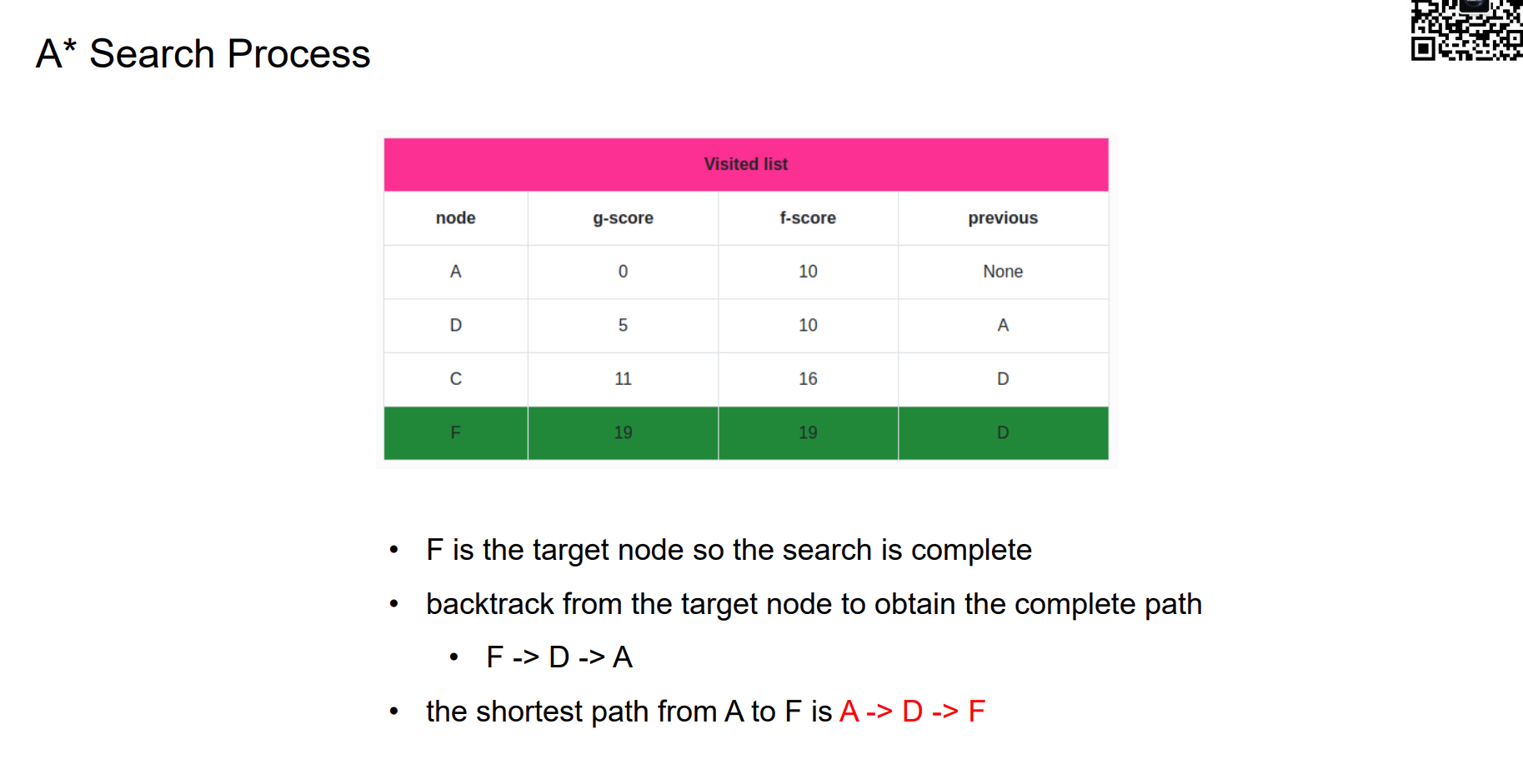
Heuristic Function Design

启发式函数的设计和具体任务有关系,如果说搜索问题的最优指标和距离有关系的话,那么可以用下面这几种距离来定义启发式函数。

Euclidian distance其实对应的是一个二范数,在几何上就是直线距离。
Manhattan distance在数学上就是一范数。
Great circle distance描述的是球面上两点的最短路径,对应于是弧长的概念。
Optimality

如何设计启发式函数能保证A*算法的最优性:heuristic function不能高于costs。也就是估计值需要小于真实值。如果满足这一点,那么A*算法一定能找到最优解的,且比Dijkstra快。
What’s Wrong with Overestimated Heuristics?
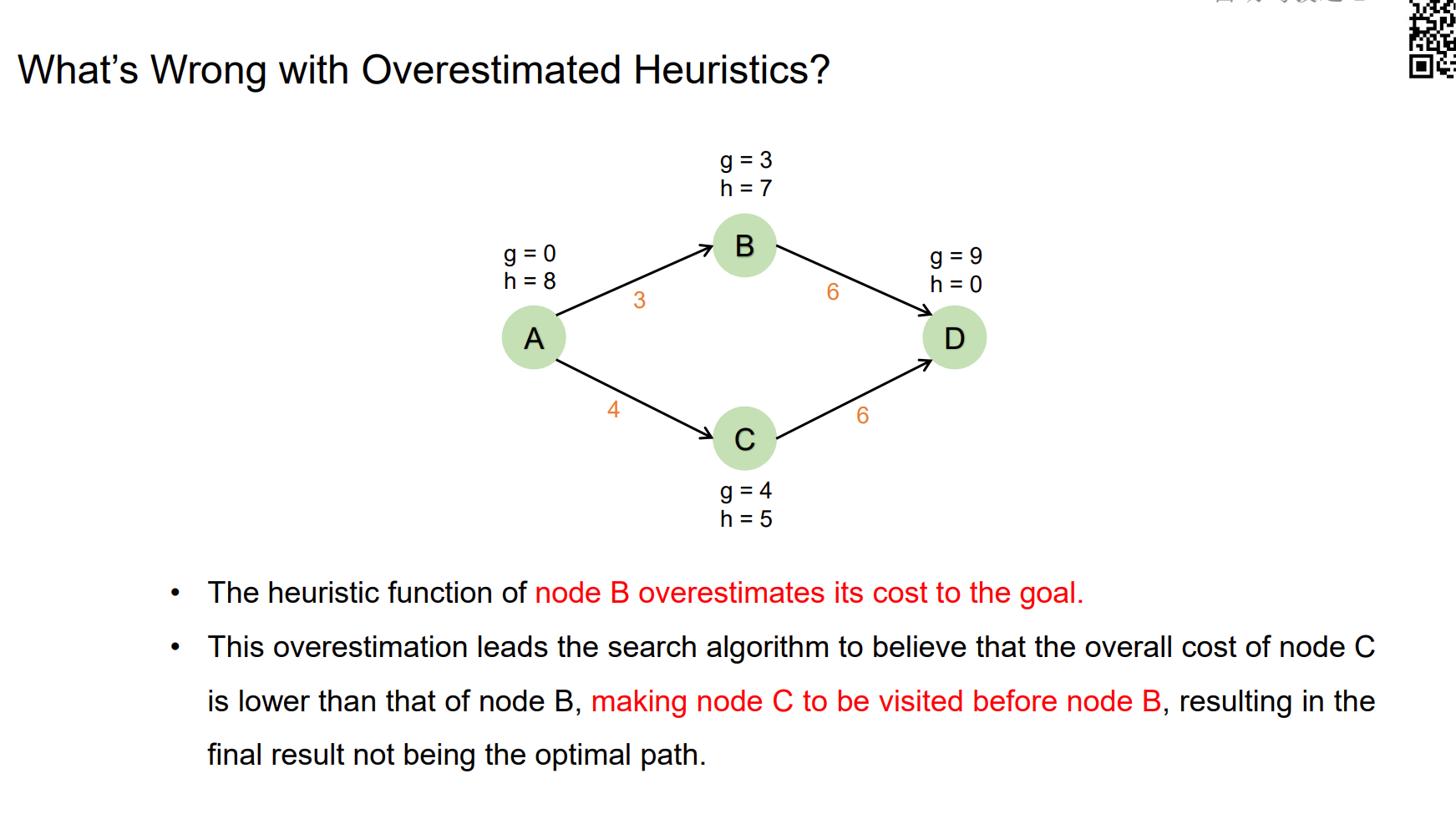
对于上图而言,根据A*的逻辑,选择ACD这个路径,但是真实情况是ABD的代价最小,出现这样的计算错误是由于B的h值大于真实的cost。
Heuristic Function Design in Gridmap
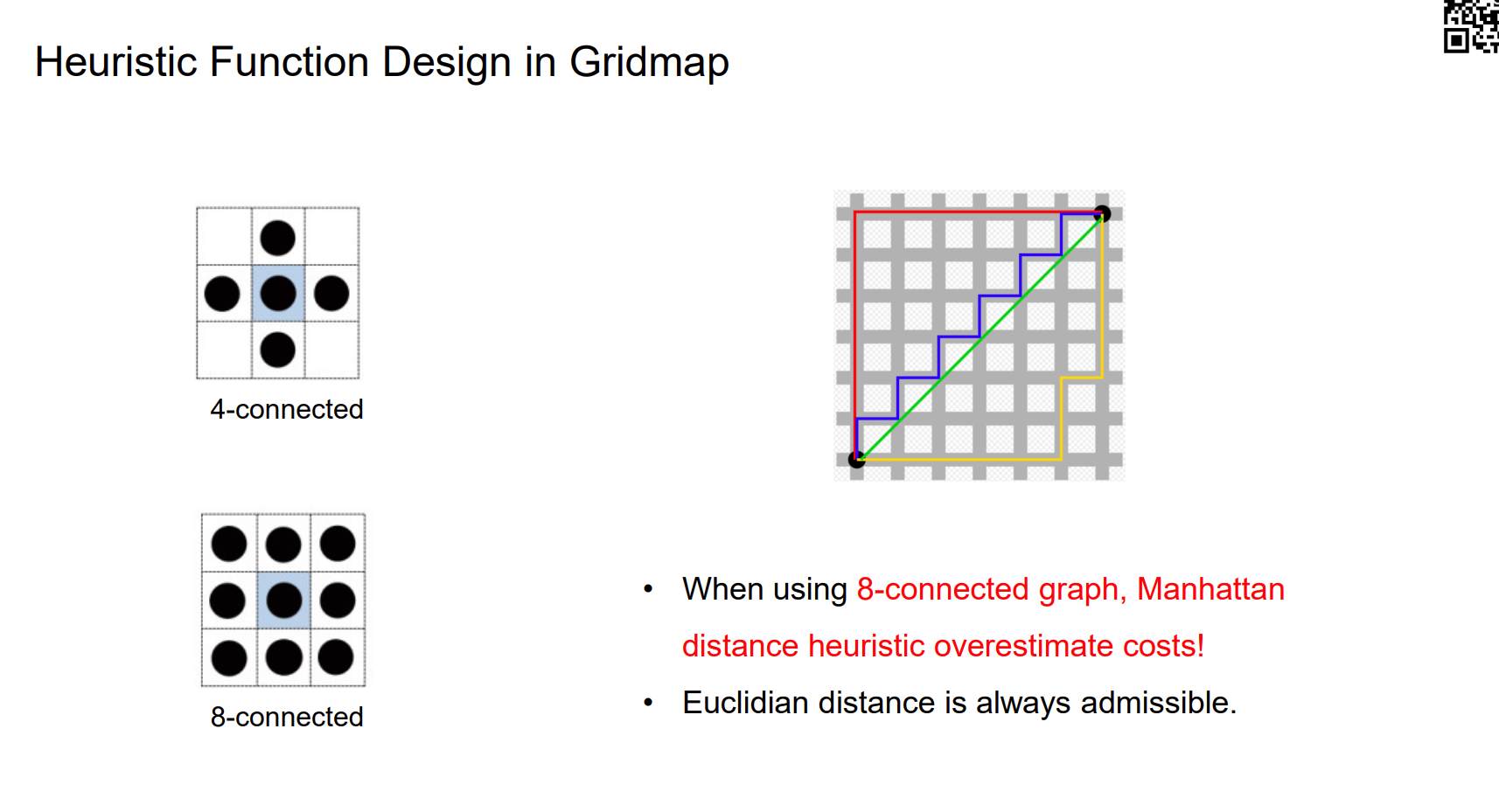
对于八连通的形式,用Manhattan distance会高估cost,可能导致找不到最优解。欧式距离可以使用。
Efficiency and Accuracy
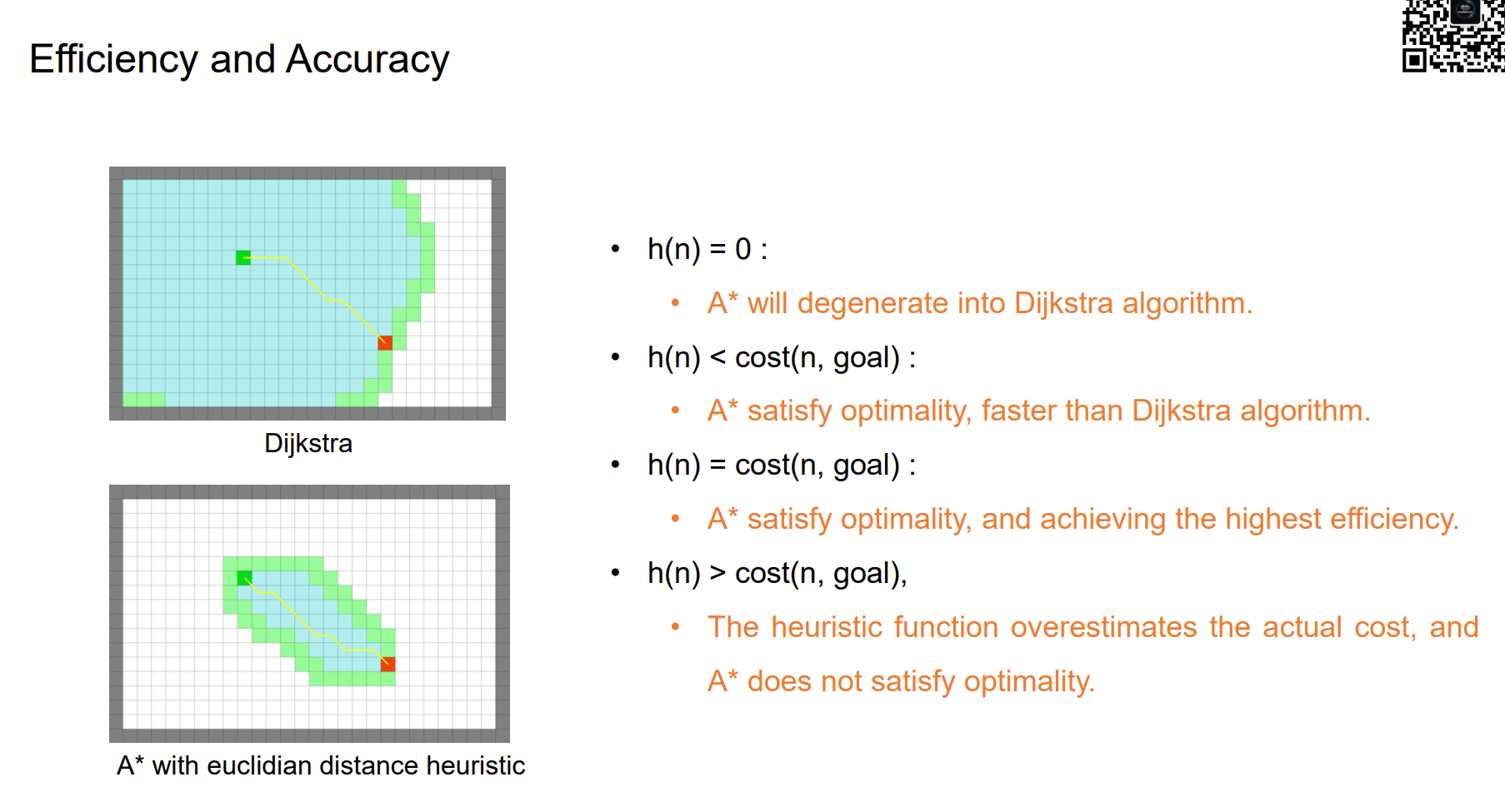
Summary

Dynamic Programming
What is Dynamic Programming

对于一个动态规划的问题,具有
1、有一个最优的子结构
2、对于所有的子问题,有很多是重复的。(这里相当于,如果一个子问题之前计算过了,那么就将结果保存起来,后续可以通过查表的形式,不用重复计算)
Tiny Example of Dynamic Programming

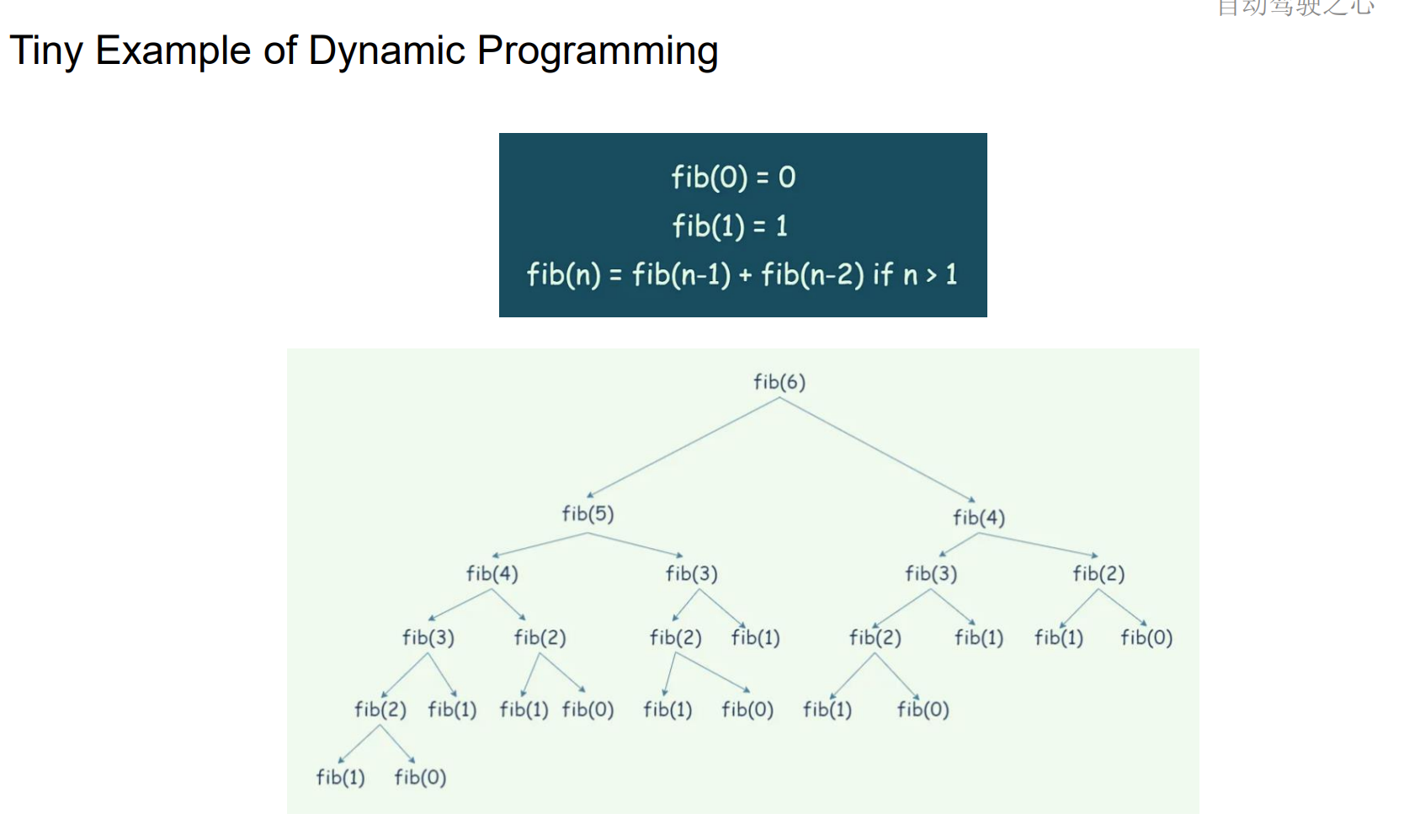
Dynamic Programming in Path Search
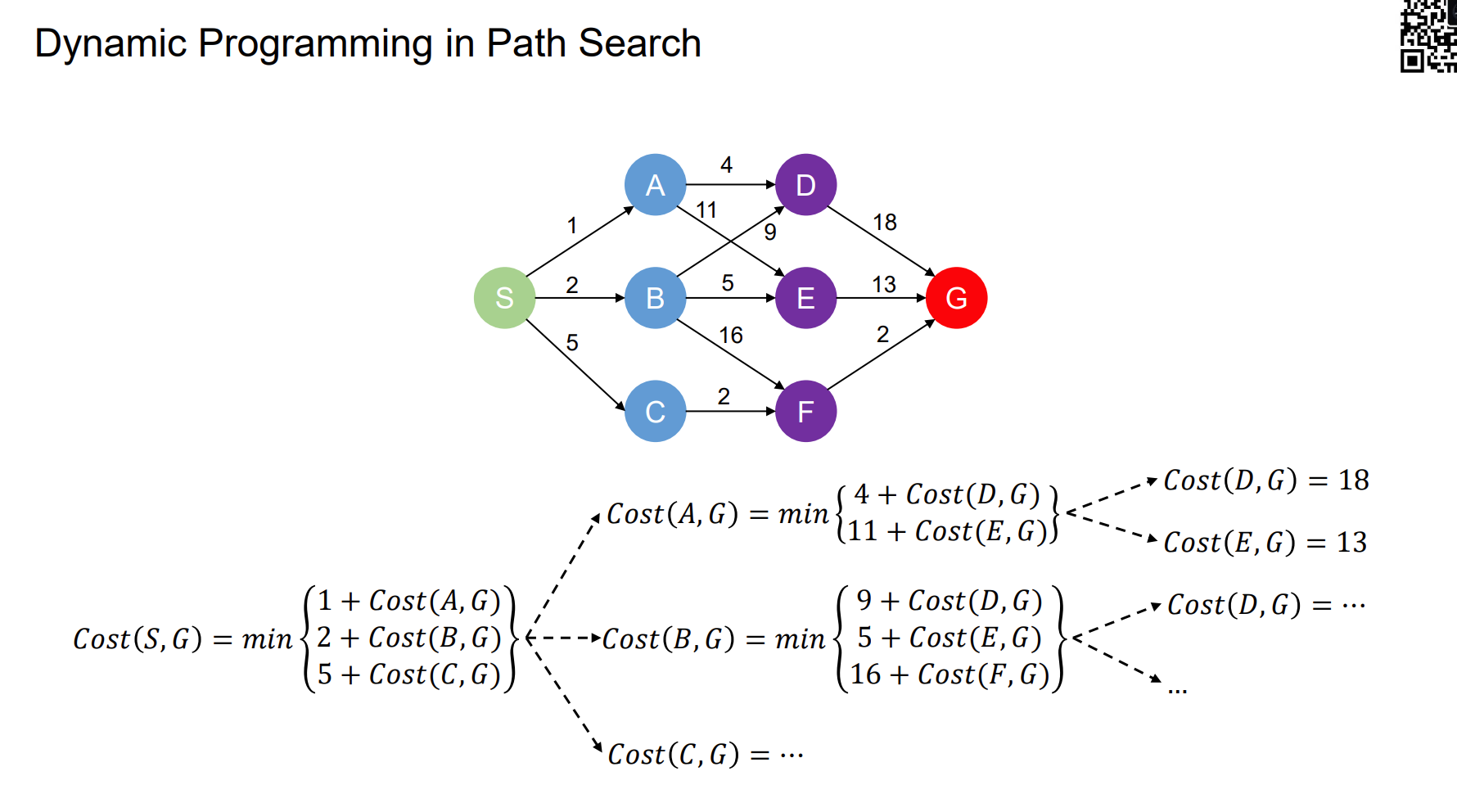
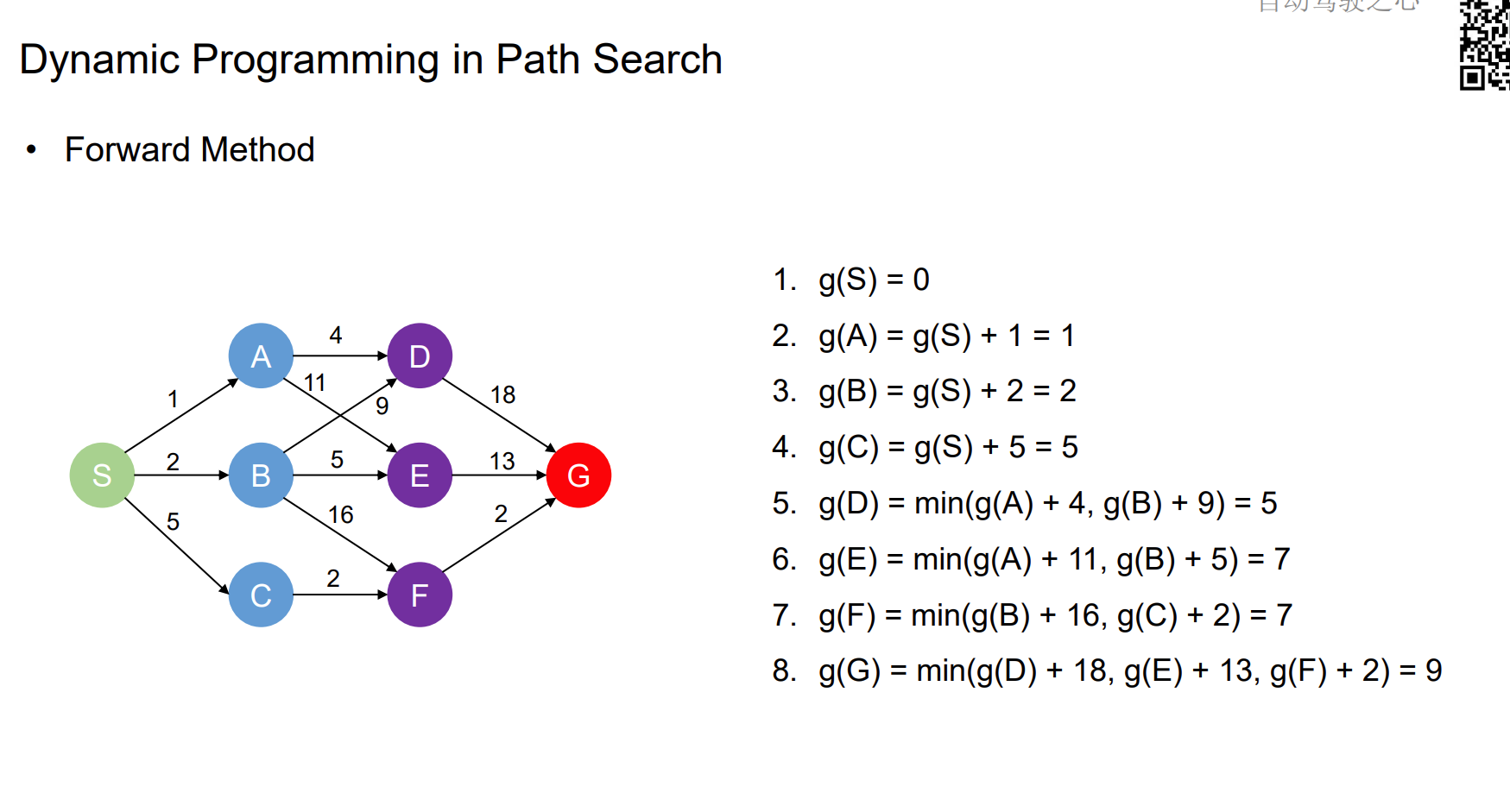
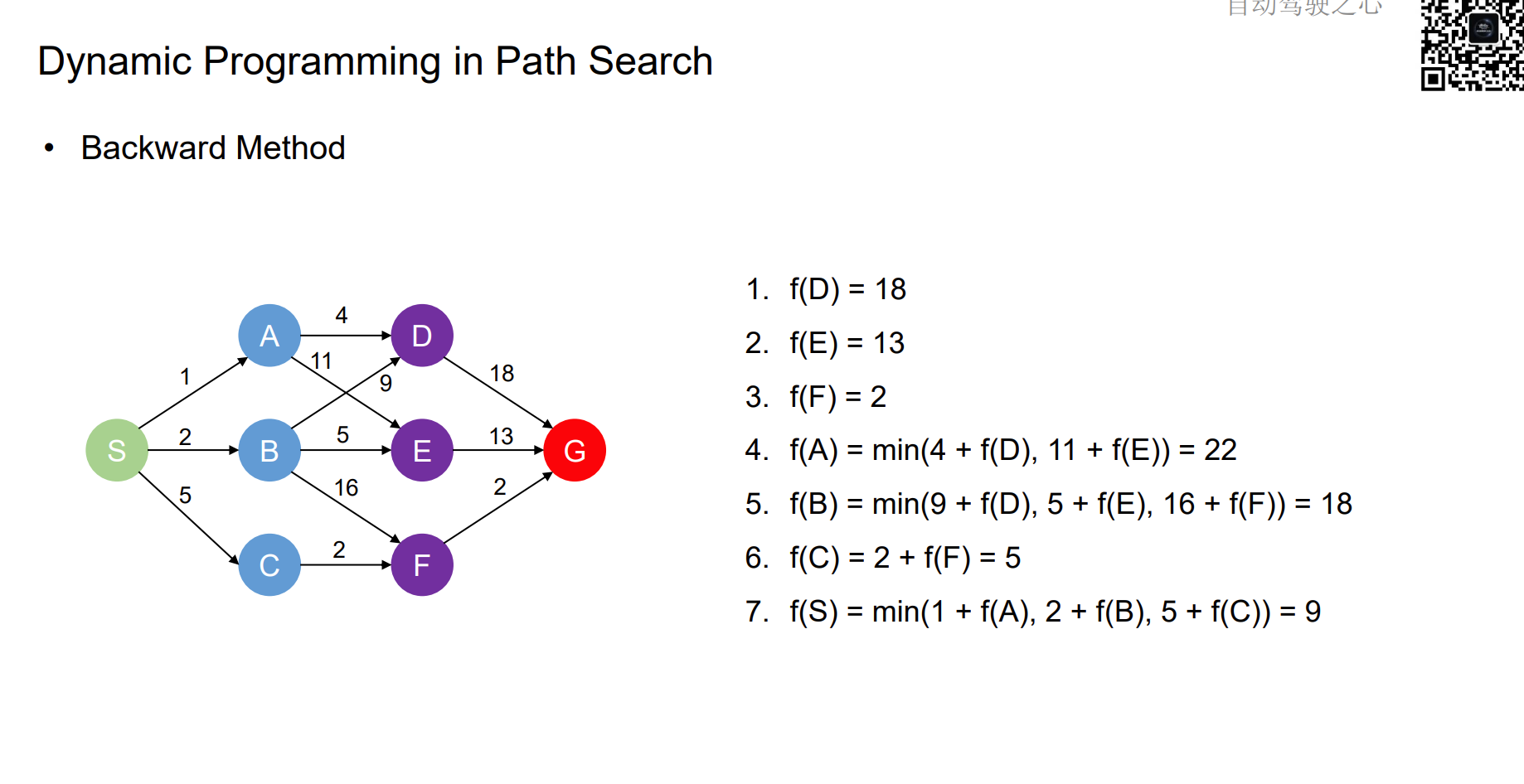
Sampling-based Planning Methods
General Recipe

Probabilistic Roadmap (PRM)
PRM
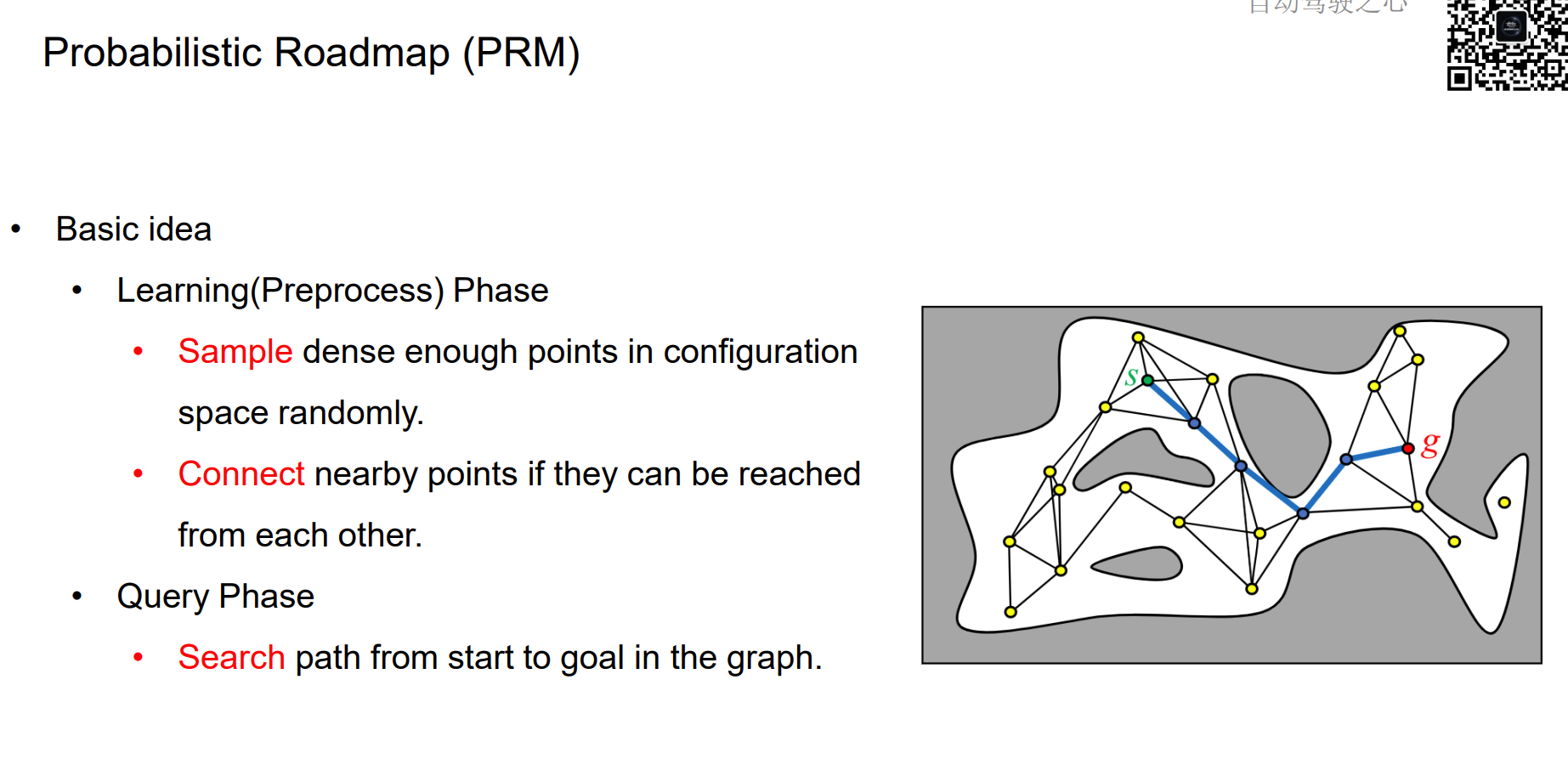
1、撒点来学习出图的结构,得到一个graph
2、用图搜索来搜索出最优的路径
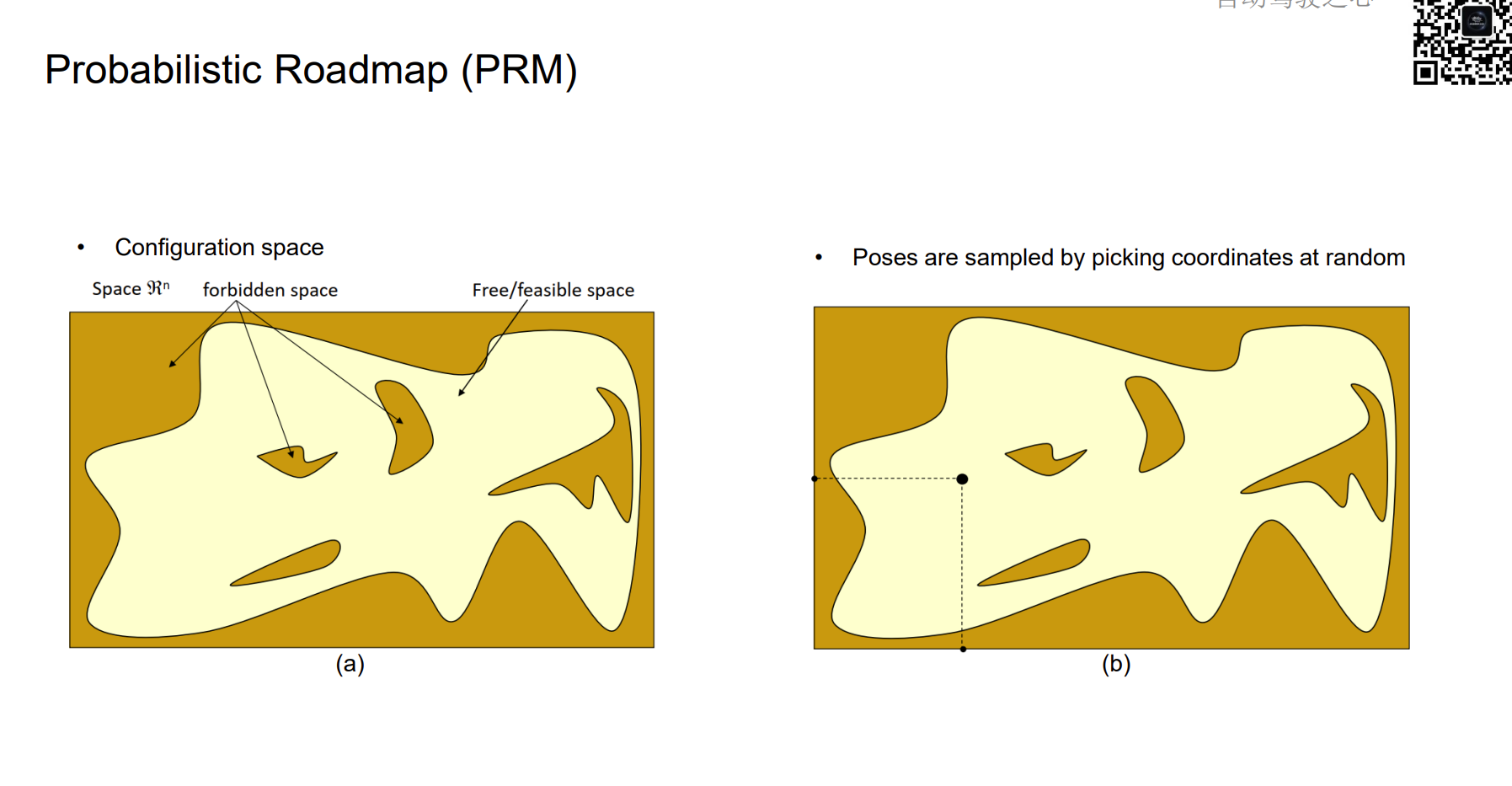
配置空间是指,在这样空间中规划的其实是一个质点,机器人的几何信息都被近似到forbidden space里面了。
对于图中的freespace来说,只要质点是在图中,那么可以忽略机器人几何形状的影响。
随机采样:依据某种分布,在一定范围内随
相关文章:

自动驾驶之心规划控制笔记
Search-based Path Planning Methods Path Finding Problem 一般来说指标有距离,耗费时间,能量,或者多目标。 左图是拓扑地图,蓝色的点就是顶点,绿色的线是连接关系。最后得到的是一个从哪里走的一个最优,并非精细解。 右图是栅格地图,这个搜索出来的是在相对分辨率比…...

Linux中部署Java jar 包 shell 脚本
Linux中部署Java jar 包 shell 脚本 #!/bin/bash set -e# 基础 # export JAVA_HOME/work/programs/jdk/jdk1.8.0_181 # export PATHPATH$PATH:$JAVA_HOME/bin # export CLASSPATH$JAVA_HOME/jre/lib/rt.jar:$JAVA_HOME/lib/dt.jar:$JAVA_HOME/lib/tools.jarDATE$(date %Y%m%d%…...
auto.js v1.4.4 实现自动打卡
一、使用场景 所在公司的打卡软件可以单独变成一个可以点击的APP,所以只需要实现以下步骤: 自动解锁屏幕返回主屏幕并打卡锁定屏幕需要的环境: 手机端下载并且安装 auto.js v4.1.1 PC端VS安装对应的插件学习资料 B站学习资料 对应 第三期&am…...

【Linux实验室】NFS、DHCP的搭建
NFS、DHCP的搭建 1、nfs服务搭建及测试什么是NFS?环境准备服务端机器安装nfs-utils和rpcbind包启动NFS服务创建/data/NFSdata目录,配置nfs文件启动服务挂载测试在服务端在共享目录下创建文件测试在客户端在共享目录下创建文件 2、dhcp服务搭建及测试什么…...
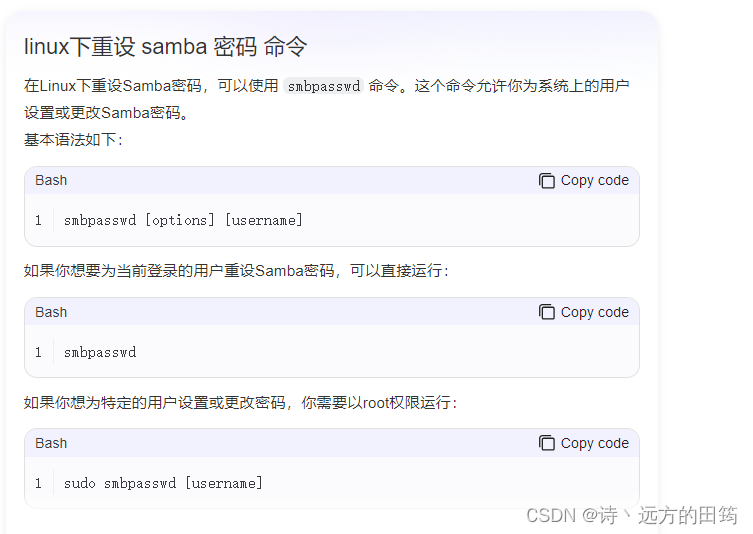
Samba 总是需要输入网络凭证
输入网络凭证: 用户名是 cat /etc/samba/smb.conf,查看 valid users mxw 为用户名。而不是其他账号名或者用户名,更不是登录计算机时的计算机名; 密码是 需要记住安装samba服务器时,自己设置的password࿱…...
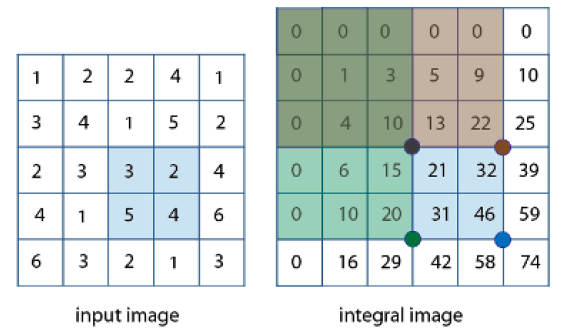
图像处理_积分图
目录 1. 积分图算法介绍 2. 基本原理 2.1 构建积分图 2.2 使用积分图 3. 举个例子 1. 积分图算法介绍 积分图算法是图像处理中的经典算法之一,由Crow在1984年首次提出,它是为了在多尺度透视投影中提高渲染速度。 积分图算法是一种快速计算图像区域和…...
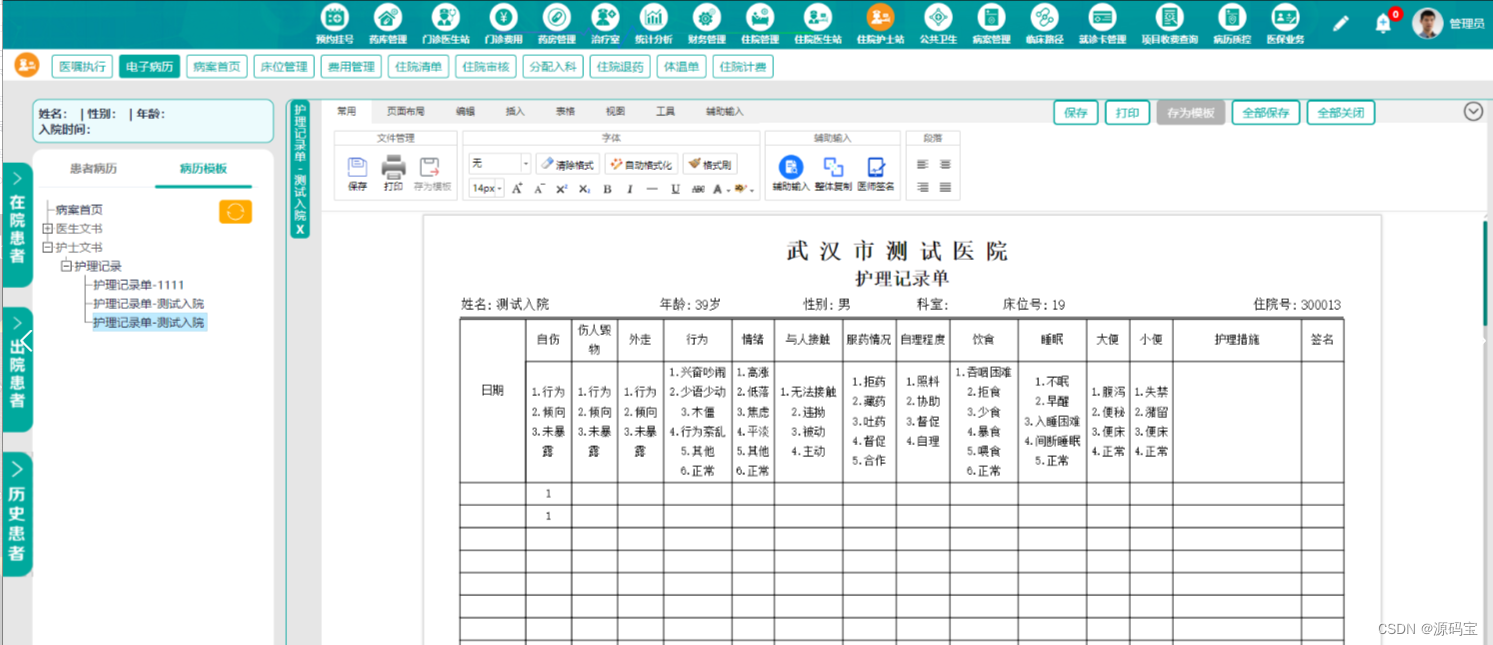
B/S架构SaaS模式 医院云HIS系统源码,自主研发,支持电子病历4级
B/S架构SaaS模式 医院云HIS系统源码,自主研发,支持电子病历4级 系统概述: 一款满足基层医院各类业务需要的云HIS系统。该系统能帮助基层医院完成日常各类业务,提供病患挂号支持、病患问诊、电子病历、开药发药、会员管理、统计查…...
1005 继续(3n+1)猜想)
(C)1005 继续(3n+1)猜想
1005 继续(3n1)猜想: 问题描述 卡拉兹(Callatz)猜想已经在1001中给出了描述。在这个题目里,情况稍微有些复杂。 当我们验证卡拉兹猜想的时候,为了避免重复计算,可以记录下递推过程中遇到的每一个数。例如对 n3 进行验证的时候&a…...
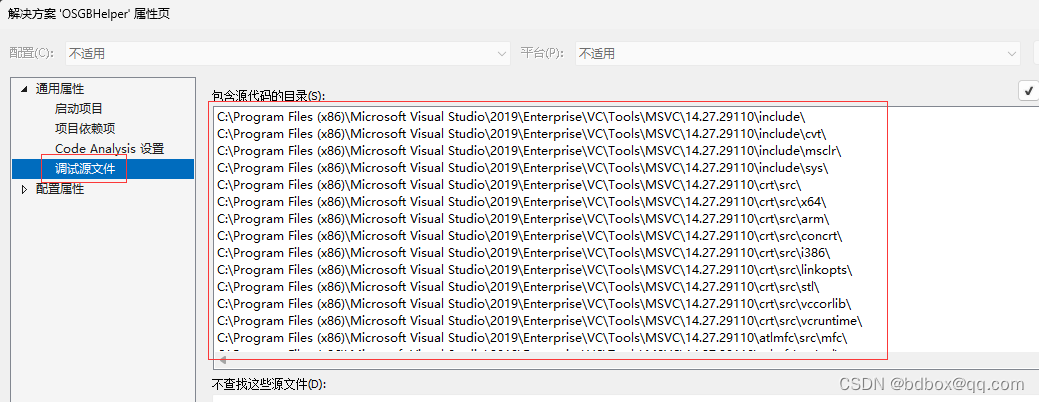
编译好的C++应用程序拷贝到其它电脑,提示dll未找到依赖项的解决方法。
编译好的C应用程序拷贝到其它电脑上,运行时出现提示dll未找到依赖项。 由于dll依赖于其它dll,在开发用电脑上的环境不能完全与其它电脑相同。 解决办法是找到调用到的dll依赖的所有dll,拷贝到运行目录下。 在开发电脑上: 1、开…...
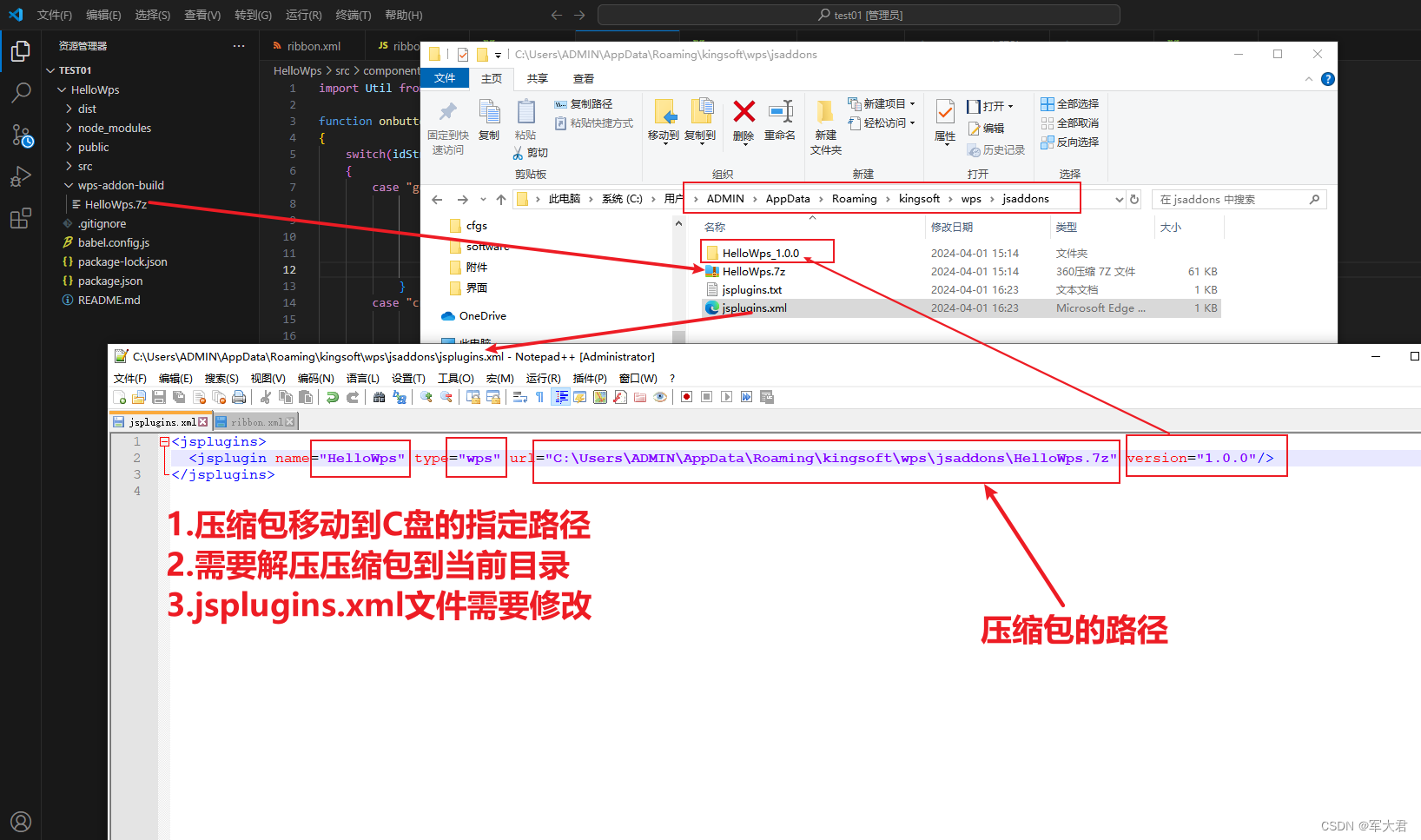
wps 开发插件
官方文档参考wps官方文档参考 1.环境安装 安装wps https://www.wps.cn/ 安装Node.js https://nodejs.org/en 安装代码编辑器 Visual Studio Code https://code.visualstudio.com/ 环境检查-进入cmd查看 node -v2.demo 2.1 demo下载 打开vscode,新建终端 安装…...

C语言----数据在内存中的存储
文章目录 前言1.整数在内存中的存储2.大小端字节序和字节序判断2.1 什么是大小端?2.2 练习 3.浮点数在内存中的存储3.1.引子3.2.浮点数的存储3.2.2 浮点数取的过程 前言 下面给大家介绍一下数据在内存中的存储,这个是一个了解c语言内部的知识点…...

【Linux学习】Linux 的虚拟化和容器化技术
˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如…...

Delphi 是一种内存安全的语言吗?
上个月,美国政府发布了 "回到基石 "报告: 通往安全和可衡量软件之路 "的报告。该报告是美国网络安全战略的一部分,重点关注多个领域,包括内存安全漏洞和质量指标。 许多在线杂志都对这份报告进行了评论࿰…...
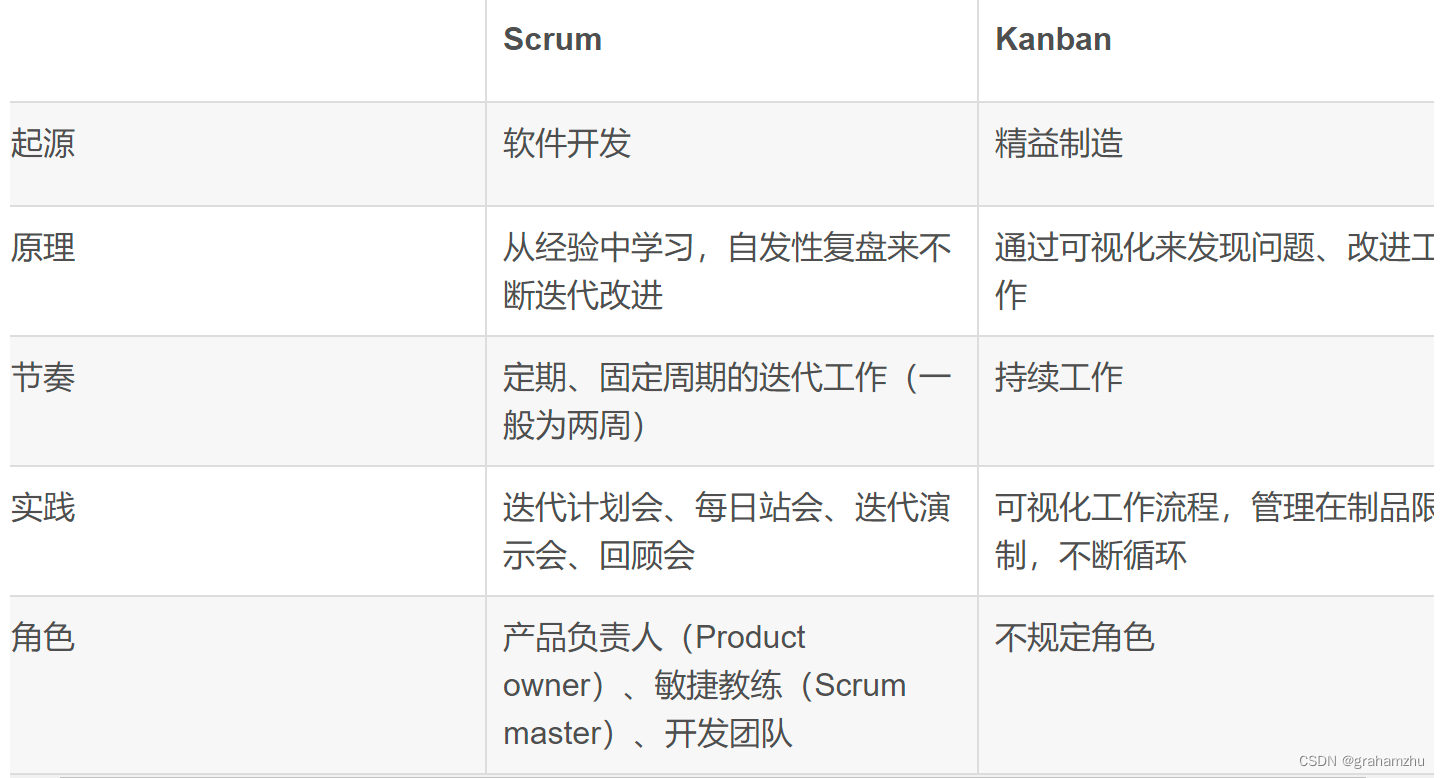
golang语言系列:Scrum、Kanban等敏捷管理策略
云原生学习路线导航页(持续更新中) 本文是 golang语言系列 文章,主要对编程通用技能 Scrum、Kanban等敏捷管理策略 进行学习 1.什么是敏捷开发 敏捷是一个描述软件开发方法的术语,它强调增量交付、团队协作、持续规划和持续学习。…...

QT背景介绍
🐌博主主页:🐌倔强的大蜗牛🐌 📚专栏分类:QT❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、QT背景 1.1什么是QT 1.2QT的发展历史 1.3什么是框架、库 1.4QT支持的平台 1.5QT的优点 1.6QT的…...
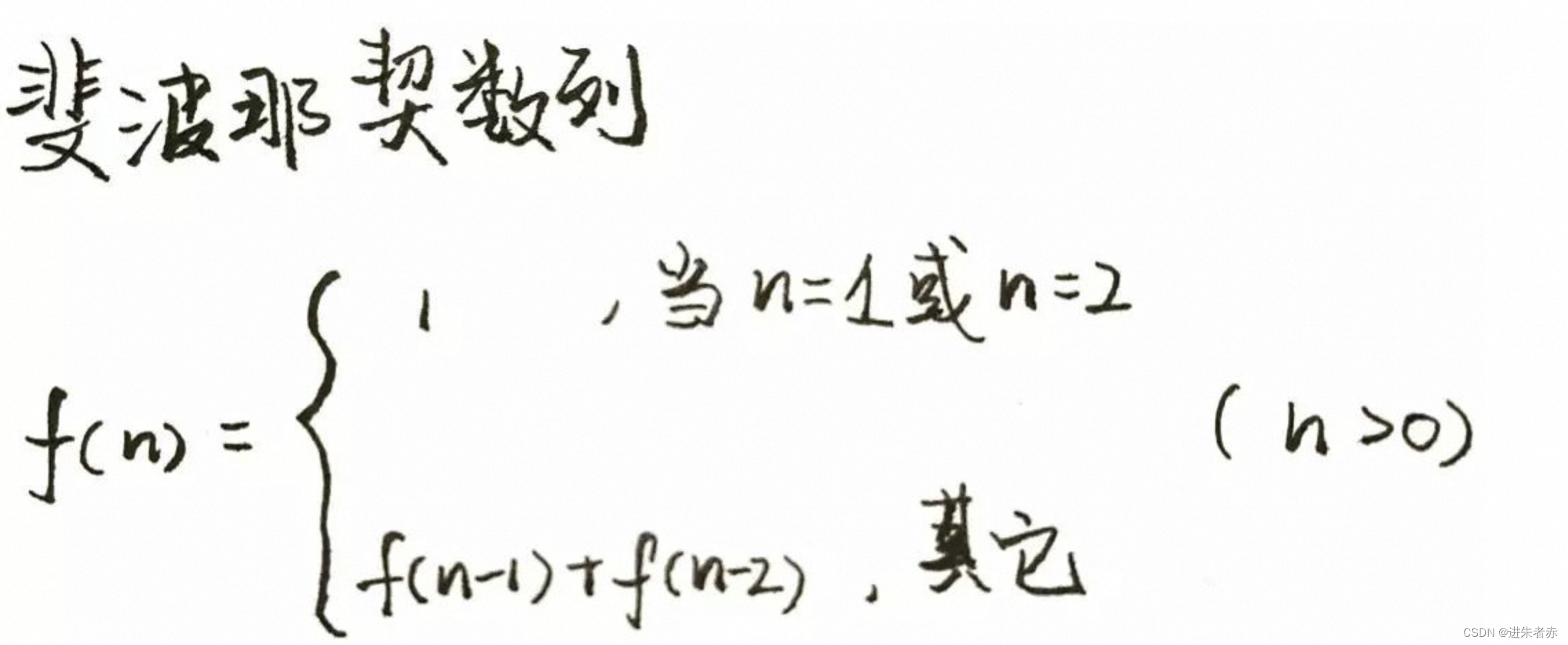
动态规划详解(Dynamic Programming)
目录 引入什么是动态规划?动态规划的特点解题办法解题套路框架举例说明斐波那契数列题目描述解题思路方式一:暴力求解思考 方式二:带备忘录的递归解法方式三:动态规划 推荐练手题目 引入 动态规划问题(Dynamic Progra…...

前端大额计算,真正解决js精度丢失问题
1.解决前端大额计算导致精度丢失问题 2.从底层上解决这个问题,计算时不使用js 运行时计算。 使用rust语言来解决这个问题,因为是底层语言,不涉及到精度问题。 3.实现步骤 步骤 1: 安装工具 确保你已经安装了Rust工具链和wasm-pack&#x…...
)
Android笔记--MediaCodec(一)
这一节主要来了解一下MediaCodec,Android MediaCodec 是 Android 平台提供的一个用于处理音频和视频数据的 API。它允许开发者对音频和视频数据进行编码和解码,支持多种格式和编解码器。MediaCodec API 通常用于实现实时音视频处理,如视频录制…...
Linux简单介绍
Linux简单介绍 编译器VMware虚拟机Ubuntu——LinuxOS为什么使用LinuxOS? 目录结构Windows目录结构Linux操作系统home是不是家目录? Linux常用命令终端命令行提示符与权限切换命令tab 作用:自动补全上下箭头pwd命令ls命令mkdir命令touch命令rm…...
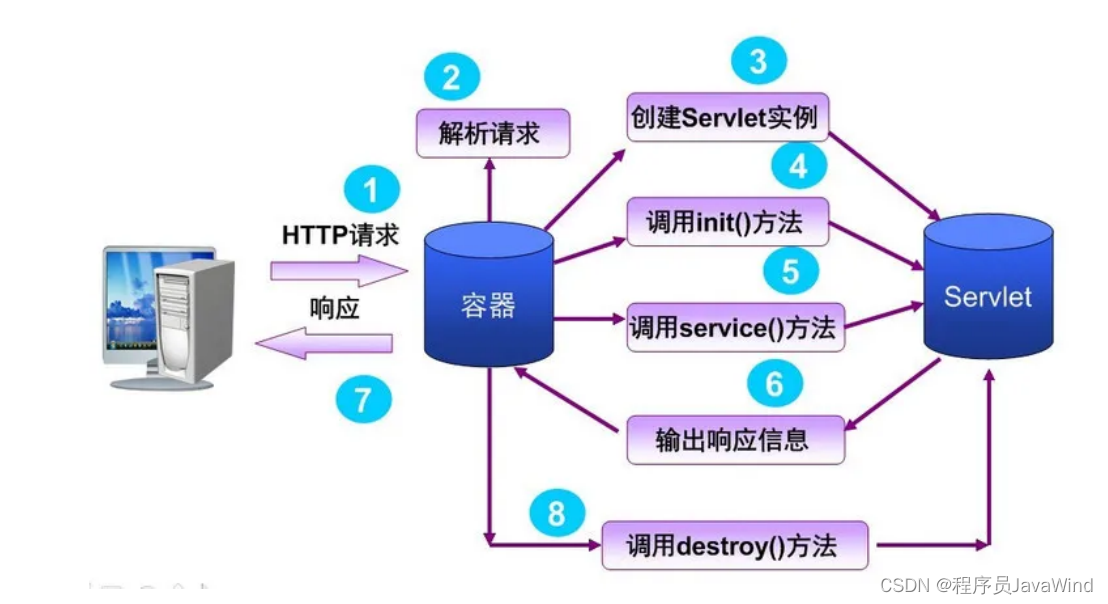
Servlet 的基本理解
Servlet 是JavaEE规范的一种,主要是为了扩展Java作为Web服务的功能,统一接口。由其他内部厂商如tomcat,jetty内部实现web的功能。如一个http请求到来:容器将请求封装为servlet中的HttpServletRequest对象,调用init()&a…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
