Stable Diffusion扩散模型【详解】小白也能看懂!!
文章目录
- 1、Diffusion的整体过程
- 2、加噪过程
- 2.1 加噪的具体细节
- 2.2 加噪过程的公式推导
- 3、去噪过程
- 3.1 图像概率分布
- 4、损失函数
- 5、 伪代码过程
此文涉及公式推导,需要参考这篇文章: Stable Diffusion扩散模型推导公式的基础知识
1、Diffusion的整体过程
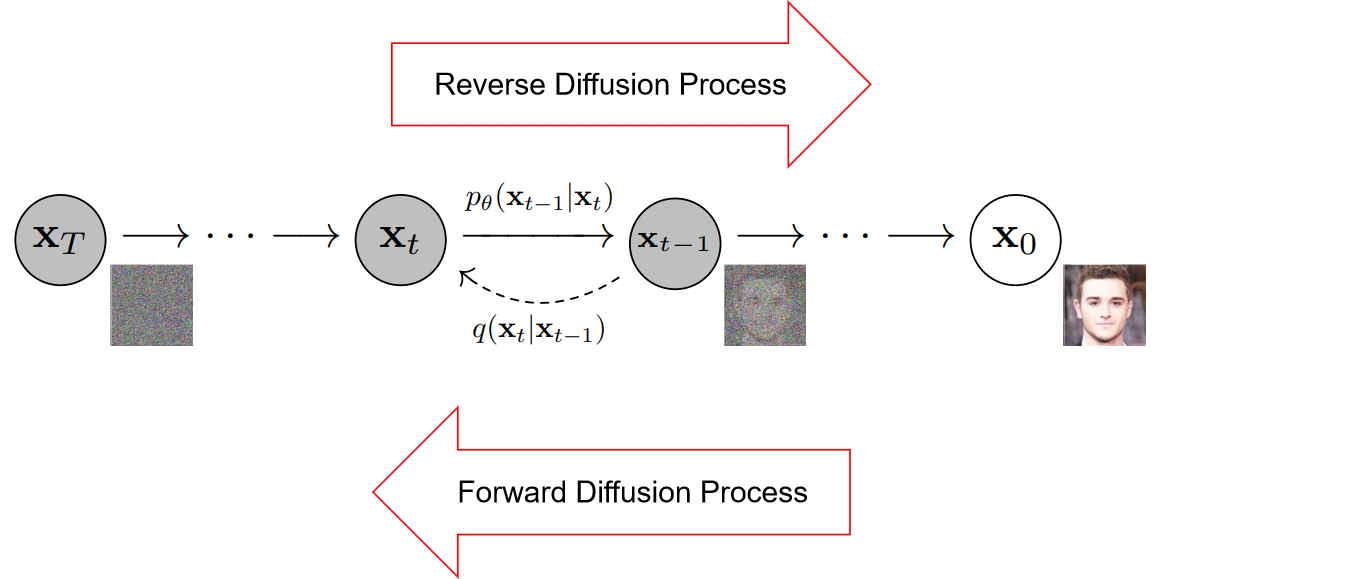
扩散过程是模拟图像加噪的逆向过程,也就是实现去噪的过程,
加噪是如下图从右到左的过程,称为反向扩散过程,
去噪是从左往右的过程,称为前向扩散过程,
2、加噪过程
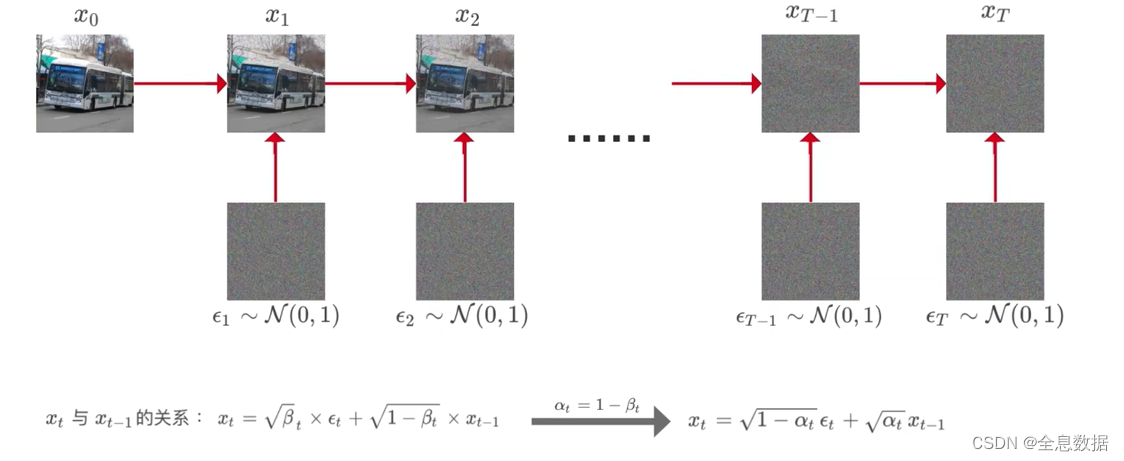
加噪过程如下图,下一时刻的图像是在上一时刻图像的基础上加入噪音生成的,
图中公式的含义: x t x_t xt表示 t 时刻的图像, ϵ t \epsilon_t ϵt 表示 t 时刻生成的随机分布的噪声图像, β t \beta_t βt表示 t 时刻指定的常数,不同时刻的 β t \beta_t βt不同,随着时间 t 的递增而增加,但需要注意 β t \beta_t βt的值始终是比较小的,因为要让图像的数值占较大的比例,
2.1 加噪的具体细节
A、将图像 x x x像素值映射到[-1,1]之间
图像加噪不是在原有图像上进行加噪的,而是通过把图片的每个像素的值转换为-1到1之间,比如像素的值是 x x x,则需要经过下面公式的处理 x 255 × 2 − 1 \frac{x}{255}\times2-1 255x×2−1,转换到范围是-1到1之间,
代码:
def get_transform():class RescaleChannels(object):def __call__(self, sample):return 2 * sample - 1return torchvision.transforms.Compose([torchvision.transforms.ToTensor(), RescaleChannels()])
B、生成一张尺寸相同的噪声图片,像素值服从标准正态分布
ϵ ∼ N ( 0 , 1 ) \epsilon \sim N(0,1) ϵ∼N(0,1)
x = {Tensor:(2, 3, 32, 32)}
noise = torch.randn_like(x)
C、 α \alpha α和 β \beta β
每个时刻的 β t \beta_t βt都各不相同,0 < β t \beta_t βt< 1,因为 β t \beta_t βt是作为权重存在的,且 β 1 < β 2 < β 3 < β T − 1 < β T \beta_1< \beta_2< \beta_3< \beta_{T-1}< \beta_T β1<β2<β3<βT−1<βT,
代码:
betas = generate_linear_schedule(args.num_timesteps,args.schedule_low * 1000 / args.num_timesteps,args.schedule_high * 1000 / args.num_timesteps)
β \beta β的取值代码,比如 β 1 \beta_1 β1取值low, β T \beta_T βT取值high,
# T:1000 Low/β1: 0.0001 high/βT: 0.02
def generate_linear_schedule(T, low, high):return np.linspace(low, high, T)
α t = 1 − β t \alpha_t=1-\beta_t αt=1−βt,alphas = 1.0 - betas
alphas = 1.0 - betas
alphas_cumprod = np.cumprod(alphas)
to_torch = partial(torch.tensor, dtype=torch.float32)
self.registerbuffer("betas", totorch(betas))
self.registerbuffer("alphas", totorch(alphas))
self.register_buffer("alphas_cumprod", to_torch(alphas_cumprod))
self.register_buffer("sqrt_alphas_cumpnod", to_torch(np.sqrt(alphas_cumprod)))
self.register_buffer("sart_one_minus_alphas_cumprod", to_torch(np.sqrt(1 - alphas_cumprod)))
self.registerbuffer("reciprocal sart_alphas", totorch(np.sart(1 / alphas)))
self.register_buffer("remove_noise_coeff", to_torch(betas / np.sqrt(1 - alphas_cumprod)))
self.registerbuffer("siqma",to_torch(np.sqrt(betas)))
D、任一时刻的图像 x t x_t xt都可以由原图像 x 0 x_0 x0直接生成(可以由含 x 0 x_0 x0的公式直接表示)
x t x_t xt与 x 0 x_0 x0的关系: x t = 1 − α t ‾ ϵ + α t ‾ x 0 x_t=\sqrt{1-\overline{\alpha_t}}\epsilon+\sqrt{\overline{\alpha_t}}x_0 xt=1−αtϵ+αtx0, α t = 1 − β t \alpha_t=1-\beta_t αt=1−βt, α t ‾ = α t α t − 1 . . . α 2 α 1 \overline{\alpha_t}=\alpha_t\alpha_{t-1}...\alpha_2\alpha_1 αt=αtαt−1...α2α1
由上式可知, β t \beta_t βt是常数,则 α t \alpha_t αt, 1 − α t ‾ \sqrt{1-\overline{\alpha_t}} 1−αt, α t ‾ \sqrt{\overline{\alpha_t}} αt也是常数, ϵ \epsilon ϵ也是已知的,所以可以直接由 x 0 x_0 x0生成 x t x_t xt,
def perturb_x(self, x, t, noise):return (extract(self.sqrt_alphas_cumprod, t, x.shape) * x +extract(self.sqrt_one_minus_alphas_cumprod, t, x.shape) * noise)
def extract(a, t, x_shape):b, *_ = t.shapeout = a.gather(-1, t)return out.reshape(b, *((1,) * (len(x_shape) - 1)))
2.2 加噪过程的公式推导
加噪过程:
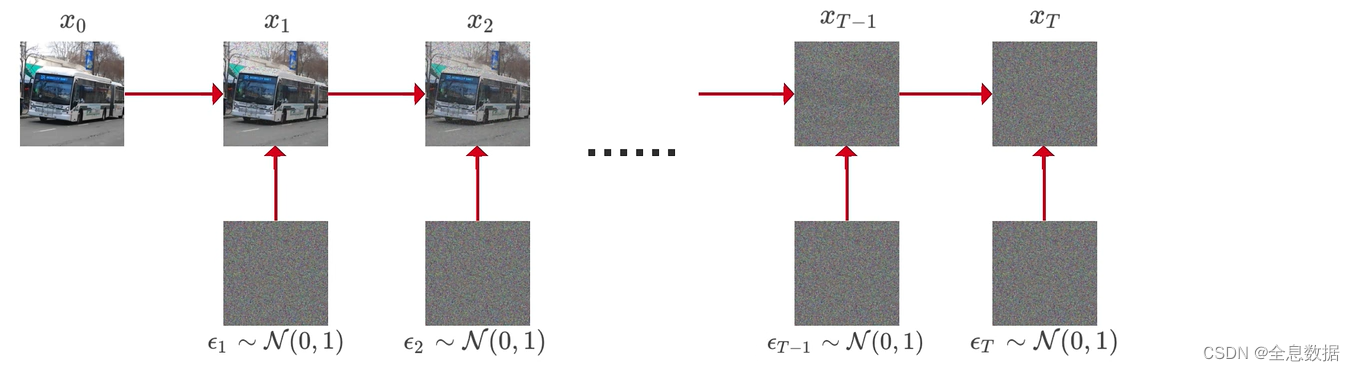
加噪过程的公式:




总结:

3、去噪过程
去噪是加噪的逆过程,由时间T时刻的图像逐渐去噪到时刻为0的图像,
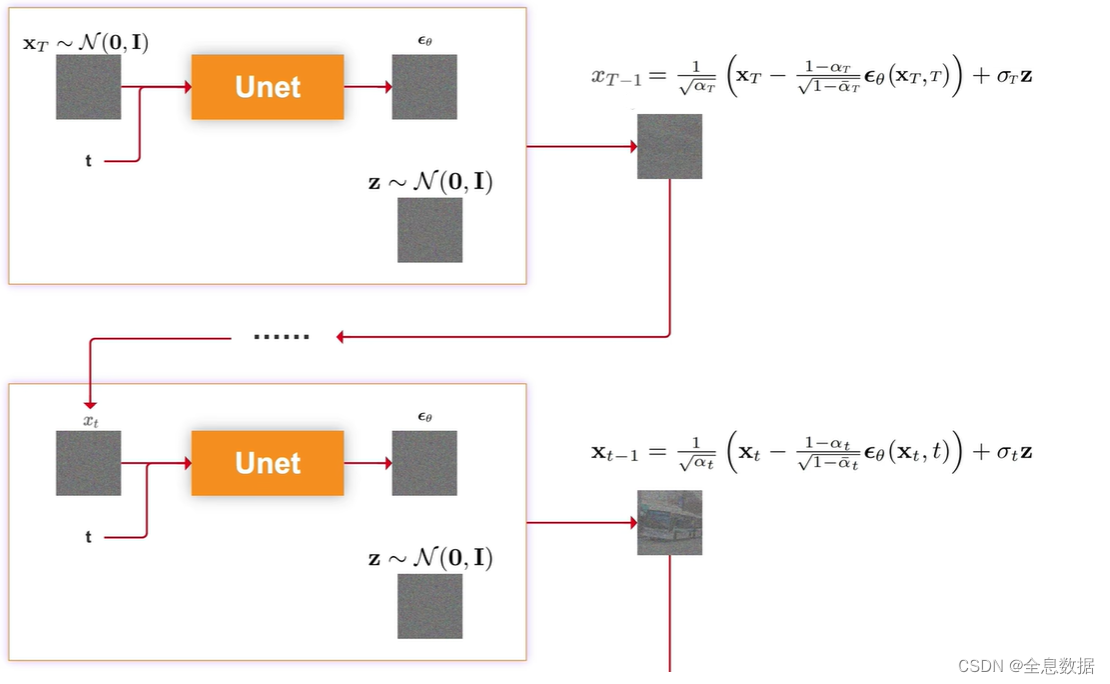
下面介绍一下由时刻为T的图像 x T x_T xT去噪到时刻为T-1的图像 x T − 1 x_{T-1} xT−1,输入为时刻为t的图像 x t x_t xt和时刻t,喂给Unet网络生成 ϵ θ \epsilon_\theta ϵθ,其中 θ \theta θ是Unet网络的所有参数,然后由下图中的 x t − 1 {\bf x}_{t-1} xt−1的公式即可生成时刻为t-1的图像 x t − 1 {\bf x}_{t-1} xt−1,
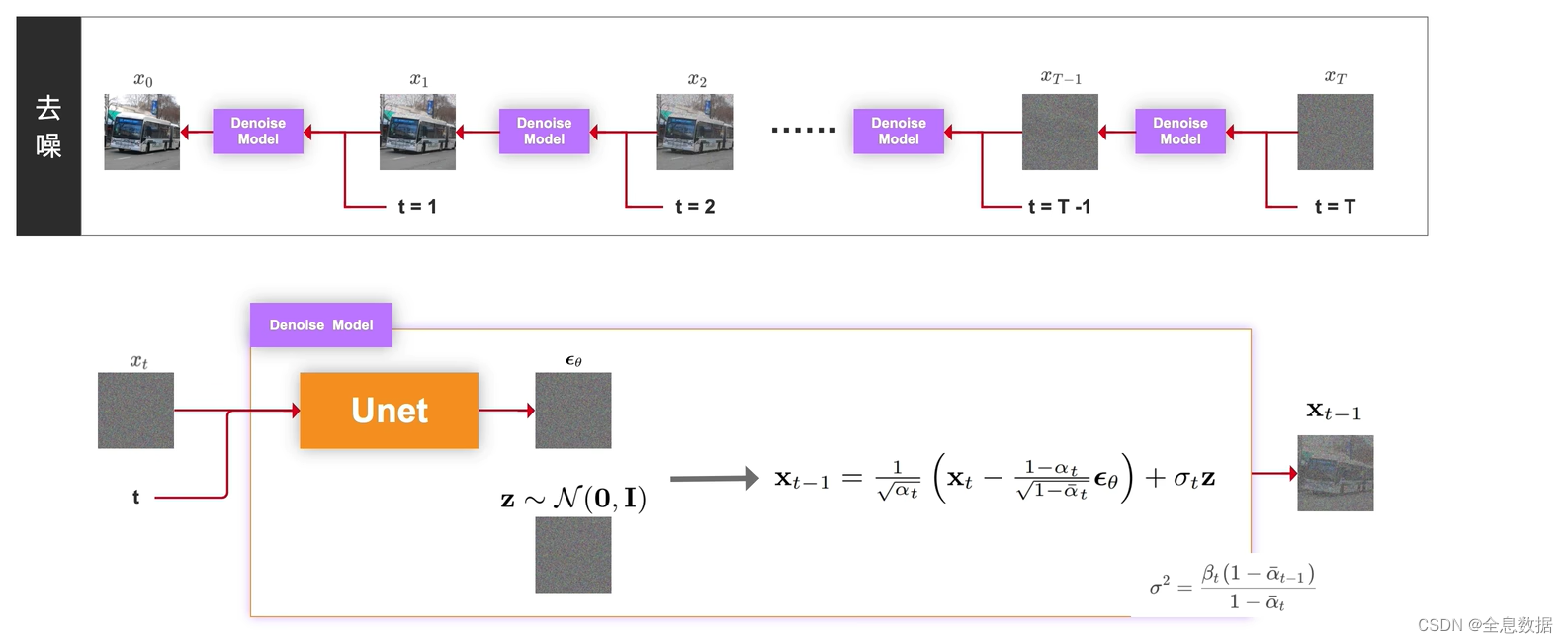
3.1 图像概率分布
去噪过程的2个假设:
(1)加噪过程看作马尔可夫链,假设去噪过程也是马尔可夫链,
(2)假设去噪过程是高斯分布,

假设数据集中有100张图片,每张图片的shape是4x4x3,假设每张图片的每个channel的每个像素点都服从正态分布, x t − 1 x_{t-1} xt−1的正态分布的均值 μ \mu μ 和方差 σ 2 \sigma^2 σ2 只和 x t x_t xt有关,已知在t时刻的图像,求t-1时刻的图像,

1、因为均值和方差 μ ( x t ) \mu(x_t) μ(xt), σ 2 ( x t ) \sigma^2(x_t) σ2(xt) 无法求出,所以我们决定让网络来帮我们预测均值和方差,
2、因为每一个像素都有自己的分布,都要预测出一个均值和方差,所以网络输出的尺寸需要和图像尺寸一致,所以我们选用 Unet 网络,
3、作者在论文中表示,方差并不会影响结果,所以网络只要预测均值就可以了,
4、损失函数

我们要求极大似然的最大值,需要对 μ \mu μ和 σ \sigma σ求导,但是对于扩散的过程是不可行的,如下面的公式无法求出,因为 x 1 : x T x_1:x_T x1:xT的不同组合所求出的 x 0 x_0 x0的值也不同,
p ( x 0 ) = ∫ x 1 : x T p ( x 0 ∣ x 1 : x T ) d x 1 : x T p(x_0)=\int_{x_1:x_T}p(x_0|x_1:x_T)d_{x_1:x_T} p(x0)=∫x1:xTp(x0∣x1:xT)dx1:xT
为了实现对极大似然函数的求导,把对极大似然求导的问题转换为ELBO :Evidence Lower Bound

对ELBO的公式继续进行化简,
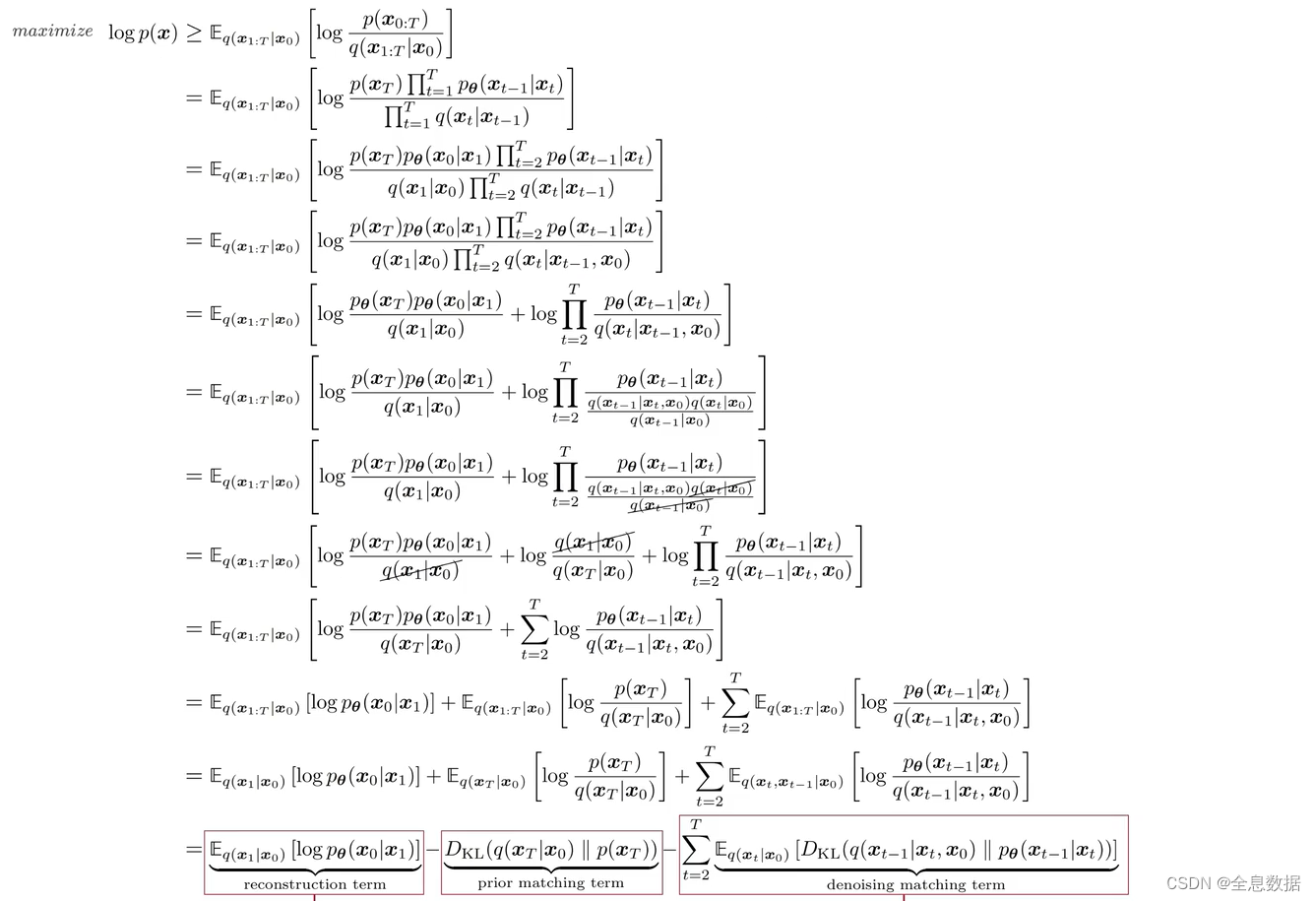

首先来看 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)表示已知 x 0 x_0 x0和 x t x_t xt的情况下推导 x t − 1 x_{t-1} xt−1,这个公式是可以求解的,如上图公式推导; p θ ( x t − 1 ∣ x t ) p_{\theta}(x_{t-1}|x_t) pθ(xt−1∣xt)需要使用 Unet 预测出该分布的均值,
q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)公式的推导如下:

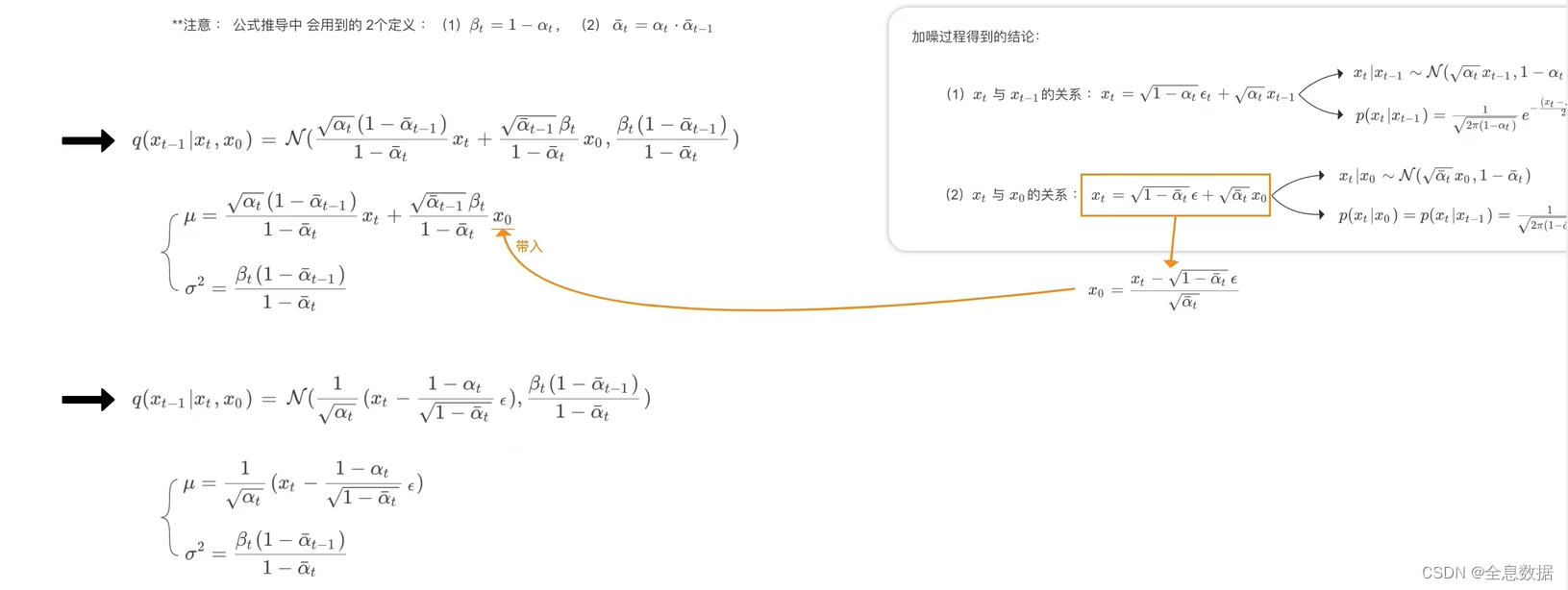
综上可知,UNet是在预测下面的公式,下面的公式中除了 ϵ \epsilon ϵ之外都是已知量,所以UNet网络实际预测的就是 ϵ \epsilon ϵ,
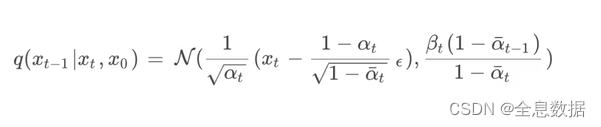
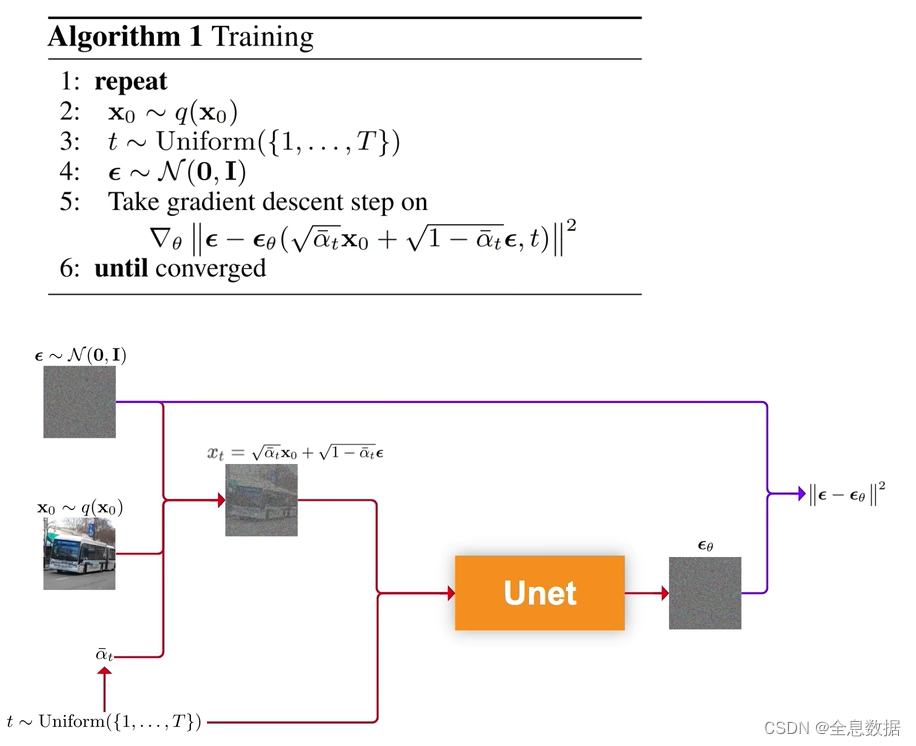
5、 伪代码过程
下图是训练阶段的伪代码,第1行和第6行表示第2行到第5行的代码一直在循环,
第2行:从数据集中筛选出一张图像,即为 x 0 \bf{x}_0 x0,
第3行:从0到 T T T的均匀分布中筛选出 t t t,源码中 T T T的范围设为1000,
第4行:从均值为0,方差为1的标准正态分布中采样出 ϵ \epsilon ϵ, ϵ \epsilon ϵ的size和 x 0 \bf{x}_0 x0的size是相同的,
第5行: x t x_t xt和从0到 T T T的均匀分布中筛选出 t t t喂给Unet,输出 ϵ θ \epsilon_\theta ϵθ,和第4行代码采样出的 ϵ \epsilon ϵ, ∣ ∣ ϵ − ϵ θ ( . . . ) ∣ ∣ 2 ||\epsilon-\epsilon_\theta(...)||^2 ∣∣ϵ−ϵθ(...)∣∣2的均方差作为损失函数,对这个损失函数求梯度进行参数更新,参数是Unet所有参数的集合 θ \theta θ,
下图是推导/采样/生成图片阶段的伪代码,
第1行:从随机分布中采样一个 x T {\bf x}_T xT,
第2行:遍历从 T T T到1,
第3行:从随机分布中采样一个 z \bf{z} z,
第4行:已知 z \bf{z} z、 α t \alpha_t αt、 σ t \sigma_t σt, ϵ θ \epsilon_\theta ϵθ是Unet网络生成的,就可以得到 x t − 1 {\bf x}_{t-1} xt−1
循环2-4行代码,

参考:
1、CSDN链接:链接
2、哔哩视频:https://www.bilibili.com/video/BV1ju4y1x7L4/?p=5&spm_id_from=pageDriver
3、论文Denoising Diffusion Probabilistic Models:https://arxiv.org/pdf/2006.11239.pdf
相关文章:

Stable Diffusion扩散模型【详解】小白也能看懂!!
文章目录 1、Diffusion的整体过程2、加噪过程2.1 加噪的具体细节2.2 加噪过程的公式推导 3、去噪过程3.1 图像概率分布 4、损失函数5、 伪代码过程 此文涉及公式推导,需要参考这篇文章: Stable Diffusion扩散模型推导公式的基础知识 1、Diffusion的整体…...

关于rabbitmq的prefetch机制
消息预取机制(Prefetch Mechanism)是RabbitMQ中用于控制消息传递给消费者的一种机制。它定义了在一个信道上,消费者允许的最大未确认的消息数量。一旦未确认的消息数量达到了设置的预取值,RabbitMQ就会停止向该消费者发送更多消息…...

机器学习介绍
机器学习是人工智能(AI)的一个分支,它使计算机系统能够从数据中学习并改进它们的性能。机器学习的核心在于开发算法,这些算法可以从大量数据中识别模式和特征,并用这些信息来做出预测或决策,而无需进行明确…...
OpenCV4.9开发之Window开发环境搭建
1.打开OpenCV所在github地址 2.点击opencv仓库,进入仓库详情,点击右下方的OpenCV 4.9.0进入下载页面 3.点击opencv-4.9.0-windows.exe下载 开始下载中... 下载完成 下载完成后,双击运行解压,默认解压路径,修改为c:/...

DDD 中的实体和值对象有什么区别?
在DDD中,实体 Entity 和值对象 Value Object 是两个基本的概念,它们之间有一些重要的区别。 唯一性:实体是唯一的,每个实体都有一个唯一的标识符,即使它的属性在一段时间内发生了变化,它仍然是这个实体。与…...

算法-最值问题
#include<iostream> using namespace std; int main() {int a[7];//上午上课时间int b[7];//下午上课时间int c[7];//一天总上课时间for (int i 0; i < 7; i) {cin >> a[i] >> b[i];c[i] a[i] b[i];}int max c[0];//max记录最长时间int index -1;//索…...

Go 性能压测工具之wrk介绍与使用
在项目正式上线之前,我们通常需要通过压测来评估当前系统能够支撑的请求量、排查可能存在的隐藏bug;压力测试(压测)是确保系统在高负载情况下仍能稳定运行的重要步骤。通过模拟高并发场景,可以评估系统的性能瓶颈、可靠…...
)
数学思想论(有目录)
数学思想是数学发展过程中的重要指导原则,它涉及对数学概念、方法和理论的理解和认识,以及如何利用这些工具来解决实际问题。数学思想的形成和演进是随着数学的发展而逐渐深化的,它体现了人类对数学本质和应用的不断探索和思考。 一些主要的数学思想包括: 函数与方程思想…...
C++的并发世界(五)——线程状态切换
0.线程状态 初始化:该线程正在被创建; 就绪:该线程在列表中就绪,等待CPU调度; 运行:该线程正在运行; 阻塞:该线程被阻塞挂机,Blocked状态包括:pendÿ…...
C语言——指针
地址是由物理的电线上产生的,能够标识唯一一个内存单元。在C语言中,地址也叫做指针。 在32位机器中,有32根地址线。地址是由32个0/1组成的二进制序列,也就是用4个字节来存储地址。 在64位机器中,有64根地址线。地址是…...

手搓二分查找
第一种: 该种方法是若a[mid]目标数,则让r一直等于mid,让l往右移动,一直移动到rl,这时候跳出循环,在循环外判断 但是不能写成让lmid,让r往左移动,比如a[2]key,这时&#x…...

pycharm调试(步过(Step Over)、单步执行(Step Into)、步入(Step Into)、步出(Step Out))
pycharm调试 pycharm调试 pycharm调试为什么要学会调试?1. 步过 (Step Over)2. 单步执行 (Step Into)3. 步入(Step Into)4. 步出(Step Out) 为什么要学会调试? 调试可以帮助初学者更深入地理解编程基础&am…...
Linux是什么,该如何学习
🐇明明跟你说过:个人主页 🏅个人专栏:《Linux :从菜鸟到飞鸟的逆袭》 🏅 🔖行路有良友,便是天堂🔖 目录 一、引言 1、Linux的起源与发展 2、Linux在现代计算机领域…...

C++ | Leetcode C++题解之第7题整数反转
题目: 题解: class Solution { public:int reverse(int x) {int rev 0;while (x ! 0) {if (rev < INT_MIN / 10 || rev > INT_MAX / 10) {return 0;}int digit x % 10;x / 10;rev rev * 10 digit;}return rev;} };...
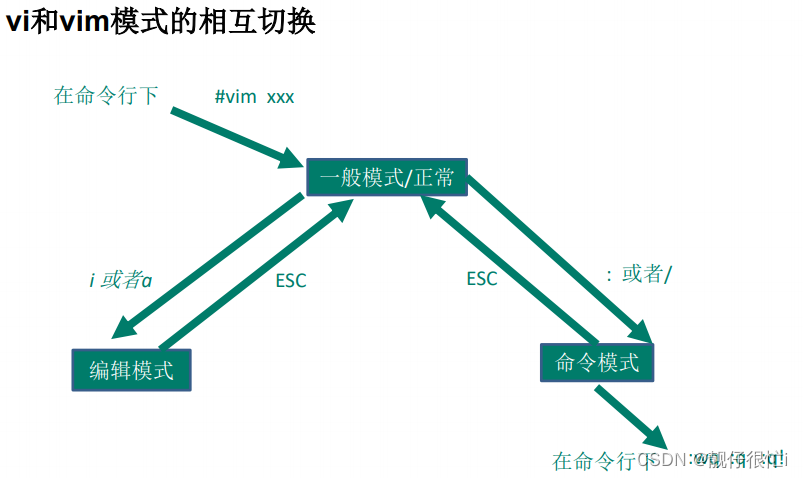
Linux------一篇博客了解Linux最常用的指令
🎈个人主页:靓仔很忙i 💻B 站主页:👉B站👈 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:Linux 🤝希望本文对您有所裨益,如有不足之处&#…...
vscode安装通义灵码
作为vscode的插件,直接使用 通义灵码-灵动指间,快码加编,你的智能编码助手 通义灵码,是一款基于通义大模型的智能编码辅助工具,提供行级/函数级实时续写、自然语言生成代码、单元测试生成、代码注释生成、代码解释、研…...
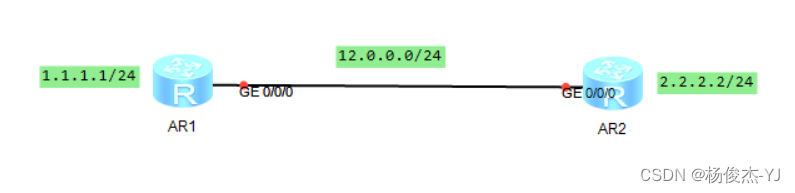
RIP协议(路由信息协议)
一、RIP协议概述 RIP协议(Routing Information Protocol,路由信息协议)是一种基于距离矢量的内部网关协议,即根据跳数来度量路由开销,进行路由选择。 相比于其它路由协议(如OSPF、ISIS等)&#…...

SpringBoot根据配置类动态加载不同环境下的自定义配置
dev环境配置 Profile({"dev","test"}) PropertySource("classpath:dev.properties") public class DevConfigLoader { }Profile("prod") PropertySource("classpath:prod.properties") public class ProdConfigLoader { }P…...
什么?穷哥们没钱RLHF?跟我一起DPO吧,丐版一样用
本次DPO训练采用TRL的方式来进行训练 Huggingface TRL是一个基于peft的库,它可以让RL步骤变得更灵活、简单,你可以使用这个算法finetune一个模型去生成积极的评论、减少毒性等等。 本次进行DPO的模型是一个500M的GPT-2,目的是训练快&#x…...
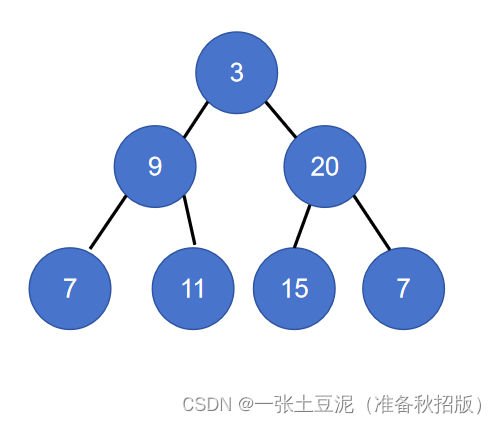
【Leetcode笔记】102.二叉树的层序遍历
目录 知识点Leetcode代码:ACM模式代码: 知识点 vector、queue容器的操作 对vector<int> vec;做插入元素操作:vec.push_back(x)。对queue<TreeNode*> que;做插入元素操作:que.push(root);。队列有四个常用的操作&…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

大模型真的像人一样“思考”和“理解”吗?
Yann LeCun 新研究的核心探讨:大语言模型(LLM)的“理解”和“思考”方式与人类认知的根本差异。 核心问题:大模型真的像人一样“思考”和“理解”吗? 人类的思考方式: 你的大脑是个超级整理师。面对海量信…...
