算法系列--递归,回溯,剪枝的综合应用(2)
💕"对相爱的人来说,对方的心意,才是最好的房子。"💕
作者:Lvzi
文章主要内容:算法系列–递归,回溯,剪枝的综合应用(2)
大家好,今天为大家带来的是
算法系列--递归,回溯,剪枝的综合应用(2)
一.括号⽣成
题目链接
括号生成
题目描述
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且有效的括号组合。
示例:
-
输入:n = 3
输出:[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”] -
输入:n = 1
输出:[“()”]
提示:
- 1 <= n <= 8
分析:

代码:
class Solution {List<String> ret;// 返回值StringBuffer path;// 记录搜索路径int maxLevel, lcnt, rcnt;// max表示最大层数 lcnt表示左括号的数量 rcnt表示右括号的数量public List<String> generateParenthesis(int n) {ret = new ArrayList<>();path = new StringBuffer();if (n == 0) return ret;maxLevel = 2 * n;dfs(1, lcnt, rcnt,n);return ret;}private void dfs(int level, int lcnt, int rcnt,int n) {// 递归出口if(level > maxLevel) {ret.add(path.toString());return;}if(lcnt < n) {path.append("(");dfs(level + 1,lcnt+1, rcnt,n);path.deleteCharAt(path.length() - 1);// 回溯}if(rcnt < n && lcnt > rcnt) {path.append(")");dfs(level + 1, lcnt, rcnt+1,n);path.deleteCharAt(path.length() - 1);// 回溯}}
}
二.目标和
题目链接
目标和
题目描述
给你一个非负整数数组 nums 和一个整数 target。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个表达式:
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 "+2-1" 。
返回可以通过上述方法构造的、运算结果等于 target 的不同表达式的数目。
示例:
-
输入:
nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有5种方法让最终目标和为3。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3 -
输入:
nums = [1], target = 1
输出:1
提示:
- 1 <= nums.length <= 20
- 0 <= nums[i] <= 1000
- 0 <= sum(nums[i]) <= 1000
- -1000 <= target <= 1000
分析:
思路同子集相同,子集中我们的决策策略是选不选当前的数,本题采用+当前数/-当前数

代码:
class Solution {int path, ret, target;public int findTargetSumWays(int[] nums, int _target) {target = _target;dfs(nums,0);return ret;}private void dfs(int[] nums, int pos) {if(pos == nums.length) {if(path == target) ret += 1;return;}// +path += nums[pos];dfs(nums,pos + 1);path -= nums[pos];//回溯// -path -= nums[pos];dfs(nums,pos + 1);path += nums[pos];// 回溯}
}
本题的最优解法其实是动态规划,具体可见我的这篇文章
算法系列–动态规划–背包问题(2)–01背包拓展题目
(有限制条件下的组合问题,且一个数只能选择一次–01背包问题)
3.组合总和
题目链接
组合总和
题目描述
给你一个无重复元素的整数数组 candidates 和一个目标整数 target,找出 candidates 中可以使数字和为目标数 target 的所有不同组合,并以列表形式返回。你可以按任意顺序返回这些组合。
candidates 中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例:
-
输入:
candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。 -
输入:
candidates = [2,3,5], target = 8
输出:[[2,2,2,2],[2,3,3],[3,5]] -
输入:
candidates = [2], target = 1
输出:[]
提示:
- 1 <= candidates.length <= 30
- 2 <= candidates[i] <= 40
- candidates 的所有元素互不相同
- 1 <= target <= 40
分析:
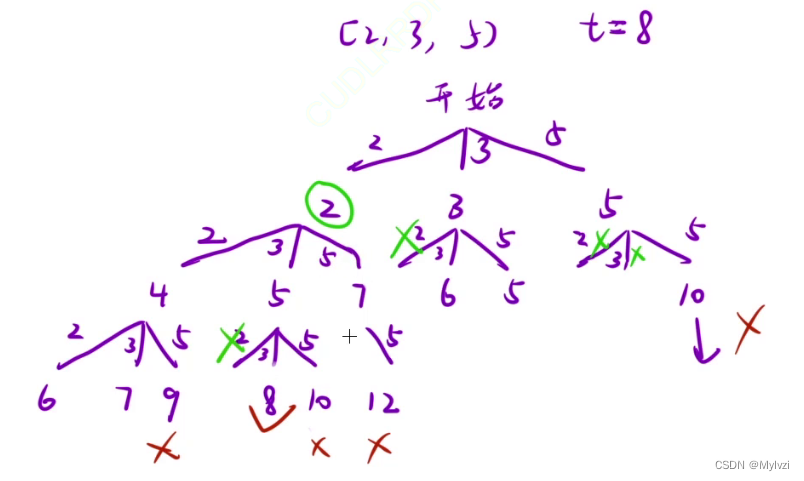
(如果本题是要求组合总和的最多组合数就是一个完全背包问题)
代码:
class Solution {List<List<Integer>> ret;List<Integer> path;// 保存搜索路径int sum, target;// sum记录搜索路径上的和public List<List<Integer>> combinationSum(int[] nums, int _target) {ret = new ArrayList<>();path = new ArrayList<>();target = _target;dfs(nums,0);return ret;}private void dfs(int[] nums, int pos) {if(sum >= target) {// 递归出口if(sum == target) {ret.add(new ArrayList<>(path));}return;}for(int i = pos; i < nums.length; i++) {path.add(nums[i]); sum += nums[i];dfs(nums,i);// 递归path.remove(path.size() - 1); sum -= nums[i];// 回溯}}
}
4.字⺟⼤⼩写全排列
题目链接
字⺟⼤⼩写全排列
题目描述
784. 字母大小写全排列
给定一个字符串 s,通过将字符串 s 中的每个字母转变大小写,我们可以获得一个新的字符串。
返回所有可能得到的字符串集合。以任意顺序返回输出。
示例:
-
输入:s = “a1b2”
输出:[“a1b2”, “a1B2”, “A1b2”, “A1B2”] -
输入: s = “3z4”
输出: [“3z4”,“3Z4”]
提示:
- 1 <= s.length <= 12
s由小写英文字母、大写英文字母和数字组成
解题思路
这道题可以使用回溯算法来解决。我们可以逐个遍历字符串中的每个字符,然后对于每个字符有两种选择:保持原大小写或者转换大小写。通过递归实现所有可能的组合。
代码实现(Java)
class Solution {List<String> ret;StringBuffer path;public List<String> letterCasePermutation(String s) {ret = new ArrayList<>();path = new StringBuffer();dfs(s,0);return ret;}private void dfs(String s, int pos) {if(pos == s.length()) {ret.add(path.toString());return;}// 不改变char ch = s.charAt(pos);path.append(ch);dfs(s, pos + 1);path.deleteCharAt(path.length() - 1);// 改变(非数字字符)if(ch < '0' || ch > '9') {char tmp = change(ch);path.append(tmp);dfs(s, pos + 1);path.deleteCharAt(path.length() - 1);}}private char change(char ch) {if(ch >= 'a' && ch <= 'z') return ch -= 32;else return ch += 32;}
}
5.优美的排列
题目链接
优美的排列
题目描述
526. 优美的排列
假设有从 1 到 n 的 n 个整数。用这些整数构造一个数组 perm(下标从 1 开始),只要满足下述条件之一,该数组就是一个优美的排列:
- perm[i] 能够被 i 整除
- i 能够被 perm[i] 整除
给你一个整数 n ,返回可以构造的优美排列的数量。
示例:
输入:n = 2
输出:2
解释:
- 第 1 个优美的排列是 [1,2]:
- perm[1] = 1 能被 i = 1 整除
- perm[2] = 2 能被 i = 2 整除
- 第 2 个优美的排列是 [2,1]:
- perm[1] = 2 能被 i = 1 整除
- i = 2 能被 perm[2] = 1 整除
解题思路
这道题可以使用回溯算法来解决。我们可以尝试将数字填充到数组的每个位置上,同时检查当前位置是否满足条件。如果满足条件,继续递归处理下一个位置;否则,回溯到上一个位置重新尝试其他数字。
check[i]:用于标记数字是否被使用过ret:返回值
代码实现(Java)
class Solution {int ret;// 返回值boolean[] check;// 用于标记已经使用过的数字public int countArrangement(int n) {check = new boolean[n + 1];dfs(1,n);return ret;}private void dfs(int pos, int n) {// pos是下标if(pos == n + 1) {// 递归出口ret += 1;return;}for(int i = 1; i <= n; i++) {if(check[i] == false && (pos % i == 0 || i % pos == 0)) {check[i] = true;// 将使用过的数字标记dfs(pos + 1, n);// 递归下一个位置check[i] = false;// 回溯}}}
}
在这段代码中:
pos表示当前递归到的位置,也就是在填充数组时当前正在考虑的位置。i则表示尝试填充到当前位置pos上的数字。
具体来说:
pos从1开始,代表数组中的位置,递归函数会尝试将数字填充到这些位置上。i从1到n,代表可以填充到当前位置的数字,即数组中的元素。
6. 组合
题目链接
组合
题目描述
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按任何顺序返回答案。
示例 1:
输入:n = 4, k = 2
输出:
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4],
]
示例 2:
输入:n = 1, k = 1
输出:[[1]]
提示:
- 1 <= n <= 20
- 1 <= k <= n
分析:
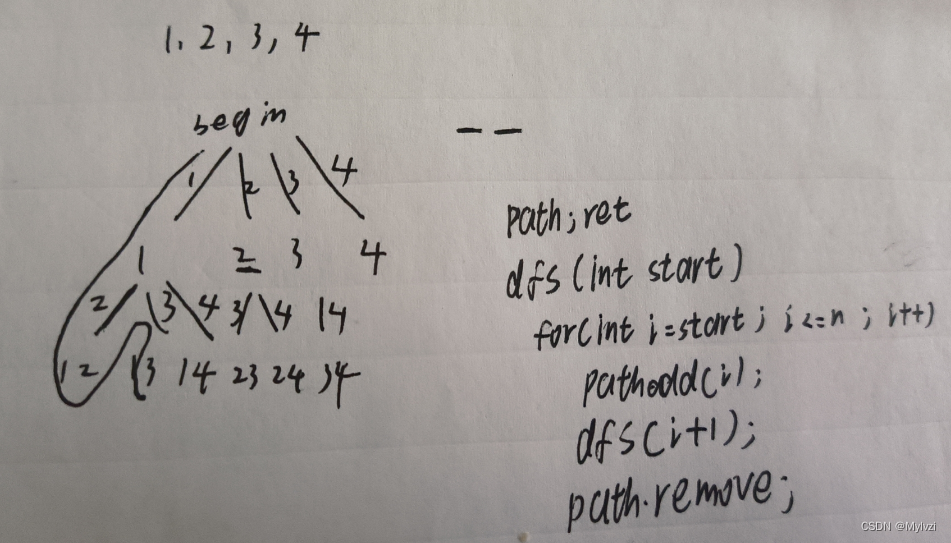
代码:
class Solution {List<List<Integer>> ret;List<Integer> path;int k, n;public List<List<Integer>> combine(int nn, int kk) {n = nn; k = kk;ret = new ArrayList<>();path = new ArrayList<>();dfs(1);return ret;}private void dfs(int start) {if(path.size() == k) {ret.add(new ArrayList<>(path));return;}for(int i = start; i <= n; i++) {path.add(i);// 添加当前数字dfs(i + 1);// 递归下一个数字path.remove(path.size() - 1);// 回溯}}
}
总结:
- 对于递归回溯这样的问题,一定要把决策树画的详细,要明确每一步的目的是什么,是根据什么进行递归的
对于这种递归回溯剪枝综合应用的题目来说,其分析思路是比较固定的:
- 画出详细的决策树(越详细越好,把所有的情况都写出来)
- 分析每一个子问题都是在干啥
- 设计全局变量和
dfs(其实dfs是这种问题最难的一步,dfs的设计本质上是一个递归的问题),dfs的设计包括三个方面:函数头,函数体,递归出口 - 考虑回溯和剪枝
相关文章:

算法系列--递归,回溯,剪枝的综合应用(2)
💕"对相爱的人来说,对方的心意,才是最好的房子。"💕 作者:Lvzi 文章主要内容:算法系列–递归,回溯,剪枝的综合应用(2) 大家好,今天为大家带来的是算法系列--递归,回溯,剪枝的综合应用(2) 一.括号…...

Docker搭建LNMP环境实战(09):安装mariadb
1、编写mariadb部署配置文件 在文件夹:/mnt/hgfs/dockers/test_site/compose下创建文件:test_site_mariadb.yml,内容如下: version: "3.5" services:test_site_mariadb:container_name: test_site_mariadbimage: mari…...
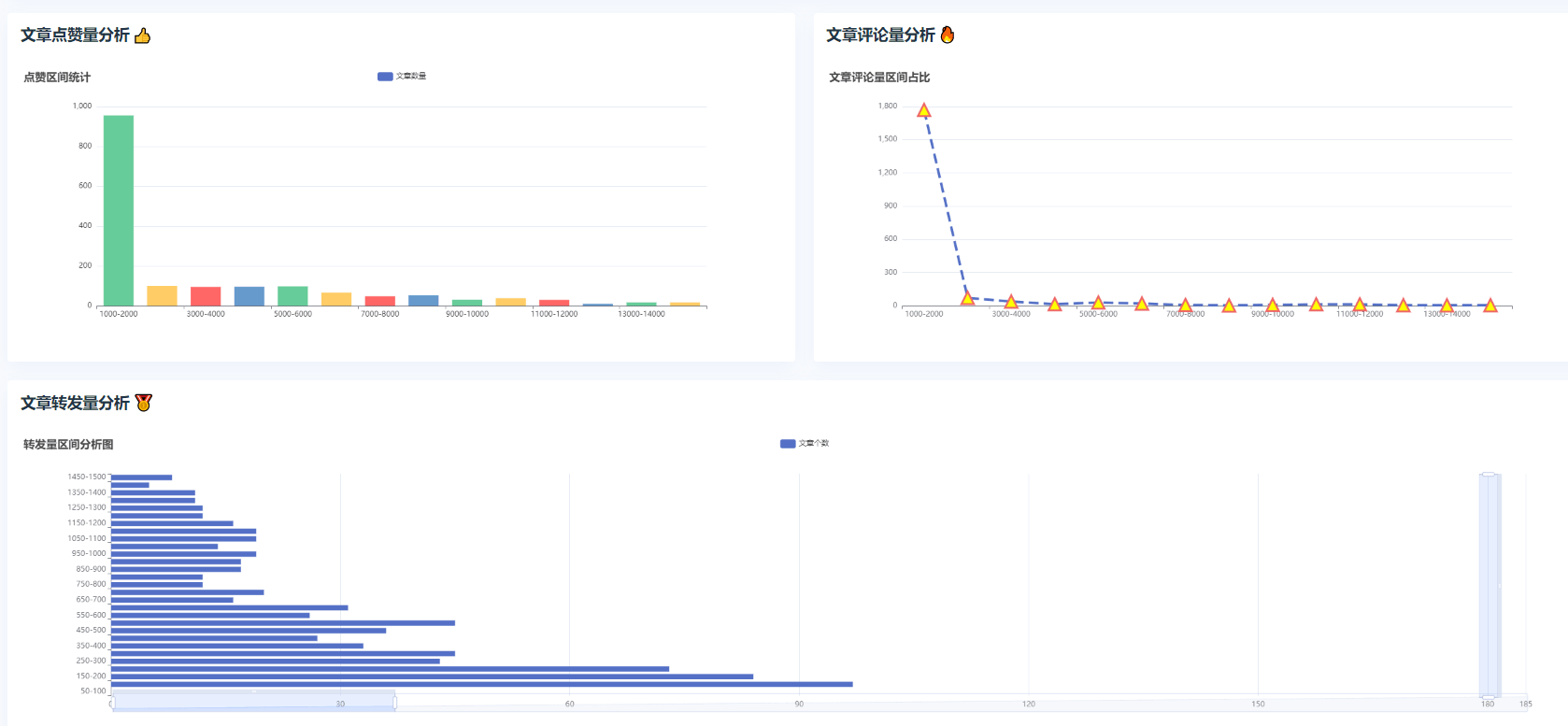
基于Python的微博舆论分析,微博评论情感分析可视化系统,附源码
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...
Flutter iOS上架指南
本文探讨了使用Flutter开发的iOS应用能否上架,以及上架的具体流程。苹果提供了App Store作为正式上架渠道,同时也有TestFlight供开发者进行内测。合规并通过审核后,Flutter应用可以顺利上架。但上架过程可能存在一些挑战,因此可能…...
实操:driver.js 实现产品导览、亮点、上下文帮助
官网 https://driverjs.com/ 依赖 <script src"https://cdn.jsdelivr.net/npm/driver.js1.0.1/dist/driver.js.iife.js"></script> <link rel"stylesheet" href"https://cdn.jsdelivr.net/npm/driver.js1.0.1/dist/driver.css"/…...

【JavaWeb】Day29.SpringBootWeb请求响应——请求(二)
请求响应 4.数组集合参数 数组集合参数的使用场景:在HTML的表单中,有一个表单项是支持多选的(复选框),可以提交选择的多个值。 4.1 数组 数组参数:请求参数名与形参数组名称相同且请求参数为多个,定义数组类型形参即…...
asf是什么格式的文件?用手机怎么打开?
由于手机操作系统和硬件的限制,大部分手机并不直接支持asf文件的播放。因此,如果你想在手机上打开asf文件,你可能需要先将文件转换为手机支持的格式,如MP4。可以通过使用一些视频转换软件来实现,比如野葱视频转换器。 …...
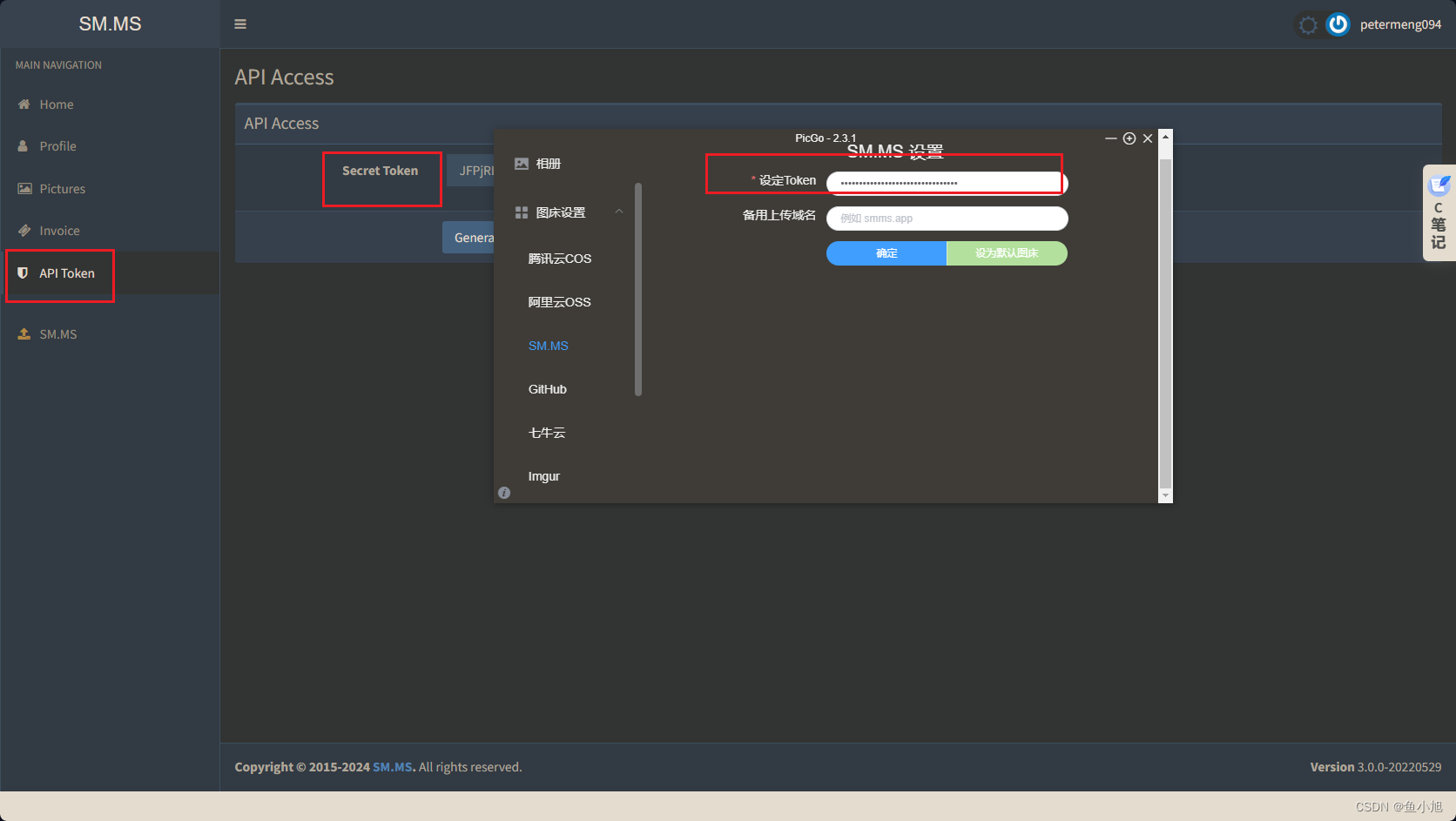
picGo图床搭建gitee和smms(建议使用)
picGoGitee 这个需要下载gitee插件, 因为官方频繁的检索文件类型, 有时候也会失效 如果没有特殊要求平时存个学习的要看图中文字的重要的图片建议就是smms, 免费也够用! 图片存本地不方便, 各种APP中来回传还会失帧损失画质, 所以你值得往下看 picGosmms 建议使用这个, sm…...
LeetCode | 数组 | 二分查找 | 35.搜索插入位置【C++】
题目链接 题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 示例 1: 输入: nums [1,3,5,6], target 5 输出…...

Linux 给网卡配置ip
ip addr | grep eth9 ifconfig eth9 10.0.0.2 netmask 255.255.255.0 up...

【C语言】翻译环境与运行环境
一、前言 在我们学习C语言的时候,第一个接触的程序就是:在屏幕上打印” hello word! “,可当时的我们却未去深入的理解与感悟,一个程序代码是如何运行的;而这一期的博客,则是带着我们,通过C代码…...

ubuntu20.04执行sudo apt-get update失败的解决方法
参考:执行sudo apt-get update失败的解决方案 1、换源型错误 (1)编辑/etc/apt/sources.list文件 在命令行中输入: sudo vim /etc/apt/sources.list 或者 sudo gedit /etc/apt/sources.list 推荐使用后者 (2…...
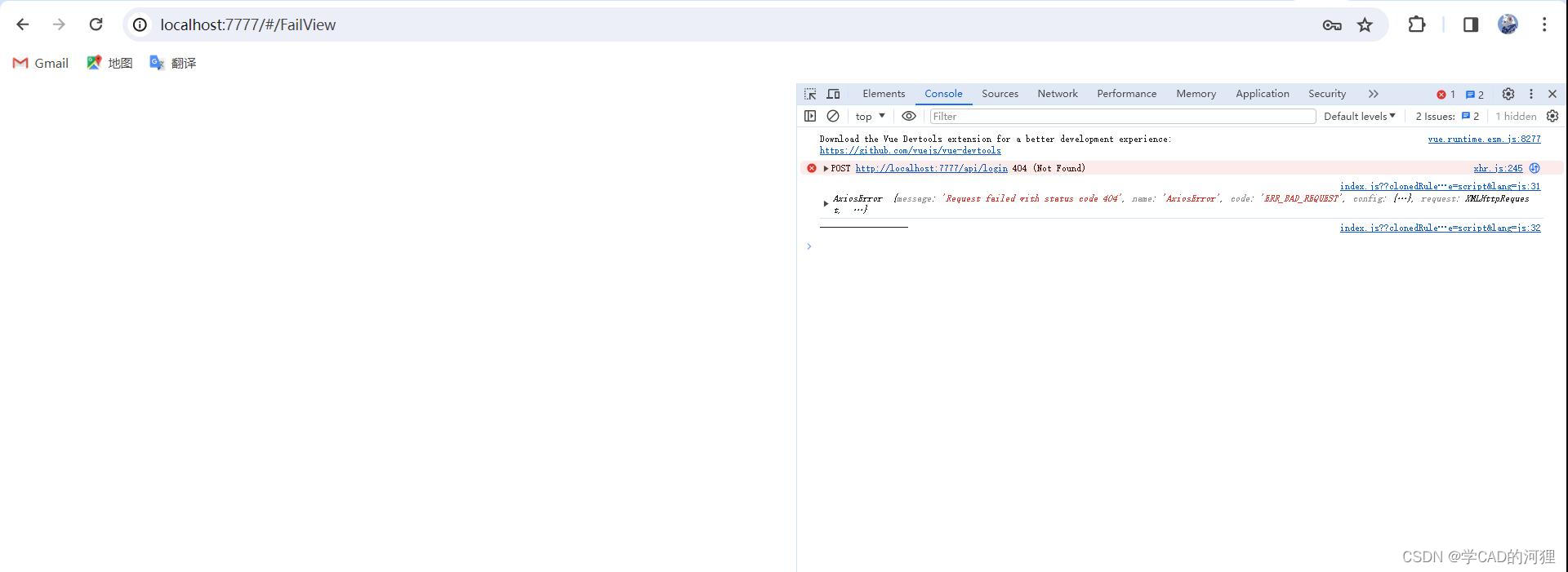
接口调用成功后端却一直返回404
vuespringboot 我在vue.config.js中配置了向后端的反向代理 然后使用了axios向后端发送post请求 可以看到可以接收到前端传来的值 但是前端控制台却报了 “xhr.js:245POST http://localhost:7777/api/login 404 (Not Found)” 最后询问我那智慧的堂哥... ... 解决办法是把C…...

【Vmware】 debian 12 安装教程
1.前提说明 VMware 17.5.1 (自行安装),参考Debian 12maven 3.8.7git 2.39.2jdk 1.8 / 11 / 17 1.1.Debian 下载 访问(https://www.debian.org/download) 下载 Debian 这是 Debian 12,代号为 bookworm,网络安装,用于 64 位 PC&a…...

YooAssets 使用相关
## 使用 YooAssets 动态加载原生文件时候 > 原生文件:txt;json;等需要直接保存文件内string字符的文件 需要将打包方式设置成为,PackRawFile 并且加载时候使用 API : YooAssets.LoadRawFileSync()YooAssets.LoadRa…...

精准扶贫管理系统|基于Springboot的精准扶贫管理系统设计与实现(源码+数据库+文档)
精准扶贫管理系统目录 目录 基于Springboot的精准扶贫管理系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、管理员模块的实现 (1)用户信息管理 (2)贫困户信息管理 (3)新闻类型管理 &a…...

Flutter与iOS和Android原生页面交互
一、Flutter 与原生页面交互的重要性和应用场景 Flutter 是一个由 Google 开发的开源框架,用于创建跨平台的移动、Web 和桌面应用程序。Flutter 允许开发者使用一套代码库为 Android 和 iOS 等平台构建美观、高性能的应用程序。然而,尽管 Flutter 提供了…...
Chrome安装Vue插件vue-devtools
直接通过网站: Home | Vue Devtools (vuejs.org) chrome扩展商城中搜索:Vue.js devtools 参考下面edge扩展商城的图,两者流程相近...

内存和网卡压力测试
1.内存压力测试 1.1测试目的 内存压力测试的目的是评估开发板中的内存子系统性能和稳定性,以确保它能够满足特定的应用需求。开发板通常用于嵌入式系统、物联网设备、嵌入式智能家居等场景,这些场景对内存的要求通常比较高。 其内存压力测试的主要目的…...

法律行业案例法模型出现,OPenAI公布与法律AI公司Harvey合作案例
Harvey与OpenAl合作,为法律专业人士构建了一个定制训练的案例法模型。该模型是具有复杂推理广泛领域知识以及超越单一模型调用能力的任务的AI系统,如起草法律文件、回答复杂诉讼场景问题以及识别数百份合同之间的重大差异。 Harvey公司由具有反垄断和证…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

