【算法每日一练]-数论(保姆级教程 篇1 埃氏筛,欧拉筛)
目录
保证给你讲透讲懂
第一种:埃氏筛法
第二种:欧拉筛法
题目:质数率
题目:不喜欢的数
思路:
问题:1~n 中筛选出所有素数(质数)
有两种经典的时间复杂度较低的筛法,即埃氏筛法和欧拉筛法。
既然是筛子,那么核心思想就是:根据当前的数筛掉后面的一些不合法数据,留下的每个数都是质数。
第一种:埃氏筛法
(也是最好理解的筛子,不过速度O(n*loglogn))
首先2是最小的素数,将表中所有的2的倍数划去。
表中剩下的最小的数字就是3,所以3是素数。再将表中所有的3的倍数划去……
以此类推,如果表中剩余的最小的数是几,几就是素数。然后将其倍数筛掉
核心代码:
第二个for为什么从i*i开始:
答:我们会先筛2的所有倍数,然后是3的倍数,但是后面在筛3的倍数的时候我们还需要从2开始筛吗?筛掉3*2?这个之前在筛2的时候就已经标记过了的,那么直接从3本身筛开始多好啊。
int eprime(int n){judge[0]=judge[1]=1;for(int i=2;i<=n;i++){if(judge[i]==0){prime[cnt++]=i;for(int j=i*i;j<=n;j+=i) judge[j]=1;//直接从i本身开始筛}}return cnt;
}重点: 虽然埃氏筛易理解,但是个别时候还是会被卡的。
我们深入理解埃氏筛的思想:
要想得到 n以内的质数,就要把不大于根号n的质数的倍数全部剔除,剩下的就是质数。从 2 开始,把 2 的倍数(不包括本身)标记为合数,然后向后枚举,查到一个未标记为合数的,就把它的倍数(不包括本身)标记为合数。以此类推,查到 n 为止。
例如一个数 24,它会被 2 标记一次,被3标记一次。如果这个数的质因数较多,那么重复的就会更多,每个已经被筛掉的数重复的被筛,这就会导致时间变长
(放心,欧拉来了)
第二种:欧拉筛法
欧拉筛法的原理同埃氏筛法,只不过多了一个判断删除与标记最小质因子的过程。
在埃氏筛法中,一个合数来说可能会被筛多次,比如6可以被2筛去,也可以被3筛去,而欧拉筛要做的事情就是让一个合数只被筛一次。
我们规定这个合数只会被它的最小质因数筛掉。这样能保证每个合数只会被筛一次。
核心代码
int oprime(int n){//线性筛O(n)速度求出小于n的所有质数!!!judge[0]=judge[1]=1;for(int i=2;i<=n;i++){if(!judge[i]) prime[cnt++]=i;//没有被标记过的数必然是质数,加入质数中for(int j=0;prime[j]*i<=n;j++){//质数性倍增(只枚举当然已放入的质数)judge[prime[j]*i]=true;//此数的质数倍数加入标记中if(i%prime[j]==0)break;//保证了一个合数只被它最小的质因子枚举标记,而一个质数只会一直枚举标记到本身}}return cnt;
}过程如下:
从 2开始:2 加入 prime 数组,从小到大枚举质数(现在只有 2),筛掉质数与 2 的乘积(4 被筛掉)。
到了 3: 3 加入 prime 数组,从小到大枚举质数(此时有 2,3),筛掉质数与 3 的乘积(6,9 被筛掉)。
到了 4: 4 没加入 prime 数组,枚举质数(有2,3),筛掉 8 后,因为 4mod2=0,触发退出条件。(不触发,就会筛掉 12,而 12=2×2×3,又会被 2 和 6筛一次,懂了吗)
以此类推,可做出一张表:
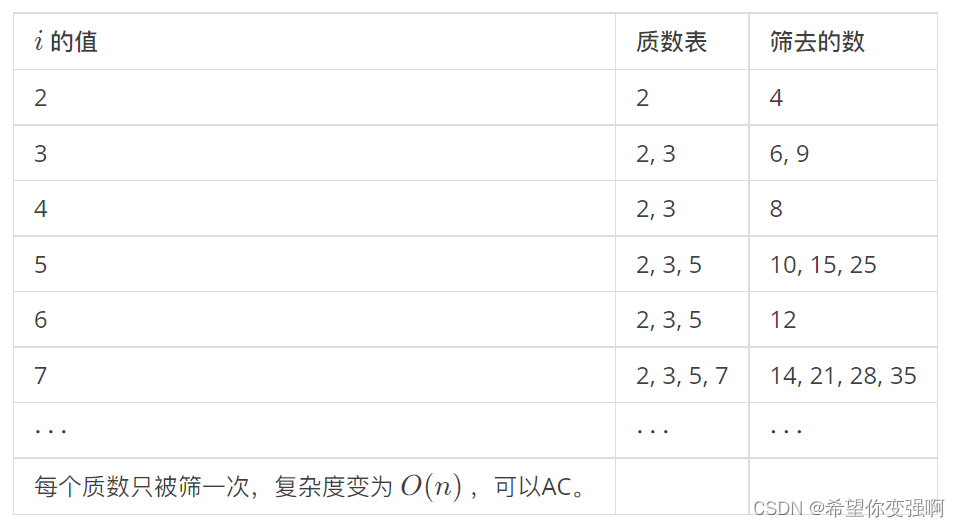
不难发现保证一个合数只被它最小的质因子枚举标记,而一个质数只会一直枚举标记到本身。保证了合数只被一次筛掉。
下面是完整代码:
#include <bits/stdc++.h>//线性筛模板
using namespace std;
bool judge[1000000];
int n,cnt,prime[1000];
int oprime(int n){//线性筛O(n)速度求出小于n的所有质数!!!judge[0]=judge[1]=1;for(int i=2;i<=n;i++){if(!judge[i]) prime[cnt++]=i;//没有被标记过的数加入质数中for(int j=0;prime[j]*i<=n;j++){//1,质数性倍增(只枚举当然已放入的质数)judge[prime[j]*i]=true;//此数的质数倍数加入标记中(必然不是质数)if(i%prime[j]==0)break;//2,保证一个合数只被它最小的质因子枚举标记,而一个质数只会一直枚举标记到本身}}return cnt;
}
int eprime(int n){judge[0]=judge[1]=1;for(int i=2;i<=n;i++){if(judge[i]==0){prime[cnt++]=i;for(int j=i*i;j<=n;j+=i) judge[j]=1;}}return cnt;
}
int main(){cin>>n;eprime(n);//oprime(n);for(int i=0;i<cnt;i++){cout<<prime[i]<<' ';}return 0;
}以上算法只有两步(已标出)和埃氏筛不同,注意一下即可
最终效果:zhi数组里面全是质数,vis数组里面为true的都不是质数,既方便取质数,又方便判断质数。
下面是练习题
题目:质数率
题意:求1~n的质数占比(n<=1e8)
(这道题还是很友好的,直接让你精确,而不是求逆元,哈哈哈哈哈)
#include <bits/stdc++.h>
using namespace std;
const int N=1e8+7;
int zhi[N],cnt,m;
bool vis[N];//千万不要用int来充当bool了,内存直接超256M了!!!
int getzhi(int n){for(int i=2;i<=n;i++){if(!vis[i])zhi[cnt++]=i; //如果你这里想用++cnt,那么后面的j应该从1开始for(int j=0;zhi[j]*i<=n;j++){vis[zhi[j]*i]=true;if(i%zhi[j]==0)break;}}return cnt;
}
int main(){cin>>m;getzhi(m);printf("%0.3lf\n",(double)cnt/m);
}
题目:不喜欢的数
我们不喜欢7的倍数;数字的某一位是7,这个数字的倍数我们也不喜欢。给t个数,如果这个数不是喜欢的数就输出下一个喜欢的数
思路:
注意到一个含7的数的倍数也不行,很明显我们倒着找的话需要找所有的因数来判断,但是t太大了,这样必然超时。只能正着来做!
线性筛思想O(n):如果此数喜欢,那就加入数组;否则就把此数的倍数全部筛掉
注意到要输出不喜欢数的下一个喜欢的数。对于这种取一个数的后一个数,那就定义一个链表呗(就是跟踪数组嘛)里面存放下标可以,直接存放那个数也可以,感觉你直接存那个数的话更好!
#include <bits/stdc++.h>
using namespace std;//如果是喜欢的数,就输出下一个喜欢的数(大于次数的下一个喜欢的数)(t<=2e5 x<=1e7)
const int N=1e7+7;
int t,x,ans[N],nxt[N],cnt;
bool judge[N]={1};
bool check(int x){while(x){if(x%10==7)return true;x/=10;}return false;
}
void getnum(int n){//线性筛思想int cur=1;//cur是上个喜欢的数,此时是第一个喜欢的数for(int i=2;i<=n;i++){if(!judge[i]){//忽略被筛掉的数bool f=check(i);if(!f){//喜欢ans[cnt++]=i;//放入数组,感觉此步骤有点多余nxt[cur]=i;//更新链表,里面存入这个数的下个数cur=i;//更新cur}else{for(int j=i;j<=n;j+=i)//线性倍增的结果都标记一下(都是不喜欢的数)judge[j]=true;}}}
}
int main(){getnum(N);//先对所有范围内的数都打下表格cin>>t;while(t--){cin>>x;if(judge[x]) cout<<-1<<'\n';//不喜欢则直接输出-1else cout<<nxt[x]<<'\n';//喜欢则输出这个数的下一个数}return 0;
}相关文章:

【算法每日一练]-数论(保姆级教程 篇1 埃氏筛,欧拉筛)
目录 保证给你讲透讲懂 第一种:埃氏筛法 第二种:欧拉筛法 题目:质数率 题目:不喜欢的数 思路: 问题:1~n 中筛选出所有素数(质数) 有两种经典的时间复杂度较低的筛法࿰…...

【剑指offr--C/C++】JZ59 滑动窗口的最大值
一、题目 二、思路及代码 暴力解法是依次往后滑动一位,然后比较窗口内的值。 我这里考虑:窗口每次往后移动一位,那么如果当前窗口的最大值max在窗口内部,那么再滑动到下一个窗口的时候,窗口内只有最新进来的一个元素没…...

RabbitMQ Tutorial
参考API : Overview (RabbitMQ Java Client 5.20.0 API) 参考文档: RabbitMQ: One broker to queue them all | RabbitMQ 目录 结构 Hello World consumer producer 创建连接API解析 创建连接工厂 生产者生产消息 消费者消费消息 队列声明 工作队列Work Queues 公平…...
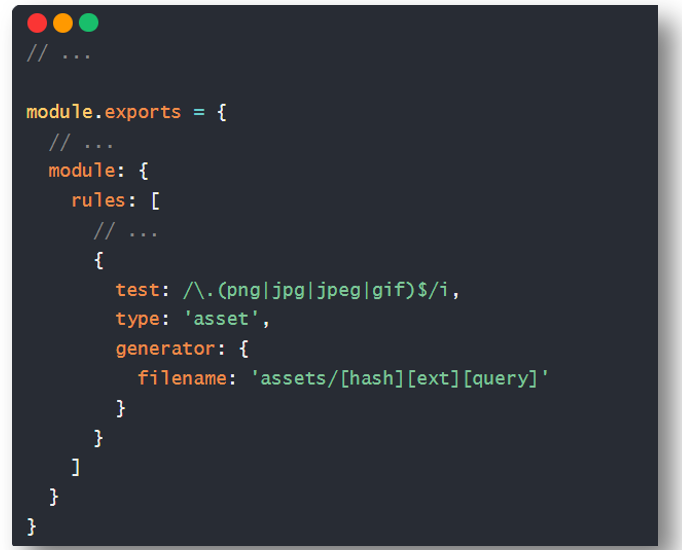
如何对Webpack进行优化
目录 1.优化-提取css代码 1.1. 插件 mini-css-extract-plugin 1.2. 步骤: 1.3. 注意 1.4. 好处 1.5. 练习 2. 优化-css代码提取后压缩 2.1. 问题引入 2.2. 解决 2.3. 步骤 3. Webpack打包less代码 3.1. 加载器 less-loader 3.2. 步骤 3.3. 注意…...
nut-ui中的menu 菜单组件的二次封装
这个菜单组件 一般可以直接用到项目里 如果复用性不强的话 直接使用 但是有一个问题 如果很多地方都需要用到这个组件 我们可以把这个组件二次封装一下 <template><div class"cinema-search-filter-component"><nut-menu><template #icon>&…...
序列)
python笔记(11)序列
Python中的“序列”是一个广义术语,用于描述一种特定的数据结构,它具备以下共同特征: 有序性:序列中的元素按照特定的顺序排列,每个元素在序列中都有一个确定的位置,即索引。 索引访问:通过索引…...
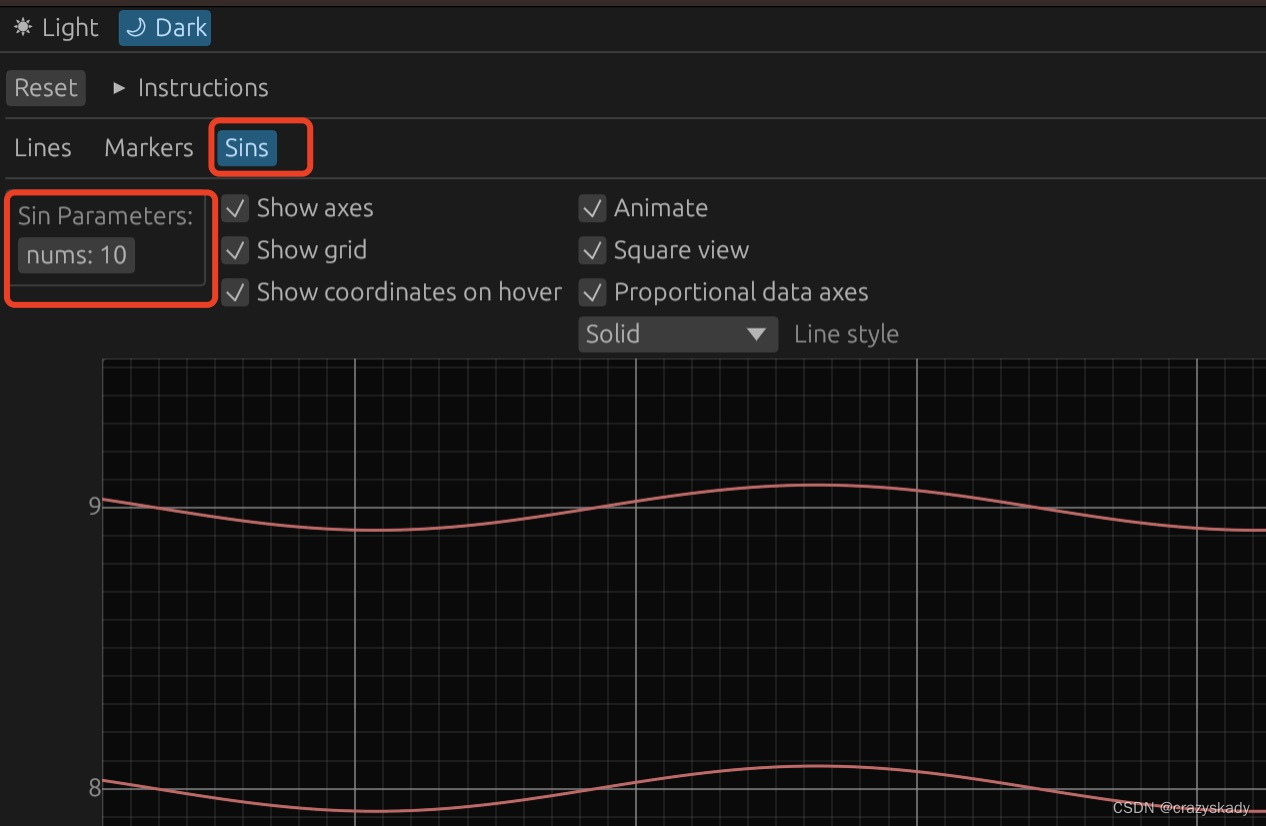
Rust egui(4) 增加自己的tab页面
如下图,增加一个Sins也面,里面添加一个配置组为Sin Paraemters,里面包含一个nums的参数,范围是1-1024,根据nums的数量,在Panel中画sin函数的line。 demo见:https://crazyskady.github.io/index.…...

小组分享第二部分:Jsoup
1.Jsoup是什么: 是HTML的解析器,可以解析URL地址,HTML的文本内容,可以使用DOM,CSS以及类似Jquery的操作方法来操作数据 2.Jsoup的作用 1.通过URL或者文件或者字符串获取到HTML页面并解析 2.使用DOM或CSS等操作来对数据进行操作 3.可以操作HT…...
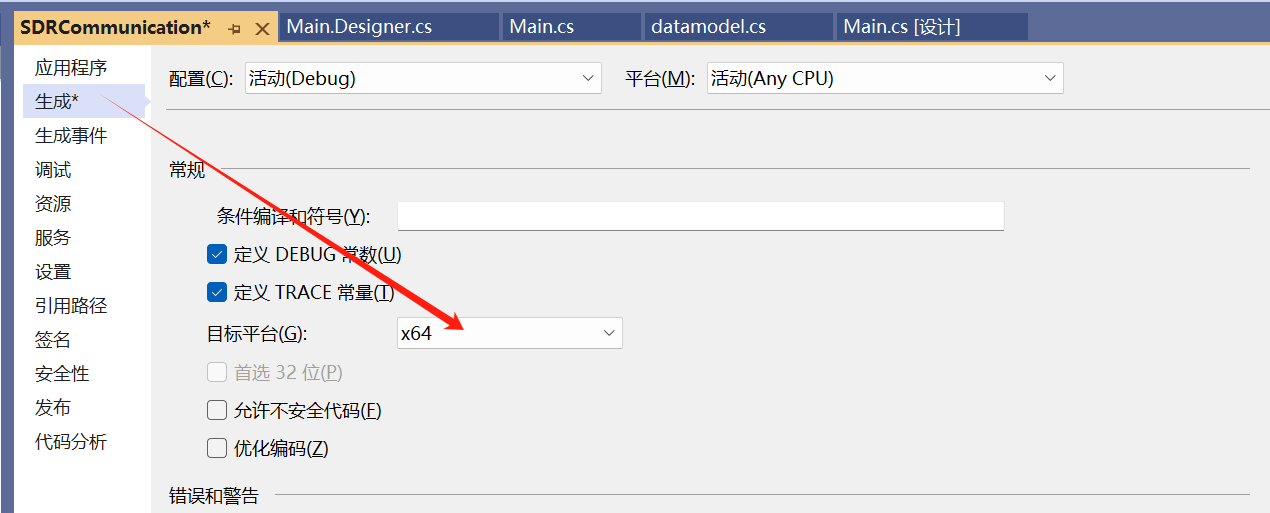
C#(winform) 调用MATLAB函数
测试环境 VisualStudio2022 / .NET Framework 4.7.2 Matlab2021b 参考:C# Matlab 相互调用 Matlab 1、编写Matlab函数 可以没有任何参数单纯定义matlab处理的函数,输出的数据都存在TXT中用以后期读取数据 function [result,m,n] TEST(list) % 计算…...
)
Kubernetes探索-Pod面试(补充)
针对上篇文章"kubernetes探索-Pod面试"做一点点补充... 1. 简述Pod的删除流程 1) kube-apiserver接收到用户的删除指令,默认等待30s(优雅退出时间),随后认为pod已死亡,将其标记为Terminating状态; 2) kubelet监控到pod…...

深入了解JUnit 5:新一代Java单元测试框架
深入了解JUnit 5:新一代Java单元测试框架 近年来,Java领域的单元测试框架发展迅速,而JUnit 5作为JUnit系列的最新版本,为开发人员提供了更多的功能和灵活性。在本文中,我们将介绍JUnit 5,并探讨其与JUnit 4…...
2024年清明节安装matlab 2024a
下载安装离线支持包SupportSoftwareDownloader_R2024a_win64,地址https://ww2.mathworks.cn/support/install/support-software-downloader.html,运行软件(自解压运行),登录账号(需要提前在官网注册&#x…...

关于PostgreSQL JDBC中的log输出是怎么回事?
微信公众号:数据库杂记 个人微信: _iihero 我是iihero. 也可以叫我Sean. iihero@CSDN(https://blog.csdn.net/iihero) Sean@墨天轮 (https://www.modb.pro/u/16258) 数据库领域的资深爱好者一枚。SAP数据库技术专家与架构师,PostgreSQL ACE. 水木早期数据库论坛发起人db2@…...
【科研笔记】知识星球不可选择内容爬虫
知识星球不可选择内容爬虫 1 背景2 实现3 拓展遗留问题1 背景 针对与知识星球中,电脑打开网页不可选择复制粘贴的问题,进行爬虫处理,获取网页的内容,并保存在本地 2 实现 需要下载python,和爬虫的第三方库selenium,可以查看博客中有关selenium的内容进行回顾。当前使用…...
)
[技术闲聊]我对电路设计的理解(二)
第一篇文章 [技术闲聊]我对电路设计的理解(一),看着是述说着应届生如何对待一份工作,其实也是我在过往以及以目前视野看过往的事情,自己的一种态度。谦虚,是一个不可多得的词汇,因为刚起步,学习的东西很多&…...
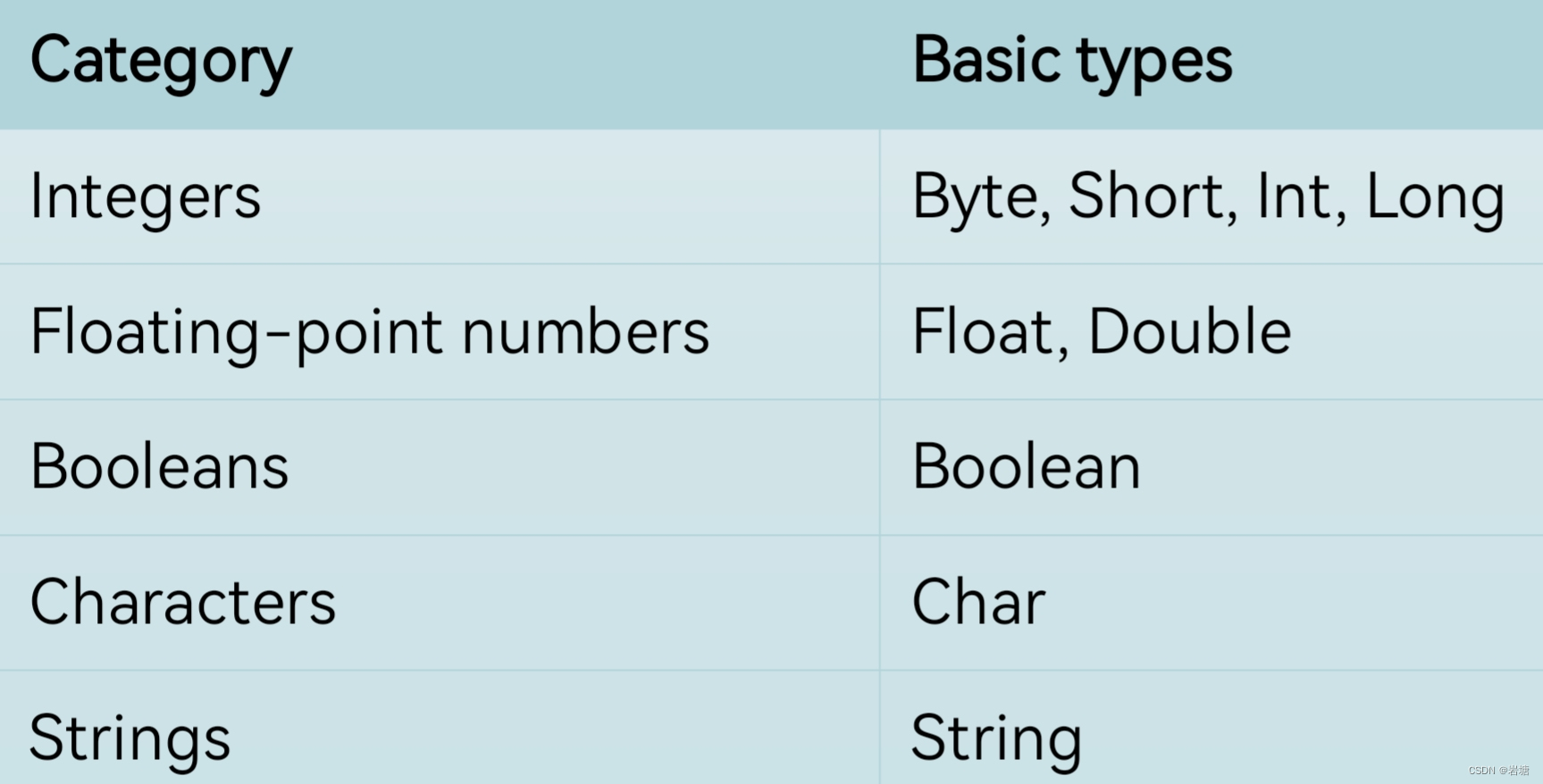
【Android、 kotlin】kotlin学习笔记
基本语法 fun main(){val a2var b "Hello"println("$ (a - 1} $b Kotlin!")} Variables 只赋值一次用val read-only variables with val 赋值多次用var mutable variables with var Standard output printin() and print() functions String templ…...

Debian 配置国内软件源
为什么需要? Debian安装好之后默认是没有软件源的,只能通过本身的光盘上的软件进行安装,这样明显是不能够满足我们的需要的,考虑到国内的上网速度以及环境,配置一个国内的阿里镜像源是最好的选择。 使用 sudo vim /…...
)
选数(dfs,isprime)
题目:P1036 [NOIP2002 普及组] 选数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) #include<bits/stdc.h> using namespace std; int n,k; int a[22]; long long ans; bool isprime(int n){for(int i2;i<sqrt(n);i){if(n%i0) return false;…...
RocketMQ(版本4.9.4)+RocketMQ_Dashbord环境搭建(生产者、消费者的前置环境搭建)
一、官方网站下载 RocketMQ源码包 https://rocketmq.apache.org/zh/docs/4.x/introduction/02quickstart 二、把rocketMQ上传到Linux环境下解压,编译,执行以下命令(需要提前装jdk和maven并配置好环境变量) unzip rocketmq-all-4…...

css隐藏溢出隐藏的滚动条
msOverflowStyle: none: 这个属性用于在 Internet Explorer 浏览器中定义滚动条的样式。将其设置为 none 可以隐藏滚动条。 scrollbarWidth: none: 这个属性用于定义滚动条的宽度。将其设置为 none 可以隐藏滚动条。这个属性在一些新的浏览器中被支持,如 Firefox。…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
