电工技术学习笔记——直流电路及其分析方法
一、直流电路

电路的组成
1. 电压和电流的参考方向
-
电压(Voltage):电压是电场力对电荷产生的作用,表示为电荷单位正电荷所具有的能量。在电路中,电压通常被定义为两点之间的电势差,具有方向性,沿着电场方向从高电势指向低电势,即电压降的方向。这个方向也被称为电压的极性。

-
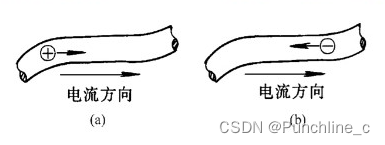
电流(Current):电流是单位时间内电荷通过某一截面的量,通常用符号"i"表示。电流有方向,正电流表示电荷流动方向与某个参考方向相同,负电流表示电荷流动方向与参考方向相反
2. 电源的工作状态
- 电源:电源是提供电能供给电路或设备的装置。它可以是直流电源或交流电源。电源的工作状态通常分为工作状态和断开状态两种。在工作状态下,电源提供电流或电压给电路或设备;而在断开状态下,电源不提供电流或电压输出。
3. 欧姆定律
- 欧姆定律(Ohm’s Law):欧姆定律是电学基本定律之一,它表明电压、电流和电阻之间的关系。它的数学表达式为 V = I * R,其中 V 是电压(单位:伏特),I 是电流(单位:安培),R 是电阻(单位:欧姆)。该定律说明了在恒定温度下,电压与电流成正比,电压与电阻成正比,而电流与电阻成反比。

4. 基尔霍夫定律
- 基尔霍夫定律:基尔霍夫定律是描述电路中电压和电流分布的重要定律。
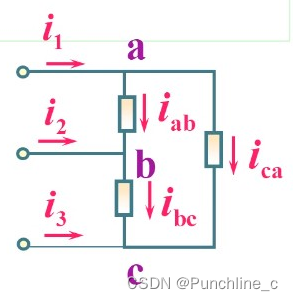
- 基尔霍夫第一定律(KCL)(节点定律):一个闭合电路中,任意一个节点处的入流电流等于出流电流的代数和。

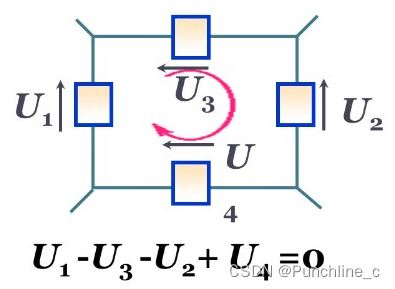
- 基尔霍夫第二定律(KVL)(环路定律):在任一瞬间,沿任一回路绕行方向,回路中各段电压的代数和恒等于0。
- 基尔霍夫第一定律(KCL)(节点定律):一个闭合电路中,任意一个节点处的入流电流等于出流电流的代数和。
5. 电位的概念及计算
-
电位:电位是指电荷在电场中由于所处位置的不同而具有的能量差异。在电路中,电位通常指电压,即某一点相对于某一参考点的电势差。电位的单位是伏特(V)。
-
电位的计算:电位差等于两点之间的电压。如果知道电压源的电压和电阻的电流,则可以使用欧姆定律计算两点之间的电压。另外,基尔霍夫定律也提供了一种计算电压的方法,特别是在复杂的电路中。
二、直流电路的分析方法
1. 等效变换
- 等效变换:在分析电路时,可以将复杂的电路元件或网络简化为等效的电路,以便更容易地进行分析和计算。例如,电阻网络可以用其等效电阻替换,电压源和电流源可以用其等效电压或电流替换。
- 示例:将若干电阻串联或并联后,用一个等效的电阻替代它们。例如,将两个串联的 10 欧姆电阻替换为一个 20 欧姆的等效电阻。
2. 支路电流法
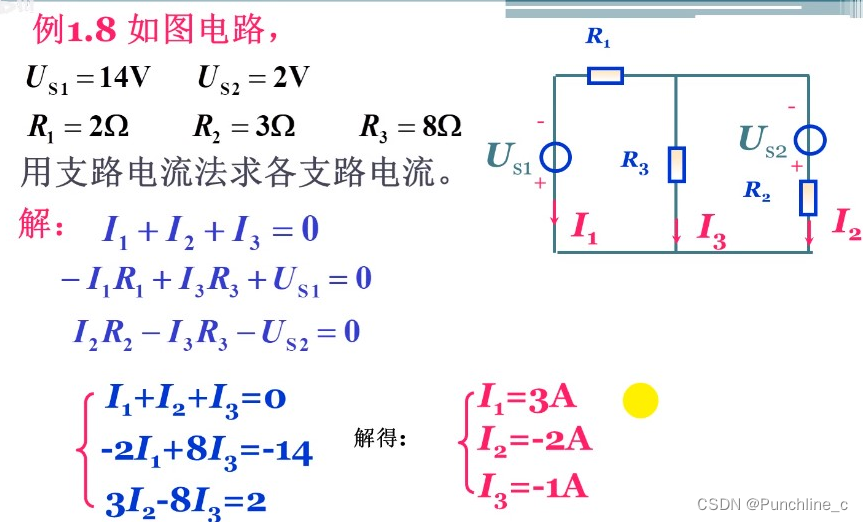
- 支路电流法:支路电流法是一种基于电流的分析方法,它将电路中的各支路看作独立的电流来源,并根据基尔霍夫定律和欧姆定律建立支路电流方程组,从而求解电路中各支路的电流。
- 示例:考虑一个简单的电路,其中有两个并联的电阻和一个串联的电压源。使用支路电流法,可以将电路中的电流流向每个支路,并根据欧姆定律和基尔霍夫定律列出方程组,进而求解电路中的电流。
3. 叠加定理
- 叠加定理:叠加定理适用于线性电路,它指出复杂电路中的任意一个响应可以分解为各个独立电源作用下的单个响应之和。因此,可以分别考虑每个电源对电路的影响,然后将它们叠加起来得到最终结果。
- 示例:考虑一个电路中有两个电压源,分别为 5 伏特和 10 伏特,与一个串联的电阻。使用叠加定理,可以分别计算每个电压源作用下的电流,然后将它们相加以得到电路中的总电流。
 注:功率不可叠加(P=I^2*R)
注:功率不可叠加(P=I^2*R)
4. 戴维宁定理
- 戴维宁定理:戴维宁定理是一种基于等效变换的分析方法,它将电路中的电压源和电流源分别替换为其内部电阻的等效电路,从而简化电路结构,便于分析。
- 示例:考虑一个电路中有一个电压源和一个电流源,与一些电阻串联并并联。使用戴维宁定理,可以将电压源和电流源替换为其内部电阻的等效电路,从而简化整个电路,便于分析。
5. 结点电压法
- 结点电压法:结点电压法是一种基于电压的分析方法,它将电路中的每个节点的电压作为未知数,根据基尔霍夫定律和欧姆定律建立节点电压方程组,从而求解电路中各节点的电压。
相关文章:

电工技术学习笔记——直流电路及其分析方法
一、直流电路 电路的组成 1. 电压和电流的参考方向 电压(Voltage):电压是电场力对电荷产生的作用,表示为电荷单位正电荷所具有的能量。在电路中,电压通常被定义为两点之间的电势差,具有方向性,…...

详解python中的迭代
如果给定一个list或tuple,我们可以通过for循环来遍历这个list或tuple,这种遍历我们称为迭代(Iteration)。 在Python中,迭代是通过for ... in来完成的,而很多语言比如C语言,迭代list是通过下标完…...
)
机器学习模型——集成算法(三)
前面我们说了bagging算法和Boosting算法 接下来我们学习Adaboost算法 Adaboost基本概念: AdaBoost (Adaptive Boosting,自适应提升): 算法原理是将多个弱学习器进行合理的结合,使其成为一个强学习器。 Adaboost采用…...
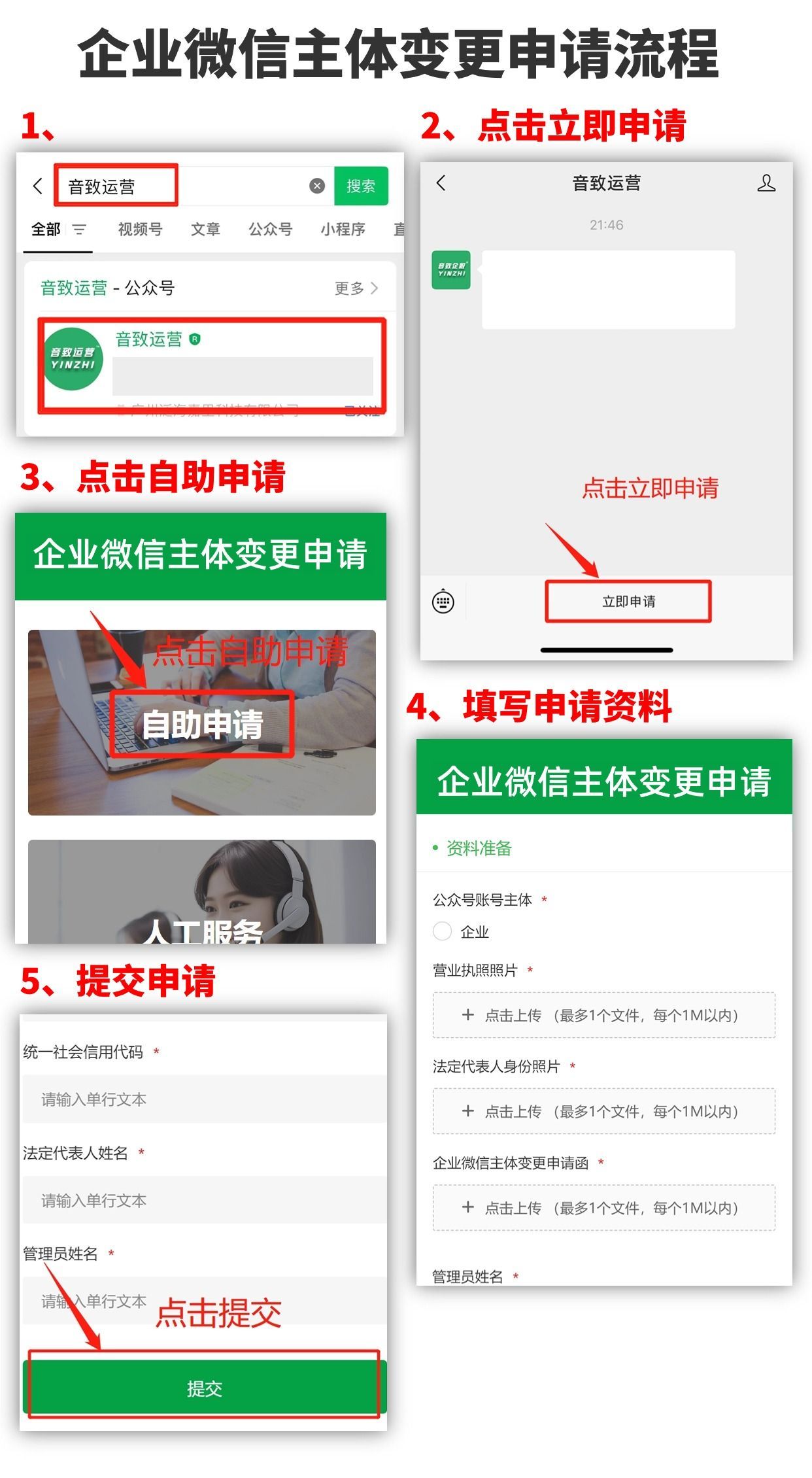
企业微信企业主体变更认证介绍
企业微信变更主体有什么作用? 说一个自己亲身经历的事情,当时我在一家教育公司做运营,公司所有客户都是通过企业微信对接的。后来行业整顿,公司不得不注销,换了营业执照打算做技能培训,但发现注销后原来的企…...

如何降低AI功耗? —— 超低功耗的仿生硬件
一、背景 仿生硬件(Bionic Hardware)这一术语通常指的是受自然界的生物系统启发而设计制造的电子或机械硬件设备,它们在功能、结构、材料、能源效率等方面模仿生物体的特性,以实现更高效、智能、自适应或环境友好的性能。在人工智…...

原型模式详解
原型模式简单的理解来说,就是复制品,用一个已经做好的成品作为原型,然后通过复制它得到新的产品。就好像细胞分裂一样。用Java来说,就是用对象创建对象,而不是通过类来创建对象。 原型模式的目的是从原型实例克隆出新的实例 ,对于那些有非常复杂的初始化过程的对象或者是…...

嵌入式开发中状态模式实现
文章目录 状态模式代码实现代码解释小结 状态模式 状态模式(State Pattern)是一种行为设计模式,它允许对象在内部状态改变时改变它的行为。在嵌入式系统中,状态模式尤其适用于那些根据外部事件或内部条件频繁改变状态并且每种状态…...

目标检测——车牌数据集
一、重要性及意义 交通安全与管理:车牌检测和识别技术有助于交通管理部门快速、准确地获取车辆信息,从而更有效地进行交通监控和执法。例如,在违规停车、超速行驶等交通违法行为中,该技术可以帮助交警迅速锁定违规车辆࿰…...

FOC算法中为啥用PWM触发ADC中断
在FOC(Field Oriented Control,场向量控制)算法中,为什么要使用PWM(Pulse Width Modulation,脉宽调制)触发ADC(Analog-to-Digital Converter,模数转换器)中断…...

2024.4.5学习记录————嵌入式学习内容
2024.4.5学习记录————嵌入式学习内容 C语言 指针,位操作,结构体字节对齐,位段,宏的高级运用 C 基础特性:类,对象,派生,继承,运算符重载,友元…...
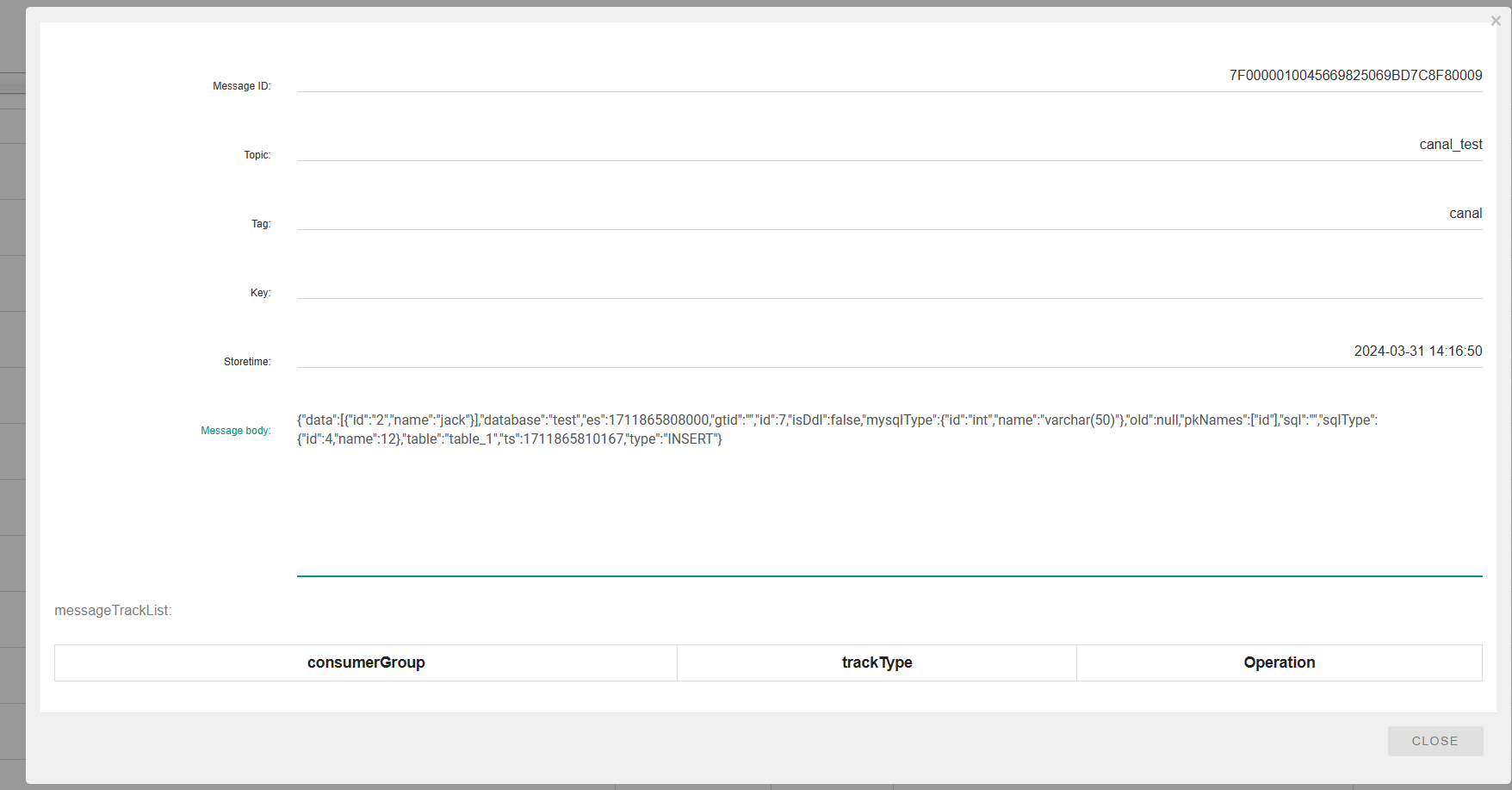
k8s 部署 canal 集群,RocketMQ 模式
k8s 部署 canal 集群,RocketMQ 模式 k8s 部署 canal 集群,RocketMQ 模式前提MySQLRocketMQ制作 canal-admin、canal-server 镜像 部署 zookeeper部署 canal-admin部署 canal-server测试 k8s 部署 canal 集群,RocketMQ 模式 前提 MySQL 开启…...

Android+OnnxRuntime+Opencv+Onnx模型操作图片擦除多余内容
今年来AI的发展非常迅速,在工业、医疗等等行业逐渐出现相应的解决方案,AI也逐渐成为各行业基础设施建设重要的一环,未来发展的大趋势,不过这也需要一个漫长的过程,需要很多技术型人才加入其中,除了工业设施的基础建设,在娱乐方向也有很多有趣的能力,不如图片/视频换背景…...

【CANoe】CAPL_E2E测试-验证报文中的CRC值是否正确
文章目录 一、背景二、CRC校验算法实现_dll制作三、CAPL脚本编写四、测试结果4.1、Write输出窗口4.2、测试报告截图一、背景 在嵌入式软件开发过程中,对于一些报文,需要实现安全发送与安全接收,这就涉及到CRC和RollingCounter。整车和MCU通讯的报文需要对方进行校验才能正确…...

Linux云计算之网络基础8——IPV6和常用网络服务
目录 一、IPV6基础 IPV6详解 IPv6数据报的基本首部 IPv6数据报的扩展首部 IPv6地址的表示方法 IPv6地址分类 网际控制报文协议ICMPv6 二、cisco基于IPV6的配置 cisco基于IPV6的配置步骤 模拟配置 三、HTML基础介绍 文档的结构 动手操作一下 四、常用网络服务介绍…...

页面刚加载的时候显示自己定义的{{***}}然后一闪而过
这时候别用插值表达式语法了,直接用v-text或者v-html就能解决这个问题 但是有个问题,如下图所示: 具体bind使用方式,如下图所示: 但是v-bind也可以进行简写,就是去掉v-bind,直接写:…...
python批量转化pdf图片为jpg图片
1.把pdf图片批量转为jpg;需要注意的是,需要先安装poppler这个软件,具体安装教程放在下面代码中了 2.代码 #poppler安装教程参考:https://blog.csdn.net/wy01415/article/details/110257130 #windows上poppler下载链接:…...
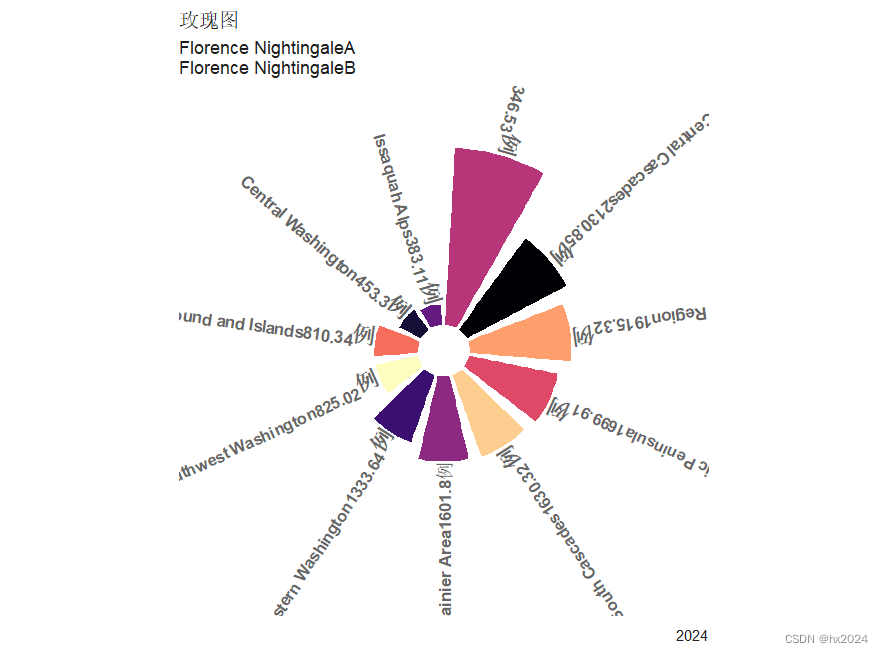
玫瑰图和雷达图(自备)
目录 玫瑰图 数据格式 绘图基础 绘图升级(文本调整) 玫瑰图 下载数据data/2020/2020-11-24 mirrors_rfordatascience/tidytuesday - 码云 - 开源中国 (gitee.com) R语言绘图—南丁格尔玫瑰图 - 知乎 (zhihu.com) 数据格式 rm(list ls()) libr…...
动态规划基础
动态规划 1、动态规划的概念 简称DP,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。常常适用于有重叠子问题和最优子结构性质的问题。 简单来说,就是给定一个问题,把它拆成一个个子问题,查到子问题可以直接解决。然后把子问题答案保存起来,以减少重复计算…...

kubeadm部署的k8s1.29集群证书更新
1、查看证书有效期 kubeadm certs check-expiration更新证书前: [check-expiration] Reading configuration from the cluster... [check-expiration] FYI: You can look at this config file with kubectl -n kube-system get cm kubeadm-config -o yamlCERTIFIC…...

【A 类比赛】大学生学科竞赛智慧应用场景题目大全
智能应用的多彩场景:未来生活的无限可能 随着科技的飞速发展,智能应用已经渗透到我们生活的方方面面,它们不仅极大地提高了工作效率,也丰富了我们的生活体验。从家庭到工作场所,从城市到乡村,智能应用正在…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
