tigramite教程(七)使用TIGRAMITE 进行条件独立性测试
文章目录
- 概述
- 1 连续数值变量
- 1.1 ParCorr 偏相关(ParCorr类)
- 1.2 鲁棒偏相关(RobustParCorr)
- 非线性检验
- 1.3 GPDC
- 1.4 CMIknn
- 2a. 分类/符号时间序列
- 2b. 混合分类/连续时间序列
- 多变量X和Y的测试
概述
这个表格概述了 X ⊥ Y ∣ Z X\perp Y | Z X⊥Y∣Z的测试及其相关的假设
| 条件独立性检验 | 假设条件 |
|---|---|
| ParCorr | 连续变量 X , Y , Z X,Y,Z X,Y,Z,具有线性依赖关系和高斯噪声; X , Y X,Y X,Y必须是单变量 |
| RobustParCorr | 连续变量 X , Y , Z X,Y,Z X,Y,Z,具有线性依赖关系,对不同边缘分布具有鲁棒性; X , Y X,Y X,Y必须是单变量 |
| ParCorrWLS | 连续变量 X , Y , Z X,Y,Z X,Y,Z,具有线性依赖关系,可以处理异方差依赖关系; X , Y X,Y X,Y必须是单变量 |
| GPDC / GPDCtorch | 连续变量 X , Y , Z X,Y,Z X,Y,Z,具有加性依赖关系; X , Y X,Y X,Y必须是单变量 |
| CMIknn | 连续变量 X , Y , Z X,Y,Z X,Y,Z,具有更一般的依赖关系(基于排列的检验); X , Y X,Y X,Y可以是多变量 |
| Gsquared | 离散/分类变量 X , Y , Z X,Y,Z X,Y,Z; X , Y X,Y X,Y必须是单变量 |
| CMIsymb | 离散/分类变量 X , Y , Z X,Y,Z X,Y,Z(基于排列的检验); X , Y X,Y X,Y 可以是多变量 |
| RegressionCI | 混合数据集,包含单变量离散/分类和(线性)连续变量 X , Y , Z X,Y,Z X,Y,Z; X , Y X,Y X,Y必须是单变量 |
| PairwiseMultCI | 元条件独立性检验,将上述每个单变量检验转变为多变量检验,包括可能有助于增加效应大小的方法 |
在概述教程中讨论的密度图可以帮助选择使用哪种测试。
需要注意的是,那些假设条件较少的测试通常比假设条件较多的测试具有更低的检测能力。例如,对于实际上是线性的依赖关系,ParCorr的效果会比CMIknn好得多。此外,非参数测试在计算上要昂贵得多。
# Imports
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
## use `%matplotlib notebook` for interactive figures
# plt.style.use('ggplot')
import sklearnimport tigramite
from tigramite import data_processing as pp
from tigramite.toymodels import structural_causal_processes as toysfrom tigramite import plotting as tp
from tigramite.pcmci import PCMCIfrom tigramite.independence_tests.parcorr import ParCorr
from tigramite.independence_tests.robust_parcorr import RobustParCorr
from tigramite.independence_tests.parcorr_wls import ParCorrWLS
from tigramite.independence_tests.gpdc import GPDC
from tigramite.independence_tests.cmiknn import CMIknn
from tigramite.independence_tests.cmisymb import CMIsymb
from tigramite.independence_tests.gsquared import Gsquared
from tigramite.independence_tests.regressionCI import RegressionCI
1 连续数值变量
1.1 ParCorr 偏相关(ParCorr类)
在概述教程中有解释。
1.2 鲁棒偏相关(RobustParCorr)
如果在数据中仍然存在线性依赖关系,但分布又不是高斯分布,建议使用鲁棒偏相关(RobustParCorr)测试。这种测试在进行偏相关测试之前,会先将数据转换为正态分布1。
在这里,我们还展示了新的函数toys.generate_structural_causal_process,它允许随机创建具有一定数量参数的结构因果过程模型(详见文档说明)。在接下来的示例中,噪声项来自于极值Weibull分布和均匀分布。此外,我们还应用了一些多项式变换,使数据变得更加极端。
# np.random.seed(1)
T = 500
links, noises = toys.generate_structural_causal_process(N=3, L=4, dependency_funcs=['linear'], dependency_coeffs=[-0.5, 0.5], auto_coeffs=[0.3, 0.5], contemp_fraction=0.,max_lag=2, noise_dists=['weibull', 'uniform'],noise_means=[0.],noise_sigmas=[1., 1.5],noise_seed=5,seed=9)
for j in links:print(j, [(link[0], link[1], link[2].__name__) for link in links[j]])print(noises[j].__name__)
data, nonstat = toys.structural_causal_process(links,T=T, noises=noises)
data[:,0] = data[:,0] + 0.3*data[:,0]**3
data[:,1] = data[:,1] + 0.3*data[:,1]**5
data[:,2] = np.sign(data[:,2])*data[:,2]**2
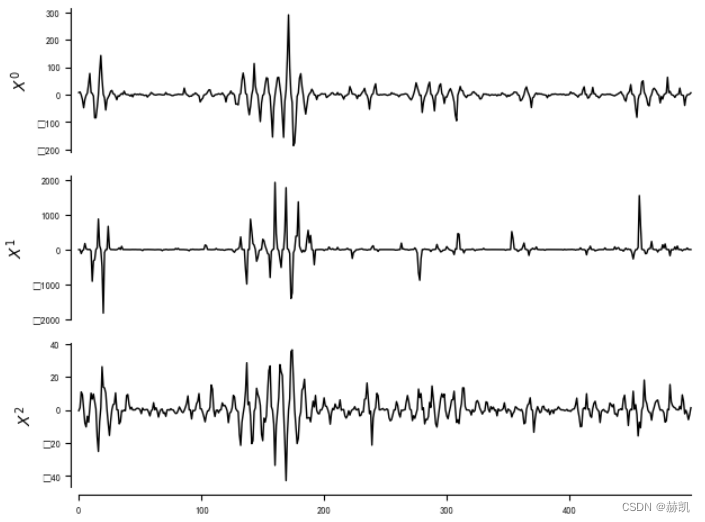
var_names = [r'$X^0$', r'$X^1$', r'$X^2$']dataframe = pp.DataFrame(data, var_names=var_names)
tp.plot_timeseries(dataframe)
0 [((0, -1), 0.5, ‘linear’), ((2, -1), -0.5, ‘linear’), ((1, -2), 0.5, ‘linear’)]
weibull
1 [((1, -1), 0.3, ‘linear’), ((0, -2), -0.5, ‘linear’)]
weibull
2 [((2, -1), 0.3, ‘linear’), ((0, -2), 0.5, ‘linear’)]
uniform
# Init
pcmci_robust_parcorr = PCMCI(dataframe=dataframe, cond_ind_test=RobustParCorr())
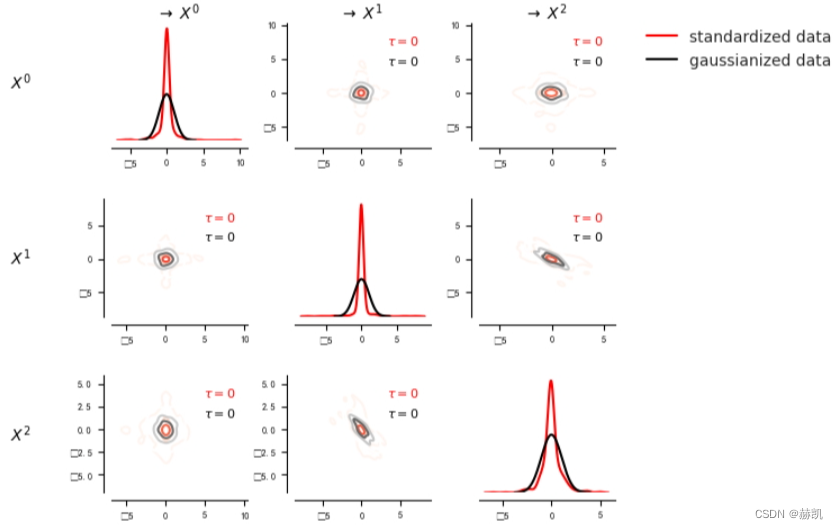
我们可以使用密度图功能来展示偏斜的边缘和联合密度。在这里,我们将偏斜的数据标准化,以显示它明显非高斯分布。
# tp.plot_densityplots(dataframe=dataframe, add_densityplot_args={'matrix_lags':matrix_lags}); plt.show()
# correlations = pcmci_robust_parcorr.get_lagged_dependencies(tau_max=20, val_only=True)['val_matrix']
# matrix_lags = np.argmax(np.abs(correlations), axis=2)
matrix_lags = Nonematrix = tp.setup_density_matrix(N=dataframe.N, var_names=dataframe.var_names)# Standardize to better compare skewness with gaussianized data
dataframe.values[0] -= dataframe.values[0].mean(axis=0)
dataframe.values[0] /= dataframe.values[0].std(axis=0)matrix.add_densityplot(dataframe=dataframe, matrix_lags=matrix_lags, label_color='red', label="standardized data",snskdeplot_args = {'cmap':'Reds', 'alpha':1., 'levels':4})# Transform data to normal marginals
data_normal = pp.trafo2normal(data)
dataframe_normal = pp.DataFrame(data_normal, var_names=var_names)matrix.add_densityplot(dataframe=dataframe_normal, matrix_lags=matrix_lags, label_color='black', label="gaussianized data",snskdeplot_args = {'cmap':'Greys', 'alpha':1., 'levels':4})
matrix.adjustfig()
# plt.show()
pcmci_parcorr = PCMCI(dataframe=dataframe, cond_ind_test=ParCorr())
results = pcmci_parcorr.run_pcmci(tau_max=2)pcmci_robust_parcorr = PCMCI(dataframe=dataframe, cond_ind_test=RobustParCorr())
results_robust = pcmci_robust_parcorr.run_pcmci(tau_max=2)fig, axes = plt.subplots(nrows=1, ncols=3)
axes[0].set_title("True graph")
tp.plot_graph(graph=pcmci_robust_parcorr.get_graph_from_dict(links, tau_max=None),var_names=var_names,fig_ax=(fig, axes[0]),show_colorbar=False,)axes[1].set_title("ParCorr")
tp.plot_graph(val_matrix=results['val_matrix'],graph=results['graph'],var_names=var_names,fig_ax=(fig, axes[1]),show_colorbar=False,)axes[2].set_title("RobustParCorr")
tp.plot_graph(val_matrix=results_robust['val_matrix'],graph=results_robust['graph'],var_names=var_names,fig_ax=(fig, axes[2]),show_colorbar=False,)
plt.show()
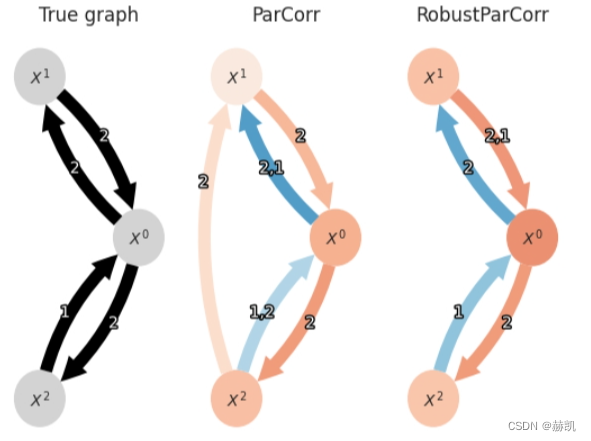
鲁棒偏相关(右图)在这里比标准的偏相关(左图)产生更可靠的结果,因为边缘分布事先被转换为正态分布。
在教程tigarite_tutorial_heteroskedastic_ParCorrWLS中,我们介绍了另一种适用于异方差数据的偏相关版本,称为ParCorrWLS。
非线性检验
如果存在非线性依赖关系,建议使用非参数检验。
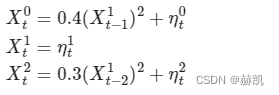
random_state = np.random.default_rng(seed=42)
data = random_state.standard_normal((500, 3))
for t in range(1, 500):data[t, 0] += 0.4*data[t-1, 1]**2data[t, 2] += 0.3*data[t-2, 1]**2
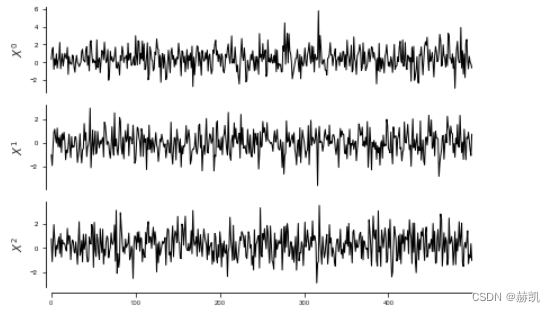
var_names = [r'$X^0$', r'$X^1$', r'$X^2$']dataframe = pp.DataFrame(data, var_names=var_names)
tp.plot_timeseries(dataframe); plt.show()
pcmci_parcorr = PCMCI(dataframe=dataframe, cond_ind_test=ParCorr(),verbosity=0)
results = pcmci_parcorr.run_pcmci(tau_max=2, pc_alpha=0.2, alpha_level = 0.01)
tp.plot_graph(val_matrix=results['val_matrix'],graph=results['graph'],var_names=var_names,show_colorbar=False,)
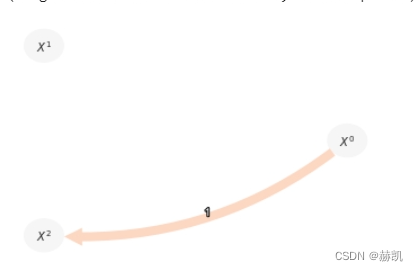
偏相关在这里有两个失败之处:(1)它无法检测到两个非线性链接;(2)它错误地检测到了一个链接,因为它同样无法排除非线性依赖。
1.3 GPDC
Tigramite通过基于高斯过程回归和残差上的距离相关性(GPDC)的测试来覆盖非线性加性依赖关系。对于GPDC,没有可用的距离相关性(DC)的解析空模型分布。为了进行显著性检验,Tigramite通过参数significance = 'analytic'预先计算每个样本大小的分布(存储在内存中),从而避免了对每个条件独立性测试进行计算成本高昂的排列测试(significance = 'shuffle_test')。高斯过程回归使用sklearn的默认参数执行,除了核函数在这里默认为径向基函数+一个白噪声核(这两个超参数在内部被优化),以及假定的噪声水平alpha被设置为零,因为我们添加了一个白噪声核。这些和其他参数可以通过gp_params字典来设置。有关进一步讨论,请参见sklearn的文档。还存在一个模块(gpdc_torch.py),它利用gpytorch在GPU上进行更快的计算。
gpdc = GPDC(significance='analytic', gp_params=None)
pcmci_gpdc = PCMCI(dataframe=dataframe, cond_ind_test=gpdc,verbosity=0)
与偏相关(ParCorr)相比,非线性链接被GPDC正确检测到。
results = pcmci_gpdc.run_pcmci(tau_max=2, pc_alpha=0.1, alpha_level = 0.01)
tp.plot_graph(val_matrix=results['val_matrix'],graph=results['graph'],var_names=var_names,show_colorbar=False,)
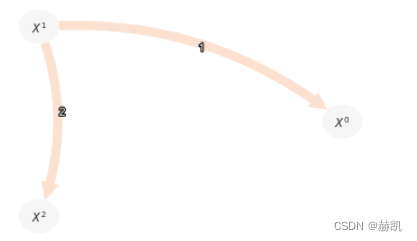
作为一个简短的离题,我们可以通过观察散点图来了解GPDC是如何工作的。
array, dymmy, dummy, dummy = gpdc._get_array(X=[(0, -1)], Y=[(2, 0)], Z=[(1, -2)], tau_max=2)
x, meanx = gpdc._get_single_residuals(array, target_var=0, return_means=True)
y, meany = gpdc._get_single_residuals(array, target_var=1, return_means=True)fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(8,3))
axes[0].scatter(array[2], array[0], color='grey', alpha=0.3)
axes[0].scatter(array[2], meanx, color='black')
axes[0].set_title("GP of %s on %s" % (var_names[0], var_names[1]) )
axes[0].set_xlabel(var_names[1]); axes[0].set_ylabel(var_names[0])
axes[1].scatter(array[2], array[1], color='grey', alpha=0.3)
axes[1].scatter(array[2], meany, color='black')
axes[1].set_title("GP of %s on %s" % (var_names[2], var_names[1]) )
axes[1].set_xlabel(var_names[1]); axes[1].set_ylabel(var_names[2])
axes[2].scatter(x, y, color='red', alpha=0.3)
axes[2].set_title("DC of residuals:" "\n val=%.3f / p-val=%.3f" % (gpdc.run_test(X=[(0, -1)], Y=[(2, 0)], Z=[(1, -2)], tau_max=2)) )
axes[2].set_xlabel("resid. "+var_names[0]); axes[2].set_ylabel("resid. "+var_names[2])
plt.tight_layout()
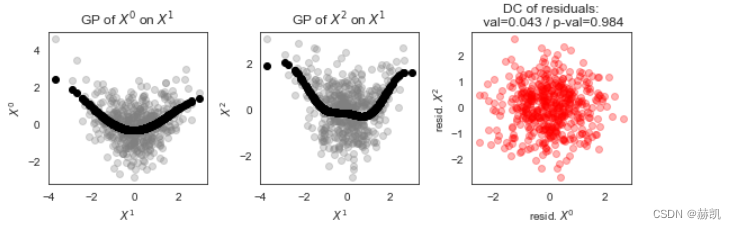
让我们来看一个具有乘性噪声的模型中更为非线性的依赖关系:
random_state = np.random.default_rng(seed=11)
data = random_state.standard_normal((600, 3))
for t in range(1, 600):data[t, 0] *= 0.2*data[t-1, 1]data[t, 2] *= 0.3*data[t-2, 1]
dataframe = pp.DataFrame(data, var_names=var_names)
tp.plot_timeseries(dataframe); plt.show()

由于乘性噪声违反了GPDC所基于的加性依赖的假设,虚假的链接被错误地检测出来,因为它无法被排除条件。然而,与ParCorr相比,两个真实的链接被检测出来,因为距离相关性(DC)可以检测到任何类型的依赖关系(底层的sklearn高斯过程函数可能会发出警告):
pcmci_gpdc = PCMCI(dataframe=dataframe, cond_ind_test=gpdc)
results = pcmci_gpdc.run_pcmci(tau_max=2, pc_alpha=0.1, alpha_level = 0.01)
tp.plot_graph(val_matrix=results['val_matrix'],graph=results['graph'],var_names=var_names,show_colorbar=False,)
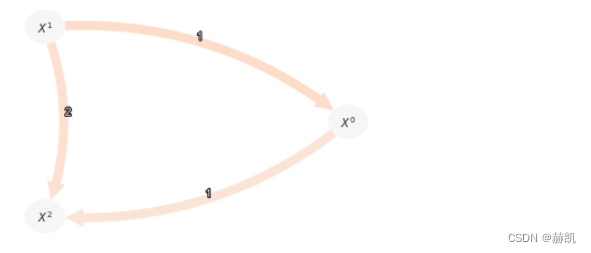
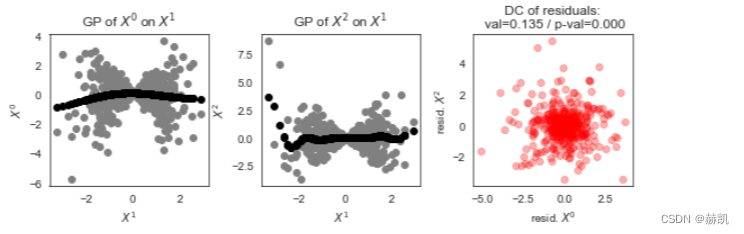
在这里的散点图中,我们可以看到高斯过程无法很好地拟合依赖关系,因此残差不是独立的。
array, dymmy, dummy, dummy = gpdc._get_array(X=[(0, -1)], Y=[(2, 0)], Z=[(1, -2)], tau_max=2)
x, meanx = gpdc._get_single_residuals(array, target_var=0, return_means=True)
y, meany = gpdc._get_single_residuals(array, target_var=1, return_means=True)fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(8,3))
axes[0].scatter(array[2], array[0], color='grey')
axes[0].scatter(array[2], meanx, color='black')
axes[0].set_title("GP of %s on %s" % (var_names[0], var_names[1]) )
axes[0].set_xlabel(var_names[1]); axes[0].set_ylabel(var_names[0])
axes[1].scatter(array[2], array[1], color='grey')
axes[1].scatter(array[2], meany, color='black')
axes[1].set_title("GP of %s on %s" % (var_names[2], var_names[1]) )
axes[1].set_xlabel(var_names[1]); axes[1].set_ylabel(var_names[2])
axes[2].scatter(x, y, color='red', alpha=0.3)
axes[2].set_title("DC of residuals:" "\n val=%.3f / p-val=%.3f" % (gpdc.run_test(X=[(0, -1)], Y=[(2, 0)], Z=[(1, -2)], tau_max=2)) )
axes[2].set_xlabel("resid. "+var_names[0]); axes[2].set_ylabel("resid. "+var_names[2])
plt.tight_layout()
1.4 CMIknn
Tigramite中实现的最通用的条件独立性测试是基于使用k-最近邻估计器估计的条件互信息(CMIknn)。这个测试在下面的论文中有描述:
Runge, Jakob. 2018. “基于条件互信息最近邻估计器的条件独立性测试。” 载于第21届国际人工智能与统计会议论文集。
CMIknn不涉及对依赖关系的明确假设。然而,由于密度是通过局部样本超点隐式近似的,因此有一个假设是这些超立方体内密度是恒定的。参数knn决定了超立方体的大小,即(数据自适应的)局部长度尺度。
现在我们甚至不能预计算空模型分布,因为CMIknn不像GPDC那样基于残差,空模型分布依赖于更多因素。因此,我们使用significance='shuffle_test'在每个单独的测试中生成它。测试的洗牌测试 I ( X ; Y ∣ Z ) = 0 I(X;Y|Z)=0 I(X;Y∣Z)=0随机 X X X值是局部的:每个样本点 x x x的值被随机映射到其最近邻居中的一个(shuffle_neighbors参数)在子空间 Z Z Z中。另一个可选参数是transform,它指定在CMI估计之前是否转换数据。新的默认值是transform=ranks,它比旧的transform=standardize效果更好。下面的单元可能需要几分钟时间。
# cmi_knn = CMIknn(significance='shuffle_test', knn=0.1, shuffle_neighbors=5, transform='ranks', sig_samples=200)
# pcmci_cmi_knn = PCMCI(
# dataframe=dataframe,
# cond_ind_test=cmi_knn,
# verbosity=0)
# results = pcmci_cmi_knn.run_pcmci(tau_max=2, pc_alpha=0.05, alpha_level = 0.01)
# tp.plot_graph(
# val_matrix=results['val_matrix'],
# graph=results['graph'],
# var_names=var_names,
# link_colorbar_label='cross-MCI',
# node_colorbar_label='auto-MCI',
# vmin_edges=0.,
# vmax_edges = 0.3,
# edge_ticks=0.05,
# cmap_edges='OrRd',
# vmin_nodes=0,
# vmax_nodes=.5,
# node_ticks=.1,
# cmap_nodes='OrRd',
# ); plt.show()
在这里,CMIknn正确地检测到了真实的链接,并且也揭示了虚假的链接。虽然CMIknn现在可能看起来是最好的独立性测试选择,我们必须注意到,这种通用性是以更低的检测能力为代价的,即当依赖关系实际上遵循某种参数形式时。那么,ParCorr或GPDC是更有力的措施。当然,ParCorr也比GPDC更好地检测线性链接。
另外需要注意的是:由于洗牌测试,CMIknn的计算成本非常高。你可以通过sig_samples参数减少洗牌样本的数量(以增加p值估计的误差为代价)。
或者,你可以使用significance='fixed_thres'选项。然后,pc_alpha被解释为任何条件独立性测试中的(单边)阈值 I ∗ I^* I∗。然后不会进行条件独立性假设检验。对于测试统计量 I ( X ; Y ∣ Z ) I(X;Y|Z) I(X;Y∣Z)
的条件独立性的标准则是
I ( X ; Y ∣ Z ) < I ∗ I(X;Y|Z)<I^* I(X;Y∣Z)<I∗
I ∗ I^* I∗应被视为超参数。请注意,为CMIknn选择 I ∗ I^* I∗是棘手的,因为 I ( X ; Y ∣ Z ) I(X;Y|Z) I(X;Y∣Z)的值取决于变量的维度,由于有限样本的估计偏差。好的一面是,即使这样,CMIknn也相当快。
然后,你也可以使用像pc_alpha = [0.001, 0.005, 0.01, 0.05](或任何其他你选择的阈值列表)。然后计算所有这些阈值的图形,并使用CMIknn的(新)get_model_selection_criterion函数在这些图形中选择。该函数使用sklearn的cross_val_score(基于模型选择_folds的k折交叉验证集)和KNeighborsRegressor模型(与估计器的邻居数量相同,但使用标准的欧几里得范数)在每个节点上使用其在给定阈值产生的图形中的父节点。它将返回最小分数(预测误差)的结果。
这个选项只对依赖于排列测试的条件独立性测试有意义,这些测试是CMIknn和CMIsymb.
# Pick pc_alpha here interpreted as fixed threshold with significance='fixed_thres'
pc_alpha = 0.05 #[0.001, 0.005, 0.01, 0.025, 0.05, 0.1]cmi_knn = CMIknn(significance='fixed_thres', model_selection_folds=3)
pcmci_cmi_knn = PCMCI(dataframe=dataframe, cond_ind_test=cmi_knn, verbosity=0)
results = pcmci_cmi_knn.run_pcmciplus(tau_max=2, pc_alpha=pc_alpha)
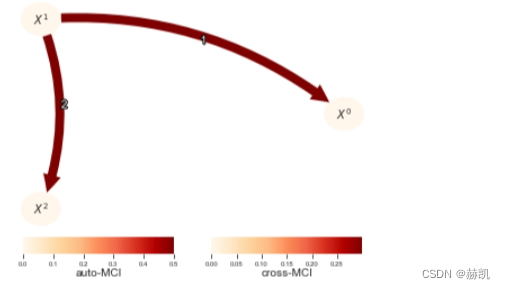
# if fixed_thres is used, pc_alpha (and alpha_level) is interpreted as a threshold on the test statistic.tp.plot_graph(val_matrix=results['val_matrix'],graph=results['graph'],var_names=var_names,link_colorbar_label='cross-MCI',node_colorbar_label='auto-MCI',vmin_edges=0.,vmax_edges = 0.3,edge_ticks=0.05,cmap_edges='OrRd',vmin_nodes=0,vmax_nodes=.5,node_ticks=.1,cmap_nodes='OrRd',); plt.show()
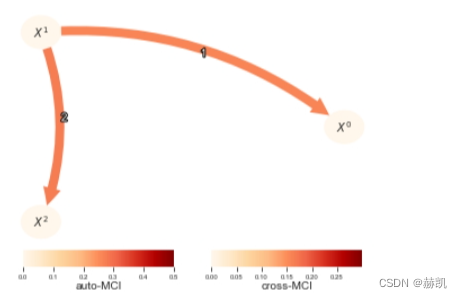
在这个例子中,选择 pc_alpha = [0.001, 0.005, 0.01, 0.025, 0.05, 0.1] 并不能得到正确的结果。阈值设定没有统计检验的严谨性,但可以帮助进行因果特征选择或在更大的机器学习流水线中使用因果发现等任务。
2a. 分类/符号时间序列
分类或符号(或离散)数据在值之间没有顺序或度量,比如苹果和梨子。为了适应这类时间序列,Tigramite包括了Gsquared和CMIsymb条件独立性测试。这两种测试都是直接从离散值的直方图估计得出的。为了获得空模型分布,Gsquared使用 x 2 x^2 x2分布(对于零条目调整自由度),这只在渐近情况下有效(取决于数据)。对于较小的样本量,使用CMIsymb类,它包括基于条件互信息的局部排列测试,CMIsymb的计算时间要比Gsquared长得多。
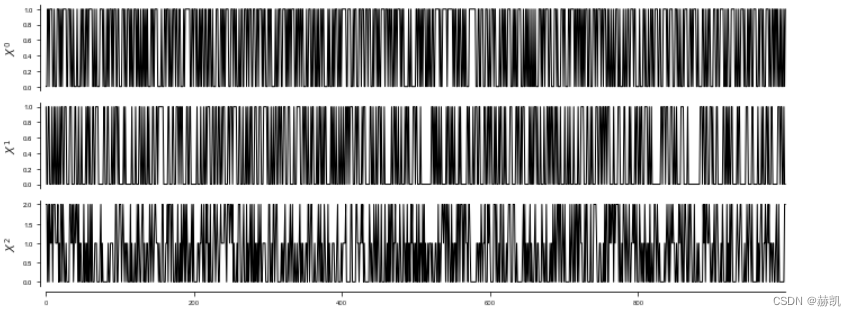
在下面的过程中, X 0 X^0 X0, X 1 X^1 X1有两个类别,而 X 2 X^2 X2有三个。 X 0 X^0 X0, X 2 X^2 X2的概率取决于 X 1 X^1 X1的概率,其中 X 1 X^1 X1充当混杂因子。
T = 1000
def get_data(T, seed=1):random_state = np.random.default_rng(seed)data = random_state.binomial(n=1, p=0.4, size=(T, 3))for t in range(T):prob = 0.4+data[t-1, 1].squeeze()*0.2data[t, 0] = random_state.choice([0, 1], p=[prob, 1.-prob])prob = 0.4+data[t-2, 1].squeeze()*0.2data[t, 2] = random_state.choice([0, 1, 2], p=[prob, (1.-prob)/2., (1.-prob)/2.])return data
dataframe = pp.DataFrame(get_data(T), var_names=var_names)
tp.plot_timeseries(dataframe, figsize=(10,4)); plt.show()
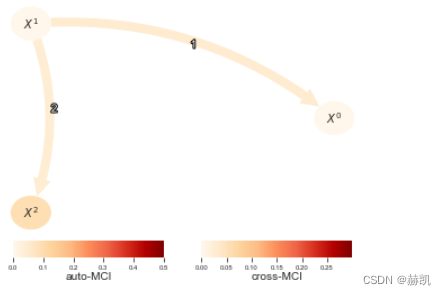
在这里,我们关注Gsquared。请注意,G2统计量值随样本量的大小而变化,但它与条件互信息相关,相关公式为 G = 2 n C M I G = 2nCMI G=2nCMI。其中, n n n是样本量。因此,我们在这里转换val_matrix以获得更好解释(和可绘图的)量。
gsquared = Gsquared(significance='analytic')
pcmci_cmi_symb = PCMCI(dataframe=dataframe, cond_ind_test=gsquared)
results = pcmci_cmi_symb.run_pcmci(tau_min = 1, tau_max=2, pc_alpha=0.2, alpha_level = 0.01)val_matrix = results['val_matrix']
val_matrix /= (2.*T)
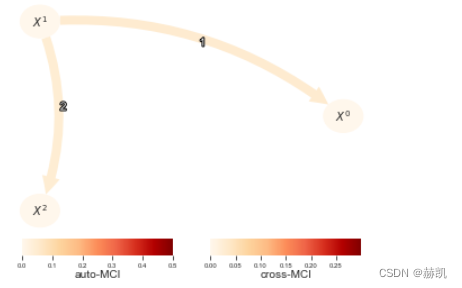
tp.plot_graph(val_matrix=val_matrix,graph=results['graph'],var_names=var_names,link_colorbar_label='cross-MCI',node_colorbar_label='auto-MCI',vmin_edges=0.,vmax_edges = 0.3,edge_ticks=0.05,cmap_edges='OrRd',vmin_nodes=0,vmax_nodes=.5,node_ticks=.1,cmap_nodes='OrRd',); plt.show()
请参考关于CMIsymb的独立教程,以及CMIknnMixed,该教程讨论了如何处理(连续和分类变量的)组合,甚至是同时包含两种类型的变量。
在这里,CMIsymb需要更长的时间并且给出了相同的结果,但对于较小的样本量和更高维度的条件集(和/或更多的分类值),Gsquared的渐近空模型分布可能不再有效,这时更倾向于使用CMIsymb。
# cmi_symb = CMIsymb(significance='shuffle_test')
# pcmci_cmi_symb = PCMCI(
# dataframe=dataframe,
# cond_ind_test=cmi_symb)
# results = pcmci_cmi_symb.run_pcmci(tau_min = 1, tau_max=2, pc_alpha=0.2, alpha_level = 0.01)
# tp.plot_graph(
# val_matrix=val_matrix,
# graph=results['graph'],
# var_names=var_names,
# link_colorbar_label='cross-MCI',
# node_colorbar_label='auto-MCI',
# vmin_edges=0.,
# vmax_edges = 0.3,
# edge_ticks=0.05,
# cmap_edges='OrRd',
# vmin_nodes=0,
# vmax_nodes=.5,
# node_ticks=.1,
# cmap_nodes='OrRd',
# ); plt.show()
2b. 混合分类/连续时间序列
通常,人们可能会遇到一种情况,即在数据集中,一些变量是分类的,而另一些是连续的。这种情况可以通过RegressionCI独立性测试来解决。然后,必须通过dataframe的data_type参数为每个变量设置类型。这里更一般地将其实现为与数据形状相同的二进制数据数组,描述变量中的个别样本(或所有样本)是连续的还是离散的:连续变量用0表示,离散变量用1表示。在这里,一个变量的所有样本必须是相同的类型。
# Generate some mixed-type data with a binary variable (can also be multinomial) causing two continuous ones.
random_state = np.random.default_rng(42)
T = 1000
data = np.zeros((T, 3))
data[:, 1] = random_state.binomial(n=1, p=0.5, size=T)
for t in range(2, T):data[t, 0] = 0.5 * data[t-1, 0] + random_state.normal(0.2 + data[t-1, 1] * 0.6, 1)data[t, 2] = 0.4 * data[t-1, 2] + random_state.normal(0.2 + data[t-2, 1] * 0.6, 1)data_type = np.zeros(data.shape, dtype='int')
# X0 is continuous, encoded as 0 in data_type
data_type[:,0] = 0
# X1 is discrete, encoded as 1 in data_type
data_type[:,1] = 1
# X2 is continuous, encoded as 0 in data_type
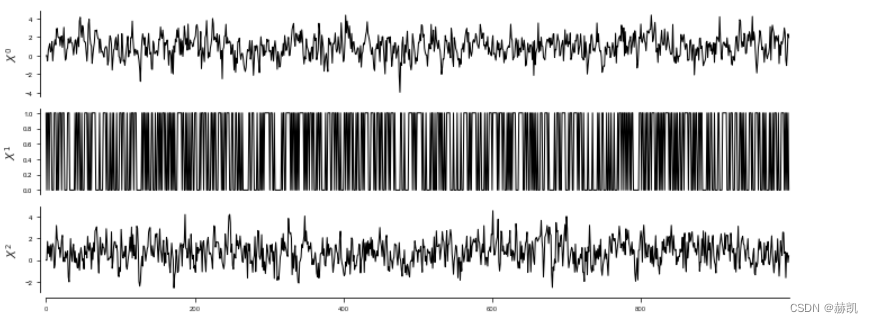
data_type[:,2] = 0dataframe = pp.DataFrame(data,data_type=data_type,var_names=var_names)
tp.plot_timeseries(dataframe, figsize=(10,4)); plt.show()
regressionCI = RegressionCI(significance='analytic')pcmci = PCMCI(dataframe=dataframe, cond_ind_test=regressionCI)
results = pcmci.run_pcmci(tau_min = 1, tau_max=2, pc_alpha=0.2, alpha_level = 0.01)# Also here the test statistic values are not very useful
val_matrix = results['val_matrix']
val_matrix /= (2.*T)
tp.plot_graph(val_matrix=val_matrix,graph=results['graph'],var_names=var_names,link_colorbar_label='cross-MCI',node_colorbar_label='auto-MCI',vmin_edges=0.,vmax_edges = 0.1,edge_ticks=0.05,cmap_edges='OrRd',vmin_nodes=0,vmax_nodes=.5,node_ticks=.1,cmap_nodes='OrRd',); plt.show()
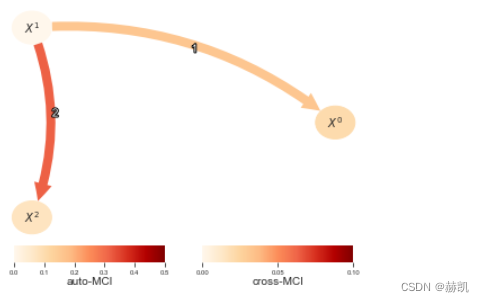
多变量X和Y的测试
上述测试中的几个也适用于多变量X和Y(所有测试都适用于多变量Z)。此外,元类PairwiseMultCI允许将每个单变量测试转换为多变量测试。该类还允许增加条件集,这可以帮助增加效应大小。
查看相应的教程和论文:
Tom Hochsprung, Jonas Wahl*, Andreas Gerhardus*, Urmi Ninad*, 和 Jakob Runge. 增加随机向量间成对条件独立测试的效应大小。UAI2023, 2023。
相关文章:

tigramite教程(七)使用TIGRAMITE 进行条件独立性测试
文章目录 概述1 连续数值变量1.1 ParCorr 偏相关(ParCorr类)1.2 鲁棒偏相关(RobustParCorr)非线性检验1.3 GPDC1.4 CMIknn 2a. 分类/符号时间序列2b. 混合分类/连续时间序列多变量X和Y的测试 概述 这个表格概述了 X ⊥ Y ∣ Z X\…...
设置)
【DevOps工具篇】使用Ansible部署Keycloak oauth2proxy 和 单点登录(SSO)设置
【DevOps工具篇】使用Ansible部署Keycloak oauth2proxy 和 单点登录(SSO)设置 目录 【DevOps工具篇】使用Ansible部署Keycloak oauth2proxy 和 单点登录(SSO)设置Ansible 基础知识部署 Keycloak创建 OIDC-客户端创建 oauth2proxy 部署顶级 Ansible PlaybookHost.iniplayboo…...

鸿蒙OS开发实例:【应用状态变量共享】
平时在开发的过程中,我们会在应用中共享数据,在不同的页面间共享信息。虽然常用的共享信息,也可以通过不同页面中组件间信息共享的方式,但有时使用应用级别的状态管理会让开发工作变得简单。 根据不同的使用场景,ArkT…...
C#清空窗体的背景图片
目录 一、涉及到的知识点 1.设置窗体的背景图 2.加载窗体背景图 3.清空窗体的背景图 二、 示例 一、涉及到的知识点 1.设置窗体的背景图 详见本文作者的其他文章:C#手动改变自制窗体的大小-CSDN博客 https://wenchm.blog.csdn.net/article/details/137027140…...
Qt 实现的万能采集库( 屏幕/相机/扬声器/麦克风采集)
【写在前面】 之前应公司需要,给公司写过一整套直播的库( 推拉流,编解码),类似于 libobs。 结果后来因为没有相关项目,便停止开发&维护了。 不过里面很多有用的组件,然后也挺好用的,遂开源出来一部分。…...

将写好的打印机代码打包成jar包然后直接注册成windows服务,然后通过调用插件的接口地址将流传到接口实现解析并无需预览直接通过打印机直接打印PDF文件
实现文件流PDF不需要预览直接调用打印机打印实现方案就是,将写好的打印机代码打包成jar包然后直接注册成windows服务,然后通过调用插件的接口地址将流传到接口实现解析并无需预览直接通过打印机直接打印PDF文件。源码地址...
加密软件VMProtect教程:使用脚本-功能
VMProtect是新一代软件保护实用程序。VMProtect支持德尔菲、Borland C Builder、Visual C/C、Visual Basic(本机)、Virtual Pascal和XCode编译器。 同时,VMProtect有一个内置的反汇编程序,可以与Windows和Mac OS X可执行文件一起…...

51单片机入门_江协科技_21.1_开发板USB口连接建议
1. 目前我自己用的普中A2版本的开发板,操作失误导致在开发板连接电脑并通电的情况下误将跳线帽触碰到开发板的3.3V与GND,导致USB口浪涌,2个电脑上面的USB口烧毁,开发板暂时没有任何问题,电脑USB口现在只是接通后有电&a…...
基于Spring Boot 3 + Spring Security6 + JWT + Redis实现登录、token身份认证
基于Spring Boot3实现Spring Security6 JWT Redis实现登录、token身份认证。 用户从数据库中获取。使用RESTFul风格的APi进行登录。使用JWT生成token。使用Redis进行登录过期判断。所有的工具类和数据结构在源码中都有。 系列文章指路👉 系列文章-基于SpringBoot3…...

Kubernetes(k8s):精通 Pod 操作的关键命令
Kubernetes(k8s):精通 Pod 操作的关键命令 1、查看 Pod 列表2、 查看 Pod 的详细信息3、创建 Pod4、删除 Pod5、获取 Pod 日志6、进入 Pod 执行命令7、暂停和启动 Pod8、改变 Pod 副本数量9、查看当前部署中使用的镜像版本10、滚动更新 Pod11…...

【随笔】Git 高级篇 -- 相对引用2(十三)
💌 所属专栏:【Git】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! 💖 欢迎大…...
xilinx AXI CAN驱动开发
CAN收发方案有很多,常见的解决方案通过是采用CAN收发芯片,例如最常用的SJA1000,xilinx直接将CAN协议栈用纯逻辑实现,AXI CAN是其中一种; 通过这种方式硬件上只需外接一个PHY芯片即可 上图加了一个电平转换芯片 软件设计方面&…...
Python:百度AI开放平台——OCR图像文字识别应用
一、注册百度AI开放平台 使用百度AI服务的步骤为: 注册:注册成为百度AI开放平台开发者;创建AI应用:在百度API开放平台上创建相关类型的的AI应用,获得AppID、API Key和Secret Key;调用API:调用…...

OpenEuler/Centos制作离线软件源
需求背景: 一般线上服务器都是不能连接外网,服务器安装好系统之后就需要部署相关软件,此时因为无法联网导致无法下载软件,所以都会做一个本地的离线软件源,本文简单介绍如何快速利用已经下载好的rpm包,制作…...

论文笔记:基于多粒度信息融合的社交媒体多模态假新闻检测
整理了ICMR2023 Multi-modal Fake News Detection on Social Media via Multi-grained Information Fusion)论文的阅读笔记 背景模型实验 背景 在假新闻检测领域,目前的方法主要集中在文本和视觉特征的集成上,但不能有效地利用细粒度和粗粒度…...
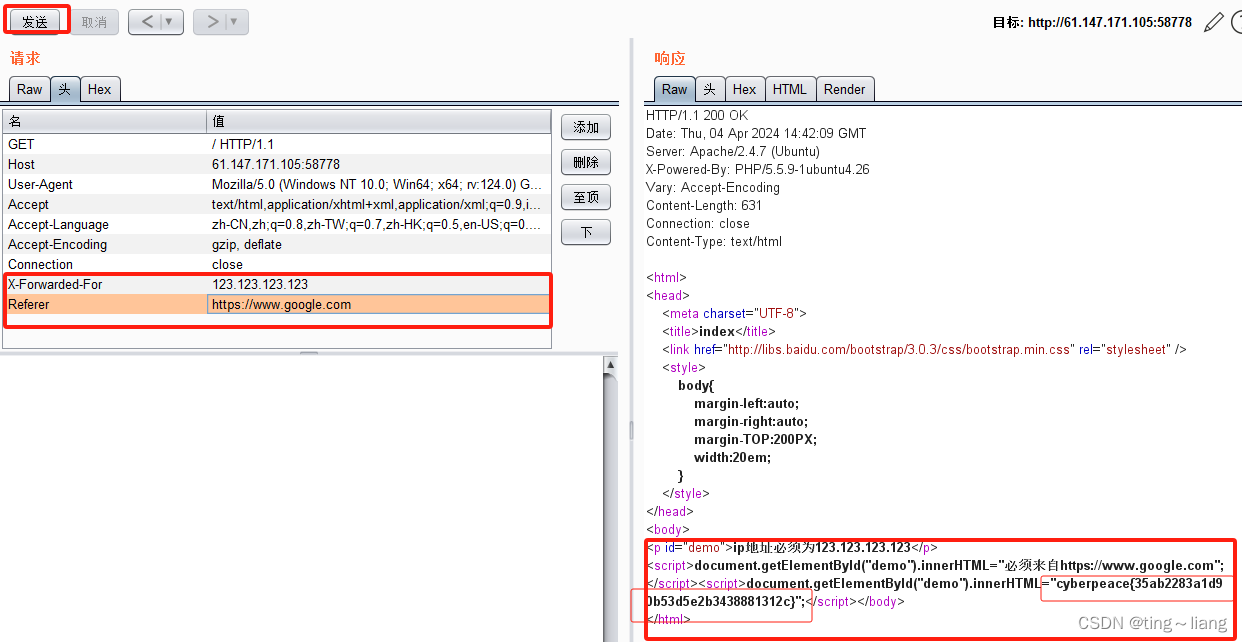
攻防世界 xff_referer 题目解析
xff_referer 一:了解xxf和Referer X-Forwarded-For:简称XFF头,它代表客户端,也就是HTTP的请求端真实的IP,只有在通过了HTTP 代理或者负载均衡服务器时才会添加该项。 一般的客户端发送HTTP请求没有X-Forwarded-For头的࿰…...
open-cd框架调试记录
源于论文Changer: Feature Interaction Is What You Need forChange Detection 源码位置:open-cd/README.md at main likyoo/open-cd (github.com) 同样是基于MMSegmentation框架的代码,不符合本人编程习惯所以一直也没有研究这东西,近期打…...

【算法刷题day17】Leetcode:110.平衡二叉树、257. 二叉树的所有路径、404.左叶子之和
文章目录 Leetcode 110.平衡二叉树解题思路代码总结 Leetcode 257. 二叉树的所有路径解题思路代码总结 Leetcode 404.左叶子之和解题思路代码总结 草稿图网站 java的Deque Leetcode 110.平衡二叉树 题目:** 110.平衡二叉树** 解析:代码随想录解析 解题思…...
Linux云计算之Linux基础2——Linux发行版本的安装
目录 一、彻底删除VMware 二、VMware-17虚拟机安装 三、MobaXterm 安装 四、Centos 发行版 7.9的安装 五、rockys 9.1的安装 六、ubuntu2204的安装 一、彻底删除VMware 在卸载VMware虚拟机之前,要先把与VMware相关的服务和进程终止 1. 在windows中按下【Windo…...

C++:赋值运算符(17)
赋值也就是将后面的值赋值给变量,这里最常用的就是 ,a1那么a就是1,此外还包含以下的赋值运算 等于int a 1; a10 a10加等于int a 1; a1;a2-减等于int a 1; a-1;a0*乘等于int a 2; a*5;a10/除等于int a 10; a/2;a5%模等于int a 10; a%…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
