数据结构和算法:十大排序
排序算法
排序算法用于对一组数据按照特定顺序进行排列。排序算法有着广泛的应用,因为有序数据通常能够被更高效地查找、分析和处理。
排序算法中的数据类型可以是整数、浮点数、字符或字符串等。排序的判断规则可根据需求设定,如数字大小、字符 ASCII 码顺序或自定义规则。
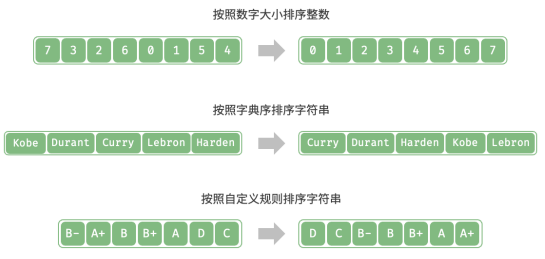
评价维度
运行效率: 期望排序算法的时间复杂度尽量低,且总体操作数量较少(时间复杂度中的常数项变小)。对于大数据量的情况,运行效率显得尤为重要。
就地性: 顾名思义,原地排序通过在原数组上直接操作实现排序,无须借助额外的辅助数组,从而节省内存。通常情况下,原地排序的数据搬运操作较少,运行速度也更快。
稳定性: 稳定排序在完成排序后,相等元素在数组中的相对顺序不发生改变。
稳定排序是多级排序场景的必要条件。
自适应性: 自适应排序的时间复杂度会受输入数据的影响,即最佳时间复杂度、最差时间复杂度、平均时间复杂度并不完全相等。
自适应性需要根据具体情况来评估。如果最差时间复杂度差于平均时间复杂度,说明排序算法在某些数据下性能可能劣化,因此被视为负面属性;而如果最佳时间复杂度优于平均时间复杂度,则被视为正面属性。
是否基于比较: 基于比较的排序依赖比较运算符(<、=、>)来判断元素的相对顺序,从而排序整个数
组,理论最优时间复杂度为 𝑂(𝑛 log 𝑛) 。而非比较排序不使用比较运算符,时间复杂度可达 𝑂(𝑛) ,但其通用性相对较差。
理想排序算法
运行快、原地、稳定、正向自适应、通用性好。显然,迄今为止尚未发现兼具以上所有特性的排序算法。因此,在选择排序算法时,需要根据具体的数据特点和问题需求来决定。
选择排序
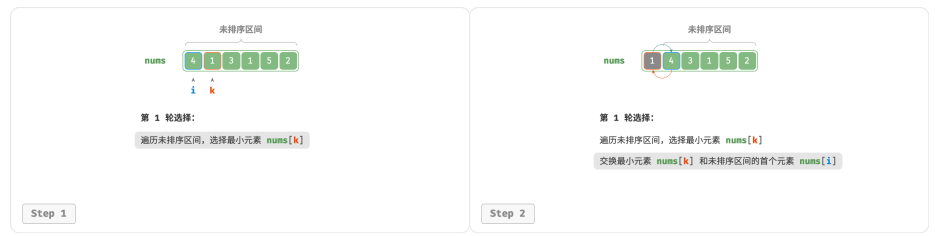
选择排序(selection sort)的工作原理:开启一个循环,每轮从未排序区间选择最小的元素,将其放到已排序区间的末尾。
设数组的长度为 𝑛 ,选择排序的算法流程如图:
1.初始状态下,所有元素未排序,即未排序(索引)区间为 [0, 𝑛 − 1] 。
2.选取区间 [0, 𝑛 − 1] 中的最小元素,将其与索引 0 处的元素交换。完成后,数组前 1 个元素已排序。
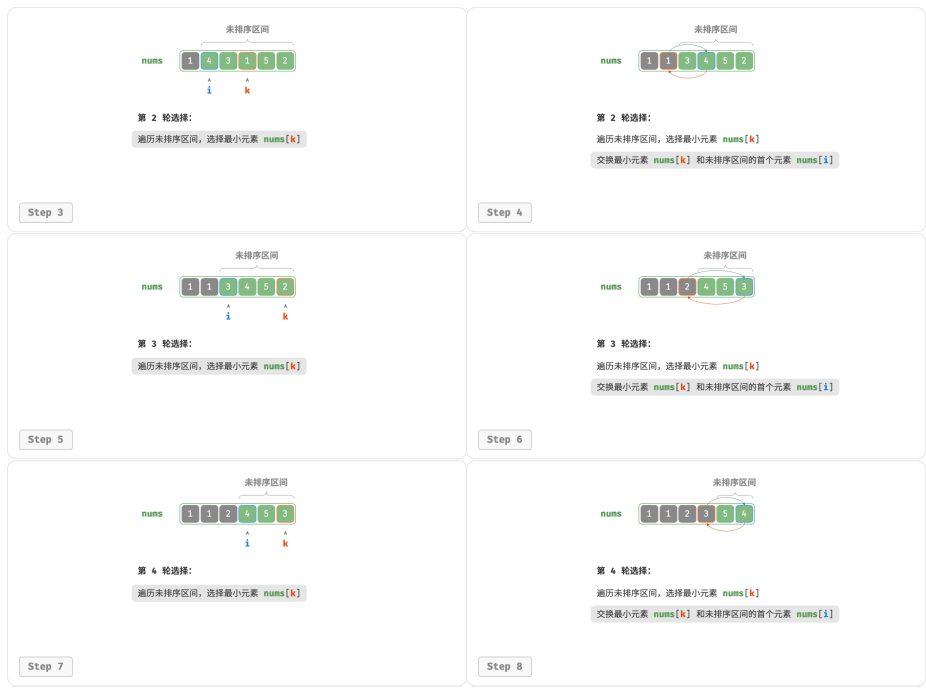
3.选取区间 [1, 𝑛 − 1] 中的最小元素,将其与索引 1 处的元素交换。完成后,数组前 2 个元素已排序。
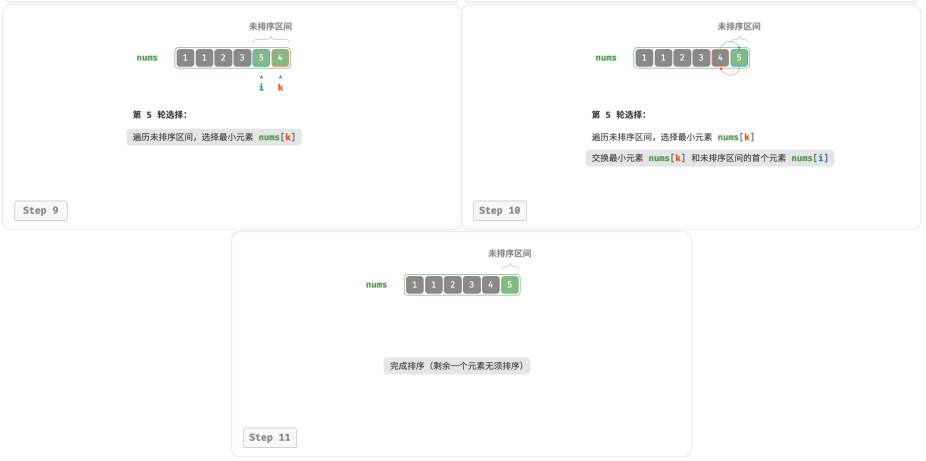
4. 以此类推。经过 𝑛 − 1 轮选择与交换后,数组前 𝑛 − 1 个元素已排序。
5. 仅剩的一个元素必定是最大元素,无须排序,因此数组排序完成
/* 选择排序 */
void selectionSort(vector<int> &nums) {int n = nums.size();// 外循环:未排序区间为 [i, n-1]for (int i = 0; i < n - 1; i++) {// 内循环:找到未排序区间内的最小元素int k = i;for (int j = i + 1; j < n; j++) {if (nums[j] < nums[k])k = j; // 记录最小元素的索引}// 将该最小元素与未排序区间的首个元素交换swap(nums[i], nums[k]);}
}
时间复杂度为 𝑂(𝑛^2)、非自适应排序:外循环共 𝑛 − 1 轮,第一轮的未排序区间长度为 𝑛 ,最后一轮的未排序区间长度为 2 ,即各轮外循环分别包含 𝑛、𝑛 − 1、…、3、2 轮内循环,求和为 ((𝑛−1)(𝑛+2))/2 。
空间复杂度为 𝑂(1)、原地排序:指针 𝑖 和 𝑗 使用常数大小的额外空间。
非稳定排序:如图所示,元素 nums[i] 有可能被交换至与其相等的元素的右边,导致两者的相对顺序发生改变。
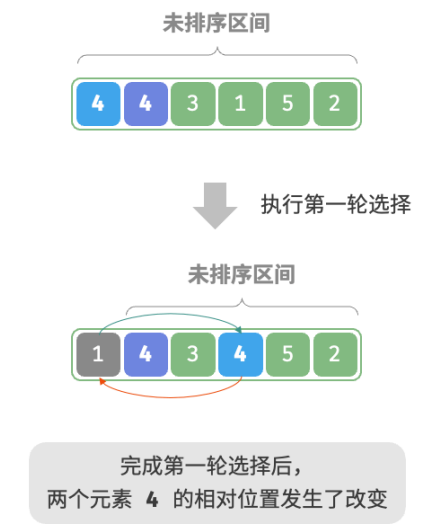
冒泡排序
冒泡排序(bubble sort)通过连续地比较与交换相邻元素实现排序。这个过程就像气泡从底部升到顶部一样,因此得名冒泡排序。
冒泡过程可以利用元素交换操作来模拟:从数组最左端开始向右遍历,依次比较相邻元素大小,如果“左元素 > 右元素”就交换二者。遍历完成后,最大的元素会被移动到数组的最右端。

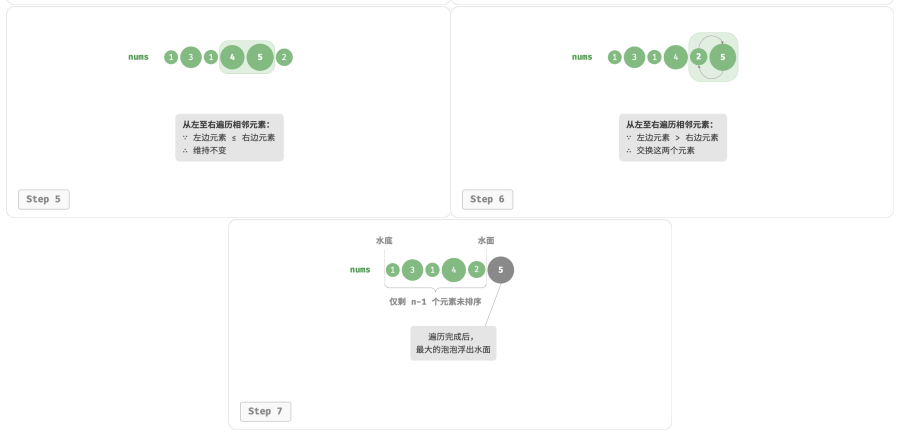
算法流程:
1.首先,对 𝑛 个元素执行“冒泡”,将数组的最大元素交换至正确位置;
2.接下来,对剩余 𝑛 − 1 个元素执行“冒泡”,将第二大元素交换至正确位置;
3.以此类推,经过 𝑛 − 1 轮“冒泡”后,前 𝑛 − 1 大的元素都被交换至正确位置;
4.仅剩的一个元素必定是最小元素,无须排序,因此数组排序完成。

/* 冒泡排序 */
void bubbleSort(vector<int> &nums) {// 外循环:未排序区间为 [0, i]for (int i = nums.size() - 1; i > 0; i--) {// 内循环:将未排序区间 [0, i] 中的最大元素交换至该区间的最右端for (int j = 0; j < i; j++) {if (nums[j] > nums[j + 1]) {// 交换 nums[j] 与 nums[j + 1]// 这里使用了 std::swap() 函数swap(nums[j], nums[j + 1]);}}}
}
效率优化:如果某轮“冒泡”中没有执行任何交换操作,说明数组已经完成排序,可直接返回结果。
增加一个标志位 flag 来监测这种情况,一旦出现就立即返回,冒泡排序的最差时间复杂度和平均时间复杂度仍为 𝑂(𝑛^2) ;但当输入数组完全有序时,可达到最佳时间复杂度 𝑂(𝑛)。
/* 冒泡排序(标志优化)*/
void bubbleSortWithFlag(vector<int> &nums) {// 外循环:未排序区间为 [0, i]for (int i = nums.size() - 1; i > 0; i--) {bool flag = false; // 初始化标志位// 内循环:将未排序区间 [0, i] 中的最大元素交换至该区间的最右端for (int j = 0; j < i; j++) {if (nums[j] > nums[j + 1]) {// 交换 nums[j] 与 nums[j + 1]// 这里使用了 std::swap() 函数swap(nums[j], nums[j + 1]);flag = true; // 记录交换元素cout<<"swap: "<<nums[j]<<" <-> "<<nums[j+1]<<endl;}}if (!flag)break; // 此轮“冒泡”未交换任何元素,直接跳出}
}
时间复杂度为 𝑂(𝑛^2)、自适应排序:各轮“冒泡”遍历的数组长度依次为 𝑛 − 1、𝑛 − 2、…、2、1 ,总和为 (𝑛 − 1)𝑛/2 。在引入 flag 优化后,最佳时间复杂度可达到 𝑂(𝑛) 。
空间复杂度为 𝑂(1)、原地排序:指针 𝑖 和 𝑗 使用常数大小的额外空间。
稳定排序:由于在“冒泡”中遇到相等元素不交换。
插入排序
插入排序(insertion sort)是一种简单的排序算法,在未排序区间选择一个基准元素,将该元素与其左侧已排序区间的元素逐一比较大小,并将该元素插入到正确的位置。
设基准元素为 base ,需要将从目标索引到 base 之间的所有元素向右移动一位,然后将 base 赋值给目标索引。
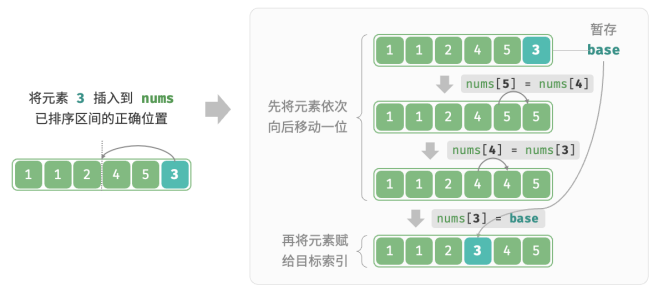
算法流程:
1.初始状态下,数组的第 1 个元素已完成排序。
2.选取数组的第 2 个元素作为 base ,将其插入到正确位置后,数组的前 2 个元素已排序。
3.选取第 3 个元素作为 base ,将其插入到正确位置后,数组的前 3 个元素已排序。
4.以此类推,在最后一轮中,选取最后一个元素作为 base ,将其插入到正确位置后,所有元素均已排序
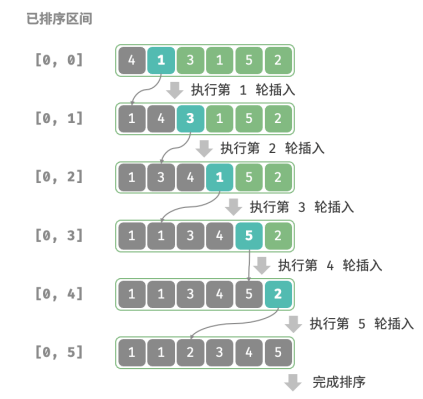
/* 插入排序 */
void insertionSort(vector<int> &nums) {// 外循环:已排序元素数量为 1, 2, ..., nfor (int i = 1; i < nums.size(); i++) {int base = nums[i], j = i - 1;// 内循环:将 base 插入到已排序部分的正确位置while (j >= 0 && nums[j] > base) {nums[j + 1] = nums[j]; // 将 nums[j] 向右移动一位j--;}nums[j + 1] = base; // 将 base 赋值到正确位置 num[0]-->j=-1// cout<<base<<endl;}
}
算法特性:
时间复杂度为 𝑂(𝑛^2)、自适应排序:在最差情况下,每次插入操作分别需要循环 𝑛 − 1、𝑛 − 2、…、2、1 次,求和得到 (𝑛 − 1)𝑛/2 ,因此时间复杂度为 𝑂(𝑛 ^2) 。在遇到有序数据时,插入操作会提前终止。当输入数组完全有序时,插入排序达到最佳时间复杂度 𝑂(𝑛) 。
空间复杂度为 𝑂(1)、原地排序:指针 𝑖 和 𝑗 使用常数大小的额外空间。
稳定排序:在插入操作过程中,会将元素插入到相等元素的右侧,不会改变它们的顺序。
插入排序的优势
插入排序的时间复杂度为 𝑂(𝑛^2) ,而快速排序的时间复杂度为 𝑂(𝑛 log 𝑛) 。尽管插入排序的时间复杂度更高,但在数据量较小的情况下,插入排序通常更快。
这个结论与线性查找和二分查找的适用情况的结论类似。快速排序这类 𝑂(𝑛 log 𝑛) 的算法属于基于分治策略的排序算法,往往包含更多单元计算操作。而在数据量较小时,𝑛^2 和 𝑛 log 𝑛 的数值比较接近,复杂度不占主导地位,每轮中的单元操作数量起到决定性作用。
虽然冒泡排序、选择排序和插入排序的时间复杂度都为 𝑂(𝑛 ^2) ,但在实际情况中,插入排序的使用频率显著高于冒泡排序和选择排序,主要有以下原因:
1.冒泡排序基于元素交换实现,需要借助一个临时变量,共涉及 3 个单元操作;插入排序基于元素赋值实现,仅需 1 个单元操作。因此,冒泡排序的计算开销通常比插入排序更高;
2.选择排序在任何情况下的时间复杂度都为 𝑂(𝑛^2) 。如果给定一组部分有序的数据,插入排序通常比选
择排序效率更高。
3.选择排序不稳定,无法应用于多级排序。
快速排序
快速排序(quick sort)是一种基于分治策略的排序算法,运行高效,应用广泛。
快速排序的核心操作是“哨兵划分”,其目标是:选择数组中的某个元素作为“基准数”,将所有小于基准数的元素移到其左侧,而大于基准数的元素移到其右侧。
具体来说,哨兵划分的流程如图所示:

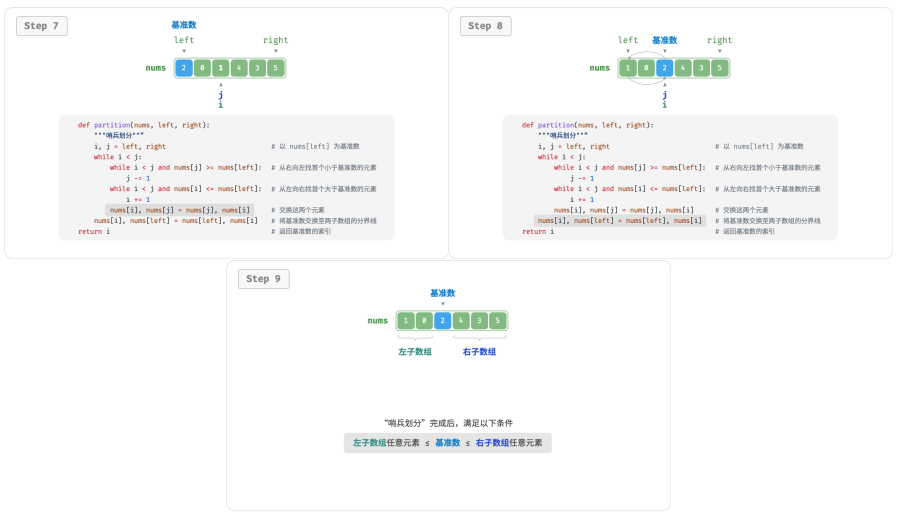
- 选取数组最左端元素作为基准数,初始化两个指针 i 和 j 分别指向数组的两端。
- 设置一个循环,在每轮中使用 i(j)分别寻找第一个比基准数大(小)的元素,然后交换这两个元素。
- 循环执行步骤 2. ,直到 i 和 j 相遇时停止,最后将基准数交换至两个子数组的分界线。
哨兵划分完成后,原数组被划分成三部分:左子数组、基准数、右子数组,且满足“左子数组任意元素 ≤ 基准数 ≤ 右子数组任意元素”。因此,我们接下来只需对这两个子数组进行排序。
/* 元素交换 */
static void swap(vector<int> &nums, int i, int j) {int tmp = nums[i];nums[i] = nums[j];nums[j] = tmp;
}/* 哨兵划分 */
static int partition(vector<int> &nums, int left, int right) {// 以 nums[left] 为基准数int i = left, j = right;while (i < j) {while (i < j && nums[j] >= nums[left])j--; // 从右向左找首个小于基准数的元素while (i < j && nums[i] <= nums[left])i++; // 从左向右找首个大于基准数的元素swap(nums, i, j); // 交换这两个元素}swap(nums, i, left); // 将基准数交换至两子数组的分界线return i; // 返回基准数的索引
}
整体流程:
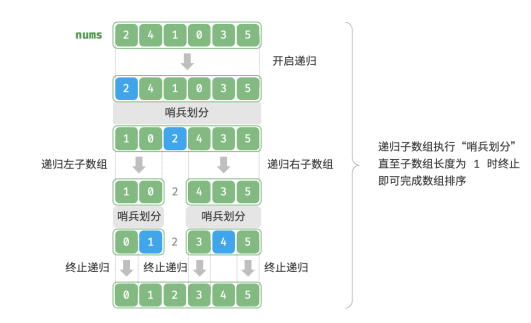
1.首先,对原数组执行一次“哨兵划分”,得到未排序的左子数组和右子数组;
2.然后,对左子数组和右子数组分别递归执行“哨兵划分”;
3.持续递归,直至子数组长度为 1 时终止,从而完成整个数组的排序;
/* 快速排序(尾递归优化) */
static void quickSort(vector<int> &nums, int left, int right) {// 子数组长度为 1 时终止while (left < right) {// 哨兵划分操作int pivot = partition(nums, left, right);// 对两个子数组中较短的那个执行快速排序if (pivot - left < right - pivot) {quickSort(nums, left, pivot - 1); // 递归排序左子数组left = pivot + 1; // 剩余未排序区间为 [pivot + 1, right]} else {quickSort(nums, pivot + 1, right); // 递归排序右子数组right = pivot - 1; // 剩余未排序区间为 [left, pivot - 1]}}
}
时间复杂度为 𝑂(𝑛 log 𝑛)、自适应排序:在平均情况下,哨兵划分的递归层数为 log 𝑛 ,每层中的总循环数为 𝑛 ,总体使用 𝑂(𝑛 log 𝑛) 时间。在最差情况下,每轮哨兵划分操作都将长度为 𝑛 的数组划分为长度为 0 和 𝑛−1 的两个子数组,此时递归层数达到 𝑛 ,每层中的循环数为 𝑛 ,总体使用 𝑂(𝑛^2) 时间。
空间复杂度为 𝑂(𝑛)、原地排序:在输入数组完全倒序的情况下,达到最差递归深度 𝑛 ,使用 𝑂(𝑛) 栈帧空间。排序操作是在原数组上进行的,未借助额外数组。
非稳定排序:在哨兵划分的最后一步,基准数可能会被交换至相等元素的右侧。
快速排序为什么快
尽管快速排序的平均时间复杂度与“归并排序”和“堆排序”相同,但通常快速排序的效率更高,主要有以下原因:
1.出现最差情况的概率很低:虽然快速排序的最差时间复杂度为 𝑂(𝑛^2) ,没有归并排序稳定,但在绝大多数情况下,快速排序能在 𝑂(𝑛 log 𝑛) 的时间复杂度下运行。
2.缓存使用效率高:在执行哨兵划分操作时,系统可将整个子数组加载到缓存,因此访问元素的效率较
高。而像“堆排序”这类算法需要跳跃式访问元素,从而缺乏这一特性。
3. 复杂度的常数系数小:快速排序的比较、赋值、交换等操作的总数量最少。这与“插入排序”比“冒泡排序”更快的原因类似。
基准数优化
快速排序在某些输入下的时间效率可能降低。
极端例子:假设输入数组是完全倒序的,由于选择最左端元素作为基准数,那么在哨兵划分完成后,基准数被交换至数组最右端,导致左子数组长度为 𝑛 − 1、右子数组长度为 0 。如此递归下去,每轮哨兵划分后都有一个子数组的长度为 0 ,分治策略失效,快速排序退化为“冒泡排序”的近似形式。
为了尽量避免这种情况发生,可以优化哨兵划分中的基准数的选取策略。例如,可以随机选取一个元素作为基准数。然而,如果运气不佳,每次都选到不理想的基准数,效率仍然不尽如人意。
为了进一步改进,可以在数组中选取三个候选元素(通常为数组的首、尾、中点元素),并将这三个候选元素的中位数作为基准数。这样一来,基准数“既不太小也不太大”的概率将大幅提升。当然,还可以选取更多候选元素,以进一步提高算法的稳健性。采用这种方法后,时间复杂度劣化至 𝑂(𝑛^2) 的概率大大降低。
/* 哨兵划分(三数取中值) */
static int partition(vector<int> &nums, int left, int right) {// 选取三个候选元素的中位数int med = medianThree(nums, left, (left + right) / 2, right);// 将中位数交换至数组最左端swap(nums, left, med);// 以 nums[left] 为基准数int i = left, j = right;while (i < j) {while (i < j && nums[j] >= nums[left])j--; // 从右向左找首个小于基准数的元素while (i < j && nums[i] <= nums[left])i++; // 从左向右找首个大于基准数的元素swap(nums, i, j); // 交换这两个元素}swap(nums, i, left); // 将基准数交换至两子数组的分界线return i; // 返回基准数的索引
}
尾递归优化
在某些输入下,快速排序可能占用空间较多。以完全有序的输入数组为例,设递归中的子数组长度为 𝑚 ,每轮哨兵划分操作都将产生长度为 0 的左子数组和长度为 𝑚 − 1 的右子数组,这意味着每一层递归调用减少的问题规模非常小(只减少一个元素),递归树的高度会达到 𝑛−1 ,此时需要占用 𝑂(𝑛) 大小的栈帧空间。
为了防止栈帧空间的累积,可以在每轮哨兵排序完成后,比较两个子数组的长度,仅对较短的子数组进行递归。
由于较短子数组的长度不会超过 𝑛/2 ,因此这种方法能确保递归深度不超过 log 𝑛 ,从而将最差空间复杂度优化至 𝑂(log 𝑛) 。代码如下所示:
/* 快速排序(尾递归优化) */
static void quickSort(vector<int> &nums, int left, int right) {// 子数组长度为 1 时终止while (left < right) {// 哨兵划分操作int pivot = partition(nums, left, right);// 对两个子数组中较短的那个执行快速排序if (pivot - left < right - pivot) {quickSort(nums, left, pivot - 1); // 递归排序左子数组left = pivot + 1; // 剩余未排序区间为 [pivot + 1, right]} else {quickSort(nums, pivot + 1, right); // 递归排序右子数组right = pivot - 1; // 剩余未排序区间为 [left, pivot - 1]}}
}
归并排序
归并排序(merge sort)是一种基于分治策略的排序算法,包含“划分”和“合并”阶段。
1.划分阶段:通过递归不断地将数组从中点处分开,将长数组的排序问题转换为短数组的排序问题。
2.合并阶段:当子数组长度为 1 时终止划分,开始合并,持续地将左右两个较短的有序数组合并为一个较长的有序数组,直至结束。
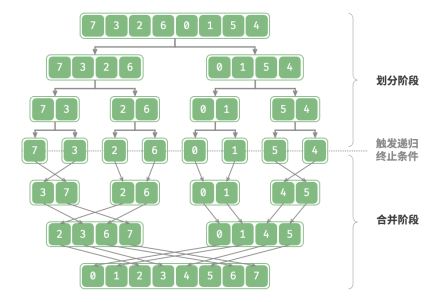
“划分阶段” 从顶至底递归地将数组从中点切分为两个子数组。
1.计算数组中点 mid ,递归划分左子数组(区间 [left, mid] )和右子数组(区间 [mid + 1, right] )。
2.递归执行步骤 1. ,直至子数组区间长度为 1 时终止。
“合并阶段” 从底至顶地将左子数组和右子数组合并为一个有序数组。需要注意的是,从长度为 1 的子数组开始合并,合并阶段中的每个子数组都是有序的。
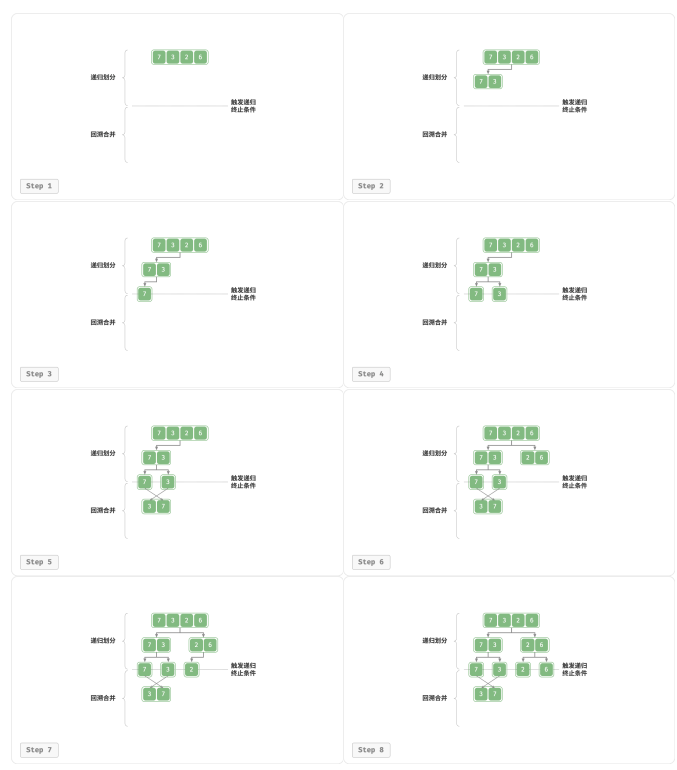

观察发现,归并排序与二叉树后序遍历的递归顺序是一致的:
后序遍历:先递归左子树,再递归右子树,最后处理根节点。
归并排序:先递归左子数组,再递归右子数组,最后处理合并。
归并排序的实现如以下代码所示。请注意,nums 的待合并区间为 [left, right] ,而 tmp 的对应区间为 [0, right - left] 。
/* 合并左子数组和右子数组 */
void merge(vector<int> &nums, int left, int mid, int right) {// 左子数组区间为 [left, mid], 右子数组区间为 [mid+1, right]// 创建一个临时数组 tmp ,用于存放合并后的结果vector<int> tmp(right - left + 1);// 初始化左子数组和右子数组的起始索引int i = left, j = mid + 1, k = 0;// 当左右子数组都还有元素时,进行比较并将较小的元素复制到临时数组中while (i <= mid && j <= right) {if (nums[i] <= nums[j])tmp[k++] = nums[i++];elsetmp[k++] = nums[j++];}// 将左子数组和右子数组的剩余元素复制到临时数组中while (i <= mid) {tmp[k++] = nums[i++];}while (j <= right) {tmp[k++] = nums[j++];}// 将临时数组 tmp 中的元素复制回原数组 nums 的对应区间for (k = 0; k < tmp.size(); k++) {nums[left + k] = tmp[k];}
}
时间复杂度为 𝑂(𝑛 log 𝑛)、非自适应排序:划分产生高度为 log 𝑛 的递归树,每层合并的总操作数量为 𝑛 ,因此总体时间复杂度为 𝑂(𝑛 log 𝑛) 。
空间复杂度为 𝑂(𝑛)、非原地排序:递归深度为 log 𝑛 ,使用 𝑂(log 𝑛) 大小的栈帧空间。合并操作需要借助辅助数组实现,使用 𝑂(𝑛) 大小的额外空间。
稳定排序:在合并过程中,相等元素的次序保持不变。
链表排序
对于链表,归并排序相较于其他排序算法具有显著优势,可以将链表排序任务的空间复杂度优化至 𝑂(1) 。
划分阶段:可以使用“迭代”替代“递归”来实现链表划分工作,从而省去递归使用的栈帧空间。
合并阶段:在链表中,节点增删操作仅需改变引用(指针)即可实现,因此合并阶段(将两个短有序链表合并为一个长有序链表)无须创建额外链表。
堆排序
堆排序(heap sort)是一种基于堆数据结构实现的高效排序算法。可以利用已经学过的“建堆操作”和“元素出堆操作”实现堆排序。
1.输入数组并建立小顶堆,此时最小元素位于堆顶;
2.不断执行出堆操作,依次记录出堆元素,即可得到从小到大排序的序列。
以上方法虽然可行,但需要借助一个额外数组来保存弹出的元素,比较浪费空间。
在实际中,通常使用一种更加优雅的实现方式。
算法流程
1.输入数组并建立大顶堆。完成后,最大元素位于堆顶;
2.将堆顶元素(第一个元素)与堆底元素(最后一个元素)交换。完成交换后,堆的长度减 1 ,已排序元素数量加1;
3.从堆顶元素开始,从顶到底执行堆化操作(sift down)。完成堆化后,堆的性质得到修复;
4.循环执行第 2. 步和第 3. 步。循环 𝑛 − 1 轮后,即可完成数组排序。
实际上,元素出堆操作中也包含第 2. 步和第 3. 步,只是多了一个弹出元素的步骤。


在代码实现中,使用了与“堆”相同的从顶至底堆化 sift_down() 函数。值得注意的是,由于堆的长度会随着提取最大元素而减小,因此需要给 sift_down() 函数添加一个长度参数 𝑛 ,用于指定堆的当前有效长度。代码如下所示:
/*** File: heap_sort.cpp* Created Time: 2023-05-26* Author: Krahets (krahets@163.com)*/#include "../utils/common.hpp"/* 堆的长度为 n ,从节点 i 开始,从顶至底堆化 */
void siftDown(vector<int> &nums, int n, int i) {while (true) {// 判断节点 i, l, r 中值最大的节点,记为 maint l = 2 * i + 1;int r = 2 * i + 2;int ma = i;if (l < n && nums[l] > nums[ma])ma = l;if (r < n && nums[r] > nums[ma])ma = r;// 若节点 i 最大或索引 l, r 越界,则无须继续堆化,跳出if (ma == i) {break;}// 交换两节点swap(nums[i], nums[ma]);// 循环向下堆化i = ma;}
}/* 堆排序 */
void heapSort(vector<int> &nums) {// 建堆操作:堆化除叶节点以外的其他所有节点for (int i = nums.size() / 2 - 1; i >= 0; --i) {siftDown(nums, nums.size(), i);}// 从堆中提取最大元素,循环 n-1 轮for (int i = nums.size() - 1; i > 0; --i) {// 交换根节点与最右叶节点(交换首元素与尾元素)swap(nums[0], nums[i]);// 以根节点为起点,从顶至底进行堆化siftDown(nums, i, 0);}
}/* Driver Code */
int main() {vector<int> nums = {4, 1, 3, 1, 5, 2};heapSort(nums);cout << "堆排序完成后 nums = ";printVector(nums);return 0;
}
算法特性
时间复杂度为 𝑂(𝑛 log 𝑛)、非自适应排序:建堆操作使用 𝑂(𝑛) 时间。从堆中提取最大元素的时间复杂度为 𝑂(log 𝑛) ,共循环 𝑛 − 1 轮。
空间复杂度为 𝑂(1)、原地排序:几个指针变量使用 𝑂(1) 空间。元素交换和堆化操作都是在原数组上进行的。
非稳定排序:在交换堆顶元素和堆底元素时,相等元素的相对位置可能发生变化。
桶排序
基于比较的排序算法”,它们通过比较元素间的大小来实现排序。
此类排序算法的时间复杂度无法超越 𝑂(𝑛 log 𝑛) 。
“非比较排序算法”,它们的时间复杂度可以达到线性阶。
桶排序(bucket sort)是分治策略的一个典型应用。它通过设置一些具有大小顺序的桶,每个桶对应一个数据范围,将数据平均分配到各个桶中;然后,在每个桶内部分别执行排序;最终按照桶的顺序将所有数据合并。
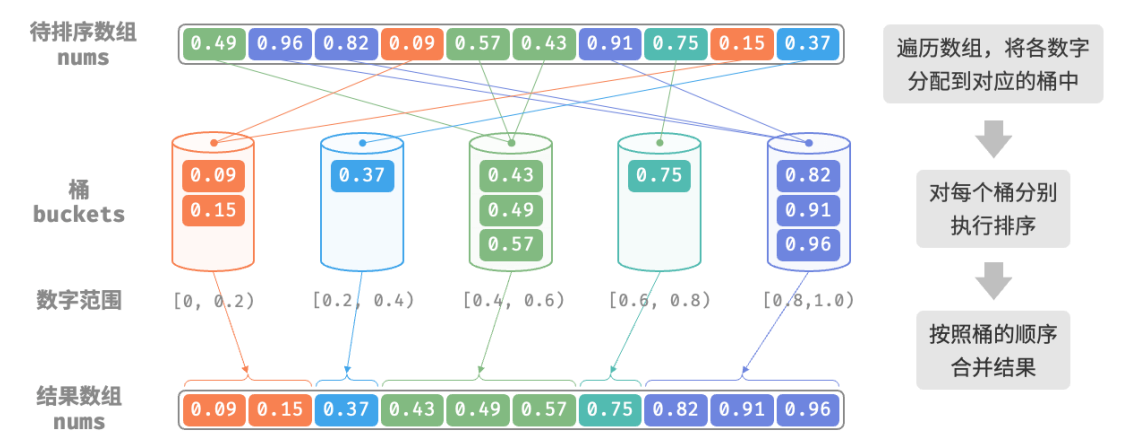
考虑一个长度为 𝑛 的数组,其元素是范围 [0, 1) 内的浮点数。
桶排序的流程如图所示:
1.初始化 𝑘 个桶,将 𝑛 个元素分配到 𝑘 个桶中。
2.对每个桶分别执行排序(这里采用编程语言的内置排序函数)。
3.按照桶从小到大的顺序合并结果。
/*** File: bucket_sort.cpp* Created Time: 2023-03-30* Author: Krahets (krahets@163.com)*/#include "../utils/common.hpp"/* 桶排序 */
void bucketSort(vector<float> &nums) {// 初始化 k = n/2 个桶,预期向每个桶分配 2 个元素int k = nums.size() / 2;vector<vector<float>> buckets(k);// 1. 将数组元素分配到各个桶中for (float num : nums) {// 输入数据范围为 [0, 1),使用 num * k 映射到索引范围 [0, k-1]int i = num * k;// 将 num 添加进桶 bucket_idxbuckets[i].push_back(num);}// 2. 对各个桶执行排序for (vector<float> &bucket : buckets) {// 使用内置排序函数,也可以替换成其他排序算法sort(bucket.begin(), bucket.end());}// 3. 遍历桶合并结果int i = 0;for (vector<float> &bucket : buckets) {for (float num : bucket) {nums[i++] = num;}}
}/* Driver Code */
int main() {// 设输入数据为浮点数,范围为 [0, 1)vector<float> nums = {0.49f, 0.96f, 0.82f, 0.09f, 0.57f, 0.43f, 0.91f, 0.75f, 0.15f, 0.37f};bucketSort(nums);cout << "桶排序完成后 nums = ";printVector(nums);return 0;
}
算法特性
桶排序适用于处理体量很大的数据。例如,输入数据包含 100 万个元素,由于空间限制,系统内存无法一次性加载所有数据。此时,可以将数据分成 1000 个桶,然后分别对每个桶进行排序,最后将结果合并。
时间复杂度为 𝑂(𝑛 + 𝑘) :假设元素在各个桶内平均分布,那么每个桶内的元素数量为 𝑛/𝑘 。
假设排序单个桶使用 𝑂( 𝑛/𝑘 log 𝑛/𝑘) 时间,则排序所有桶使用 𝑂(𝑛 log 𝑛/𝑘) 时间。当桶数量 𝑘 比较大时,时间复杂度则趋向于 𝑂(𝑛) 。合并结果时需要遍历所有桶和元素,花费 𝑂(𝑛 + 𝑘) 时间。
自适应排序:在最差情况下,所有数据被分配到一个桶中,且排序该桶使用 𝑂(𝑛^2) 时间。
空间复杂度为 𝑂(𝑛 + 𝑘)、非原地排序:需要借助 𝑘 个桶和总共 𝑛 个元素的额外空间。
桶排序是否稳定取决于排序桶内元素的算法是否稳定。
如何实现平均分配?
桶排序的时间复杂度理论上可以达到 𝑂(𝑛) ,关键在于将元素均匀分配到各个桶中,因为实际数据往往不是均匀分布的。
为实现平均分配,可以先设定一条大致的分界线,将数据粗略地分到几个桶中。分配完毕后,再将数据较多的桶继续划分为几个桶,直至所有桶中的元素数量大致相等。
可以根据数据概率分布设置每个桶的分界线。值得注意的是,数据分布并不一定需要特意统计,也可以根据数据特点采用某种概率模型进行近似。
计数排序
计数排序通过统计元素数量来实现排序,通常应用于整数数组。
给定一个长度为 𝑛 的数组 nums ,其中的元素都是“非负整数”,计数排序的整体流程:
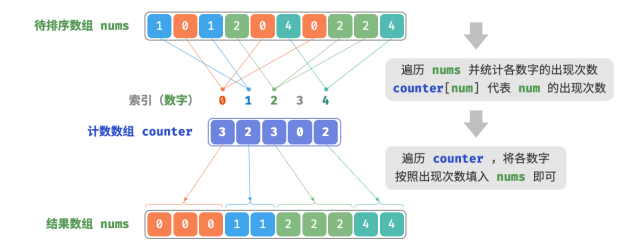
1.遍历数组,找出其中的最大数字,记为 𝑚 ,然后创建一个长度为 𝑚 + 1 的辅助数组 counter 。
2.借助 counter 统计 nums 中各数字的出现次数,其中 counter[num] 对应数字 num 的出现次数。统计方法很简单,只需遍历 nums(设当前数字为 num),每轮将 counter[num] 增加 1 即可。
3.由于 counter 的各个索引天然有序,因此相当于所有数字已经排序好了。接下来,遍历 counter ,根据各数字出现次数从小到大的顺序填入 nums 即可。
/*** File: counting_sort.cpp* Created Time: 2023-03-17* Author: Krahets (krahets@163.com)*/#include "../utils/common.hpp"/* 计数排序 */
// 简单实现,无法用于排序对象
void countingSortNaive(vector<int> &nums) {// 1. 统计数组最大元素 mint m = 0;for (int num : nums) {m = max(m, num);}// 2. 统计各数字的出现次数// counter[num] 代表 num 的出现次数vector<int> counter(m + 1, 0);for (int num : nums) {counter[num]++;}// 3. 遍历 counter ,将各元素填入原数组 numsint i = 0;for (int num = 0; num < m + 1; num++) {for (int j = 0; j < counter[num]; j++, i++) {nums[i] = num;}}
}
从桶排序的角度看,可以将计数排序中的计数数组 counter 的每个索引视为一个桶,将统计数量的过程看作将各个元素分配到对应的桶中。本质上,计数排序是桶排序在整型数据下的一个特例。
完整实现
如果输入数据是对象,上述步骤 3. 就失效了。
首先计算 counter 的“前缀和”。顾名思义,索引 i 处的前缀和 prefix[i] 等于数组前 i 个元素之和:
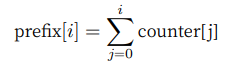
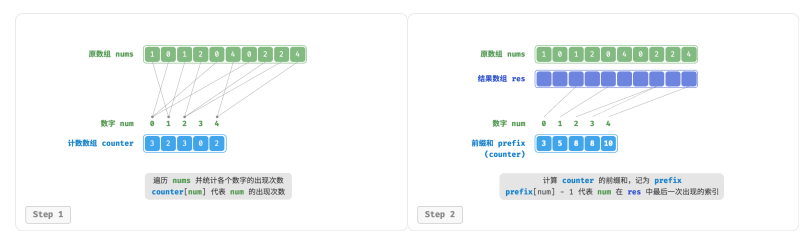
前缀和具有明确的意义,prefix[num] - 1 代表元素 num 在结果数组 res 中最后一次出现的索引。
它告诉我们各个元素应该出现在结果数组的哪个位置。接下来,我们倒序遍历原数组 nums 的每个元素 num ,在每轮迭代中执行以下两步:
1.将 num 填入数组 res 的索引 prefix[num] - 1 处。
2.令前缀和 prefix[num] 减小 1 ,从而得到下次放置 num 的索引。
遍历完成后,数组 res 中就是排序好的结果,最后使用 res 覆盖原数组 nums 即可。

/* 计数排序 */
// 完整实现,可排序对象,并且是稳定排序
void countingSort(vector<int> &nums) {// 1. 统计数组最大元素 mint m = 0;for (int num : nums) {m = max(m, num);}// 2. 统计各数字的出现次数// counter[num] 代表 num 的出现次数vector<int> counter(m + 1, 0);for (int num : nums) {counter[num]++;}// 3. 求 counter 的前缀和,将“出现次数”转换为“尾索引”// 即 counter[num]-1 是 num 在 res 中最后一次出现的索引for (int i = 0; i < m; i++) {counter[i + 1] += counter[i];}// 4. 倒序遍历 nums ,将各元素填入结果数组 res// 初始化数组 res 用于记录结果int n = nums.size();vector<int> res(n);for (int i = n - 1; i >= 0; i--) {int num = nums[i];res[counter[num] - 1] = num; // 将 num 放置到对应索引处counter[num]--; // 令前缀和自减 1 ,得到下次放置 num 的索引}// 使用结果数组 res 覆盖原数组 numsnums = res;
}算法特性
时间复杂度为 𝑂(𝑛 + 𝑚) :涉及遍历 nums 和遍历 counter ,都使用线性时间。一般情况下 𝑛 ≫ 𝑚 ,时间复杂度趋于 𝑂(𝑛) 。
空间复杂度为 𝑂(𝑛 + 𝑚)、非原地排序:借助了长度分别为 𝑛 和 𝑚 的数组 res 和 counter 。
稳定排序:由于向 res 中填充元素的顺序是“从右向左”的,因此倒序遍历 nums 可以避免改变相等元素之间的相对位置,从而实现稳定排序。实际上,正序遍历 nums 也可以得到正确的排序结果,但结果是非稳定的。
局限性
仅通过统计数量就可以实现高效的排序。然而,使用计数排序的前置条件相对较为严格。
计数排序只适用于非负整数。若想将其用于其他类型的数据,需要确保这些数据可以转换为非负整数,并且在转换过程中不能改变各个元素之间的相对大小关系。例如,对于包含负数的整数数组,可以先给所有数字加上一个常数,将全部数字转化为正数,排序完成后再转换回去。
计数排序适用于数据量大但数据范围较小的情况。比如,在上述示例中 𝑚 不能太大,否则会占用过多空间。而当 𝑛 ≪ 𝑚 时,计数排序使用 𝑂(𝑚) 时间,可能比 𝑂(𝑛 log 𝑛) 的排序算法还要慢。
基数排序
基数排序的核心思想与计数排序一致,也通过统计个数来实现排序。
在此基础上,基数排序利用数字各位之间的递进关系,依次对每一位进行排序,从而得到最终的排序结果。
以学号数据为例,假设数字的最低位是第 1 位,最高位是第 8 位,基数排序的流程如图:

对于一个 𝑑 进制的数字 𝑥 ,要获取其第 𝑘 位 𝑥_𝑘 ,可以使用以下计算公式:
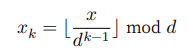
其中 ⌊𝑎⌋ 表示对浮点数 𝑎 向下取整,而 mod 𝑑 表示对 𝑑 取模(取余)。对于学号数据,𝑑 = 10 且 𝑘 ∈ [1, 8]。
/*** File: radix_sort.cpp* Created Time: 2023-03-26* Author: Krahets (krahets@163.com)*/#include "../utils/common.hpp"/* 获取元素 num 的第 k 位,其中 exp = 10^(k-1) */
int digit(int num, int exp) {// 传入 exp 而非 k 可以避免在此重复执行昂贵的次方计算return (num / exp) % 10;
}/* 计数排序(根据 nums 第 k 位排序) */
void countingSortDigit(vector<int> &nums, int exp) {// 十进制的位范围为 0~9 ,因此需要长度为 10 的桶数组vector<int> counter(10, 0);int n = nums.size();// 统计 0~9 各数字的出现次数for (int i = 0; i < n; i++) {int d = digit(nums[i], exp); // 获取 nums[i] 第 k 位,记为 dcounter[d]++; // 统计数字 d 的出现次数}// 求前缀和,将“出现个数”转换为“数组索引”for (int i = 1; i < 10; i++) {counter[i] += counter[i - 1];}// 倒序遍历,根据桶内统计结果,将各元素填入 resvector<int> res(n, 0);for (int i = n - 1; i >= 0; i--) {int d = digit(nums[i], exp);int j = counter[d] - 1; // 获取 d 在数组中的索引 jres[j] = nums[i]; // 将当前元素填入索引 jcounter[d]--; // 将 d 的数量减 1}// 使用结果覆盖原数组 numsfor (int i = 0; i < n; i++)nums[i] = res[i];
}/* 基数排序 */
void radixSort(vector<int> &nums) {// 获取数组的最大元素,用于判断最大位数int m = *max_element(nums.begin(), nums.end());// 按照从低位到高位的顺序遍历for (int exp = 1; exp <= m; exp *= 10)// 对数组元素的第 k 位执行计数排序// k = 1 -> exp = 1// k = 2 -> exp = 10// 即 exp = 10^(k-1)countingSortDigit(nums, exp);
}/* Driver Code */
int main() {// 基数排序vector<int> nums = {10546151, 35663510, 42865989, 34862445, 81883077,88906420, 72429244, 30524779, 82060337, 63832996};radixSort(nums);cout << "基数排序完成后 nums = ";printVector(nums);return 0;
}
为什么从最低位开始排序?
在连续的排序轮次中,后一轮排序会覆盖前一轮排序的结果。举例来说,如果第一轮排序结果 𝑎 < 𝑏 ,而第二轮排序结果 𝑎 > 𝑏 ,那么第二轮的结果将取代第一轮的结果。由于数字的高位优先级高于低位,因此应该先排序低位再排序高位。
算法特性
相较于计数排序,基数排序适用于数值范围较大的情况,但前提是数据必须可以表示为固定位数的格式,且位数不能过大。例如,浮点数不适合使用基数排序,因为其位数 𝑘 过大,可能导致时间复杂度 𝑂(𝑛𝑘) ≫ 𝑂(𝑛^2)。
时间复杂度为 𝑂(𝑛𝑘):设数据量为 𝑛、数据为 𝑑 进制、最大位数为 𝑘 ,则对某一位执行计数排序使用 𝑂(𝑛 + 𝑑) 时间,排序所有 𝑘 位使用 𝑂((𝑛 + 𝑑)𝑘) 时间。通常情况下,𝑑 和 𝑘 都相对较小,时间复杂度趋向 𝑂(𝑛) 。
空间复杂度为 𝑂(𝑛 + 𝑑)、非原地排序:与计数排序相同,基数排序需要借助长度为 𝑛 和 𝑑 的数组 res 和 counter 。
稳定排序:当计数排序稳定时,基数排序也稳定;当计数排序不稳定时,基数排序无法保证得到正确的
排序结果。
小结
学习地址
学习地址:https://github.com/krahets/hello-algo
重新复习数据结构,所有的内容都来自这里。
相关文章:

数据结构和算法:十大排序
排序算法 排序算法用于对一组数据按照特定顺序进行排列。排序算法有着广泛的应用,因为有序数据通常能够被更高效地查找、分析和处理。 排序算法中的数据类型可以是整数、浮点数、字符或字符串等。排序的判断规则可根据需求设定,如数字大小、字符 ASCII…...
LLaMA-Factory微调(sft)ChatGLM3-6B保姆教程
LLaMA-Factory微调(sft)ChatGLM3-6B保姆教程 准备 1、下载 下载LLaMA-Factory下载ChatGLM3-6B下载ChatGLM3windows下载CUDA ToolKit 12.1 (本人是在windows进行训练的,显卡GTX 1660 Ti) CUDA安装完毕后,…...

Web安全-浏览器安全策略及跨站脚本攻击与请求伪造漏洞原理
Web安全-浏览器安全策略及跨站脚本攻击与请求伪造漏洞原理 Web服务组件分层概念 静态层 :web前端框架:Bootstrap,jQuery,HTML5框架等,主要存在跨站脚本攻击脚本层:web应用,web开发框架,web服务…...
)
蓝桥杯B组C++省赛——飞机降落(DFS)
题目连接:https://www.lanqiao.cn/problems/3511/learning/ 思路:由于数据范围很小,所有选择用DFS枚举所有飞机的所有的降落顺序,看哪个顺序可以让所有飞机顺利降落,有的话就算成功方案,输出了“YES”。 …...

Java 中的 Map集合
文章目录 添加和修改元素获取元素检查元素删除元素获取所有键 / 值 / 键值对大小 在 Java 中,Map 接口是 Java 集合框架的一部分,它存储键值对(key-value pairs)。Map 接口有许多常用的方法,用于添加、删除、获取元素&…...
基于springboot大学生兼职平台管理系统(完整源码+数据库)
一、项目简介 本项目是一套基于springboot大学生兼职平台管理系统 包含:项目源码、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都经过严格调试,eclipse或者idea 确保可以运行! 该系统功能完善、界面美观、操作简单、功…...
C#学生信息管理系统
一、引言 学生信息管理系统是现代学校管理的重要组成部分,它能够有效地管理学生的基本信息、课程信息、成绩信息等,提高学校管理的效率和质量。本文将介绍如何使用SQL Server数据库和C#语言在.NET平台上开发一个学生信息管理系统的课程设计项目。 二、项…...

双机 Cartogtapher 建图文件配置
双机cartogtapher建图 最近在做硕士毕设的最后一个实验,其中涉及到多机建图,经过调研最终采用cartographer建图算法,其中配置多机建图的文件有些麻烦,特此博客以记录 非常感谢我的同门 ”叶少“ 山上的稻草人-CSDN博客的帮助&am…...
VMware提示 该虚拟机似乎正在使用中,如何解决?
VMware提示 该虚拟机似乎正在使用中,如何解决? 问题描述解决方法1.找到安装VMware的文件目录2.在VMware目录下.lck后缀的文件夹删除或重命名3.运行VMware 问题描述 该虚拟机似乎正在使用中。 如果该虚拟机未在使用,请按“获取所有权(T)”按钮获取它的所…...
阿里云短信服务业务
一、了解阿里云用户权限操作 1.注册账号、实名认证; 2.使用AccessKey 步骤一 点击头像,权限安全的AccessKey 步骤二 设置子用户AccessKey 步骤三 添加用户组和用户 步骤四 添加用户组记得绑定短信服务权限 步骤五 添加用户记得勾选openApi访问 添加…...

ElasticSearch的DSL查询
ElasticSearch的DSL查询 准备工作 创建测试方法,初始化测试结构。 import org.apache.http.HttpHost; import org.apache.lucene.search.TotalHits; import org.elasticsearch.action.search.SearchRequest; import org.elasticsearch.action.search.SearchRespo…...

每天定时杀spark进程
##编写shell脚本 #!/bin/bash arr(“zhangsan” “lisi” “wangwu”) for i in “${arr[]}” do processps -ef|grep ${i}| grep -v "grep"| awk {print $2} kill -9 ${process} done ##每日定时杀手动启动的进程 0 19 * * * cd /kill_process && sh kil…...

win10 安装kubectl,配置config连接k8s集群
安装kubectl 按照官方文档安装:https://kubernetes.io/docs/tasks/tools/install-kubectl-windows/ curl安装 (1)下载curl安装压缩包: curl for Windows (2)配置环境变量: 用户变量: Path变…...
Calico IPIP和BGP TOR的数据包走向
IPIP Mesh全网互联 文字描述 APOD eth0 10.7.75.132 -----> APOD 网关 -----> A宿主机 cali76174826315网卡 -----> Atunl0 10.7.75.128 封装 ----> Aeth0 10.120.181.20 -----> 通过网关 10.120.181.254 -----> 下一跳 BNODE eth0 10.120.179.8 解封装 --…...

静态成员主要用于提供与类本身相关的功能或数据,有什么应用场景
静态成员(包括静态方法和静态属性)在JavaScript中常用于多种应用场景,它们为类提供了与类本身直接相关而不是与实例相关的功能或数据。以下是一些常见的应用场景: 工厂方法 静态方法可以作为工厂方法,用于创建类的实…...

在线考试|基于Springboot的在线考试管理系统设计与实现(源码+数据库+文档)
在线考试管理系统目录 目录 基于Springboot的在线考试管理系统设计与实现 一、前言 二、系统设计 三、系统功能设计 1、前台: 2、后台 管理员功能 四、数据库设计 五、核心代码 六、论文参考 七、最新计算机毕设选题推荐 八、源码获取: 博主…...

C语言-----数据在内存中的存储(1)
1.整数在内存中的存储 我们之前就了解过整数的二进制写法分别有3种,分别为原码,反码,补码。整型在内存中存储的是补码。 原码,反码,补码都有自己的符号位和数值位,符号位为1时,则表示负数&…...
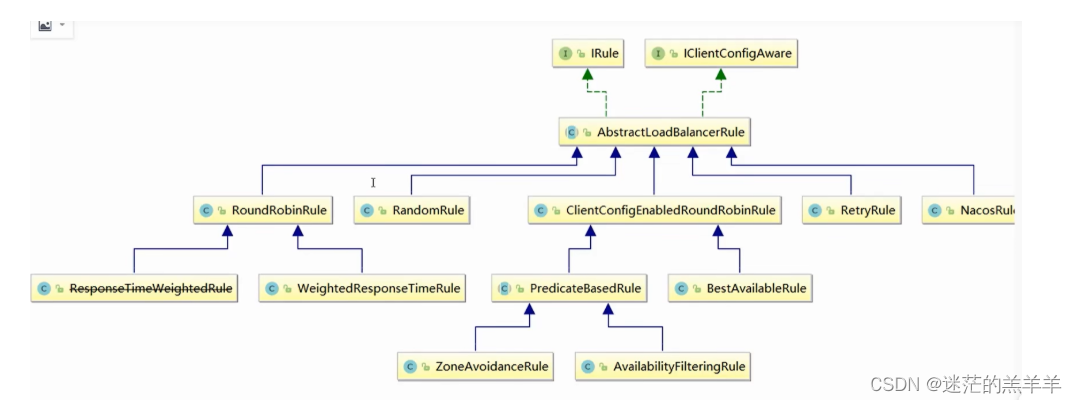
Ribbon有哪些负载均衡策略
负载均衡类都实现了IRule接口。 RandomRule:随机的选用一个实例 RoundRobinRule:轮询的使用实例 RetryRule:在轮询的基础上加了一个错误重试机制,在deadline时间内会不断的重试 WeightResponeTimeRule:根据权重去做…...

websocket多级nginx代理
在使用多层Nginx代理时,WebSocket的连接可能会遇到一些问题,因为WebSocket连接是持久化的,它需要Upgrade头部来确认升级到WebSocket协议。在多层代理的情况下,每层代理可能会修改或丢失这个Upgrade头部信息。 为了确保WebSocket能…...
【python从入门到精通】-- 第四战:语句汇总
🌈 个人主页:白子寰 🔥 分类专栏:python从入门到精通,魔法指针,进阶C,C语言,C语言题集,C语言实现游戏👈 希望得到您的订阅和支持~ 💡 坚持创作博文…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
