复位和时钟控制(RCC)
目录
复位
系统复位
电源复位
备份区复位
时钟控制
什么是时钟?
时钟来源
二级时钟源:
如何使用CubeMX配置时钟
复位
系统复位
- 1. NRST引脚上的低电平(外部复位)
- 2. 窗口看门狗计数终止(WWDG复位)
- 3. 独立看门狗计数终止(IWDG复位)
- 4. 软件复位(SW复位)
- 5. 低功耗管理复位
电源复位
- 1. 上电/掉电复位(POR/PDR复位)
- 2. 从待机模式中返回
备份区复位
- 1. 软件复位,备份区域复位可由设置备份域控制寄存器 (RCC_BDCR)(见6.3.9节)中的 BDRST位产生。
- 2. 在VDD和VBAT两者掉电的前提下,VDD或VBAT上电将引发备份区域复位。
时钟控制
什么是时钟?
时钟来源
三种不同的时钟源可被用来驱动系统时钟(SYSCLK)
- HSI振荡器时钟(高速内部时钟)
- HSE振荡器时钟(高速外部时钟)
- PLL时钟(锁相环倍频时钟)
二级时钟源:
- 40kHz低速内部RC(LSIRC)振荡器
- 32.768kHz低速外部晶体(LSE晶体)
如何使用CubeMX配置时钟
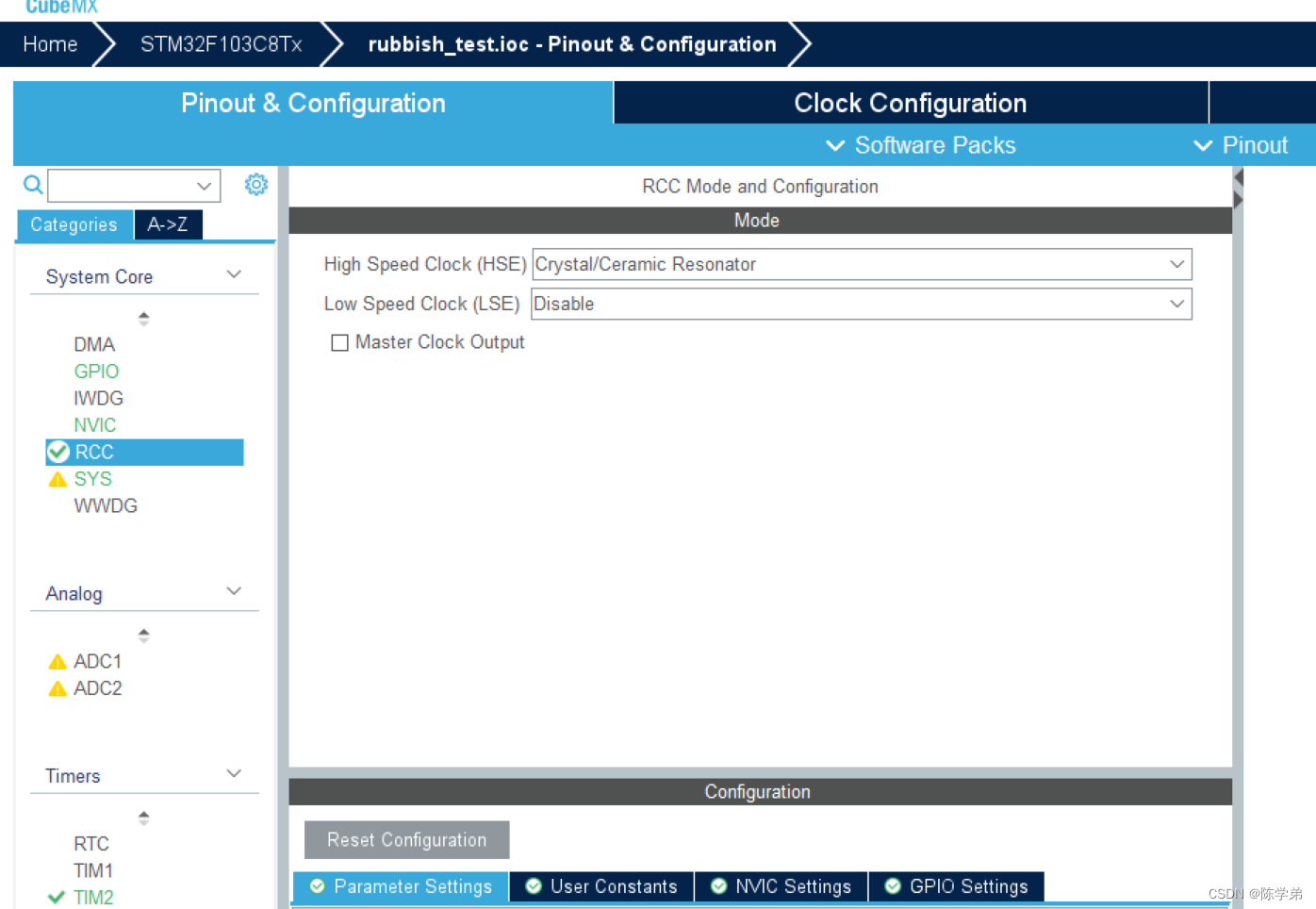
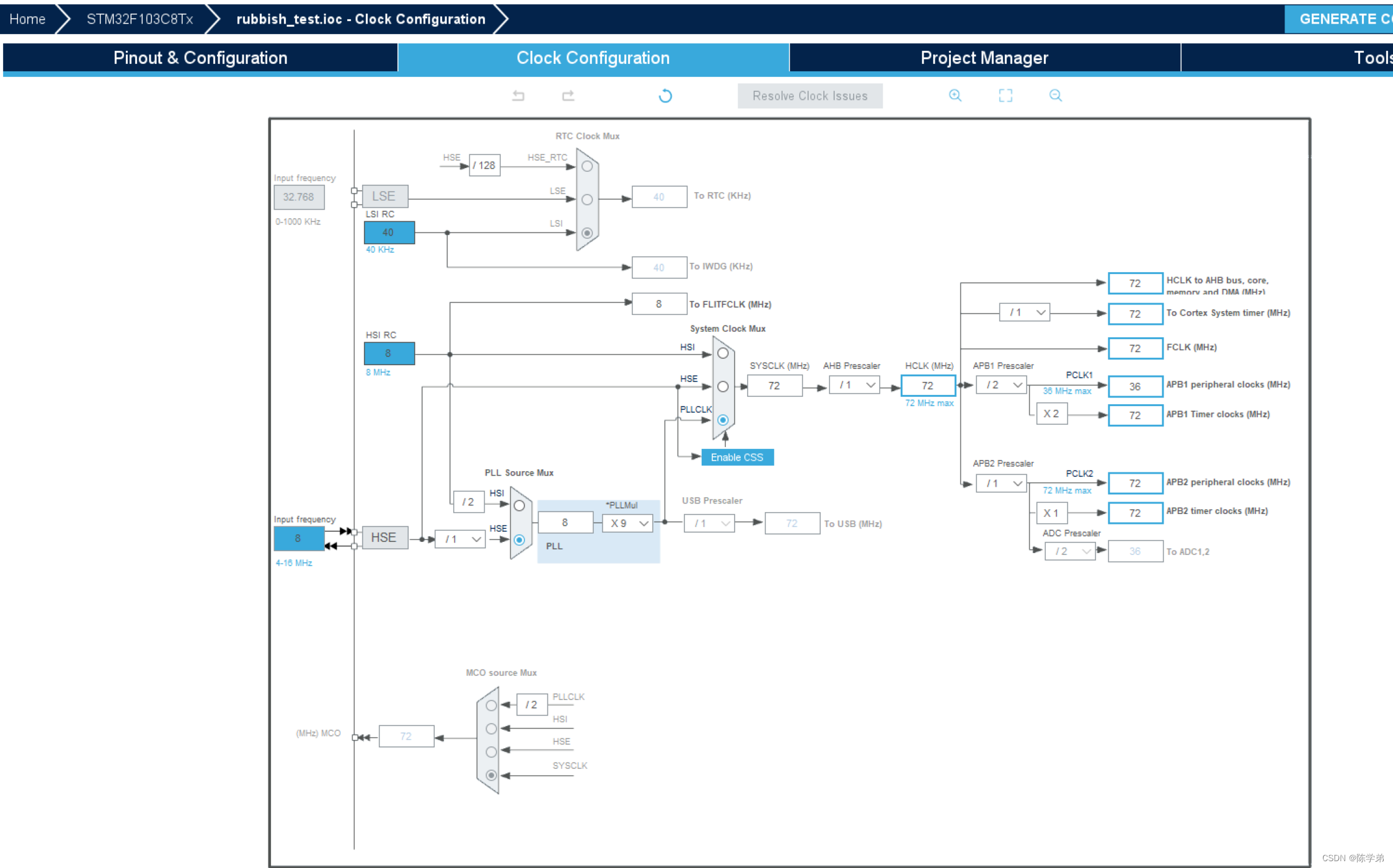
相关文章:

复位和时钟控制(RCC)
目录 复位 系统复位 电源复位 备份区复位 时钟控制 什么是时钟? 时钟来源 二级时钟源: 如何使用CubeMX配置时钟 复位 系统复位 当发生以下任一事件时,产生一个系统复位:1. NRST引脚上的低电平(外部复位) 2. 窗口看门狗计数终止(WWD…...

OpenWrt 专栏介绍00
文章目录OpenWrt 专栏介绍00专栏章节介绍关于联系方式OpenWrt 专栏介绍00 专栏章节介绍 本专栏主要从开发者角度,一步步深入理解OpenWrt开发流程,本专栏包含以下章节,内如如下: 01.OperWrt 环境搭建02.OperWrt 包管理系统03.Op…...

udk开发-稀里糊涂
一、EDK2简介 1.EDK2工作流 二、EDK2 Packages 1.Packages介绍 EDK2 Packages是一个容器,其中包含一组模块及模块的相关定义。每个Package是一个EDK2单元。 整个Project的源代码可以被分割成不同的Pkg。这样的设计不仅可以降低耦合性,还有利于分…...

Java之内部类
目录 一.内部类 1.什么是内部类 2.内部类存在的原因 3. 内部类的分类 4.内部类的作用 二.成员内部类 1.基本概念 2.成员内部类的注意点 1.成员内部类可以用private方法进行修饰 2.成员内部类可以直接访问外部类的私有属性 3.外部类可以通过对象访问内部类的私有属性 …...
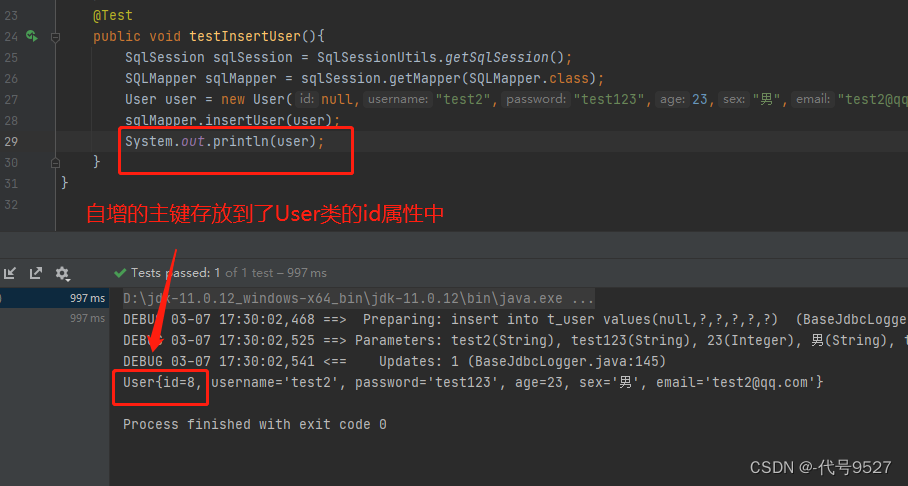
【MyBatis】篇二.MyBatis查询与特殊SQL
文章目录1、MyBatis获取参数值case1-单个字面量类型的参数case2-多个字面量类型的参数case3-map集合类型的参数case4-实体类类型的参数case5-使用Param注解命名参数总结2、MyBatis的各种查询功能case1-查询结果是一个实体类对象case2-查询结果是一个List集合case3-查询单个数据…...

CE认证机构和CE证书的分类
目前,CE认证已普遍被应用在很多行业的商品中,也是企业商品进入欧洲市场的必备安全合格认证。在船舶海工行业中,也同样普遍应用,很多时候,对于规范中没有明确认证要求的设备或材料,而船舶将来还会去欧洲水域…...

Lesson 8.2 CART 分类树的建模流程与 sklearn 评估器参数详解
文章目录一、CART 决策树的分类流程1. CART 树的基本生长过程1.1 规则评估指标选取与设置1.2 决策树备选规则创建方法1.3 挑选最佳分类规则划分数据集1.4 决策树的生长过程2. CART 树的剪枝二、CART 分类树的 Scikit-Learn 快速实现方法与评估器参数详解1. CART 分类树的 sklea…...

【Unity】程序集Assembly模块化开发
笔者按:使用Unity版本为2021.3LTS,与其他版本或有异同。请仅做参考 一、简述。 本文是笔者在学习使用Unity引擎的过程中,产学研的一个笔记。由笔者根据官方文档Unity User Manual 2021.3 (LTS)/脚本/Unity 架构/脚本编译/程序集定义相关部分结…...

马尔可夫决策过程
1. 马尔可夫决策过程 马尔可夫决策过程不过是引入"决策"的马氏过程. Pij(a)P{Xn1j∣X0,a0,X1,a1,...,Xni,an1}P{Xnn1j∣Xni,ana}\begin{split} P_{ij}(a) & P\{X_{n1} j|X_0, a_0, X_1, a_1, ..., X_n i, a_n 1\} \\ &P\{X_n{n1} j|X_n i, a_n a\} \e…...
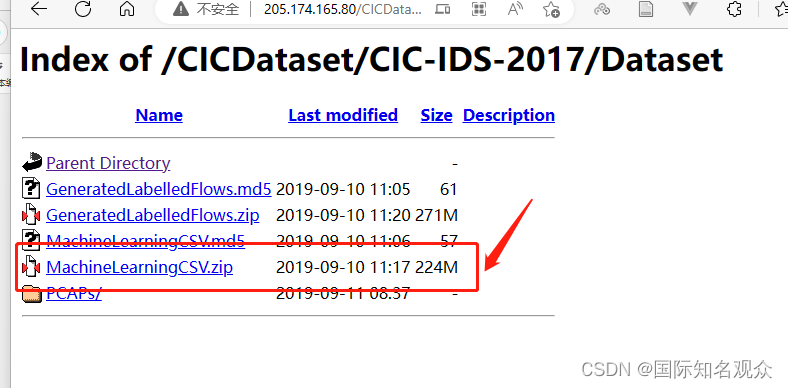
win11下载配置CIC Flowmeter环境并提取流量特征
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、下载CIC Flowmeter二、安装java、maven、gradle和IDEA1.java 1.82.maven3.gradle4.IDEA三、CICFlowMeter-master使用四、流量特征1.含义2.获取前言 配了一整…...
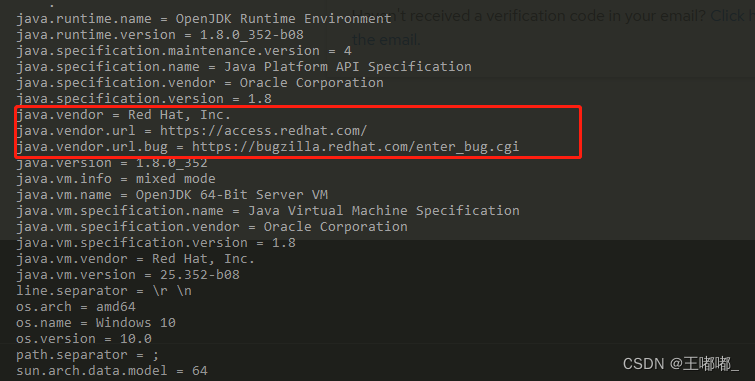
JDK如何判断自己是什么公司的
0x00 前言 因为一些事情,遇到了这样一个问题,JDK如何判断自己是什么公司编译的。因为不同的公司编译出来,涉及到是否商用收费的问题。 平时自己使用的时候,是不会考虑到JDK的编译公司是哪一个,都是直接拿起来用&#…...
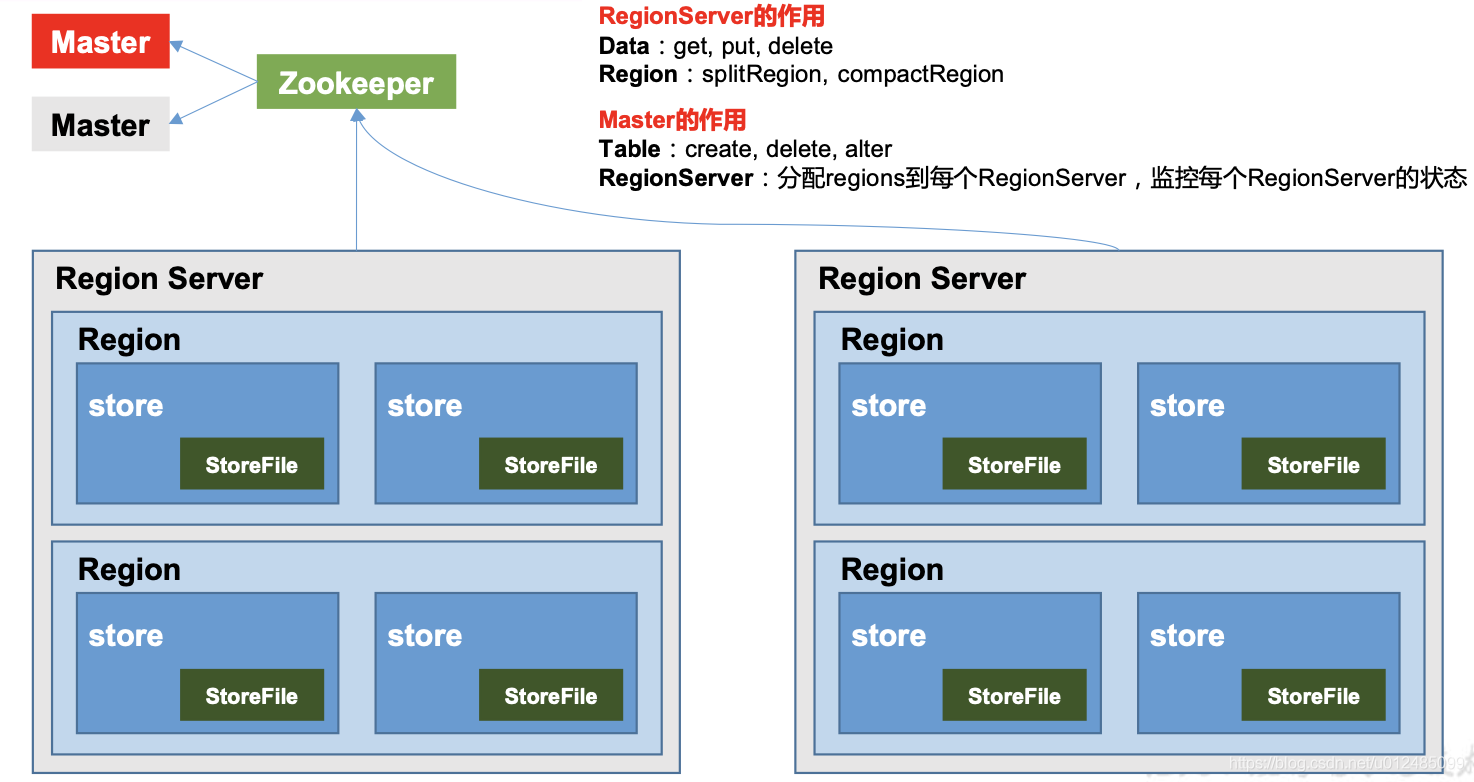
大数据技术之HBase(二)HBase原理简介
一、HBase定义1.1 HBase定义HBase 是一种分布式、可扩展、支持海量数据存储的 NoSQL 数据库非结构化数据存储的数据库,基于列的模式存储。利用Hadoop HDFS作为其文件存储系统,写入性能很强,读取性能较差。利用Hadoop MapReduce来处理HBase中的…...
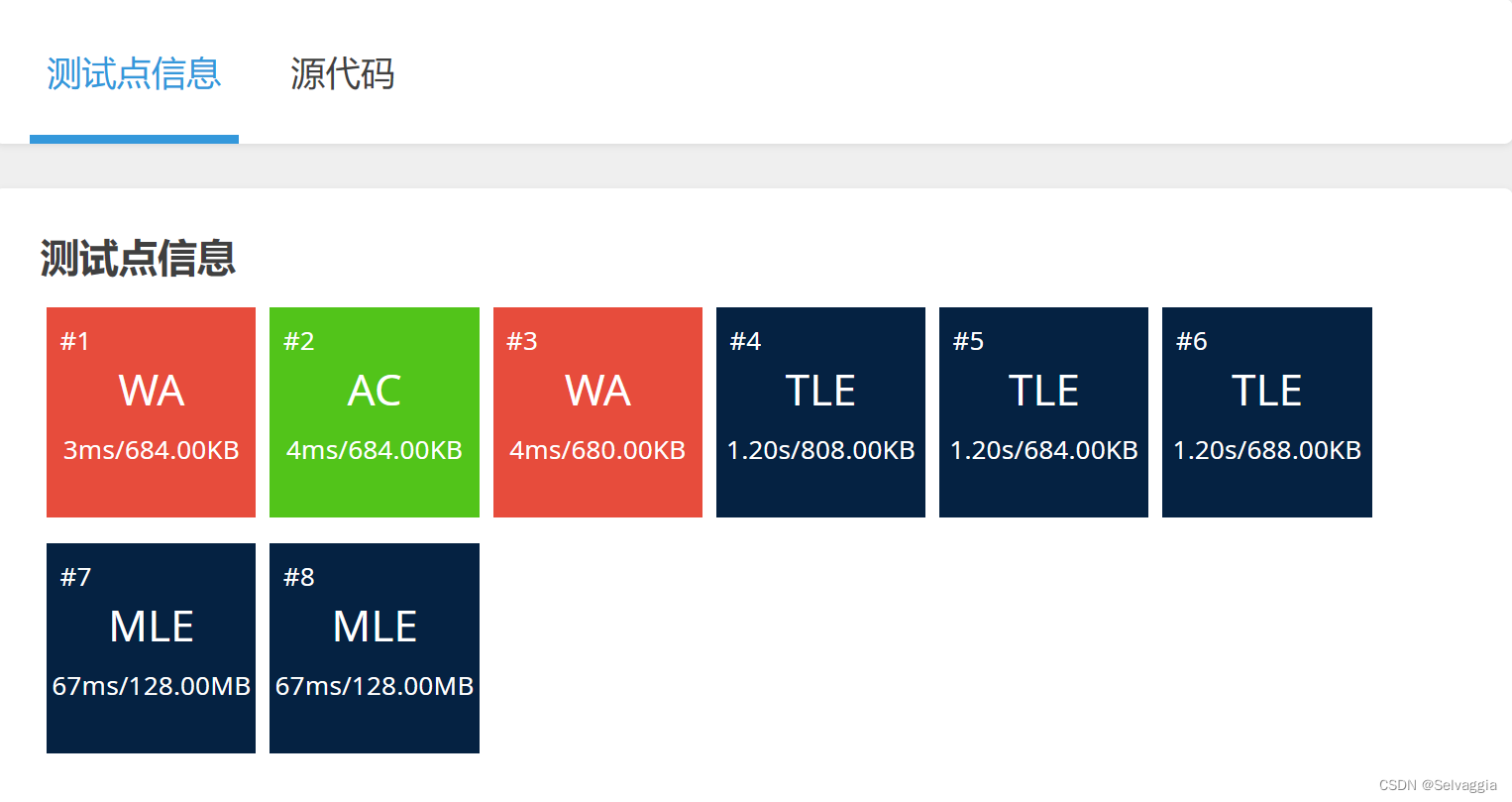
垒骰子(爆搜/DP)
动态规划方格取数垒骰子方格取数 题目描述 设有 NNN \times NNN 的方格图 (N≤9)(N \le 9)(N≤9),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字 000。如下图所示(见样例): A0 0 0 0 0 0 0 00 0 13 0 …...

Telink之标准SDK的介绍_1
前提:常见的项目架构:应用层----》驱动层----》硬件层 1、软件组织架构 顶层⽂件夹( 8 个): algorithm,application,boot,common,drivers,proj_lib,stack,v…...

JNI内两种方式从C/C++中传递一维、二维、三维数组数据至Java层详细梳理
目录 0 前言 1 准备工作介绍 2 一维数组 2.1 return形式 2.2 参数形式 3 二维数组 3.1 return形式 3.2 参数形式 4 三维数组 4.1 return形式 4.2 参数形式 5 测试代码 6 结果说明 0 前言 就如之前我写过的一篇文章【JNI内形参从C代码中获取返回值并返回到Java层使…...
)
快递计费系统--课后程序(Python程序开发案例教程-黑马程序员编著-第3章-课后作业)
实例5:快递计费系统 快递行业高速发展,我们邮寄物品变得方便快捷。某快递点提供华东地区、华南地区、华北地区的寄件服务,其中华东地区编号为01、华南地区编号为02、华北地区编号为03,该快递点寄件价目表具体如表1所示。 表1 寄…...

JS - 自定义一周的开始和结束,计算日期所在月的周数、所在月第几周、所在周的日期范围
自定义一周的开始和结束,计算日期所在月的周数、所在月第几周、所在周的日期范围一. 方法使用二. 实现案例一. 方法使用 根据月开始日期星期几、月结束日期星期几,计算始周、末周占月的天数(每周周期段:上周六 —— 本周五&#x…...

Linux :理解编译的四个阶段
目录一、了解编译二、认识编译的四个阶段(一)预处理(二)编译(三)汇编(四)链接1.静态链接2.动态链接三、分步编译(一)创建.c文件(二)预…...

197.Spark(四):Spark 案例实操,MVC方式代码编程
一、Spark 案例实操 1.数据准备 电商网站的用户行为数据,主要包含用户的 4 种行为:搜索,点击,下单,支付 样例类: 2. Top10 热门品类 先按照点击数排名,靠前的就排名高;如果点击数相同,再比较下单数;下单数再相同,就比较支付数。 我们有多种写法,越往后性能越…...
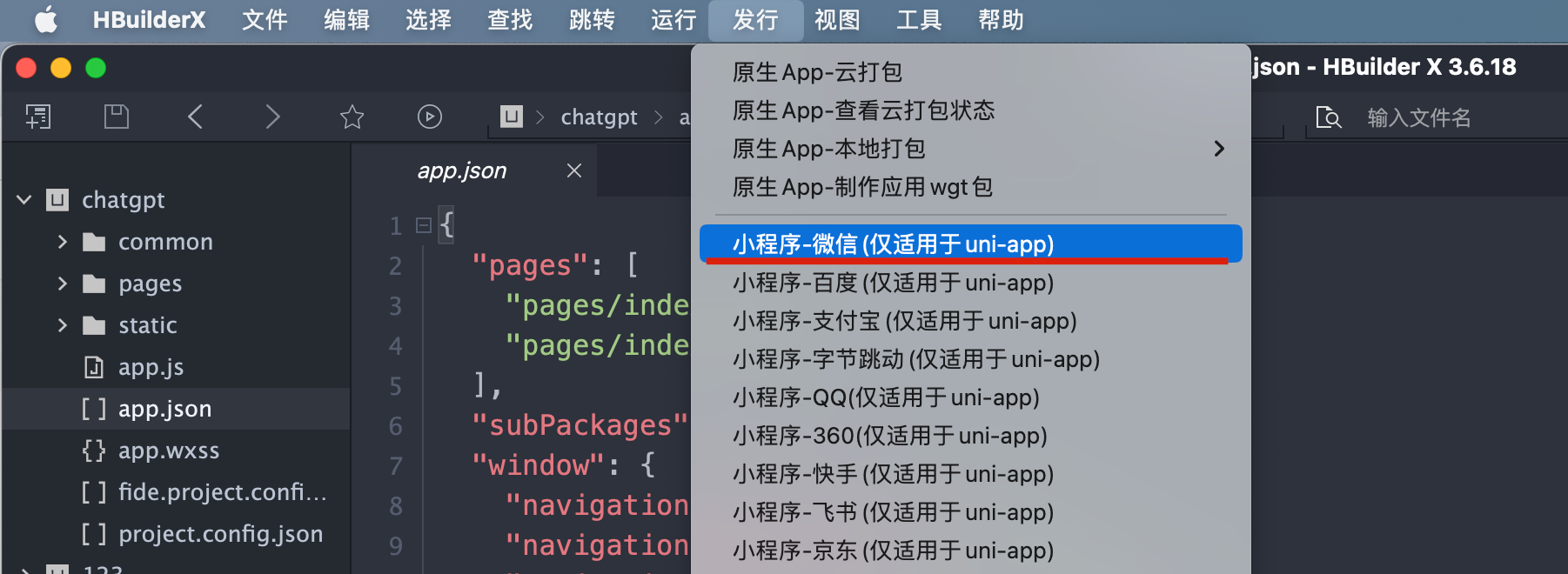
Vue 项目如何迁移小程序
最近我们看到有开发者在社群里提出新的疑惑「我手头已经有一个成熟的 HTML5 项目了,这种项目可以转为小程序在 FinClip 环境中运行吗?」。 经过工作人员的沟通了解,开发者其实是想将已有的 Vue 项目转为小程序,在集成了 FinClip …...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
