当前位置： 首页 > news >正文

子集(迭代)(leetcode 78)

news 2025/10/28 5:25:37

核心逻辑：

根据子数组包含的元素个数迭代：

现有子集的基础上通过添加这个新元素来翻倍子集的数量        f(n)=2×f(n−1)

    vector<vector<int>> subsets(vector<int>& nums) {vector<vector<int>> ans;int i,j,k;ans.push_back({});for(i = 0; i < nums.size(); i++){k = ans.size();for(j = 0; j < k; j++){vector<int> e = ans[j];e.push_back(nums[i]);ans.push_back(e);}}return ans;}

相关文章：

子集(迭代)(leetcode 78)

核心逻辑&#xff1a; 根据子数组包含的元素个数迭代&#xff1a; 现有子集的基础上通过添加这个新元素来翻倍子集的数量 f(n)2f(n−1) vector<vector<int>> subsets(vector<int>& nums) {vector<vector<int>> ans;int i,j,k;ans.p…...

编程日记 2024/4/7 9:19:57

汽车疲劳测试试验平台技术要求（北重厂家）

汽车疲劳测试试验平台技术要求通常包括以下几个方面&#xff1a; 车辆加载能力&#xff1a;测试平台需要具备足够的承载能力&#xff0c;能够同时测试多种车型和不同重量的车辆。 动力系统&#xff1a;测试平台需要具备稳定可靠的动力系统&#xff0c;能够提供足够的力和速度来…...

编程日记 2024/4/7 9:11:49

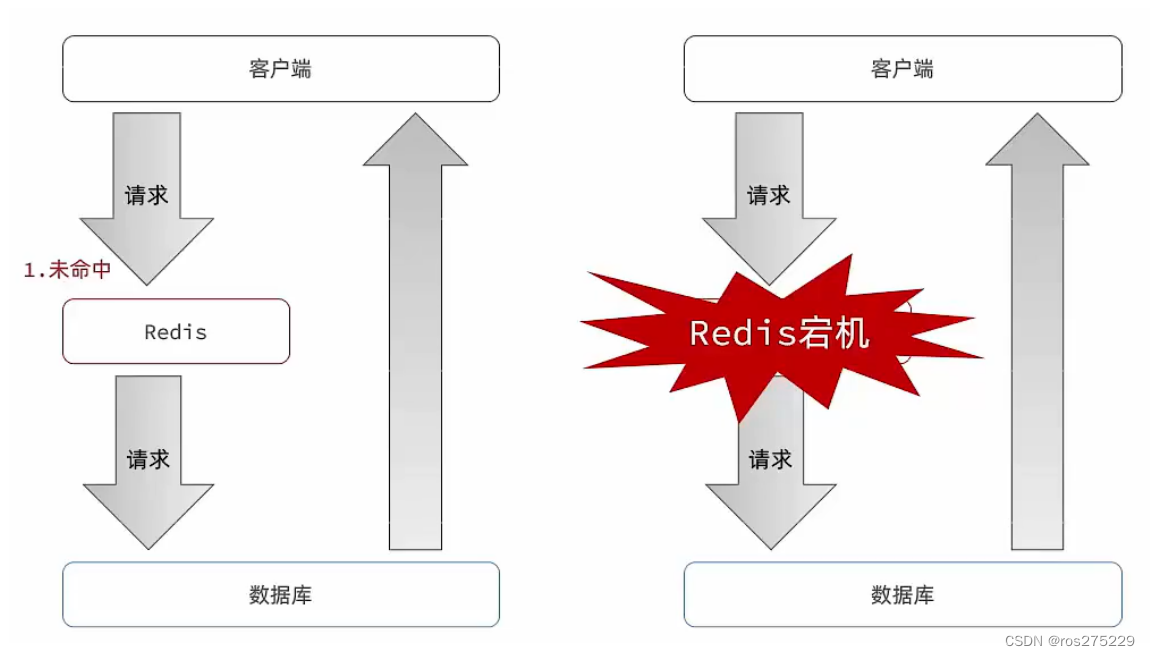
Redis -- 缓存雪崩问题

缓存雪崩是指在同一时段大量的缓存key同时失效或者Redis服务宕机&#xff0c;导致大量请求到达数据库&#xff0c;带来巨大压力。 可能原因 : 同一时间大量的key到期 ; 解决方案&#xff1a; 给不同的Key的TTL添加随机值 利用Redis集群提高服务的可用性 给缓存业务添加降…...

编程日记 2024/4/7 9:10:47

【ARM 嵌入式 C 文件操作系列 20 -- 文件删除函数 remove 详细介绍】

请阅读【嵌入式开发学习必备专栏 】 文章目录 文件删除函数 remove 文件删除函数 remove 在 C 语言中&#xff0c; 可以使用 remove 函数来删除一个文件&#xff0c;但在删除之前 可能想确认该文件是否存在。 可以使用 stat 函数来检查文件是否存在。 以下是如何实现这个功能…...

编程日记 2024/4/7 9:09:46

LeetCode刷题之31.下一个排列

文章目录 1. 题目2.分析3.解答3.1 先排序&#xff0c;后交换3.2 先交换&#xff0c;后排序 1. 题目 整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。 例如&#xff0c;arr [1,2,3] &#xff0c;以下这些都可以视作 arr 的排列&#xff1a;[1,2,3]、[1,3,2]、[3…...

编程日记 2024/4/7 9:06:43

【RISC-V 指令集】RISC-V 向量V扩展指令集介绍(九)- 向量定点算术指令

1. 引言 以下是《riscv-v-spec-1.0.pdf》文档的关键内容&#xff1a; 这是一份关于向量扩展的详细技术文档&#xff0c;内容覆盖了向量指令集的多个关键方面&#xff0c;如向量寄存器状态映射、向量指令格式、向量加载和存储操作、向量内存对齐约束、向量内存一致性模型、向量…...

编程日记 2024/4/7 9:05:41

【Java网络编程】IP网络协议与TCP、UDP网络传输层协议

1.1、IP协议 当应用层的数据被封装后&#xff0c;想要将数据在网络上传输&#xff0c;数据究竟要被发往何处&#xff0c;又该如何精准的在网络上定位目标机器&#xff0c;此时起到关键作用的就是“IP协议”。IP协议的作用在于把各种数据包准确无误的传递给目标方&#xff0c;其…...

编程日记 2024/4/7 9:04:40

C# 分布式自增ID算法snowflake（雪花算法）

文章目录 1. 概述2. 结构3. 代码3.1 IdWorker.cs3.2 IdWorkerTest.cs (测试) 1. 概述 分布式系统中&#xff0c;有一些需要使用全局唯一ID的场景&#xff0c;这种时候为了防止ID冲突可以使用36位的UUID&#xff0c;但是UUID有一些缺点&#xff0c;首先他相对比较长&#xff0c…...

编程日记 2024/4/7 9:03:38

commonJS和esModule的应用

commonJS commonJS规范的核心变量是&#xff1a;exports&#xff0c;module.exports&#xff0c;require exports 和 module.exports可以负责模块的导出require 负责模块的导入 module.exports 导出方案&#xff1a; const name yx const age 18// 1 导出方案 module.exp…...

编程日记 2024/4/7 9:02:37

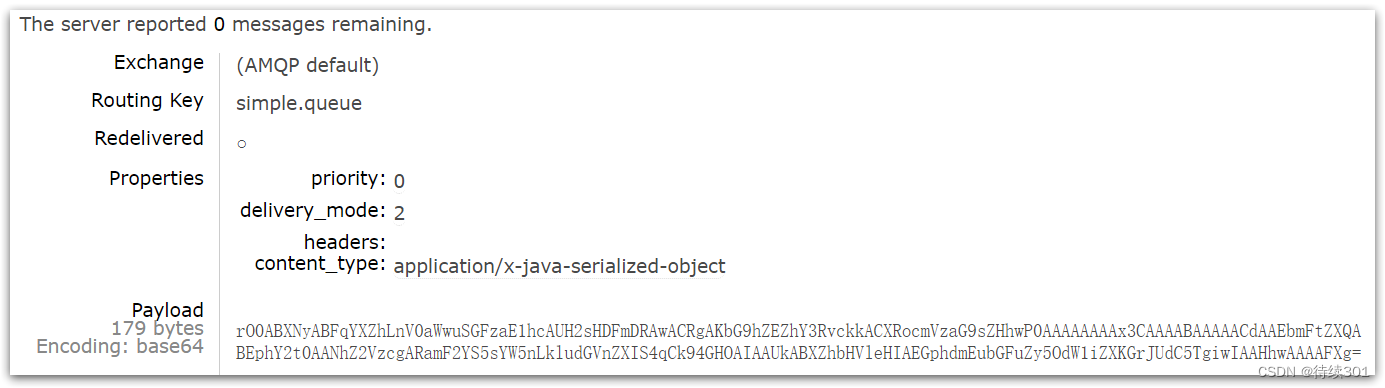
（十一）RabbitMQ及SpringAMQP

1.初识MQ 1.1.同步和异步通讯 微服务间通讯有同步和异步两种方式&#xff1a; 同步通讯&#xff1a;就像打电话&#xff0c;需要实时响应。 异步通讯&#xff1a;就像发邮件&#xff0c;不需要马上回复。 两种方式各有优劣&#xff0c;打电话可以立即得到响应&#xff0c;…...

编程日记 2024/4/7 9:00:35

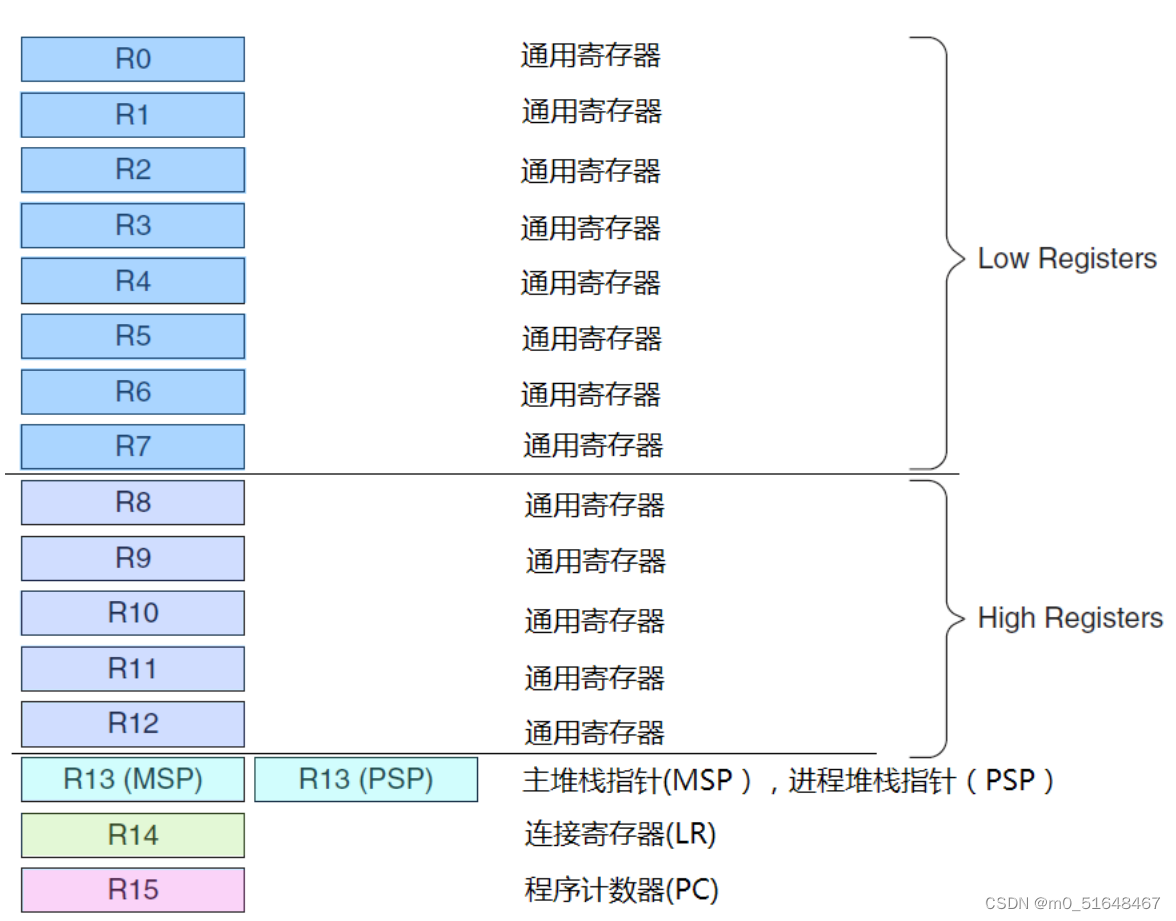
STM32 M3内核寄存器概念

内容主要来自<<M3内核权威指南>> 汇编程序中的最低有效位&#xff08;Least Significant Bit&#xff09;。LSB是二进制数中最右边的位&#xff0c;它代表了数值中的最小单位。在汇编程序中&#xff0c;LSB通常用于表示数据的最小精度或者作为标志位。 ---------…...

编程日记 2024/4/7 8:58:32

SQL语句的编写

##创建用户-建表建库 #创建一个用户名为 feng&#xff0c;允许从任何主机 % 连接&#xff0c;并使用密码 sc123456 进行身份验证的用户。 rootTENNIS 16:33 scmysql>create user feng% identified by sc123456; Query OK, 0 rows affected (0.04 sec) #创建一个名为fen…...

编程日记 2024/4/7 8:55:29

Lecture 1~3 About Filter

文章目录 空间域上的滤波器- 线性滤波器盒状滤波器Box Filter锐化Sharpening相关运算 vs. 卷积运算 Correlation vs. Convolution - 非线性滤波器高斯滤波器Gaussian filter - 实际问题- 纹理texture 频域上的滤波器 滤波的应用- 模板匹配- 图像金字塔 空间域上的滤波器 图像…...

编程日记 2024/4/7 8:49:24

配置vscode链接linux

1.安装 remote SSH 2.按F1 ssh ljh服务器公网ip 3. 选择保存远端host到本地 某位置 等待片刻后 4. 切换到远程资源管理器中 应该可以看到一台电脑&#xff0c;右键在当前窗口链接&#xff0c;输入你的服务器用户密码后电脑变绿说明远程连接成功 5.一定要登陆上云服务器后再…...

编程日记 2024/4/7 8:46:21

论文阅读——MVDiffusion

MVDiffusion: Enabling Holistic Multi-view Image Generation with Correspondence-Aware Diffusion 文生图模型 用于根据给定像素到像素对应关系的文本提示生成一致的多视图图像。 MVDiffusion 会在给定任意每个视图文本的情况下合成高分辨率真实感全景图像&#xff0c;或将…...

编程日记 2024/4/7 8:45:20

Linux中的网络命令深度解析与CentOS实践

Linux中的网络命令深度解析与CentOS实践 在Linux系统中，网络命令是管理和诊断网络问题的关键工具。无论是网络管理员还是系统开发者，熟练掌握这些命令都是必不可少的。本文将深入探讨Linux中常用的网络命令，并以CentOS为例，展示这些命令的具体应用。 一、ping命令 ping命…...

编程日记 2024/4/7 8:44:19

nginx配置实例（反向代理）

目录 一、目标-反向代理实现效果 二、安装tomcat 三、配置nginx服务 四、配置反向代理 一、目标-反向代理实现效果 访问过程分析&#xff1a; 二、安装tomcat 1、安装jdk环境 新建/export/server目录 解压jdk 查看是否解压成功 配置jdk软连接 进入jdk的bin目录中&#x…...

编程日记 2024/4/7 8:43:18

Flutter 解决NestedScrollView与TabBar双列表滚动位置同步问题

文章目录 前言一、需要实现的效果如下二、flutter实现代码如下&#xff1a;总结 前言 最近写flutter项目&#xff0c;遇到NestedScrollView与TabBar双列表滚动位置同步问题&#xff0c;下面是解决方案&#xff0c;希望帮助到大家。 一、需要实现的效果如下 1、UI图&#xff1…...

编程日记 2024/4/7 8:42:17

云计算存在的安全隐患

目录 一、概述 二、ENISA云安全漏洞分析 三、云计算相关系统漏洞 3.1 概述 3.2 漏洞分析 3.2.1 Hypervisor漏洞 3.2.1.1 CVE-2018-16882 3.2.1.2 CVE-2017-17563 3.2.1.3 CVE-2010-1225 3.2.2 虚拟机漏洞 3.2.2.1 CVE-2019-14835 3.2.2.2 CVE-2019-5514 3.2.2.3 CV…...

编程日记 2024/4/7 8:38:13

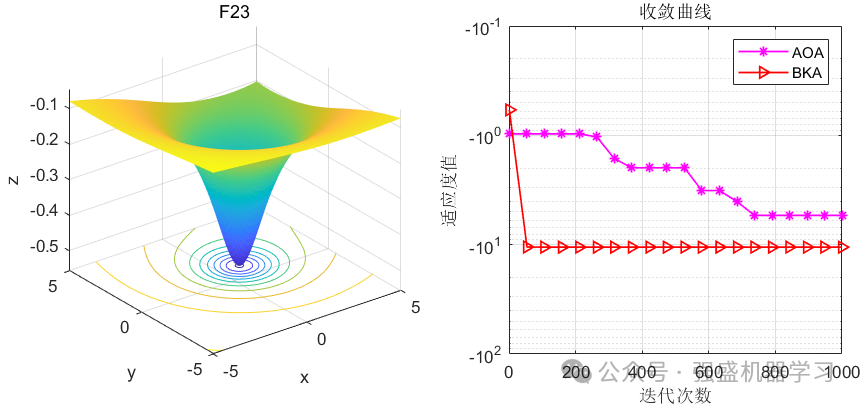
黑翅鸢优化算法(BKA)-2024年SCI一区新算法-公式原理详解与性能测评 Matlab代码免费获取

声明&#xff1a;文章是从本人公众号中复制而来&#xff0c;因此&#xff0c;想最新最快了解各类智能优化算法及其改进的朋友&#xff0c;可关注我的公众号&#xff1a;强盛机器学习&#xff0c;不定期会有很多免费代码分享~ 目录 原理简介 一、种群初始化 二、攻击行为 三…...

编程日记 2024/4/7 8:36:11

调用支付宝接口响应40004 SYSTEM_ERROR问题排查

在对接支付宝API的时候&#xff0c;遇到了一些问题&#xff0c;记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

编程新知 2025/10/17 20:43:55

页面渲染流程与性能优化

页面渲染流程与性能优化详解&#xff08;完整版&#xff09; 一、现代浏览器渲染流程&#xff08;详细说明&#xff09; 1. 构建DOM树 浏览器接收到HTML文档后&#xff0c;会逐步解析并构建DOM&#xff08;Document Object Model&#xff09;树。具体过程如下&#xff1a; (…...

编程新知 2025/10/21 14:18:33

python爬虫：Newspaper3k 的详细使用（好用的新闻网站文章抓取和解析的Python库）

更多内容请见： 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

编程新知 2025/10/25 7:51:48

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法（ISWC2024）

笔记整理&#xff1a;刘治强&#xff0c;浙江大学硕士生&#xff0c;研究方向为知识图谱表示学习&#xff0c;大语言模型 论文链接&#xff1a;http://arxiv.org/abs/2407.16127 发表会议&#xff1a;ISWC 2024 1. 动机 传统的知识图谱补全&#xff08;KGC&#xff09;模型通过…...

编程新知 2025/10/26 4:58:39

【git】把本地更改提交远程新分支feature_g

创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

编程新知 2025/8/15 18:53:03

零基础设计模式——行为型模式 - 责任链模式

第四部分&#xff1a;行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习&#xff01;行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想&#xff1a;使多个对象都有机会处…...

编程新知 2025/10/24 15:27:29

安卓基础（aar）

重新设置java21的环境&#xff0c;临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的&#xff1a; MyApp/ ├── app/ …...

编程新知 2025/10/2 5:21:30

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf

FTP 客服管理系统 实现kefu123登录&#xff0c;不允许匿名访问&#xff0c;kefu只能访问/data/kefu目录&#xff0c;不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

编程新知 2025/10/26 14:58:46

深入浅出深度学习基础：从感知机到全连接神经网络的核心原理与应用

文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么&#xff1f;1.1.2 感知机的工作原理 1.2 感知机的简单应用&#xff1a;基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

编程新知 2025/10/28 4:59:27

jmeter聚合报告中参数详解

sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample&#xff08;样本数&#xff09; 表示测试中发送的请求数量&#xff0c;即测试执行了多少次请求。 单位&#xff0c;以个或者次数表示。 示例&#xff1a;…...

编程新知 2025/9/22 12:41:30