回归预测 | Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的多输入单输出回归预测
回归预测 | Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的多输入单输出回归预测
目录
- 回归预测 | Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的多输入单输出回归预测
- 预测效果
- 基本介绍
- 程序设计
- 参考资料
预测效果








基本介绍
Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的数据回归预测(完整源码和数据)
1.Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的输入多个特征,输出单个变量,多输入单输出回归预测;
3.多指标评价,评价指标包括:R2、MAE、MSE、RMSE等,代码质量极高;
4.粒子群算法优化参数为:优化核函数超参数 sigma,标准差,初始噪声标准差;
5.excel数据,方便替换,运行环境2018及以上。
程序设计
- 完整程序和数据获取方式(资源处下载):Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的数据回归预测
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% 清空环境变量
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行
% restoredefaultpath
%% 导入数据
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
f_ =size(P_train, 1); %输入特征维度
M = size(P_train, 2);
N = size(P_test, 2);
%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% 转置以适应模型
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% 超参数设置
Best_pos = [0.6, 0.7, 30]; % 优化下界%% 仿真测试
t_sim1 = predict(net, p_train);
t_sim2 = predict(net, p_test );
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% 数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% 数据转置
T_sim1=T_sim1';
T_sim2 =T_sim2';
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% 均方根误差
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2 - T_test ).^2) ./ N);%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%
%决定系数
R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test - T_sim2)^2 / norm(T_test - mean(T_test ))^2;
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%%
%均方误差 MSE
mse1 = sum((T_sim1 - T_train).^2)./M;
mse2 = sum((T_sim2 - T_test).^2)./N;
%%
%RPD 剩余预测残差
SE1=std(T_sim1-T_train);
RPD1=std(T_train)/SE1;
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
SE=std(T_sim2-T_test);
RPD2=std(T_test)/SE;
%% 平均绝对误差MAE
MAE1 = mean(abs(T_train - T_sim1));
MAE2 = mean(abs(T_test - T_sim2));
%% 平均绝对百分比误差MAPE
MAPE1 = mean(abs((T_train - T_sim1)./T_train));
MAPE2 = mean(abs((T_test - T_sim2)./T_test));
%-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
%% 测试集误差图
figure
ERROR3=T_test-T_sim2;
plot(T_test-T_sim2,'b-*','LineWidth',1.5)
xlabel('测试集样本编号')
ylabel('预测误差')
title('测试集预测误差')
grid on;
legend('GPR预测输出误差')
%% 打印出评价指标
disp(['-----------------------误差计算--------------------------'])
disp(['评价结果如下所示:'])
disp(['平均绝对误差MAE为:',num2str(MAE2)])
disp(['均方误差MSE为: ',num2str(mse2)])
disp(['均方根误差RMSEP为: ',num2str(error2)])
disp(['决定系数R^2为: ',num2str(R2)])
disp(['剩余预测残差RPD为: ',num2str(RPD2)])
disp(['平均绝对百分比误差MAPE为: ',num2str(MAPE2)])
参考资料
[1]https://blog.csdn.net/kjm13182345320/article/details/124443069?spm=1001.2014.3001.5501
[2]https://blog.csdn.net/kjm13182345320/article/details/124443735?spm=1001.2014.3001.5501
相关文章:

回归预测 | Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的多输入单输出回归预测
回归预测 | Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的多输入单输出回归预测 目录 回归预测 | Matlab基于CPO-GPR基于冠豪猪算法优化高斯过程回归的多输入单输出回归预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 Matlab基于CPO-GPR基于冠豪猪算法优化高斯…...

python 日期字符串转换为指定格式的日期
在Python编程中,日期处理是一个常见的任务。我们经常需要将日期字符串转换为Python的日期对象,以便进行日期的计算、比较或其他操作。同时,为了满足不同的需求,我们还需要将日期对象转换为指定格式的日期字符串。本文将详细介绍如…...
day03-Docker
1.初识 Docker 1.1.什么是 Docker 1.1.1.应用部署的环境问题 大型项目组件较多,运行环境也较为复杂,部署时会碰到一些问题: 依赖关系复杂,容易出现兼容性问题开发、测试、生产环境有差异 例如一个项目中,部署时需要依…...
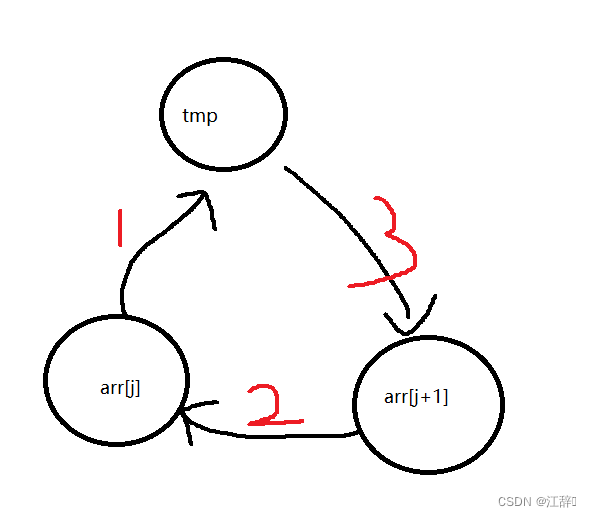
C语言函数实现冒泡排序
前言 今天我们来看看怎么使用函数的方式实现冒泡排序吧,我们以一个数组为例arr[] {9,8,7,6,5,4,3,2,1,0},我们将这个数组通过冒泡排序的方式让他变为升序吧。 代码实现 #include<stdio.h> void bubble_sort(int arr[], int sz) {int i 0;for (i 0;i < s…...
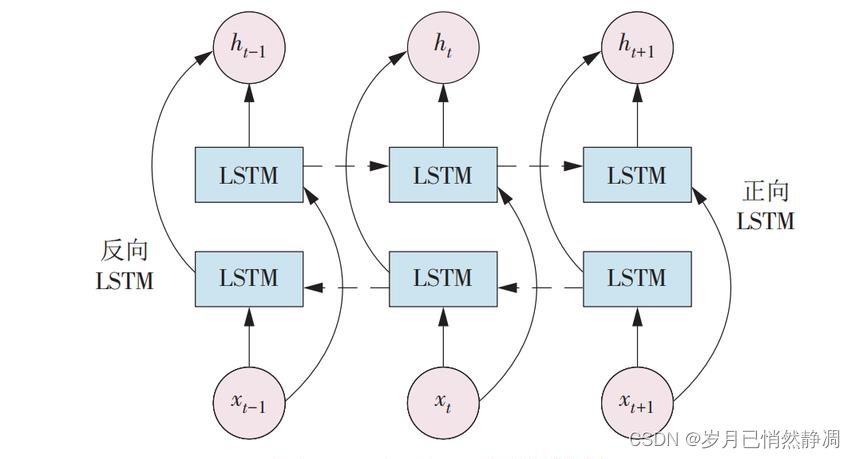
区间概率预测python|QR-CNN-BiLSTM+KDE分位数-卷积-双向长短期记忆神经网络-时间序列区间概率预测+核密度估计
区间预测python|QR-CNN-BiLSTMKDE分位数-卷积-双向长短期记忆神经网络-核密度估计-回归时间序列区间预测 模型输出展示: (图中是只设置了20次迭代的预测结果,宽度较宽,可自行修改迭代参数,获取更窄的预测区间) 注&am…...

Java 分支结构 - if…else/switch
顺序结构只能顺序执行,不能进行判断和选择,因此需要分支结构。 Java有两种分支结构: if语句switch语句 if语句 一个if语句包含一个布尔表达式和一条或多条语句。 语法 If 语句的用语法如下: if(布尔表达式) {//如果布尔表达…...

【Unity每日一记】如何从0到1将特效图集制作成一个特效
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:Uni…...

磁力链接的示例与解释
磁力链接(Magnet URI scheme)是一种特殊类型的统一资源标识符(URI),它包含了通过特定散列函数(如SHA-1)得到的文件内容的散列值,而不是基于位置或名称的引用。这使得磁力链接成为在分…...
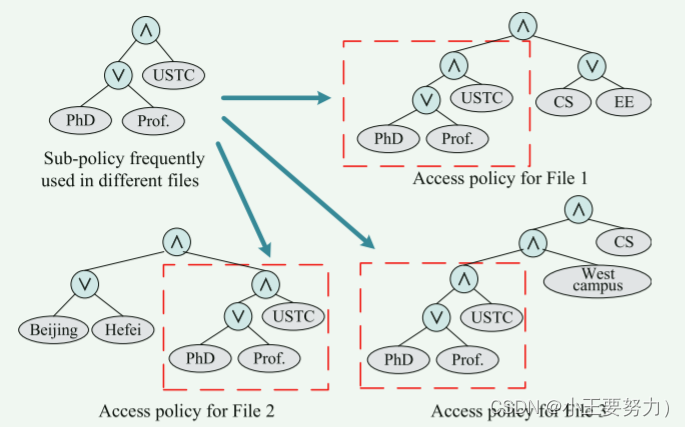
云存储中常用的相同子策略的高效、安全的基于属性的访问控制的论文阅读
参考文献为2022年发表的Efficient and Secure Attribute-Based Access Control With Identical Sub-Policies Frequently Used in Cloud Storage 动机 ABE是实现在云存储中一种很好的访问控制手段,但是其本身的计算开销导致在实际场景中应用收到限制。本论文研究了一种LSSS矩…...

JVM高级篇之GC
文章目录 版权声明垃圾回收器的技术演进ShenandoahShenandoah GC体验Shenandoah GC循环过程 ZGCZGC简介ZGC的版本更迭ZGC体验&使用ZGC的参数设置ZGC的调优 版权声明 本博客的内容基于我个人学习黑马程序员课程的学习笔记整理而成。我特此声明,所有版权属于黑马…...
三国游戏)
第十四届蓝桥杯省赛大学C组(C/C++)三国游戏
原题链接:三国游戏 小蓝正在玩一款游戏。 游戏中魏蜀吴三个国家各自拥有一定数量的士兵 X,Y,Z(一开始可以认为都为 0)。 游戏有 n 个可能会发生的事件,每个事件之间相互独立且最多只会发生一次,当第 i 个事件发生时…...
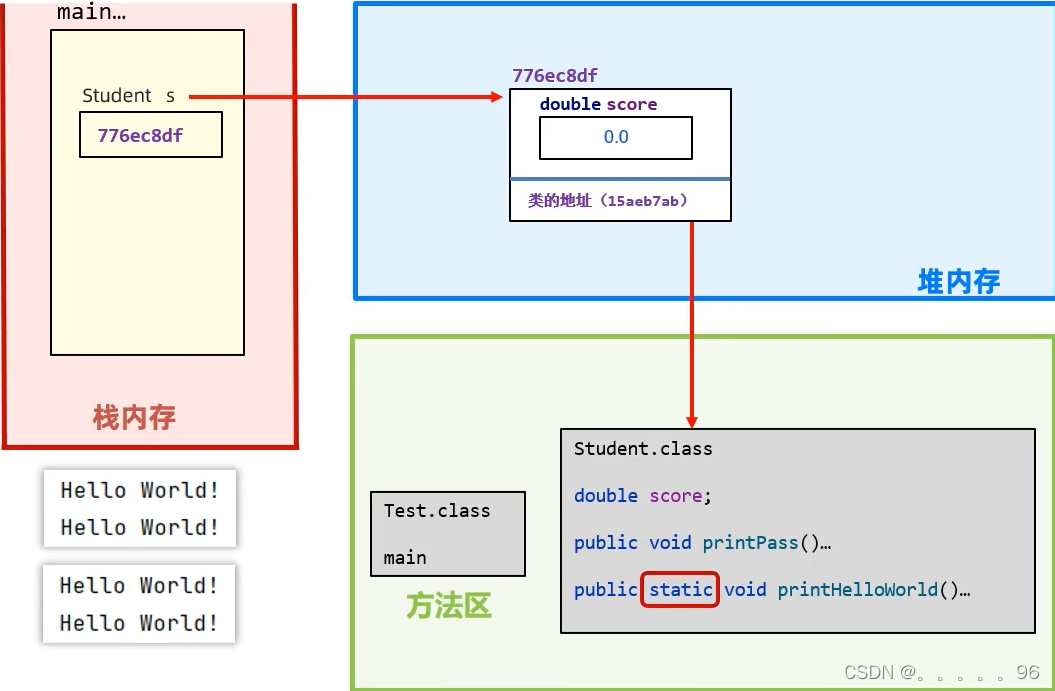
java之static详细总结
static也叫静态,可以修饰成员变量、成员方法。 成员变量 按照有无static分为两种: 类变量:static修饰,属于类,与类一起加载一次,在内存中只有一份,会被类的全部对象共享实例变量(…...
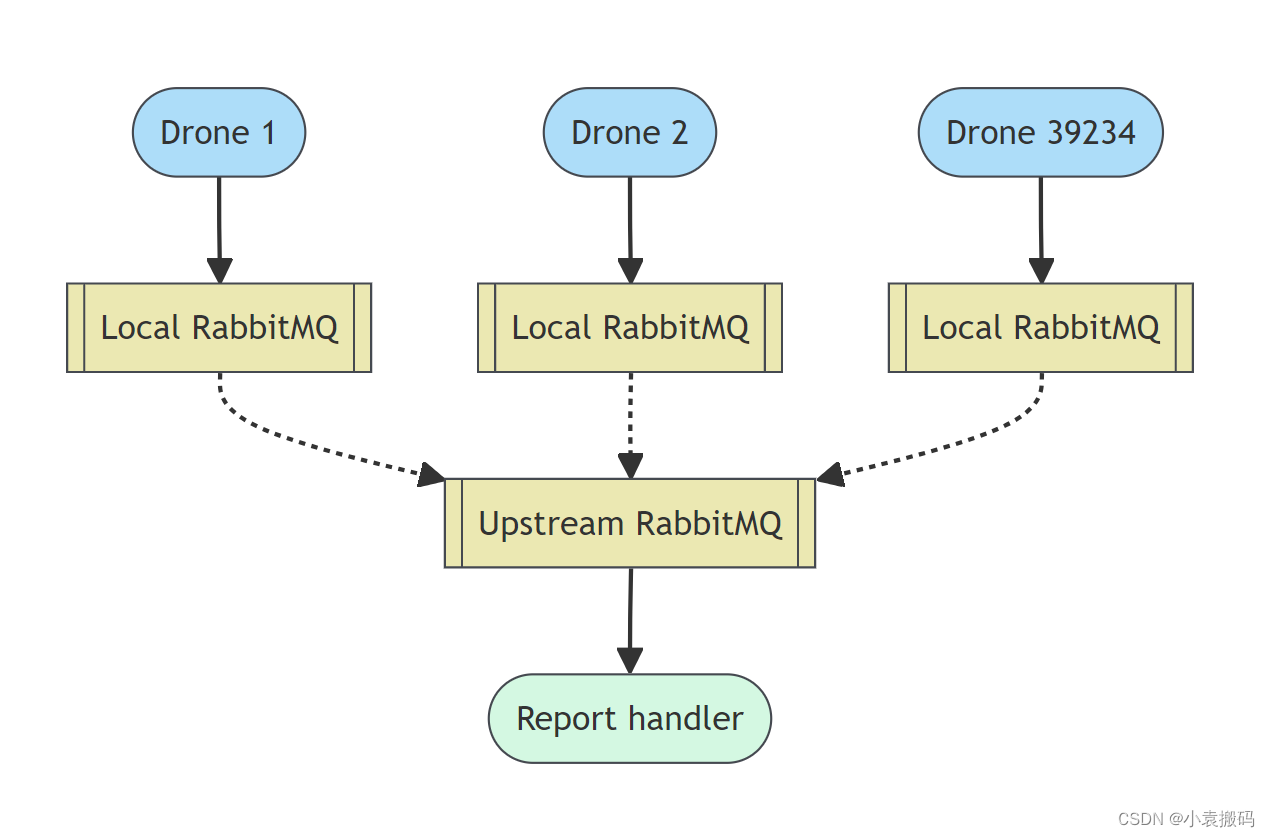
RabbitMQ3.13.x之六_RabbitMQ使用场景
RabbitMQ3.13.x之六_RabbitMQ使用场景 文章目录 RabbitMQ3.13.x之六_RabbitMQ使用场景1. 为什么选择 RabbitMQ?1. 可互操作2. 灵活3. 可靠 2. 常见用户案例1. 服务解耦2. 远程过程调用3. 流处理4. 物联网 1. 为什么选择 RabbitMQ? RabbitMQ 是一个可靠且…...

C++ 类和对象(初篇)
类的引入 C语言中,结构体中只能定义变量,在C中,结构体内不仅可以定义变量,也可以定义函数。 而为了区分C和C我们将结构体重新命名成class去定义 类的定义 标准格式: class className {// 类体:由成员函…...

微软推出GPT-4 Turbo优先使用权:Copilot for Microsoft 365商业用户享受无限制对话及增强图像生成能力
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

Spring Boot Actuator
概述 Spring Boot Actuator是Spring Boot的一个功能模块,用于提供生产环境中常见的监控和管理功能。它提供了各种端点(endpoints),可以用于监视应用程序的运行状况、收集应用程序的指标数据以及与应用程序进行交互。 以下是Spri…...
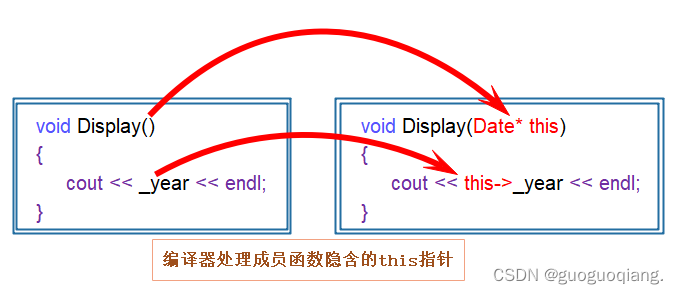
我与C++的爱恋:类与对象(一)
🔥个人主页:guoguoqiang. 🔥专栏:我与C的爱恋 C语言是面向过程的,关注的是过程,分析出求解问题的步骤,通过函数调用逐步解决问题。 C是基于面向对象的,关注的是对象&…...
)
os模块篇(十八)
文章目录 os._exit(n)os.forkpty()os.kill(pid, sig, /)os.killpg(pgid, sig, /)os.nice(increment, /)os.pidfd_open(pid, flags0)os.plock(op, /)os.popen(cmd, moder, buffering-1)os.posix_spawn(path, argv, env, *, file_actionsNone, setpgroupNone, resetidsFalse, set…...

Oracle 数据库工作中常用知识点:sql语法与常用函数
.to_date()函数 to_date函数是Oracle特有的函数,该函数用来做日期转换。 举例: SELECT TO_DATE(‘2006-05-01 19:25:34’, ‘YYYY-MM-DD HH24:MI:SS’) FROM DUAL 日期格式: YYYY、YYY、YY 分别代表4位、3位、2位的数字年 …...

软件工程
开发模型 瀑布模型 用于结构化模型开发 适用需求明确或者二次开发 原型模型 适用需求不明确 演化模型 增量模型 适用需求不明确 先做一块,再做一块,这样不断的对核心功能的审视,降低风险 螺旋模型 由多个模型组合成 适用需求不明…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...

在Spring Boot中集成RabbitMQ的完整指南
前言 在现代微服务架构中,消息队列(Message Queue)是实现异步通信、解耦系统组件的重要工具。RabbitMQ 是一个流行的消息中间件,支持多种消息协议,具有高可靠性和可扩展性。 本博客将详细介绍如何在 Spring Boot 项目…...

Git 命令全流程总结
以下是从初始化到版本控制、查看记录、撤回操作的 Git 命令全流程总结,按操作场景分类整理: 一、初始化与基础操作 操作命令初始化仓库git init添加所有文件到暂存区git add .提交到本地仓库git commit -m "提交描述"首次提交需配置身份git c…...

前端打包工具简单介绍
前端打包工具简单介绍 一、Webpack 架构与插件机制 1. Webpack 架构核心组成 Entry(入口) 指定应用的起点文件,比如 src/index.js。 Module(模块) Webpack 把项目当作模块图,模块可以是 JS、CSS、图片等…...
