Python---Numpy线性代数
1.数组和矩阵操作:
创建数组和矩阵:np.array, np.matrix
基本的数组操作:形状修改、大小调整、转置等
import numpy as np# 创建一个 2x3 的数组
A = np.array([[1, 2, 3], [4, 5, 6]])
print("数组 A:\n", A)# 将数组 A 转换为矩阵
B = np.matrix(A)
print("矩阵 B:\n", B)# 例一:
# 定义两个矩阵 C 和 D
C = np.array([[1, 2], [3, 4]])
D = np.array([[5, 6], [7, 8]])# 进行矩阵乘法
result = np.dot(C, D)
print("矩阵乘法结果:\n", result)# 例二:
x1 = np.array([[1, 2, 3], [4, 5, 6]])x2 = np.array([[1, 2], [3, 4],[5, 6]])# 矩阵乘法
print(x1.dot(x2))# 计算对角线之和
print(x2.trace())
2.线性代数运算:
矩阵乘法:np.dot, np.matmul
内积和外积:np.inner, np.outer
点积:np.dot (对于一维数组)
对角线之和:np.trace()
# 定义系数矩阵和常数向量
coefficients = np.array([[3, 1], [1, 2]])
constants = np.array([9, 8])# 求解线性方程组
solution = np.linalg.solve(coefficients, constants)
print("线性方程组的解:\n", solution)3.特征值和特征向量:
计算矩阵的特征值和特征向量:np.linalg.eig
特征值分解:np.linalg.eigvalsh, np.linalg.eigh
# 定义一个需要计算特征值和特征向量的矩阵
E = np.array([[1, 2], [2, 1]])# 计算特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(E)
print("特征值:\n", eigenvalues)
print("特征向量:\n", eigenvectors)4.矩阵分解:
奇异值分解(SVD):np.linalg.svd
卢分解(LU):np.linalg.lu
特征值分解(如前所述)
# 定义一个用于奇异值分解的矩阵
F = np.array([[2, 3], [4, 5]])# 进行奇异值分解
U, S, VT = np.linalg.svd(F)
print("U 矩阵:\n", U)
print("奇异值:\n", S)
print("VT 矩阵:\n", VT)5.线性方程组求解:
解决线性方程组:np.linalg.solve
计算矩阵的逆:np.linalg.inv
# 定义一个矩阵
G = np.array([[1, 2], [3, 4]])# 计算行列式
det_G = np.linalg.det(G)
print("矩阵 G 的行列式:\n", det_G)# 计算矩阵的迹
trace_G = np.trace(G)
print("矩阵 G 的迹:\n", trace_G)
6.行列式和迹:
计算矩阵的行列式:np.linalg.det
计算矩阵的迹:np.trace
# 创建一个 3x3 矩阵
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])# 计算矩阵的行列式
det_value = np.linalg.det(matrix)
print("矩阵的行列式为:", det_value)
# 使用之前定义的矩阵
trace_value = np.trace(matrix)
print("矩阵的迹为:", trace_value)7.范数和条件数:
计算向量的范数:np.linalg.norm
计算矩阵的条件数:np.linalg.cond
# 定义一个向量
vector = np.array([3, 4])# 计算向量的 L2 范数
norm = np.linalg.norm(vector)
print("向量的 L2 范数:\n", norm)8.三角函数和相关函数:
正弦、余弦等三角函数:np.sin, np.cos 等
反三角函数:np.arcsin, np.arccos 等
# 定义一个包含两个元素的数组,代表角度(以弧度为单位)
angles = np.array([0, np.pi / 2])# 计算正弦和余弦值
sine_values = np.sin(angles)
cosine_values = np.cos(angles)print("角度的正弦值:", sine_values)
print("角度的余弦值:", cosine_values)# 定义一个包含两个元素的数组,代表正弦和余弦值
sine_cosine_values = np.array([np.sin(np.pi / 4), np.cos(np.pi / 4)])# 计算反正弦和反余弦值
arc_sine_value = np.arcsin(sine_cosine_values[0])
arc_cosine_value = np.arccos(sine_cosine_values[1])print("反正弦值:", arc_sine_value)
print("反余弦值:", arc_cosine_value)
相关文章:

Python---Numpy线性代数
1.数组和矩阵操作: 创建数组和矩阵:np.array, np.matrix 基本的数组操作:形状修改、大小调整、转置等 import numpy as np# 创建一个 2x3 的数组 A np.array([[1, 2, 3], [4, 5, 6]]) print("数组 A:\n", A)# 将数组 A 转换为矩阵…...

react+ echarts 轮播饼图
react echarts 轮播饼图 图片示例 代码 import * as echarts from echarts; import { useEffect } from react; import styles from ./styles.scss;const Student (props) > {const { dataList, title } props;// 过滤数据const visionList [{ value: 1048, name: Se…...
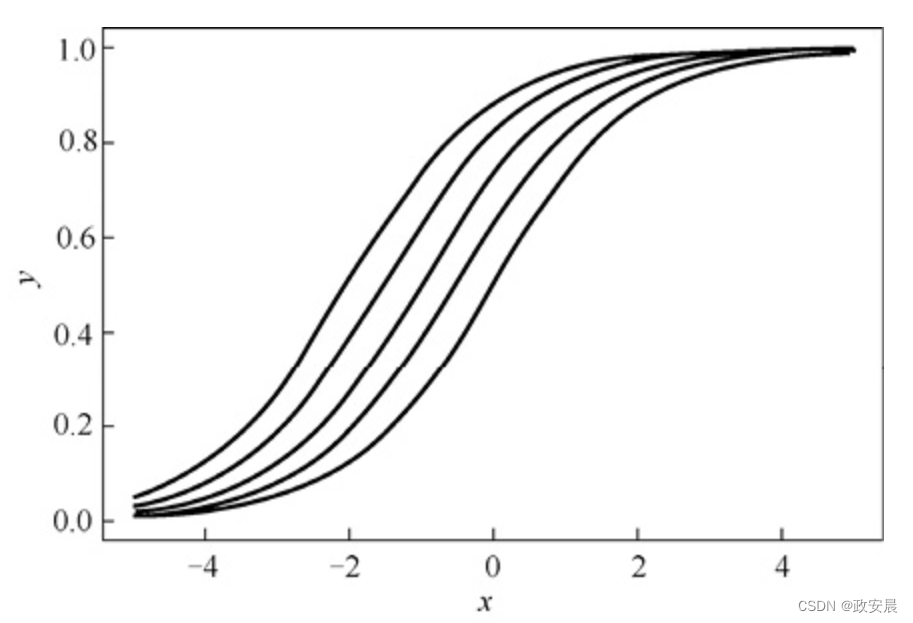
政安晨:【深度学习神经网络基础】(三)—— 激活函数
目录 线性激活函数 阶跃激活函数 S型激活函数 双曲正切激活函数 修正线性单元 Softmax激活函数 偏置扮演什么角色? 政安晨的个人主页:政安晨 欢迎 👍点赞✍评论⭐收藏 收录专栏: 政安晨的机器学习笔记 希望政安晨的博客能够对您有所裨…...
使用tomcat里的API - servlet 写动态网页
一、创建一个新的Maven空项目 首次创建maven项目的时候,会自动从maven网站上下载一些依赖组件(这个过程需要保证网络稳定,否则后续打包一些操作会出现一些问题) ps:校园网可能会屏蔽一些网站,可能会导致maven的依赖…...
从0到1搭建文档库——sphinx + git + read the docs
sphinx git read the docs 目录 一、sphinx 1 sphinx的安装 2 本地构建文件框架 1)创建基本框架(生成index.rst ;conf.py) conf.py默认内容 index.rst默认内容 2)生成页面(Windows系统下…...

EasyExcel 校验后导入
引入pom <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.3.3</version></dependency>触发校验类 import com.baomidou.mybatisplus.extension.api.R; import lombok.experimental…...

【星计划★C语言】c语言初相识:探索编程之路
🌈个人主页:聆风吟_ 🔥系列专栏:星计划★C语言、Linux实践室 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. ⛳️第一个c语言程序二. ⛳️数据类型2.1 🔔数据单位2.2 &…...

搜维尔科技:借助 ARVR 的力量缩小现代制造业的技能差距
借助ARVR的力量缩小现代制造业的技能差距 搜维尔科技:Senseglove案例-扩展机器人技术及其VR应用...
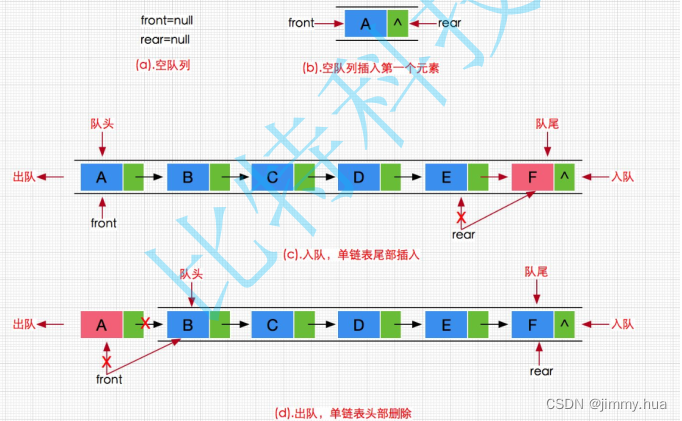
数据结构之栈和队列
1.前言 大家好久不见,这段时间由于忙去了。就没有即使维护我的博客,先给大家赔个不是。 我们还是规矩不乱,先赞后看~ 今天讲的内容是数据结构中非常重要的一个部分:栈和队列。它在今后的学习中也会再次出现(c&#…...
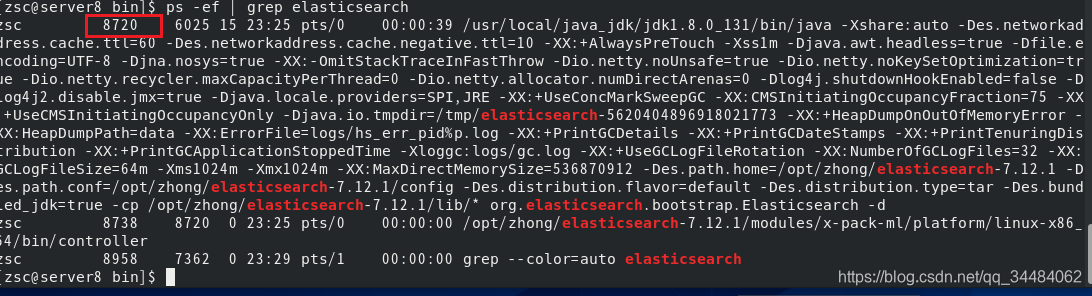
centos安装使用elasticsearch
1.首先可以在 Elasticsearch 官网 Download Elasticsearch | Elastic 下载安装包 2. 在指定的位置(我的是/opt/zhong/)解压安装包 tar -zxvf elasticsearch-7.12.1-linux-x86_64.tar.gz 3.启动es-这种方式启动会将日志全部打印在当前页面,一旦使用 ctrlc退出就会导…...
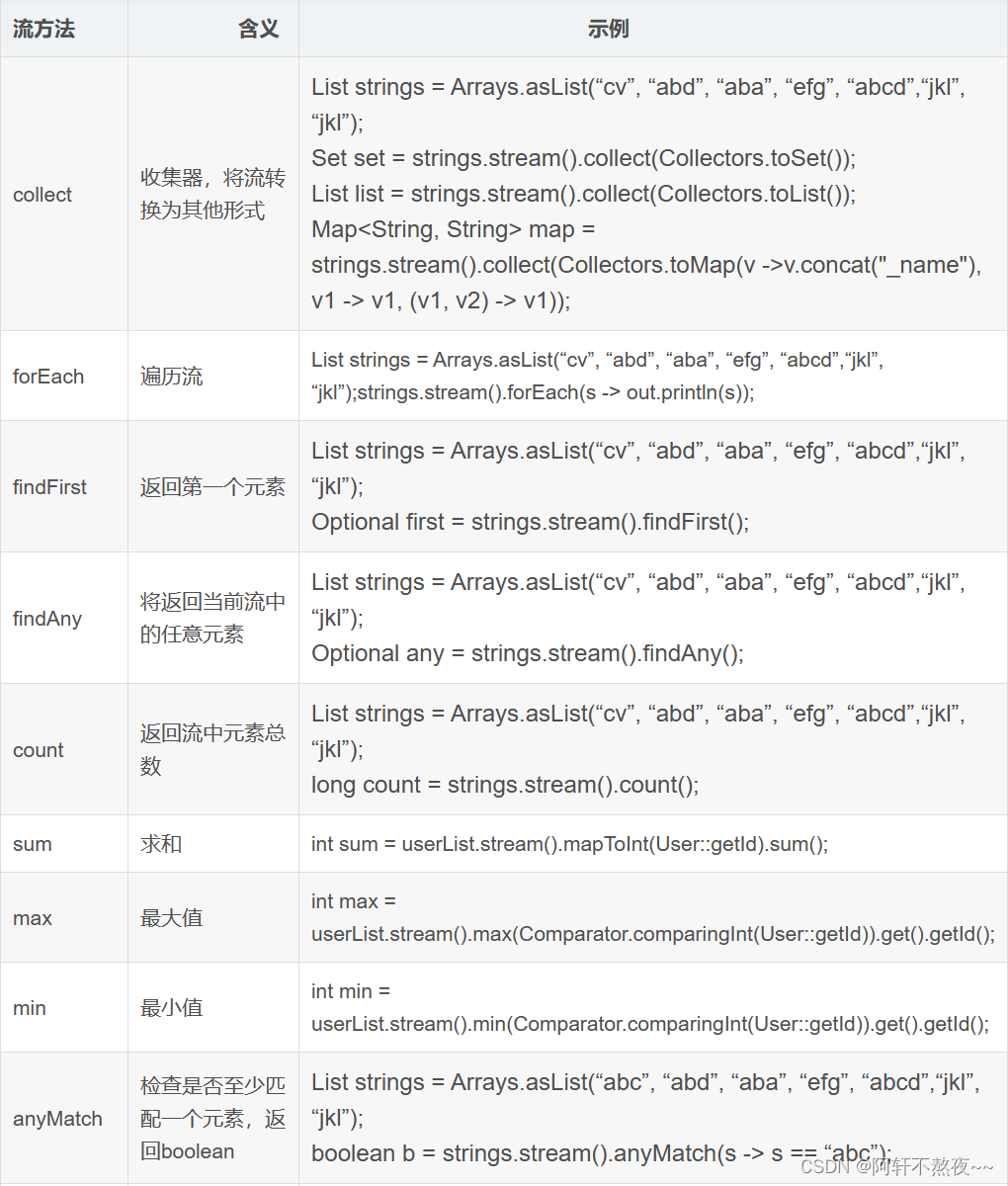
4.7学习总结
java学习 一.Stream流 (一.)概念: Stream将要处理的元素集合看作一种流,在流的过程中,借助Stream API对流中的元素进行操作,比如:筛选、排序、聚合等。Stream流是对集合(Collection)对象功能的增强&…...
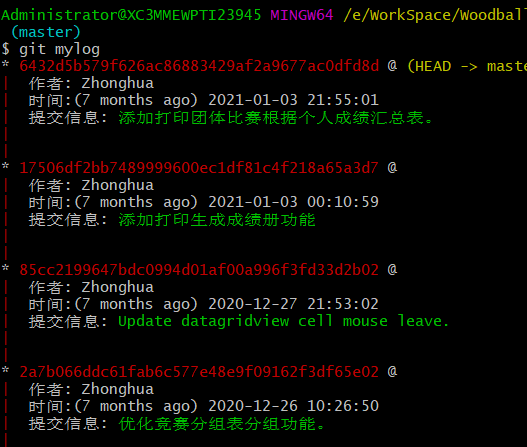
自定义gitlog格式
git log命令非常强大而好用,在复杂系统的版本管理中扮演着重要的角色,但默认的git log命令显示出的东西实在太丑,不好好打扮一下根本没法见人,打扮好了用alias命令拍个照片,就正式出道了! 在使用git查看lo…...

Redission--分布式锁
Redission的锁的好处 Redission分布式锁的底层是setnx和lua脚本(保证原子性) 1.是可重入锁。 2.Redisson 锁支持自动续期功能,这可以帮助我们合理控制分布式锁的有效时长,当业务逻辑执行时间超出了锁的过期时间,锁会自动续期,避免…...

非关系型数据库(缓存数据库)redis的集群
目录 一.群集模式——Cluster 1.原理 2.作用 3.特点 4.工作机制 哈希槽 哈希槽的分配 哈希槽可按照集群主机数平均分配(默认分配) 根据主机的性能以及功能自定义分配 redis集群的分片 分片 如何找到给定key的分片 优势 二. 搭建Redis群集…...
)
MySQL:表的约束(上)
文章目录 空属性默认值列描述zerofill主键 本篇总结的是MySQL中关于表的约束部分的内容 空属性 在进行表的创建时,会有两个值,null和not null,而数据库默认的字段基本都是空,但是在实际的开发过程中要保证字段不能为空ÿ…...
树莓派5使用体验
原文地址:树莓派5使用体验 - Pleasure的博客 下面是正文内容: 前言 好久没有关于教程方面的博文了,由于最近打算入门嵌入式系统,所以就去购入了树莓派5开发板 树莓派5是2023年10月23日正式发售的,过去的时间不算太远吧…...

代码随想录算法训练营第42天| 背包问题、416. 分割等和子集
01 背包 题目描述:有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 二维dp数组01背包: 确定dp数组以及下标的含义 …...

Node.js安装及环境配置指南
Node.js安装及环境配置指南 一、Node.js的安装 安装Node.js之前,首先需要确保你的电脑已经安装了合适的编译器和开发环境。Node.js是一个开源的、跨平台的JavaScript运行环境,它使得JavaScript可以在服务器端运行。 下载Node.js安装包 访问Node.js的…...
【Java基础】面试题汇总
Java基础面试题1. JVM vs JDK vs JRE 2. 什么是字节码?采用字节码的好处是什么?3. 为什么说 Java 语言“编译与解释并存”?4. AOT 有什么优点?为什么不全部使用 AOT 呢?5. Java 和 C 的区别?6. Java 中的基本数据类型࿱…...
)
数据库事务的超级详细讲解,包括事务特性、事务隔离级别、MVCC(多版本并发控制)
数据库事务: 主要有事务特性,事务的隔离级别,MVCC。 事务特性: 事务(Transaction)是指作为单个逻辑工作单元执行的一系列操作,这些操作要么全部成功执行,要么全部不执行ÿ…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
