轨迹规划 | 图解最优控制LQR算法(附ROS C++/Python/Matlab仿真)
目录
- 0 专栏介绍
- 1 最优控制理论
- 2 线性二次型问题
- 3 LQR的价值迭代推导
- 4 基于差速模型的LQR控制
- 5 仿真实现
- 5.1 ROS C++实现
- 5.2 Python实现
- 5.3 Matlab实现
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 最优控制理论
最优控制理论是一种数学和工程领域的理论,旨在寻找如何使系统在给定约束条件下达到最佳性能的方法。它的基本思想是通过选择合适的控制输入,以最小化或最大化某个性能指标来优化系统的行为。其中,系统的动态行为通常用状态方程描述,状态表示系统在某一时刻的内部状态。状态空间表示将系统的状态和控制输入表示为向量,通常用微分方程或差分方程来描述系统的演化。在最优控制理论中,会设置代价函数或者目标函数,用来衡量系统行为的好坏的函数。性能指标可以是各种形式,如最小化路径长度、最小化能量消耗、最大化系统稳定性等。最优控制理论在许多领域都有广泛的应用,包括航空航天、机器人学、经济学、生态学等。
2 线性二次型问题
若系统动力学特性可以用一组线性微分方程表示,且性能指标为状态变量和控制变量的二次型函数,则此类最优控制问题称为线性二次型问题。线性二次调节器(Linear Quadratic Regulator, LQR)是求解线性二次型问题常用的求解方法之一,其假设系统零输入且期望状态为零。

如图所示的全状态反馈控制系统。设控制误差 x k = z k − z k ∗ \boldsymbol{x}_k=\boldsymbol{z}_k-\boldsymbol{z}_{k}^{*} xk=zk−zk∗,其中 z k \boldsymbol{z}_k zk、 z k ∗ \boldsymbol{z}_{k}^{*} zk∗分别是第 k k k个控制时间步的实际状态和期望状态,则全反馈控制律由误差驱动
v k = v k ∗ − K x k ⇔ u = v − v ∗ u k = − K x k \boldsymbol{v}_k=\boldsymbol{v}_{k}^{*}-\boldsymbol{Kx}_k\xLeftrightarrow{\boldsymbol{u}=\boldsymbol{v}-\boldsymbol{v}^*}\boldsymbol{u}_k=-\boldsymbol{Kx}_k vk=vk∗−Kxku=v−v∗ uk=−Kxk
上式表明可以通过选取状态变量和输入变量,使系统等效为零输入(跟踪期望输入)且期望状态为零(消除状态误差),满足应用LQR进行最优控制的条件。定义代价函数
J = ∑ k = 0 N ( x k T Q x k + u k T R u k ) J=\sum_{k=0}^N{\left( \boldsymbol{x}_{k}^{T}\boldsymbol{Qx}_k+\boldsymbol{u}_{k}^{T}\boldsymbol{Ru}_k \right)} J=k=0∑N(xkTQxk+ukTRuk)
其中 Q \boldsymbol{Q} Q与 R \boldsymbol{R} R是用户设定的半正定矩阵,前者衡量了系统状态向期望轨迹的收敛速度,后者衡量了系统能量消耗的相对大小,二者互相制约——希望系统快速收敛往往需要加强控制力度,导致能量耗散。因此, 与 需要结合具体场景进行调节。
3 LQR的价值迭代推导
针对 J J J进行优化,引入价值迭代策略,价值迭代的理论基础请看Pytorch深度强化学习1-4:策略改进定理与贝尔曼最优方程详细推导
J k ( x k , u k ) = min u k [ x k T Q x k + u k T R u k + J k + 1 ( x k + 1 ) ] J_k\left( \boldsymbol{x}_k,\boldsymbol{u}_k \right) =\underset{\boldsymbol{u}_k}{\min}\left[ \boldsymbol{x}_{k}^{T}\boldsymbol{Qx}_k+\boldsymbol{u}_{k}^{T}\boldsymbol{Ru}_k+J_{k+1}\left( \boldsymbol{x}_{k+1} \right) \right] Jk(xk,uk)=ukmin[xkTQxk+ukTRuk+Jk+1(xk+1)]
即第 k k k步到终端的代价等于当前步的代价与第 k + 1 k+1 k+1步到终端的代价之和。根据 J J J的定义,其一定能表示成二次型 J k = x k T P k x k J_k=\boldsymbol{x}_{k}^{T}\boldsymbol{P}_k\boldsymbol{x}_k Jk=xkTPkxk,对于优化问题 u k = a r g min u k J k ( x k , u k ) \boldsymbol{u}_k=\mathrm{arg}\min _{\boldsymbol{u}_k}J_k\left( \boldsymbol{x}_k,\boldsymbol{u}_k \right) uk=argminukJk(xk,uk),令
∂ J k ( x k , u k ) ∂ u k = ∂ ∂ u k ( x k T P k x k + u k T R u k + J k + 1 ( A x k + B u k ) ) = ∂ ∂ u k ( u k T R u k + ( A x k + B u k ) T P k + 1 ( A x k + B u k ) ) = 2 ( R + B T P k + 1 B ) u k + 2 B T P k + 1 A x k = 0 \begin{aligned}\frac{\partial J_k\left( \boldsymbol{x}_k,\boldsymbol{u}_k \right)}{\partial \boldsymbol{u}_k}&=\frac{\partial}{\partial \boldsymbol{u}_k}\left( \boldsymbol{x}_{k}^{T}\boldsymbol{P}_k\boldsymbol{x}_k+\boldsymbol{u}_{k}^{T}\boldsymbol{Ru}_k+J_{k+1}\left( \boldsymbol{Ax}_k+\boldsymbol{Bu}_k \right) \right) \\&=\frac{\partial}{\partial \boldsymbol{u}_k}\left( \boldsymbol{u}_{k}^{T}\boldsymbol{Ru}_k+\left( \boldsymbol{Ax}_k+\boldsymbol{Bu}_k \right) ^T\boldsymbol{P}_{k+1}\left( \boldsymbol{Ax}_k+\boldsymbol{Bu}_k \right) \right) \\&=2\left( \boldsymbol{R}+\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{B} \right) \boldsymbol{u}_k+2\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{Ax}_k\\&=0\end{aligned} ∂uk∂Jk(xk,uk)=∂uk∂(xkTPkxk+ukTRuk+Jk+1(Axk+Buk))=∂uk∂(ukTRuk+(Axk+Buk)TPk+1(Axk+Buk))=2(R+BTPk+1B)uk+2BTPk+1Axk=0
则 u k ∗ = − ( R + B T P k + 1 B ) − 1 B T P k + 1 A x k \boldsymbol{u}_{k}^{*}=-\left( \boldsymbol{R}+\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{B} \right) ^{-1}\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{Ax}_k uk∗=−(R+BTPk+1B)−1BTPk+1Axk,对比 u k = − K x k \boldsymbol{u}_k=-\boldsymbol{Kx}_k uk=−Kxk可得
K k = ( R + B T P k + 1 B ) − 1 B T P k + 1 A \boldsymbol{K}_k=\left( \boldsymbol{R}+\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{B} \right) ^{-1}\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{A} Kk=(R+BTPk+1B)−1BTPk+1A
将 u k = − K x k \boldsymbol{u}_k=-\boldsymbol{Kx}_k uk=−Kxk代入 J k J_k Jk可得
J k = x k T P k x k = x k T ( Q + K k T R K k + ( A − B K k ) P k + 1 ( A − B K k ) ) x k J_k=\boldsymbol{x}_{k}^{T}\boldsymbol{P}_k\boldsymbol{x}_k=\boldsymbol{x}_{k}^{T}\left( \boldsymbol{Q}+\boldsymbol{K}_{k}^{T}\boldsymbol{RK}_k+\left( \boldsymbol{A}-\boldsymbol{BK}_k \right) \boldsymbol{P}_{k+1}\left( \boldsymbol{A}-\boldsymbol{BK}_k \right) \right) \boldsymbol{x}_k Jk=xkTPkxk=xkT(Q+KkTRKk+(A−BKk)Pk+1(A−BKk))xk
从而
P k = Q + A T P k + 1 A − A T P k + 1 B ( R + B T P k + 1 B ) − 1 B T P k + 1 A \boldsymbol{P}_k=\boldsymbol{Q}+\boldsymbol{A}^T\boldsymbol{P}_{k+1}\boldsymbol{A}-\boldsymbol{A}^T\boldsymbol{P}_{k+1}\boldsymbol{B}\left( \boldsymbol{R}+\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{B} \right) ^{-1}\boldsymbol{B}^T\boldsymbol{P}_{k+1}\boldsymbol{A} Pk=Q+ATPk+1A−ATPk+1B(R+BTPk+1B)−1BTPk+1A
称为离散迭代黎卡提方程。根据贝尔曼最优原理,在迭代过程中 P k \boldsymbol{P}_k Pk会逐步收敛。
4 基于差速模型的LQR控制
根据差分机器人运动学模型
p ˙ = [ x ˙ y ˙ θ ˙ ] = [ v cos θ v sin θ ω ] = [ f 1 f 2 f 3 ] \boldsymbol{\dot{p}}=\left[ \begin{array}{c} \dot{x}\\ \dot{y}\\ \dot{\theta}\\\end{array} \right] =\left[ \begin{array}{c} v\cos \theta\\ v\sin \theta\\ \omega\\\end{array} \right] =\left[ \begin{array}{c} f_1\\ f_2\\ f_3\\\end{array} \right] p˙= x˙y˙θ˙ = vcosθvsinθω = f1f2f3
选择状态量 p = [ x y θ ] T \boldsymbol{p}=\left[ \begin{matrix} x& y& \theta\\\end{matrix} \right] ^T p=[xyθ]T和状态误差量 x = [ x − x r y − y r θ − θ r ] T \boldsymbol{x}=\left[ \begin{matrix} x-x_r& y-y_r& \theta -\theta _r\\\end{matrix} \right] ^T x=[x−xry−yrθ−θr]T,控制量 s = [ v ω ] T \boldsymbol{s}=\left[ \begin{matrix} v& \omega\\\end{matrix} \right] ^T s=[vω]T和控制误差量 u = [ v − v r ω − ω r ] T \boldsymbol{u}=\left[ \begin{matrix} v-v_r& \omega -\omega _r\\\end{matrix} \right] ^T u=[v−vrω−ωr]T,可得
x ( k + 1 ) = ( T A + I ) x ( k ) + T B u ( k ) \boldsymbol{x}\left( k+1 \right) =\left( T\boldsymbol{A}+\boldsymbol{I} \right) \boldsymbol{x}\left( k \right) +T\boldsymbol{Bu}\left( k \right) x(k+1)=(TA+I)x(k)+TBu(k)
其中
A = [ 0 0 − v r sin θ r 0 0 v r cos θ r 0 0 0 ] , B = [ cos θ r 0 sin θ r 0 0 1 ] \boldsymbol{A}=\left[ \begin{matrix} 0& 0& -v_r\sin \theta _r\\ 0& 0& v_r\cos \theta _r\\ 0& 0& 0\\\end{matrix} \right] , \boldsymbol{B}=\left[ \begin{matrix} \cos \theta _r& 0\\ \sin \theta _r& 0\\ 0& 1\\\end{matrix} \right] A= 000000−vrsinθrvrcosθr0 ,B= cosθrsinθr0001
接着按照LQR算法求解即可。
5 仿真实现
5.1 ROS C++实现
核心代码如下所示
Eigen::Vector2d LQRPlanner::_lqrControl(Eigen::Vector3d s, Eigen::Vector3d s_d, Eigen::Vector2d u_r)
{Eigen::Vector2d u;Eigen::Vector3d e(s - s_d);e[2] = regularizeAngle(e[2]);// state equation on errorEigen::Matrix3d A = Eigen::Matrix3d::Identity();A(0, 2) = -u_r[0] * sin(s_d[2]) * d_t_;A(1, 2) = u_r[0] * cos(s_d[2]) * d_t_;Eigen::MatrixXd B = Eigen::MatrixXd::Zero(3, 2);B(0, 0) = cos(s_d[2]) * d_t_;B(1, 0) = sin(s_d[2]) * d_t_;B(2, 1) = d_t_;// discrete iteration Ricatti equationEigen::Matrix3d P, P_;P = Q_;for (int i = 0; i < max_iter_; ++i){Eigen::Matrix2d temp = R_ + B.transpose() * P * B;P_ = Q_ + A.transpose() * P * A - A.transpose() * P * B * temp.inverse() * B.transpose() * P * A;if ((P - P_).array().abs().maxCoeff() < eps_iter_)break;P = P_;}// feedbackEigen::MatrixXd K = -(R_ + B.transpose() * P_ * B).inverse() * B.transpose() * P_ * A;u = u_r + K * e;return u;
}

5.2 Python实现
核心代码如下所示
def lqrControl(self, s: tuple, s_d: tuple, u_r: tuple) -> np.ndarray:dt = self.params["TIME_STEP"]# state equation on errorA = np.identity(3)A[0, 2] = -u_r[0] * np.sin(s_d[2]) * dtA[1, 2] = u_r[0] * np.cos(s_d[2]) * dtB = np.zeros((3, 2))B[0, 0] = np.cos(s_d[2]) * dtB[1, 0] = np.sin(s_d[2]) * dtB[2, 1] = dt# discrete iteration Ricatti equationP, P_ = np.zeros((3, 3)), np.zeros((3, 3))P = self.Q# iterationfor _ in range(self.lqr_iteration):P_ = self.Q + A.T @ P @ A - A.T @ P @ B @ np.linalg.inv(self.R + B.T @ P @ B) @ B.T @ P @ Aif np.max(P - P_) < self.eps_iter:breakP = P_# feedbackK = -np.linalg.inv(self.R + B.T @ P_ @ B) @ B.T @ P_ @ Ae = np.array([[s[0] - s_d[0]], [s[1] - s_d[1]], [self.regularizeAngle(s[2] - s_d[2])]])u = np.array([[u_r[0]], [u_r[1]]]) + K @ ereturn np.array([[self.linearRegularization(float(u[0]))], [self.angularRegularization(float(u[1]))]])

5.3 Matlab实现
核心代码如下所示
function u = lqrControl(s, s_d, u_r, robot, param)dt = param.dt;% state equation on errorA = eye(3);A(1, 3) = -u_r(1) * sin(s_d(3)) * dt;A(2, 3) = u_r(1) * cos(s_d(3)) * dt;B = zeros(3, 2);B(1, 1) = cos(s_d(3)) * dt;B(2, 1) = sin(s_d(3)) * dt;B(3, 2) = dt;% discrete iteration Ricatti equationP = param.Q;% iterationfor i=1:param.lqr_iterationP_ = param.Q + A' * P * A - A' * P * B / (param.R + B' * P * B) * B' * P * A;if max(P - P_) < param.eps_iterbreak;endP = P_;end% feedbackK = -inv(param.R + B' * P_ * B) * B' * P_ * A;e = [s(1) - s_d(1); s(2) - s_d(2); regularizeAngle(s(3) - s_d(3))];u = [u_r(1); u_r(2)] + K * e;u = [linearRegularization(robot, u(1), param), angularRegularization(robot, u(2), param)];
end

完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

轨迹规划 | 图解最优控制LQR算法(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 最优控制理论2 线性二次型问题3 LQR的价值迭代推导4 基于差速模型的LQR控制5 仿真实现5.1 ROS C实现5.2 Python实现5.3 Matlab实现 0 专栏介绍 🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全…...
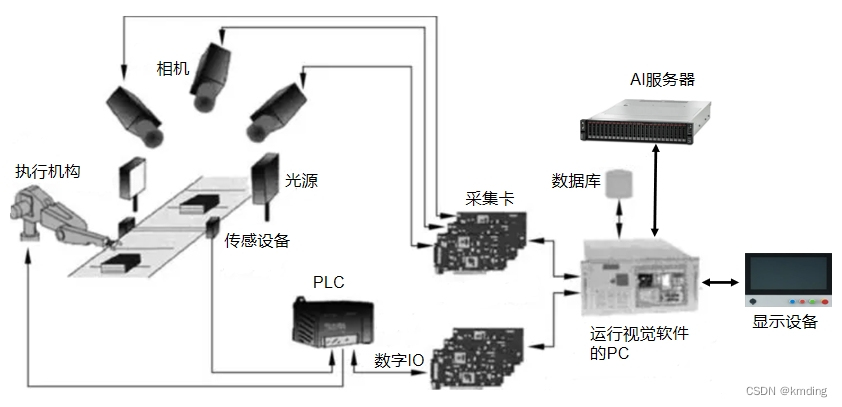
工业视觉检测
目录 我对工业视觉检测的了解 一、关键组成部分 二、应用场景 三、技术挑战 我对工业视觉检测的了解 工业视觉检测是利用机器视觉技术对产品质量进行自动化检查的过程,它在制造业中扮演着至关重要的角色,用于确保产品质量、提高生产效率、减少人工成…...

wheeltec轮趣ROS教育机器人的网络连接
一、术语解析 宿主机:宿主机是指物理主机,比如用于开发测试的笔记本电脑和台式机电脑。 虚拟机:虚拟机是指安装在宿主机的VMware,推荐在宿主机上安装虚拟机,官方提供虚拟机的镜像以及配套的开发环境。 ROS主机&…...
【Linux ARM 裸机】开发环境搭建
1、Ubuntu 和 Windows 文件互传 使用过程中,要频繁进行 Ubuntu 和 Windows 的文件互传,需要使用 FTP 服务; 1.1、开启 Ubuntu 下的 FTP 服务 //安装 FTP 服务 sudo apt-get install vsftpd //修改配置文件 sudo vi /etc/vsftpd.conf//重启…...

怎么保证缓存与数据库的最终一致性?
目录 零.读数据的标准操作 一.Cache aside Patten--旁路模式 二.Read/Write Through Pattern--读写穿透 三.Write Back Pattern--写回 四.运用canal监听mysql的binlog实现缓存同步 零.读数据的标准操作 这里想说的是不管哪种模式读操作都是一样的,这是一种统一…...
免费SSL通配符证书/SSL泛域名证书获取教程
我们先基本了解什么是SSL证书以及其作用。SSL证书是一种数字证书,它通过为网站提供身份验证和数据加密服务,从而保护网站的用户信息安全。当我们在浏览器的地址栏看到“https”和绿色锁标志时,就表示该网站使用了SSL证书。 那么什么又是通配…...

mysql结构与sql执行流程
Mysql的大体结构 客户端:用于链接mysql的软件 连接池: sql接口: 查询解析器: MySQL连接层 连接层: 应用程序通过接口(如odbc,jdbc)来连接mysql,最先连接处理的是连接层。 连接层…...
vue快速入门(十二)v-key索引标志
注释很详细,直接上代码 新增内容 v-key的使用场景数组筛选器的使用 源码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-…...

智能网联汽车自动驾驶数据记录系统DSSAD数据配置
目录 第一章 数据配置一般要求 第二章 数据配置文件中的文件描述 第三章 数据配置文件中的数据描述 第四章 数据配置文件中的数据字典 表A.1 数据字典格式定义 第一章 数据配置一般要求 数据配置文件数据内容应为可读的十进制数据。 数据配置文件应以文件的形式存储在自动驾驶…...

linux知识点
绝对路径用什么符号表示?当前目录、上层目录用什么表示?主目录用什么表示? 切换目录用什么命令 绝对路径: 如/etc/init.d当前目录和上层目录: ./ …/主目录: ~/切换目录: cd 怎么查看当前进程?…...

微信小程序实现滚动标签
使用scroll-view标签可实现组件滚动标签 1、list中 list.wxml代码如下: <!--pages/list/list.wxml--> <navigation-bartitle"小程序" back"{{false}}"color"black" background"#FFF"></navigation-bar><scroll-…...

大语言模型上下文窗口初探(下)
由于篇幅原因,本文分为上下两篇,上篇主要讲解上下文窗口的概念、在LLM中的重要性,下篇主要讲解长文本能否成为LLM的护城河、国外大厂对长文本的态度。 3、长文本是护城河吗? 毫无疑问,Kimi从一开始就用“长文本”占领…...

Java整合ElasticSearch8.13
1、引入Jar包 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-elasticsearch</artifactId> </dependency> 2、配置ES连接信息 spring:elasticsearch:# 地址uris: http://xxx:9200# 用户…...
2.网络编程-HTTP和HTTPS
目录 HTTP介绍 HTTP协议主要组成部分 GET 和 POST有什么区别 常见的 HTTP 状态码有哪些 http状态码100 HTTP1.1 和 HTTP1.0 的区别有哪些 HTTPS 和 HTTP 的区别是什么 HTTP2 和 HTTP1.1 的区别是什么 HTTP3 和 HTTP2 的区别是什么 HTTPS的请求过程 对称加密和非对称…...
MTK i500p AIoT解决方案
一、方案概述 i500p是一款强大而高效的AIoT平台,专为便携式、家用或商用物联网应用而设计,这些应用通常需要大量的边缘计算,需要强大的多媒体功能和多任务操作系统。该平台集成了Arm Cortex-A73 和 Cortex-A53 的四核集群,工作频…...

ES入门十四:分词器
我们存储到ES中数据大致分为以下两种: 全文本,例如文章内容、通知内容精确值,如实体Id 在对这两类值进行查询的时候,精确值类型会比较它们的二进制,其结果只有相等或者不想等。而对全文本类型进行等值比较是不太实现…...

汇编——SSE打包整数
SSE也可以进行整数向量的加法,示例如下: ;sse_integer.asm extern printfsection .datadummy db 13 align 16pdivector1 dd 1dd 2dd 3dd 4pdivector2 dd 5dd 6dd 7dd 8fmt1 db "Packed Integer Vector 1: %d, %d, %d, %d",…...

动态规划(2)
动态规划(2) 文章目录 动态规划(2)1、聪明的寻宝人2、基因检测3、药剂稀释4、找相似串 1、聪明的寻宝人 #include <iostream> using namespace std; void MaxValue(int values[], int weights[], int n, int m) {int dp[21…...

JetBrains IDE 2024.1 发布 - 开发者工具
JetBrains IDE 2024.1 (macOS, Linux, Windows) - 开发者工具 CLion, DataGrip, DataSpell, Fleet, GoLand, IntelliJ IDEA, PhpStorm, PyCharm, Rider, RubyMine, WebStorm 请访问原文链接:JetBrains IDE 2024.1 (macOS, Linux, Windows) - 开发者工具࿰…...

C++ 构造函数中的参数顺序
描述: 未初始化的参数必须在初始化参数之前 正确 ✓ 写法: mother(const char* food, const char* lastName"无姓", const char* firstName "无名" ); 错误❌写法: mother(const char* lastName"无姓", …...

Git Flow困境逃脱指南
本来来自极狐GitLab 资源中心,原文链接:https://resources.gitlab.cn/articles/020183ba-cfc0-4917-b901-248acdcfc92f。 GitLab 是一个全球知名的一体化 DevOps 平台,很多人都通过私有化部署 GitLab 来进行源代码托管。极狐GitLab ÿ…...

MySQL的sql_mode模式简介
前言 今天同事使用数据库时报错,排查问题时发现配置文件里的sql_mode配置被人注释了,所以通过查询资料对这个配置进行了下了解。 介绍 mysql为了支持在不同的环境下运行,允许我们给它设置不同的运行模式(sql_mode)。 不同的运行模式&#…...

性能优化-如何爽玩多线程来开发
前言 多线程大家肯定都不陌生,理论滚瓜烂熟,八股天花乱坠,但是大家有多少在代码中实践过呢?很多人在实际开发中可能就用用Async,new Thread()。线程池也很少有人会自己去建,默认的随便用用。在工作中大家对…...
非关系型数据库-----------Redis的主从复制、哨兵模式
目录 一、redis群集有三种模式 1.1主从复制、哨兵、集群的区别 1.1.1主从复制 1.1.2哨兵 1.1.3集群 二、主从复制 2.1主从复制概述 2.2主从复制的作用 ①数据冗余 ②故障恢复 ③负载均衡 ④高可用基石 2.3主从复制流程 2.4搭建redis主从复制 2.4.1环境准备 2.4…...

使用docx4j转换word为pdf处理中文乱码问题
word转pdf 实现方法 mavendocx4j版本自己酌情升级 实现方法 import org.docx4j.Docx4J; import org.docx4j.fonts.IdentityPlusMapper; import org.docx4j.fonts.Mapper; import org.docx4j.fonts.PhysicalFonts; import org.docx4j.openpackaging.packages.WordprocessingMLP…...

【引子】C++从介绍到HelloWorld
C从介绍到HelloWorld 一、C的介绍1. 简介2. 应用场景3. C的标准4. C的运行过程 二、Visual Studio的安装1. 什么是Visual Studio2. Visual Studio的安装 三、完成HelloWorld1.…...
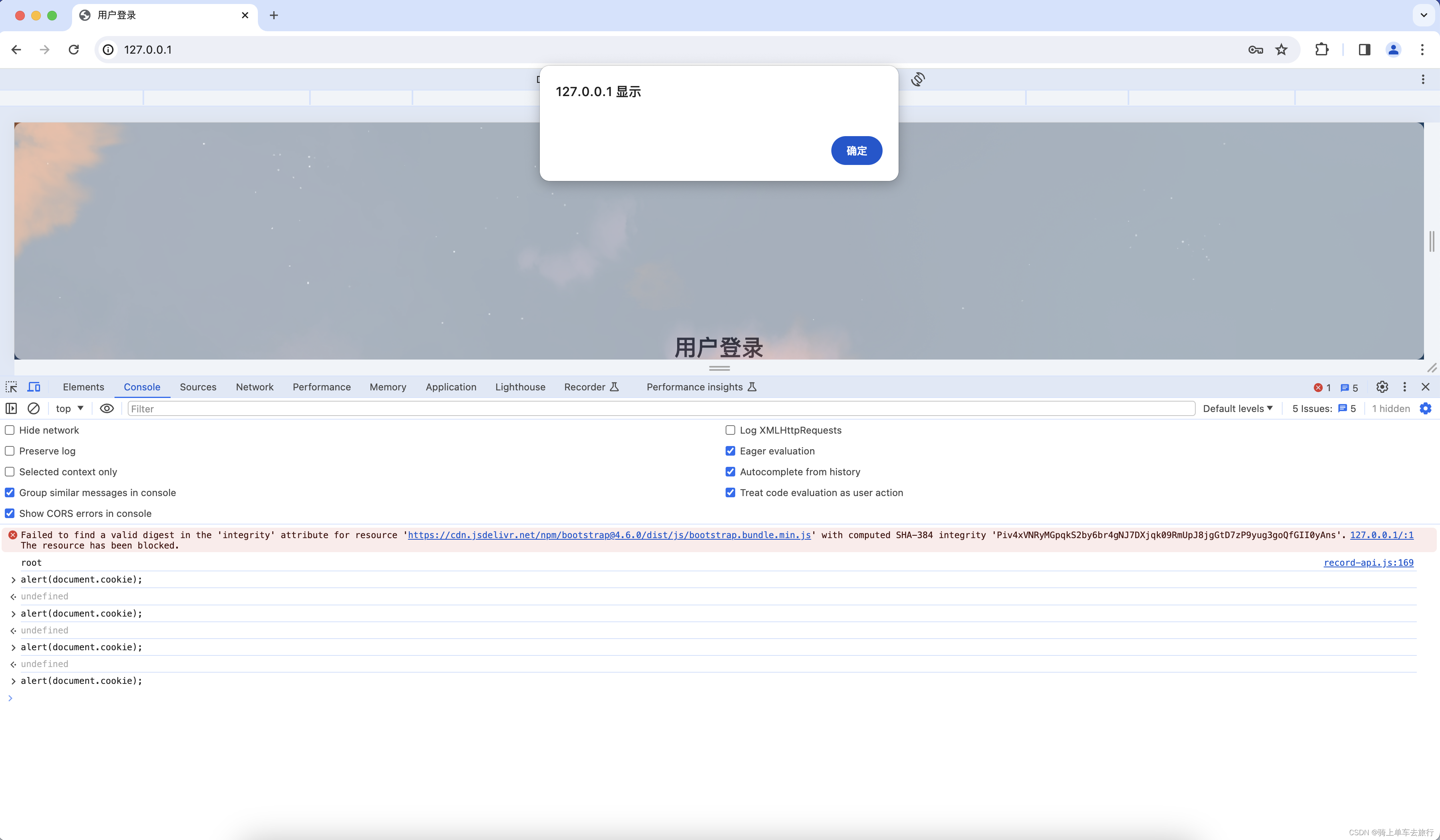
Django检测到会话cookie中缺少HttpOnly属性手工复现
一、漏洞复现 会话cookie中缺少HttpOnly属性会导致攻击者可以通过程序(JS脚本等)获取到用户的cookie信息,造成用户cookie信息泄露,增加攻击者的跨站脚本攻击威胁。 第一步:复制URL:http://192.168.43.219在浏览器打开,…...

2024数字城市建设博览会:一站式平台,满足多元需求
2024数字城市建设博览会:引领未来城市发展的风向标 2024年,一场前所未有的盛会——数字城市建设博览会暨交流大会,将在雄安这座未来之城拉开帷幕。本次大会不仅是数字经济全产业链的精英集结,更是一场汇聚了众多优质项目和丰富客…...
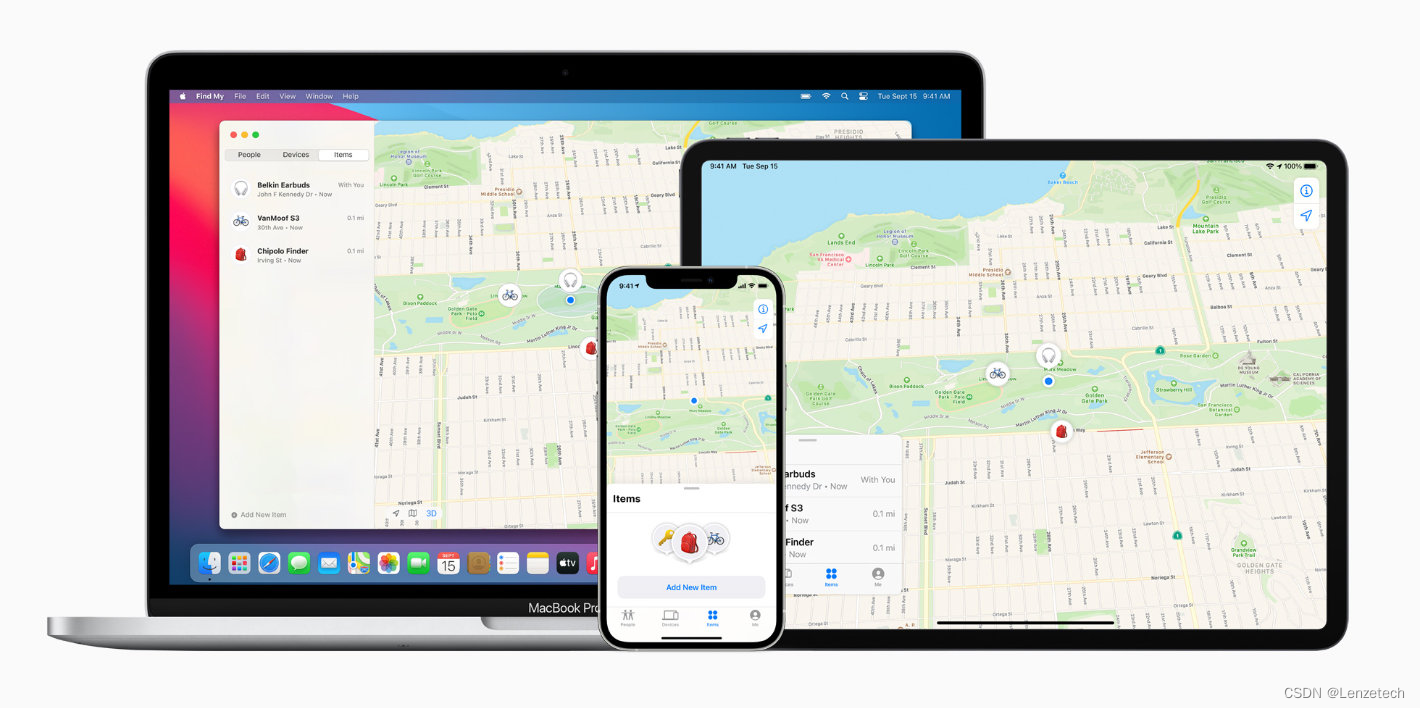
iOS 17.5系统或可识别并禁用未知跟踪器,苹果Find My技术应用越来越合理
苹果公司去年与谷歌合作,宣布将制定新的行业标准来解决人们日益关注的跟踪器隐私问题。苹果计划在即将发布的 iOS 17.5 系统中加入这项提升用户隐私保护的新功能。 科技网站 9to5Mac 在苹果发布的 iOS 17.5 开发者测试版内部代码中发现了这项反跟踪功能的蛛丝马迹…...

关于搭建elk日志平台
我这边是使用docker compose进行的搭建 所以在使用的时候 需要自行提前安装docker以及dockercompose环境 或者从官网下载对应安装包也可以 具体文章看下一章节:【ELK】搭建elk日志平台(使用docker-compose),并接入springboot项目...
网站开发的前置审批是什么意思/域名注册网站哪个好
持久代Permanent Generation space(JDK1.7及以下版本存在)主要存放存放class文件中类的版本、字段、方法、接口,类和方法的元数据等描述信息,运行时常量池,用于存放编译器生成的各种字面量和符号引用。上限是MaxPermSizePremGen与old区绑定在…...

投票网页制作教程/杭州百度seo代理
一、依赖关系 如果想要安装Face_recognitiion,前提是必须要知道以下依赖关系: 情况1:Win下 Anaconda(python3.5以前(含))的版本: 1. 安装face_recongnition的必要条件是:配置好Dlib 2. 配置好dlib的必要条件是:自己安…...

外贸行业有哪些工作岗位/武汉seo管理
二、选择题:本题共8小题,每小题给出的四个选项中,第14~17题只有一项符合题目要求,第18~21题有多项符合题目要求.全部选对的得6分,选对但不全的得3分,有错选或不选的得0分…...

建设的网站别人登录密码/网站自然排名工具
刚刚从博客园看到有朋友用 C# 做了这么个东西, 我用 Delphi 尝试了一下.需要先去申请一个 AppID: http://www.bing.com/toolbox/bingdeveloper/使用帮助在: http://msdn.microsoft.com/en-us/library/dd576287.aspx uses MsXML;{函数} function Translate(AAppID: string; ATex…...

wordpress首页加广告位/关键词排名推广软件
这篇文章主要为大家详细介绍了织梦模板用PHP判断会员是否登录然后返回会员相关信息,具有一定的参考价值,感兴趣的小伙伴们可以参考一下,有需要的朋友可以收藏方便以后借鉴。织梦系统是自带会员系统的,因此我们在网站中很多地方都会自行使用会…...

论坛网站开发平台/百度2022第三季度财报
详见原文博客链接 http://www.killdb.com/2012/08/15/goldengate-%e5%ad%a6%e4%b9%a0%e7%b3%bb%e5%88%971-10gasm-to-11gr2-asm-%e5%8d%95%e5%90%91%e5%a4%8d%e5%88%b6ddl%e6%94%af%e6%8c%81.html...
