LIME: Low-light Image Enhancement viaIllumination Map Estimation
Abstract
当人们在低光条件下拍摄图像时,图像通常会受到低能见度的影响。除了降低图像的视觉美感外,这种不良的质量还可能显著降低许多主要为高质量输入而设计的计算机视觉和多媒体算法的性能。在本文中,我们提出了一种简单而有效的微光图像增强(LIME)方法。更具体地说,首先通过在R、G和B通道中寻找最大值来单独估计每个像素的光照。此外,我们通过在初始光照图之前添加一个结构来细化初始光照图,作为最终的光照图。通过构造良好的光照图,可以实现相应的增强。在一些具有挑战性的弱光图像上进行了实验,以揭示我们的LIME的功效,并显示其在提高质量和效率方面优于几个先进技术。
I. INTRODUCTION
毫无疑问,高可见度的图像反映了目标场景的清晰细节,这对于许多基于视觉的技术来说是至关重要的,如对象检测[1]和跟踪[2]。但是,在弱光条件下拍摄的图像通常能见度很低。首先,在低光条件下拍摄的图像的视觉质量很难令人满意。另一方面,它很可能会损害主要为高可视性输入而设计的算法的性能。图1提供了几个这样的例子,从这些例子中,我们可以看到很多细节,比如第一个例子中墙上的画,第三个例子中左下角远处的田野,最后一个例子中地板上的倒影,几乎都被“掩埋”在黑暗中。为了使被掩埋的信息变得可见,暗光图像增强是必须的。
直接放大暗光图像可能是回忆暗区可见度最直观和最简单的方法。但是,这种操作又产生了另一个问题,即相对明亮的区域可能会饱和,从而丢失相应的细节。直方图均衡化(HE)策略[3],[4],[5]可以通过某种方式迫使输出图像落在[0,1]范围内,从而避免上述问题。此外,变分方法的目标是通过在直方图上施加不同的正则化项来改善HE性能。例如,上下文对比增强(contextual and variational contrast enhancement, CVC)[6]尝试寻找一种关注灰度差异较大的直方图映射,而工作[7]则通过寻求二维直方图(2D histogram, LDR)的分层差分表示来实现改进。然而,在本质上,它们关注的是对比度增强,而不是利用真正的照明原因,存在增强过度或不足的风险。另一种解决方法是伽马校正,这是对图像的非线性操作。主要缺点是Gamma校正的非线性运算是对每个像素单独进行的,没有考虑某个像素与其相邻像素之间的关系,因此可能会使增强结果脆弱,在视觉上与真实场景不一致。
在Retinex理论[8]中,主要的假设是(彩色)图像可以分解为两个因素,即反射率和光照。早期基于Retinex的尝试,如单尺度Retinex (SSR)[9]和多尺度Retinex (MSR)[10],将反射率作为最终的增强结果,往往显得不自然和过度增强。[11]中提出的方法试图在保持光照自然的同时增强对比度。虽然它防止了结果的过度增强,但在我们的实验中,它在效率和视觉质量方面都不如我们的方法令人印象深刻。Fu等人提出了一种通过融合初始估计光照映射(MF)[12]的多个派生来调整光照的方法。MF的表现基本上是有希望的。但是,由于光照结构的盲目性,MF可能会失去纹理丰富区域的真实感。[13]最近的工作提出了一个加权变分模型,用于同时估计反射和光照(SRIE)。利用估计出的反射率和照度,可以通过对照度的控制来增强目标图像。从[14]中可以看出,倒置的弱光图像类似于雾霾图像,如图2所示。基于这一观测结果,[14]的作者对倒置的弱光图像进行了去雾处理。去雾后,将得到的不真实图像再次倒置,作为最终的增强结果。最近,Li等人遵循了这一技术路线,通过先对输入图像进行过分割,然后自适应去噪不同的片段[15],进一步改善了视觉质量。虽然上述类去雾方法可以提供合理的结果,但它们所依赖的基本模型缺乏物理解释。相比之下,我们的方法有明确的物理直觉。
Contribution
我们的方法属于基于Retinex的范畴,它旨在通过估计弱光图像的光照图来增强弱光图像。 值得注意的是,与传统的基于Retinex的方法(如[13]将图像分解为反射率和照度分量)不同,我们的方法只估计一个因子,即照度,从而缩小了解空间,降低了计算代价。 首先通过寻找R、G、B通道中每个像素的最大强度来构造光照图。 然后,利用光照的结构对光照映射进行细化。 提出了一种基于增广拉格朗日乘子(ALM)的算法来精确求解求精问题,并设计了另一种加速求解器来大大减少计算量。 在一些具有挑战性的图像上进行了实验,以揭示我们的方法与其他现有方法相比的优势。
II. METHODOLOGY
我们的方法建立在以下(Retinex)模型之上,该模型解释了微光图像的形成:

其中L和R分别是捕获的图像和期望的恢复。此外,T表示照明图,算子表示逐元素乘法。在本文中,我们假设,对于彩色图像,三个通道共享相同的光照图。我们使用T(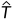 )来交替表示单通道和三通道照明贴图,但稍微滥用了一些符号。模型(1)具有明确的物理意义,即观察到的图像可以分解为期望的光增强场景和照明图的乘积。
)来交替表示单通道和三通道照明贴图,但稍微滥用了一些符号。模型(1)具有明确的物理意义,即观察到的图像可以分解为期望的光增强场景和照明图的乘积。
我们问题的模型与本征图像分解[16]、[17]、[18]、[19]的模型类似,本征图像分解试图将输入分解为两个分量1。然而,本征图像分解的目标是从给定图像中恢复反射分量和阴影分量。如图3(b)所示,反射率失去了盒子的形状(地面真实反射率来自[16]),这不满足弱光图像增强的目的。我们工作的期望是回忆暗区的视觉内容,同时保持视觉真实性,如图3(c)所示。一些研究人员注意到使用反射率作为增强结果的不现实性,例如[9]、[10],并试图通过R f(T)将修改后的照明投影回反射率[13],其中R和T分别是恢复的反射率和照明,f(·)代表操作算子,如Gamma校正。我们可以看到,通过以某种方式再次组合分解的分量来获得期望的增强结果。此外,由于分解问题的不适定性,需要更多的先验知识来帮助约束解的空间。但是如果任务仅仅是使低光图像变亮,这是本文所关注的,则没有必要将输入图像分解成两个分量。因为,通过稍微变换(1),我们得到R = L/T,其中除法是按元素进行的。显然,T的估计是R恢复的关键。这样,问题被简化,仅需要估计T。请注意,L/T可以直接作为光增强结果。
A. Illumination Map Estimation
Max-RGB [8]作为最早的颜色恒常性方法之一,试图通过寻找三个颜色通道(例如R、G和B)的最大值来估计照度。但是这种估计只能提高全局照明。在本文中,为了处理非均匀照明,我们可选地采用以下初始估计:
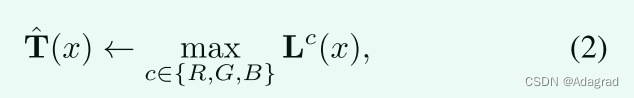
对于每个单独的像素x。上述操作背后的原理是照明至少是在某个位置处的三个通道的最大值。得到的T(x)保证回收率不会饱和,因为
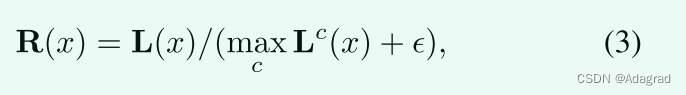
其中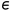 是一个非常小的常数,以避免分母为零。我们指出,这项工作的目的是非均匀地增强低照度图像的照明,而不是消除由光源引起的颜色偏移。
是一个非常小的常数,以避免分母为零。我们指出,这项工作的目的是非均匀地增强低照度图像的照明,而不是消除由光源引起的颜色偏移。
如前所述,另一个广泛使用的模型是基于反转的低光图像1−L看起来类似于薄雾图像的观察,因此表示为[20],[21],[22]:
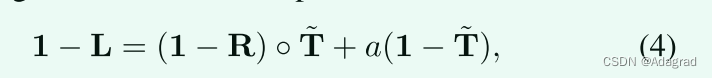
其中A表示全局大气光。虽然倒置的低光图像1 − L的视觉效果直观上类似于霾图像,但与模型(1)相比,上述物理意义仍然模糊。下面我们打算说明(4)和(1)之间的关系。
让我们在这里回忆一下暗通道先验,一种常用的先验估计去雾的透射图[20],在1 − L上如下:
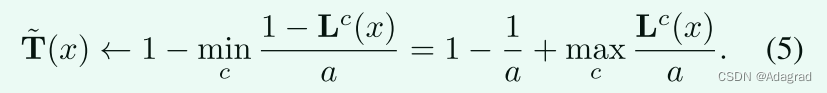
因此,将(5)代入(4)得到:
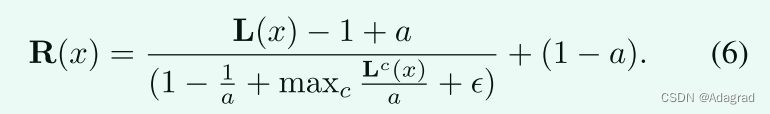
我们可以看到,当a = 1时,(3)和(6)都得到相同的结果。但是,如果a偏离1,模型(6)[14]和(3)之间的等价性就被打破了。从图4可以看出,即使大气光大于0.95,使用(6)和使用(3)之间的视觉差异仍然是显著的。图4(B)中的暗区比图4(c)中的暗区增强程度低,详情请参见放大图。在这项工作中,我们依赖于模型(3)而不涉及大气光a。
在本工作中,我们采用(2)来初始估计照明图T,由于其简单性,尽管在过去几十年中已经开发了各种方法(例如[23]、[24]、[25])来提高精度。这些改进中的大多数本质上通过考虑目标像素周围的小区域内的相邻像素来考虑照明的局部一致性。有代表性的两种方式是:
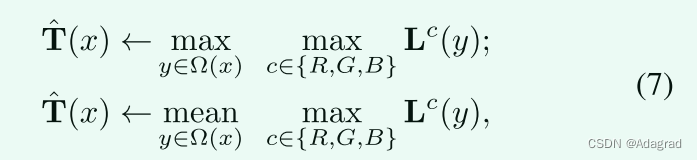
其中Ω(x)是以像素x为中心的区域,y是区域内的位置索引。这些方案虽然能在一定程度上提高算法的局部一致性,但都是结构盲的。在下文中,我们提供了更强大的方案来更好地实现这一目标。
一个"好"的解决方案应该同时保留整体结构和平滑纹理细节。为了解决这个问题,基于初始照明图T,我们提出解决以下优化问题:

其中α是平衡所涉及的两项的系数,k·kF和k·k1分别表示Frobenious和1范数。此外,W是权重矩阵,T是一阶导数滤波器。在本文中,它只包含hT(水平)和vT(垂直)。在目标(8)中,第一项考虑初始映射T和细化映射T之间的保真度,而第二项考虑(结构感知的)平滑度。在讨论构造W的可能策略之前,我们在接下来的两个小节中给出两个求解器来解决问题(8)。
B. Exact Solver to Problem (8)
传统上,问题(8)可以通过交替方向最小化技术有效地解决。从(8)中的目标可以看出,两个项,比如说2和1项,都涉及T。引入辅助变量G代替T,使问题可分,便于求解。因此,T = G被添加为约束。因此,我们有以下等效优化问题:
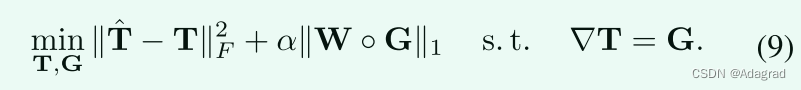
(9)的增广拉格朗日函数可以自然地写成以下形式:
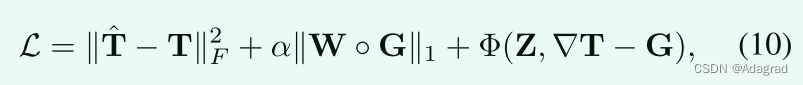
定义为Φ(Z,T − G)= µ 2 k T − Gk2 F + hZ,T − Gi,其中h·,·i表示矩阵内积,µ是正罚标量,Z是拉格朗日乘数。有三个变量,包括T、G和Z需要求解。ALM技术是解决该问题的常见选择(8)。求解器通过固定其他变量,一次迭代更新一个变量,并且每一步都有一个简单的闭合形式解。为了便于分析比较精确解和加速解(后文提出),我们给出了以下子问题的解:
T sub-problem:
从方程中收集T项。(10)给出了如下问题:
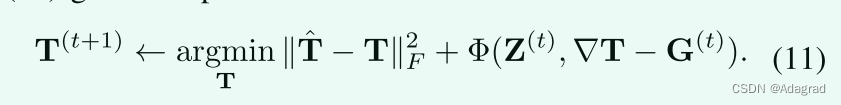
如从公式(11)这是一个经典的最小二乘问题。因此,可以通过关于T求微分(11)并将其设置为0来计算解:
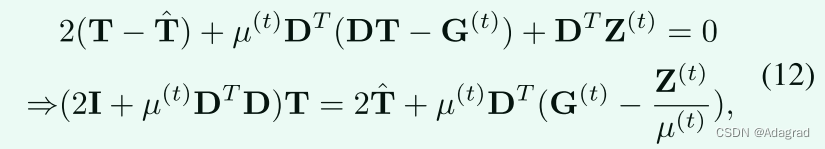
其中I是具有适当大小的单位矩阵。D包含Dh和Dv,它们是由离散梯度算子向前差分得到的Toeplitz矩阵。我们注意到,为了方便起见,操作DX和DTX分别表示整形(Dx)和整形(DTx),其中x是向量化的X,而整形(·)表示将向量整形回其矩阵形式的操作。直接计算2I + µ(t)DTD的倒数是完成这项工作的直观方法。然而,矩阵求逆在计算上是昂贵的,特别是对于像DTD这样的大矩阵。幸运的是,通过假设圆形边界条件,我们可以将二维FFT技术应用于上述问题,这使得我们能够快速计算解。因此,我们有
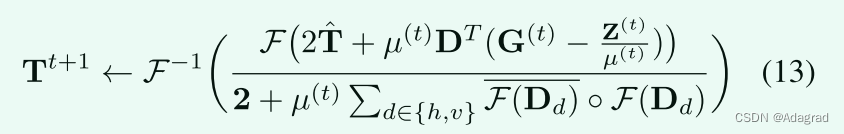
其中F(·)是2D FFT运算符,而F−1(·)和F(·)分别代表2D逆FFT和F(·)的复共轭。除法按元素执行。此外,2是适当大小的矩阵,其所有元素都是2。
G sub-problem:
丢弃与G无关的项导致以下优化问题:
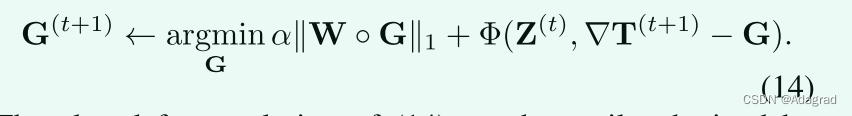
(14)的封闭形式解可以通过执行收缩操作容易地获得,如:
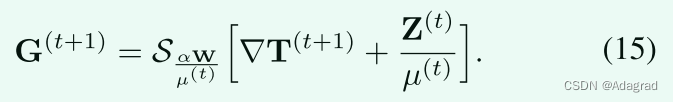
S ε〉0 [·]表示收缩算子,其标量定义为:S ε [x]= sgn(x)最大值(|x|− ε,0)。将收缩算子扩展到向量和矩阵是为了简单地处理数据元素,例如SA [X]利用A的相应条目给出的阈值对X的元素执行收缩。
Z and µ:
Z和µ的更新可通过以下方式完成:
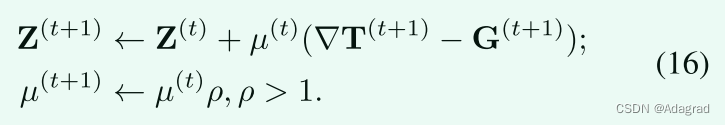
为了清楚起见,在算法1中总结了问题(8)的精确求解器的整个过程。当k T(t +1)− G(t +1)kF ≤ δ k TkF且δ = 10 − 5或达到最大迭代次数时,停止迭代。请参考算法1的其他细节,我们不能涵盖在文本中。
Remark 1 (Convergence and Optimality)
如上所述,问题(9)等价于问题(8)。我们可以观察到,(9)的目标函数中出现的每一项都是凸的,并且约束是仿射的。提出的算法1遵循交替方向最小化增广拉格朗日乘子(ALM-ADM)的框架,其理论保证已经在两块凸情况[26]、[27]中很好地建立。换句话说,我们提出的精确解算器收敛于问题(8)的全局最优解,并且因此收敛于原始(9)。
Remark 2 (Computational Complexity)
算法1的每次迭代涉及三个子问题。关于T子问题,需要O(N logN)来完成计算,其中N是像素的总量。其主要成本来自2D FFT和逆FFT运算。至于G和Z子问题,它们都是关于N的线性问题,即O(N)。因此,每次迭代需要O(N logN)。基于上述,可以得出结论,算法1的复杂度是O(tNlogN),其中t是收敛所需的迭代次数。

C. Sped-up Solver to Problem (8)
虽然算法1是相当低的复杂性,我们想进一步减少。让我们仔细看看问题(8)。原点将迭代过程是稀疏的加权梯度项,即千瓦◦∇Tk1。ℓ1 T标准梯度一起操作有些复杂。显然,适用以下的关系:
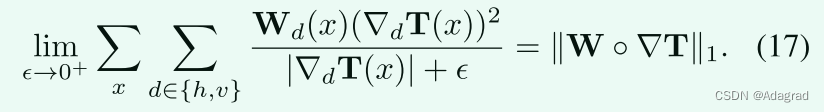
在此基础上,我们用x d ∈ {h,v} Wd(x)(dT(x))2|d|+近似为kW Tk1。结果,(8)的近似问题可以写成如下:
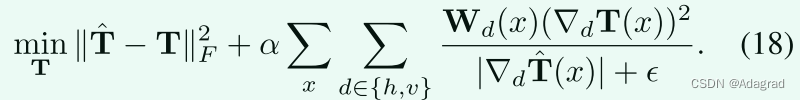
虽然目标函数与原始相比发生了变化,但从初始照明估计值T中提取照明结构的目标与原始一致。更具体地说,当|d|体积小,|dT(x)|即将被抑制,值(dT(x))2也将被抑制|d|+。换句话说,目标T被约束以避免在初始估计的照明图具有小梯度幅度的情况下产生梯度。相反,如果|d|强时,上述抑制减轻,因为该位置更可能在结构边界上而不是在规则纹理上。
如可以观察到的,问题(18)仅涉及二次项。因此,该问题可以通过求解以下方程直接得到:
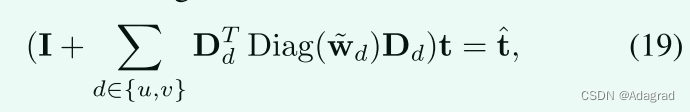
其中w d是W d的向量化版本,W d(x)← Wd(x)|d|+。此外,运算符Diag(x)用于使用向量x构造对角矩阵。由于(I + d ∈ {u,v} DTdDiag(wd)Dd)是一个对称正定的Laplacian矩阵,因此有许多方法可以用来求解它,例如,[28],[29],[30],[31],[32]。
Remark 3 (Computational Complexity)
求解器,如多分辨率预处理共轭梯度可以达到O(N)复杂度。与算法1的复杂度相比,加速求解器消除了迭代要求t,并将N logN减少到N。
D. Possible Weighting Strategies
对于初始光照图的结构感知细化,关键是W的设计。在这一部分,我们讨论了三种可能的加权策略如下。
Strategy I:
可以看出,将权重矩阵设置为
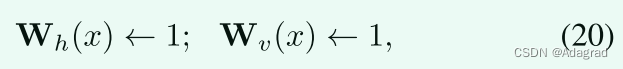
导致经典的2损失总变差最小化问题[33]。
Strategy II:
如第II-C,使用初始照明图的梯度作为权重是合理的。在续集中,我们有:
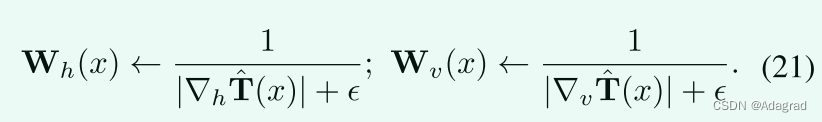
Strategy III:
受相对总变差(RTV)[34]的启发,对于每个位置,通过以下方式设置权重:
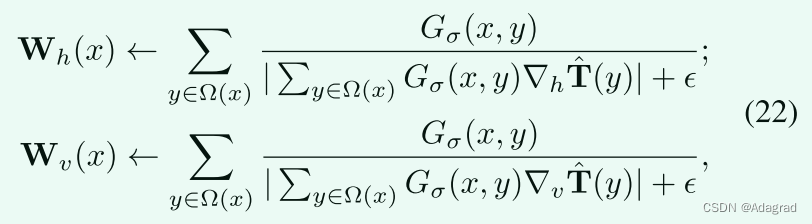
其中Gσ(x,y)由标准差为σ的高斯核产生。形式上,Gσ(x,y)表示为:
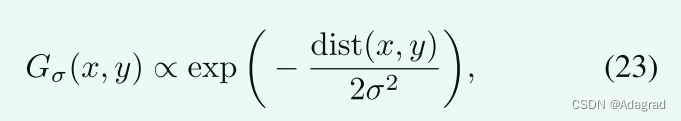
其中函数dist(x,y)用于测量位置x和y之间的空间欧几里得距离。事实上,第二加权策略是这种策略的一个实例。当σ → 0+时,两种策略得到相同的权重矩阵。我们注意到,与RTV不同,我们的权重矩阵是基于给定的T构造的,而不是根据T迭代更新。这意味着W只需要计算一次。

E. Other Operations
有了细化的照明图T,我们可以通过遵循(3)来恢复R。我们也可以通过伽马变换来操纵光照图,比如T ← Tγ。从图7的上一行,我们可以看到将γ设置为0.5、0.8和1时结果之间的差异。对于其余的实验,我们采用γ = 0.8。此外,先前隐藏在黑暗中的可能噪声也相应地被放大,特别是对于非常低的光输入(区域),如图7所示。需要去噪技术来进一步改善视觉质量。许多现成的降噪工具,如[35]、[36]、[37],可以用来完成这项工作。综合性能考虑,BM3D [35]是本工作的选择。在我们的实现中,为了进一步减少计算量,我们只在Y通道上执行BM3D,将R从RGB颜色空间转换为YUV颜色空间。此外,噪声的幅度对于输入的不同区域是不同的,因为放大是不同的。BM3D对不同的面片一视同仁。因此,为了避免处理的不平衡,例如一些(暗)位置被良好地去噪,而一些(亮)位置被过平滑,我们采用以下操作:
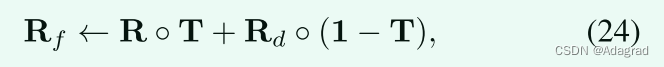
其中Rd和Rf分别是去噪和重组之后的结果。与图7(d)相比,从图7(e)可以看出这种操作的优点。我们想提到的是,去噪加上重组,作为一个后处理步骤,可以连接到任何低光图像增强方法。算法2中概述了LIME的整个过程。
请注意,有时需要其他特定技术来补救低光增强引起的并发症。对于使用JPEG [38]之类的图像压缩,块效应在低光增强结果中变得明显。因此,可能需要解块技术[39]、[40]、[41]、[42]。此外,对于颜色失真的图像,采用一些颜色恒常性方法[43]、[44]作为后处理可以减轻负面影响。在本文中,我们不考虑这些问题(和其他可能的并发症所造成的低光增强),以避免分心。
IV. CONCLUSION
本文提出了一种有效的微光图像增强方法。弱光增强的关键是如何很好地估计照明贴图。为了提高光照一致性,提出了结构感知平滑模型。我们设计了两种算法:一种方法可以获得目标问题的精确最优解,而另一种方法可替换地解决近似问题,显著节省时间。此外,该模型对不同的(结构)加权策略具有通用性.实验结果表明,与现有的几种方法相比,该方法具有一定的优越性。我们的弱光图像增强技术可以为许多基于视觉的应用提供高可见度的输入,从而提高它们的性能,例如边缘检测、特征匹配、目标识别和跟踪。
相关文章:
LIME: Low-light Image Enhancement viaIllumination Map Estimation
Abstract当人们在低光条件下拍摄图像时,图像通常会受到低能见度的影响。除了降低图像的视觉美感外,这种不良的质量还可能显著降低许多主要为高质量输入而设计的计算机视觉和多媒体算法的性能。在本文中,我们提出了一种简单而有效的微光图像增…...

源码指标编写1000问4
4.问: 哪位老师把他改成分析家的,组合公式:猎庄敢死队别样红(凤翔) {猎庄敢死队} rsv:(c-llv(l,9))/(hhv(h,9)-llv(l,9))100; stickline(1,50,50,1,0),pointdot,Linethick2,colorff00; k:sma(rsv,3,1); d:sma(k,3,1); rsv1:(hhv(h,9.8)-c)/(hhv(h,9.8)-llv(l,9.8))1…...

Golang中GC和三色屏障机制【Golang面试必考】
文章目录Go v1.3 标记—清楚(mark and sweep)方法Go V1.5 三色标记法三色标记过程无STW的问题强弱三色不变式插入写屏障Go V1.8的三色标记法混合写屏障机制混合写屏障场景场景1:对象被一个堆对象删除引用,成为栈对象的下游场景2:对象被一个栈对象删除引用࿰…...
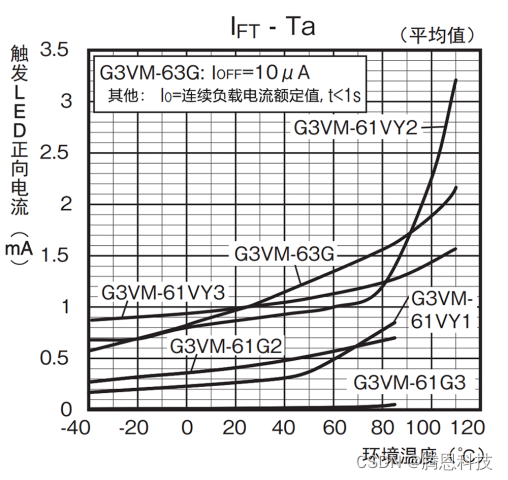
MOS FET继电器(无机械触点继电器)设计输入侧电源时的电流值概念
设计输入侧电源时的问题 机械式继电器、MOS FET继电器分别具有不同的特长。基于对MOS FET继电器所具小型及长寿命、静音动作等优势的需求,目前已经出现了所用机械式继电器向MOS FET继电器转化的趋势。 但是,由于机械式继电器与MOS FET继电器在产品结构…...

5. 驱动开发
文章目录一、驱动开发1.1 前言1.2 何谓驱动框架1.3 内核驱动框架中LED的基本情况1.3.1 相关文件1.3.2 九鼎移植的内核中led驱动1.3.3 案例分析驱动框架的使用1.3.4 典型的驱动开发行业现状1.4 初步分析led驱动框架源码1.4.1 涉及到的文件1.4.2 subsys_initcall1.4.3 led_class_…...

模板方法模式详解
模板方法模式(行为模式) 1. 模板方法模式介绍 父类定义算法骨架,细节的具体实现延迟到子类子类只是定义某些自己的个性化处理,但不改变执行顺序 2. 好处 减少代码冗余,共性抽取后算法流程更加清晰与规范降低流程性…...

关于 Lightweight process container,ChatGPT的答案
晓楚 Can you give me a list of process container? As an AI language model, I can provide you with a list of popular process containers, which are as follows: Docker Kubernetes Apache Mesos LXC OpenVZ systemd-nspawn rkt (Rocket) Linux Containers (LXC) Ga…...

机器学习和深度学习的综述
机器学习和深度学习的综述 1.1.1人工智能、机器学习、深度学习的关系 人工智能(Artificial Intelligence,AI)是最宽泛的概念,是研发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。由于这个定义…...

Synopsys Sentaurus TCAD系列教程之--Sprocess(SmallMOS_2D3D) 解析
SmallMOS_2D3D解析 #header## STI depth set sti_depth 0.15 ## Half STI width set sti_width sti_width ## Half gate length set gate_len <lg/2> ## SD length (from center) set sd_len [expr $gate_len0.05]#endheader## X lines line x location 0.0 spacing 0.…...
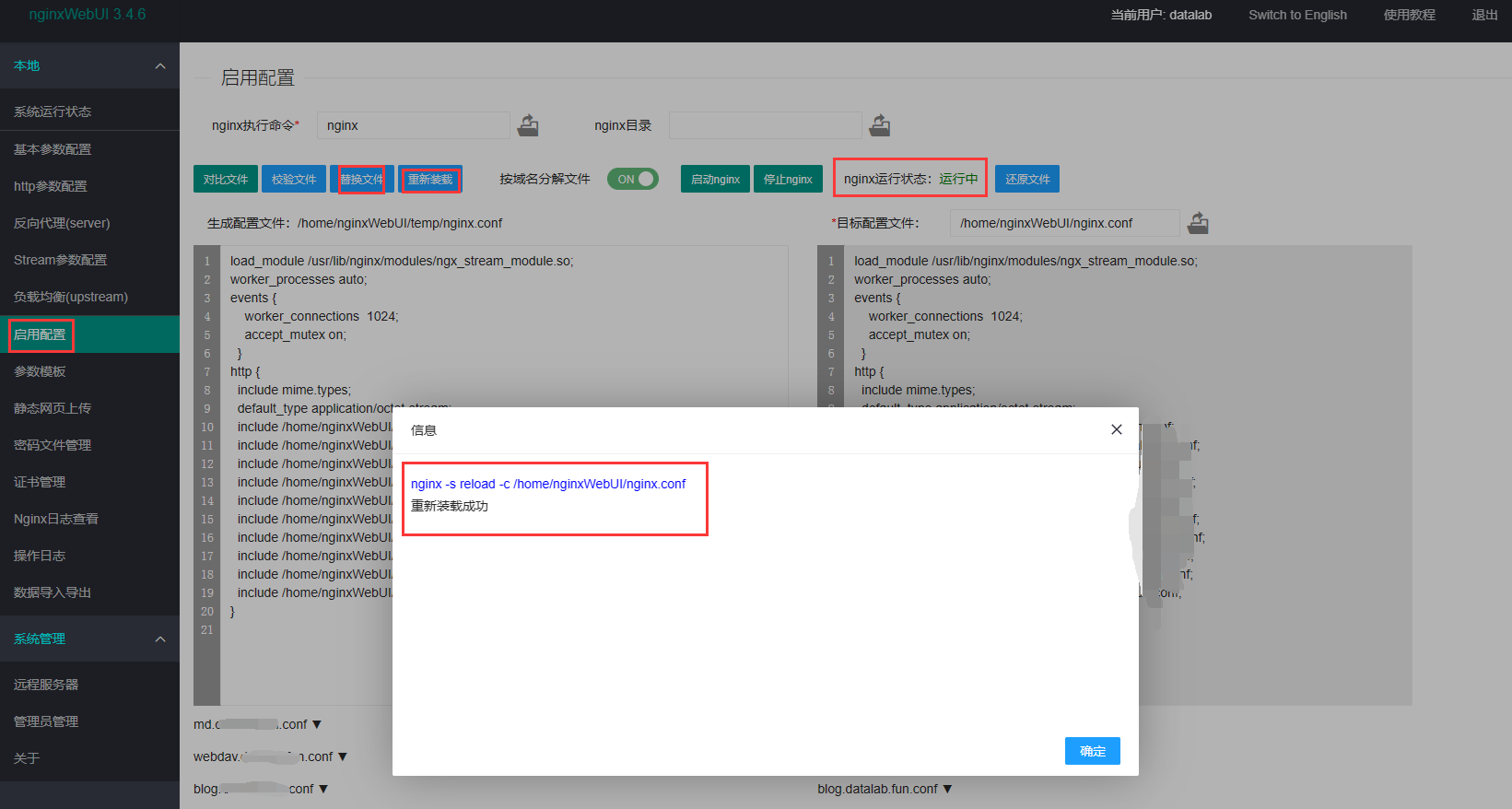
好使!NAS中傻瓜式配置反向代理及SSL证书,提升网络安全性!
对于有NAS或者有个人主机的朋友来说,将机器映射到外网是基本操作。 但是一般来说,能直接从外网访问的往往仅有80和443端口。事实上,运营商一般把家庭宽带的这两个端口都封了,所以如果我们想要从外网访问自己家中机器部署的服务&a…...

数据结构队列-先进先出
一,概述 队列这个概念非常好理解。你可以把它想象成排队买票,先来的先买,后来的人只能站末尾,不允许插队。先进者先出,这就是典型的“队列”。 二,顺序队列和链式队列 队列和栈一样,也是一种…...

CentOS 7使用TiUP部署TiDB
本文主要是根据官方文档指导,结合实际主机情况,在Cent OS7上使用TiUP在线部署TiDB。 环境说明 类型操作系统版本配置中控机Deepin 20.34核CPU6G内存40G硬盘TiDB部署机Cent OS 7.38核CPU48G内存100硬盘网络情况中控机与外网相连,中控机与部署…...
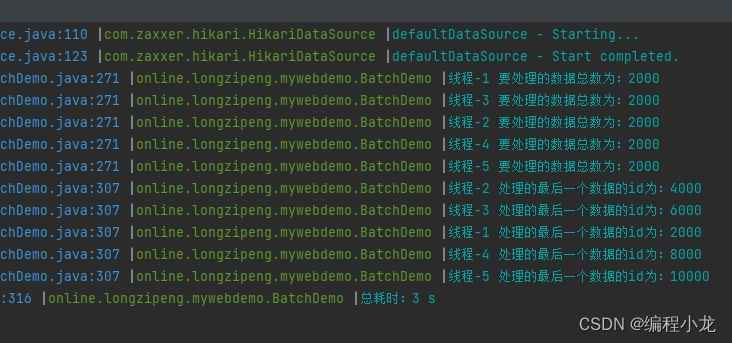
java单元测试批处理数据模板【亿点点日志配合分页以及多线程处理】
文章目录引入相关资料环境准备分页查询处理,减少单次批量处理的数据量级补充亿点点日志,更易观察多线程优化查询_切数据版多线程_每个线程都分页处理引入 都说后端开发能顶半个运维,我们经常需要对大量输出进行需求调整,很多时候…...
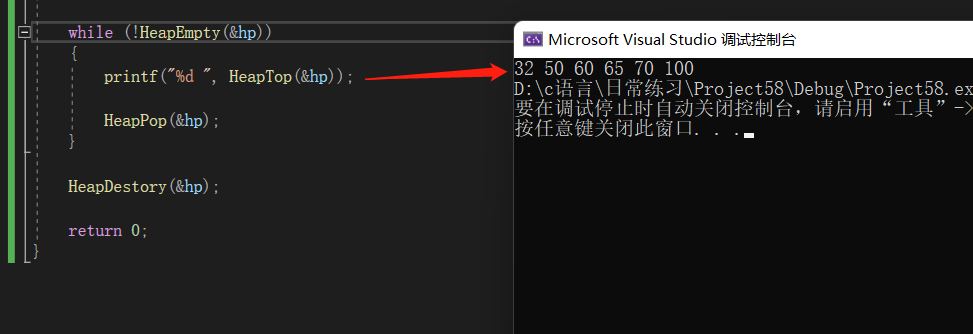
【数据结构】模拟实现 堆
堆数据结构是一种数组对象,它可以被看作一颗完全二叉树的结构(数组是完全二叉树),堆是一种静态结构。堆分为最大堆和最小堆。最大堆:每个父结点都大于孩子结点。最小堆:每个父结点都小于孩子结点。堆的优势…...
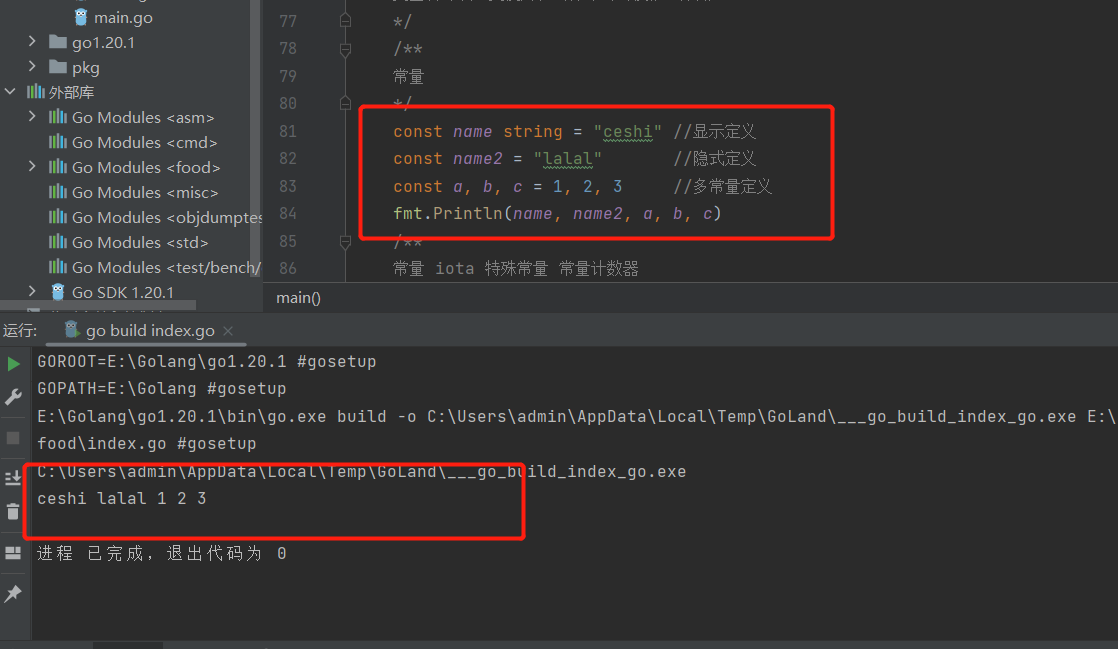
Go语言学习的第三天--上部分(基础用法)
前两天经过不断度娘,与对up主的跟踪学习了解了go的历史,今天开始了go的基础!!本章主要是go 的注释、变量及常量的梳理一、注释不管什么语言都有自己的注释,go也不例外 !!单行注释 // 多行注释 …...
linux面试基础篇
题目目录1.简述DNS分离解析的工作原理,关键配置2.apache有几种工作模式,分别简述两种工作模式及其优缺点?3.写出172.0.0.38/27 的网络id与广播地址4.写出下列服务使用的传输层协议(TCP/UDP)及默认端口5.在局域网想获得…...
黑马程序员提高变成
这里写目录标题函数模板1.2.2 函数模板注意事项1.2.3 函数模板案例调用规则类模板与函数模板区别类模板与继承类模板成员函数类外实现#pragma once类模板与友元案例重新定义【】stl2.2 STL基本概念STL六大组件容器算法迭代器初识vectorvector容器嵌套容器string容器string赋值操…...

MySQL5种索引类型
MySQL的类型主要有五种:主键索引、唯一索引、普通索引、空间索引、全文索引 有表: CREATE TABLE t1 ( id bigint unsigned NOT NULL AUTO_INCREMENT, u1 int unsigned NOT NULL DEFAULT 0, u2 int unsigned NOT NULL DEFAULT 0, u3 varchar(20) NOT NU…...

uniapp封装缓存方法,支持类似cookie具有过期时间
1、定义CacheManage类,有set和get方法 class CacheManage {set() {},get() {} }set用来设置缓存,get用来获取缓存 2、完善set业务逻辑 大概逻辑如下: 1、将接收params参数,包含key、data、unit、time key 缓存字段,…...
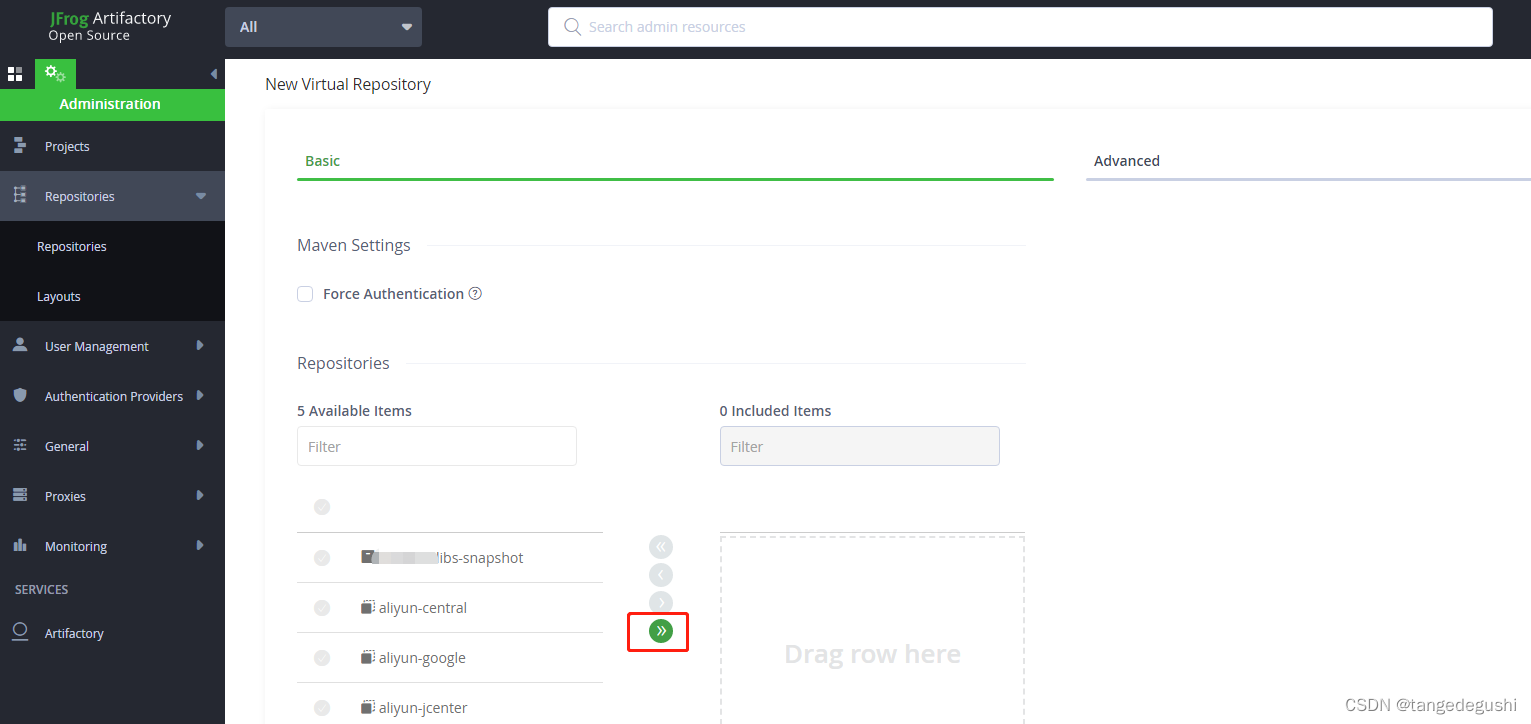
Jfrog 搭建本地maven仓库以及上传Android库
Jfrog 下载 安装包下载地址:Download Artifactory OSS | JFrog 如果是想下载之前的版本,可以点击上面的Get code source ,如果是最新版本,直接点下面的下载就好。下面以Linux安装为例。 Jfrog安装 对于Linux而言,其实…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
