Python|蓝桥杯进阶第二卷——贪心

欢迎交流学习~~
专栏: 蓝桥杯Python组刷题日寄
蓝桥杯进阶系列:
🏆 Python | 蓝桥杯进阶第一卷——字符串
🔎 Python | 蓝桥杯进阶第二卷——贪心
💝 Python | 蓝桥杯进阶第三卷——动态规划(待续)
✈️ Python | 蓝桥杯进阶第四卷——图论(待续)
🌞 Python | 蓝桥杯进阶第五卷——数论(待续)
🌠 Python | 蓝桥杯进阶第六卷——递归(待续)
💎 Python | 蓝桥杯进阶第七卷——搜索(待续)
Python|蓝桥杯进阶第二卷——贪心
- 🎁 发工资喽
- 🌲 翻硬币
- 🚀 Huffuman树
- 💡 打水问题
- 🍞 排队打水问题
🎁 发工资喽
题目:
时间限制:
1s
内存限制:
128MB
题目描述:
作为程序猿,最盼望的日子就是每月的9号了,因为这一天是发工资的日子,养家糊口就靠它了,呵呵
但是对于公司财务处的工作人员来说,这一天则是很忙碌的一天,财务处的小李最近就在考虑一个问题:如果每个员工的工资额都知道,最少需要准备多少张人民币,才能在给每位员工发工资的时候都不用员工找零呢?
这里假设程序猿的工资都是正整数,单位元,人民币一共有 100 元、50 元、10 元、5 元、2 元和 1 元六种。
输入描述:
输入数据包含多个测试实例,每个测试实例的第一行是一个整数n(n<100),表示员工的人数,然后是 n 个员工的工资。
n=0 表示输入的结束,不做处理。
输出描述:
对于每个测试实例输出一个整数 x,表示至少需要准备的人民币张数。每个输出占一行。
样例输入:
3 1 2 3
0
样例输出:
4
解题思路
贪心,从面值最大的开始选取,直到满足条件。
参考代码
def func(amount):count1, temp = divmod(amount, 100)count2, temp = divmod(temp, 50)count3, temp = divmod(temp, 10)count4, temp = divmod(temp, 5)count5, temp = divmod(temp, 2)total = count1 + count2 + count3 + count4 + count5 + tempreturn totalwhile True:try:nums = list(map(int, input().split()))n = nums[0]if n != 0:count = 0for i in range(n):count += func(nums[i+1])print(count)except:break
🌲 翻硬币
题目:
时间限制:
1s
内存限制:
128MB
题目描述:
小明正在玩一个“翻硬币”的游戏。
桌上放着排成一排的若干硬币。我们用 * 表示正面,用 o 表示反面(是小写字母,不是零)。
比如,可能情形是:**oo***oooo
如果同时翻转左边的两个硬币,则变为:oooo***oooo
现在小明的问题是:如果已知了初始状态和要达到的目标状态,每次只能同时翻转相邻的两个硬币,那么对特定的局面,最少要翻动多少次呢?
我们约定:把翻动相邻的两个硬币叫做一步操作。
输入描述:
两行等长的字符串,分别表示初始状态和要达到的目标状态。每行的长度 <1000
输出描述:
一个整数,表示最小操作步数。
样例输入:
*o**o***o***
*o***o**o***
样例输出:
1
解题思路
从左到右遍历,如果对应位置两状态不同,就进行翻转,计数。
参考代码
start = list(input())
end = list(input())
L = len(start)
count = 0for i in range(L):if start[i] != end[i]:start[i] = 'o' if start[i] == '*' else '*'start[i+1] = 'o' if start[i+1] == '*' else '*'count += 1print(count)
🚀 Huffuman树
题目:
时间限制:
3s
内存限制:
192MB
题目描述:
Huffman树在编码中有着广泛的应用。在这里,我们只关心Huffman树的构造过程。
给出一列数 {pi}={p0, p1, …, pn-1},用这列数构造Huffman树的过程如下:
-
找到
{pi}中最小的两个数,设为pa和pb,将pa和pb从{pi}中删除掉,然后将它们的和加入到{pi}中。这个过程的费用记为pa + pb。 -
重复步骤1,直到
{pi}中只剩下一个数。
在上面的操作过程中,把所有的费用相加,就得到了构造Huffman树的总费用。
本题任务:对于给定的一个数列,现在请你求出用该数列构造Huffman树的总费用。
例如,对于数列 {pi}={5, 3, 8, 2, 9},Huffman树的构造过程如下:
-
找到
{5, 3, 8, 2, 9}中最小的两个数,分别是2和3,从{pi}中删除它们并将和5加入,得到{5, 8, 9, 5},费用为5。 -
找到
{5, 8, 9, 5}中最小的两个数,分别是5和5,从{pi}中删除它们并将和10加入,得到{8, 9, 10},费用为10。 -
找到
{8, 9, 10}中最小的两个数,分别是8和9,从{pi}中删除它们并将和17加入,得到{10, 17},费用为17。 -
找到
{10, 17}中最小的两个数,分别是10和17,从{pi}中删除它们并将和27加入,得到{27},费用为27。 -
现在,数列中只剩下一个数
27,构造过程结束,总费用为5+10+17+27=59。
输入描述:
输入的第一行包含一个正整数 n(n< =100)。
接下来是 n 个正整数,表示 p0, p1, …, pn-1,每个数不超过 1000。
输出描述:
输出用这些数构造Huffman树的总费用。
样例输入:
5
5 3 8 2 9
样例输出:
59
解题思路
排序后循环 n-1 次,每次选出前两个(最小值),计算其和后,再加入列表中,并将这两个最小值删除。
参考代码
n = int(input())
nums = list(map(int, input().split()))
res = 0
nums.sort()for i in range(n-1):total = nums[0] + nums[1]nums.append(total)res += totalnums.pop(0)nums.pop(0)nums.sort()
print(res)
💡 打水问题
题目:
时间限制:
1s
内存限制:
128MB
题目描述:
N 个人要打水,有 M 个水龙头,第 i 个人打水所需时间为 Ti,请安排一个合理的方案使得所有人的等待时间之和尽量小。
提示:
一种最佳打水方案是,将 N 个人按照 Ti 从小到大的顺序依次分配到 M 个龙头打水。
例如样例中,Ti 从小到大排序为 1,2,3,4,5,6,7,将他们依次分配到 3 个龙头,则去龙头一打水的为1,4,7;去龙头二打水的为2, 5;去第三个龙头打水的为 3, 6。
第一个龙头打水的人总等待时间 = 0 + 1 + (1 + 4) = 6
第二个龙头打水的人总等待时间 = 0 + 2 = 2
第三个龙头打水的人总等待时间 = 0 + 3 = 3
所以总的等待时间 = 6 + 2 + 3 = 11
输入描述:
第一行两个正整数 N M 接下来一行 N 个正整数 Ti。
N,M< =1000,Ti< =1000
输出描述:
最小的等待时间之和。(不需要输出具体的安排方案)
样例输入:
7 3
3 6 1 4 2 5 7
样例输出:
11
解题思路
排序后直接计算。
参考代码
n, m = map(int, input().split())
t = list(map(int, input().split()))
t.sort()
res = 0
# 只有 n-m 个要等待
for i in range(0, n-m):t[i+m] += t[i]res += t[i]
print(res)
🍞 排队打水问题
题目:
时间限制:
1s
内存限制:
128MB
题目描述:
有 n 个人排队到 r 个水龙头去打水,他们装满水桶的时间 t1、t2………..tn 为整数且各不相等,应如何安排他们的打水顺序才能使他们总共花费的时间最少?
输入描述:
第一行 n,r (n< =500,r< =75)
第二行为 n 个人打水所用的时间 Ti (Ti< =100);
数据规模和约定
其中 80% 的数据保证 n< =10
输出描述:
最少的花费时间
样例输入:
3 2
1 2 3
样例输出:
7
解题思路
假设多了 m 个打水时间为 0 的人,此时需要可以转化为前一个问题,此时有 n 个需要等待的人。
参考代码
n, m = map(int, input().split())
t = list(map(int, input().split()))
t.sort()
res = 0
# 要计算总花费时间,我们可以假设多了 m 个打水时间为0的人
t += [0 for i in range(m)]
# 即计算n个等待的人
for i in range(0, n):t[i+m] += t[i]res += t[i]
print(res)
相关文章:

Python|蓝桥杯进阶第二卷——贪心
欢迎交流学习~~ 专栏: 蓝桥杯Python组刷题日寄 蓝桥杯进阶系列: 🏆 Python | 蓝桥杯进阶第一卷——字符串 🔎 Python | 蓝桥杯进阶第二卷——贪心 💝 Python | 蓝桥杯进阶第三卷——动态规划(待续…...

Chrome开发使用技巧总结
Chrome一个程序员开发神器,但是好多猿子们不会或者没有正确使用。今天教大家如何利用它快速高效的开发调试工作。代码格式化有很多css/js的代码都会被 minify 掉,你可以点击代码窗口左下角的那个 { } 标签,chrome会帮你给格式化掉。强制DOM状…...

你真的会在阳光下拍照片么?
你好,我是小麥。 上节课我们讲了如何通过影子判断光的质量,也就是光的软硬,这节课我们来接着说一说光的方向和环境光的实际运用。 虽然在现实生活里,我们可能没有从软硬的角度观察过光线,但我相信你在拍照片的时候一…...
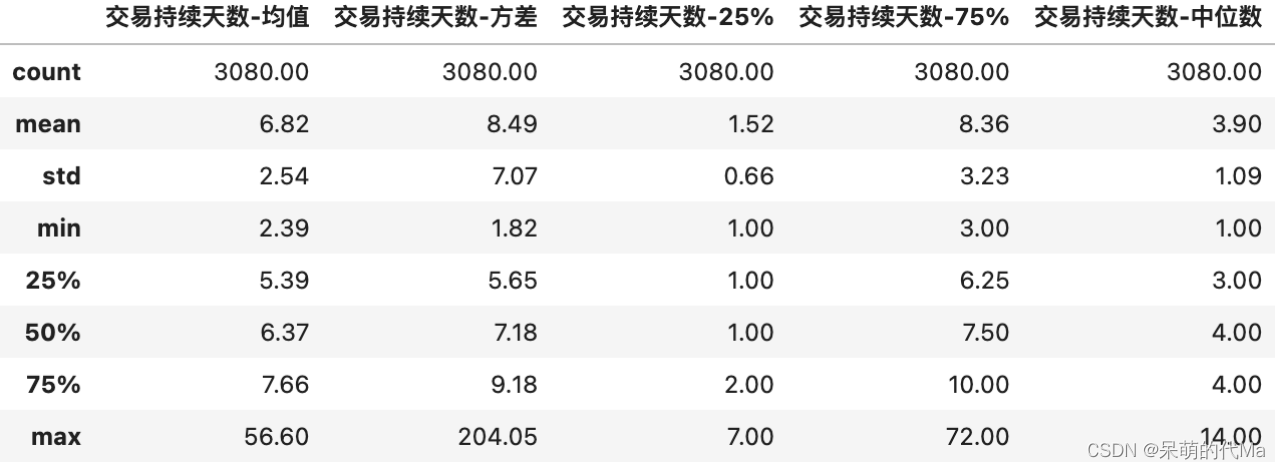
量化择时——均线策略及改进方法(第1部分—因子测算)
文章目录道氏理论个股股价走势阶段板块、行业股价走势均线策略交易逻辑均线策略效果测算改进一:设置策略信号偏移量改进二:生成止盈止损信号道氏理论 使用盘面数据,根据计算出的一条或多条均线,判断入场与离场的时机,…...

封装几个有用的 Vue3 组合式API
本文将介绍如何使用Vue3来封装一些比较有用的组合API,主要包括背景、实现思路以及一些思考。 就我自己的感觉而言,Hook与Composition API概念是很类似的,事实上在React大部分可用的Hook都可以使用Vue3再实现一遍。 为了拼写方便,下文内容均使用Hook代替Composition API。相…...
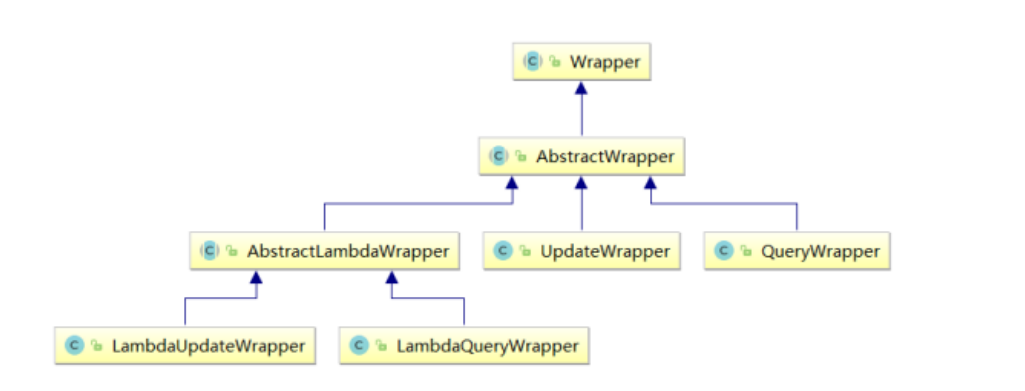
MyBatisPlus中的条件构造器Wrapper
引言为什么要了解Wrapper?Wrapper解决的了什么问题?一、Wrapper:条件构造抽象类,用来解决单表操作出现的一些复杂问题,例如排序,和模糊查询等等结构图文字解释AbstractWrapper : 用于查询条件封装ÿ…...

类和对象及其构造方法
类和对象 现实世界的事物由什么组成? 属性 行为 类也可以包含属性和行为,所以使用类描述现实世界事物是非常合适的类和对象的关系是什么? 类是程序中的“设计图纸” 对象是基于图纸生产的具体实体什么是面向对象编程? 面向对象编…...

HStream Console、HStreamDB 0.14 发布
近两个月,HStreamDB 相继发布了 0.13 和 0.14 版本,包含多项已知问题修复。同时,我们也发布了全新的 HStream Console 组件,为 HStreamDB 带来了简洁友好的图形化管理界面,将帮助用户更轻松地使用和管理 HStreamDB. H…...

参考文献怎么查找,去哪里查找?一篇文章讲明白这些问题
在我们撰写论文查找参考文献时,往往不知道从哪里入手,本文小编就针对下面这三个方面给大家详细讲解下: 一、查找参考文献方法 二、参考文献资料查找网站 三、参考文献格式规范 一、查找参考文献方法: 1、知网全球最大的中文数据…...
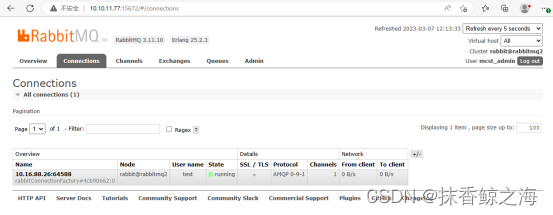
docker-compose+HAProxy+Keepalived搭建高可用 RabbitMQ 集群
基础环境准备 系统环境:Centos7.6 Docker version: 1.13.1, build 7d71120/1.13.1 Docker Compose version: v2.2.2 三个节点: 10.10.11.79 (这一台做rabbitmq集群根节点) 10.10.11.80 (这台做haproxyke…...

自动化框架如何搭建?让10年阿里自动化测试老司机帮你搞定!自动化测试脚本怎么写?
一、何为框架?何为自动化测试框架? 无论是日常技术交流,还是在自动化测试实践中,经常会听到一个词叫:框架。之前对“框架”这个词知其然不知其所以然。现在看过一些资料以及加上我自己的一些实践有了我自己的一些看法…...

剑指 Offer 15. 二进制中1的个数
剑指 Offer 15. 二进制中1的个数 难度:easy\color{Green}{easy}easy 题目描述 编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为 汉明重量).…...
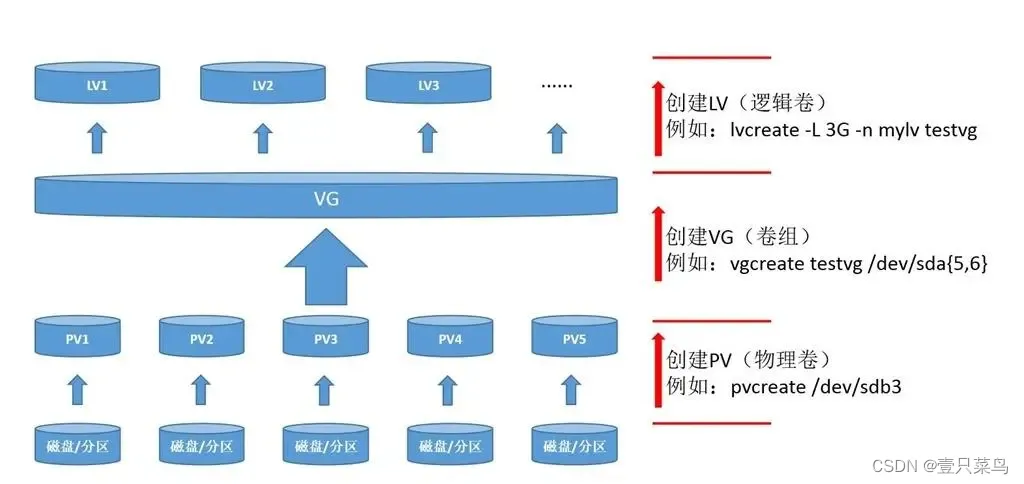
CHAPTER 3 磁盘管理
磁盘管理1 磁盘管理1.1 块设备信息(lsblk)1.2 挂载硬盘1.2.1 挂载单个硬盘(mkfs、mount)1.2.2 磁盘分区工具(fdisk)1.2.3 创建分区1.2.4 相关命令1. df2. partprobe3. mkfs1.3 逻辑卷管理器(LVM)1. 涉及概念2. 使用LVM流程1.4 磁盘检测及修复(fsck)1 磁盘…...
MS python学习(7)
Managing Keys - dotenv Managing keys usage of .env module 项目地址:https://github.com/theskumar/python-dotenv Reads the key,value pair from .env and adds them to environment variable. 将key明文(hard code)形式写在script里…...
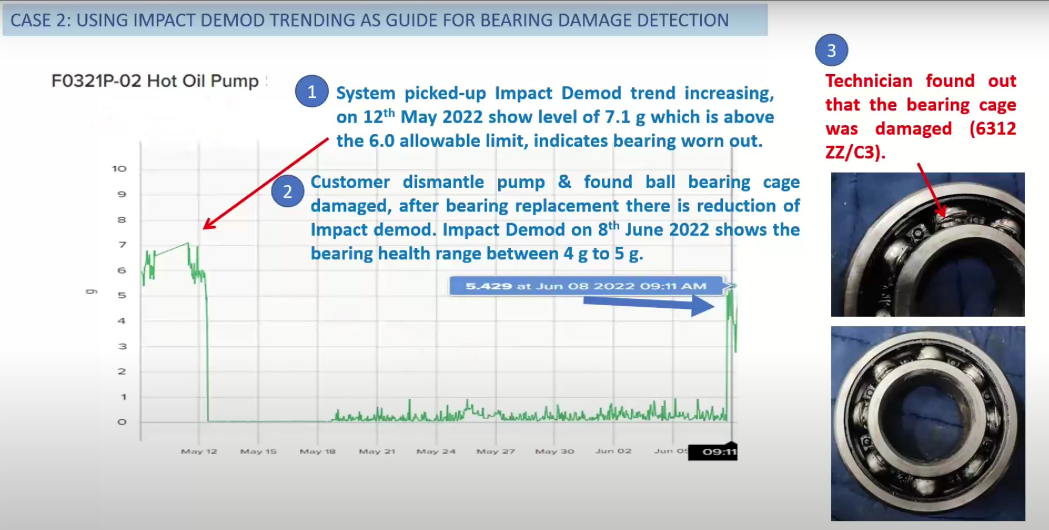
工业物联网“杀手级”应用—预测性维护
一、预测性维护的必要性 随着新一轮科技革命和产业变革的兴起,工业物联网、大数据、人工智能等技术正与经济社会各领域加速渗透融合。由于市场竞争对精细化成本管控的要求,设备的重要性越来越凸显,设备的维护对策也必然从响应式维护…...
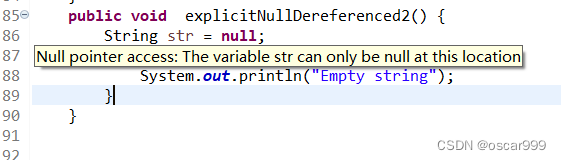
Java代码弱点与修复之——Explicit null dereferenced(显式空间接引用)
弱点描述 Explicit null dereferenced, 显示空间接引用。是 Coverity 静态代码分析工具检测到的一种中风险缺陷。这种缺陷通常发生在尝试使用空指针引用调用对象上的方法或访问属性时。 Explicit null dereferenced的缺陷可能会导致程序崩溃或产生不可预测的结果。 在Java语…...

一元导数与多元求导数总结
前序:文章结构 1.一元导数 ①一般函数求导 因为太简单的原因,事实上一般函数求导不会单独出现,大多数都是出现在各种特殊的求导过程中。只要掌握16个基本求导公式没问题。 ②复合函数求导(主要链式法则) 这种一般是…...

通过堆栈分析深拷贝、浅拷贝、赋值的差异
前言数据类型分为:基本数据类型String、Number、Boolean、Null、Undefined、Symbol对象数据类型Object、Array基本数据类型的特点:直接存储在栈(stack)中的数据引用数据类型的特点:存储的是该对象在栈中引用,真实的数据存放在堆内…...

网络割接概述
网络割接概述割接背景企业网络的变化割接概述割接难点割接的操作流程情景模拟及解决方案常见的割接场景割接背景 随着企业业务的不断发展,企业网络为了适应业务的需求不断的改造和优化。无论是硬件的扩容、软件的升级、配置的变更,凡是影响现网运行业务…...
)
开放开源开先河(下)
目录 1.唯一性定义品牌 2.打造爆款塑造品牌 3.生态系统传播品牌 打造爆款塑造品牌 目前全球100多个开源基金会大部分都在美国,已成功孵化了800多个项目。而开放原子开源基金会现有136家捐赠单位,2020年9月,百度将区块链项目超级链࿰…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
