算法设计与分析实验报告c++实现(最近点对问题、循环赛日程安排问题、排序问题、棋盘覆盖问题)
一、实验目的
1.加深学生对分治法算法设计方法的基本思想、基本步骤、基本方法的理解与掌握;
2.提高学生利用课堂所学知识解决实际问题的能力;
3.提高学生综合应用所学知识解决实际问题的能力。
二、实验任务
1、最近对问题
设p1=(x1, y1), p2=(x2, y2), …, pn=(xn, yn)是平面上n个点构成的集合S,设计算法找出集合S中距离最近的点对。
(1)分别用蛮力法和分治法求解最近对问题;
(2)分析算法的时间性能,设计实验程序验证分析结论。
2、循环赛日程安排问题
设有n=2k个选手要进行网球循环赛,要求设计一个满足以下要求的比赛日程表:
(1)每个选手必须与其他n-1个选手各赛一次;
(2)每个选手一天只能赛一次。
3、排序问题
目前已知有几十种排序算法,请查找资料,并尽可能多地实现多种排序算法,并分析算法的时间复杂度。比较各种算法的优劣(冒泡排序、选择排序、插入排序、二分插入排序、希尔排序、归并排序、堆排序、快速排序等,需比较分析各种算法的时间复杂度及排序的稳定性)
4、用分治策略,设计解棋盘覆盖问题的一个简洁算法
三、实验设备及编程开发工具
编程开发工具:Microsoft Visual c++
四、实验过程设计(算法设计过程)
(一)最近对问题
1、基本算法思想
蛮力法:在蛮力法实现最近点对问题中,将问题简化:距离最近的点对可能多于一对,找出一对即可,另外只考虑二维平面中的情况。此处考虑到直接用公式计算其距离(欧几里得距离)。通过遍历所有点集,计算出每一个点对的距离,计算出最近的距离并输出。避免同一对点计算两次,只考虑i<j的点对(pi,pj)。
分治法:在利用分治法思想解决此问题时,首先考虑将最近对问题进行分治,设计其分治策略。将集合S分成两个子集S1和S2,根据平衡子问题原则,每个子集中的点数大致都为n/2。这样分治后,最近点对将会出现三种情况:在S1中,在S2中或者最近点对分别在集合S1和S2中。利用递归分析法分别计算前两种情况,第三种方法另外分析。求解出三类子情况后,再合并三类情况,比较分析后输出三者中最小的距离。
2、源程序
#include<iostream>
#include<stdio.h>
#include<stdio.h>
#include<algorithm>
#include<math.h>
#include<windows.h>
using namespace std;struct point {double x;double y;
}P[100];
double distance(point p1, point p2) {return sqrt((p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y));
}
bool cmp1(point p1, point p2) {return p1.x < p2.x;
}
bool cmp2(point p1, point p2) {return p1.y < p2.y;
}
//蛮力法
double get_min(int n)
{double min = sqrt((P[0].x - P[1].x)*(P[0].x - P[1].x) + (P[0].y - P[1].y)*(P[0].y - P[1].y));//设置第一个计算值最短距离for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {double t = sqrt((P[i].x - P[j].x)*(P[i].x - P[j].x) + (P[i].y - P[j].y)*(P[i].y - P[j].y));if (min>t)min = t;}//循环比较计算值}return min;
}
//分治法
double nearest_pair(point S[],int left,int right) {cout << left << " " << right << endl;if (right-left == 1) {return distance(S[right], S[left]);}if (right - left == 2) {double d1 = distance(S[right], S[left]);double d2 = distance(S[right], S[right + 1]);double d3 = distance(S[right + 1], S[left]);d2 = min(d1, d2);d3 = min(d2, d3);return d3;}int m = (right+left) / 2;double d1 = nearest_pair(S,left, m);double d2 = nearest_pair(S, m+1,right);//sort(S+right, S+left, cmp2);double d = min(d1, d2);int l = left, r = right;while (S[l].x < S[m].x - d && l <= right);l++;while (S[r].x > S[m].x + d && r>=left)r++;sort(S + 1, S + r + 1, cmp2);double d3;for (int i = l; i <= r; i++) {for (int j = i + 1; j <= r; j++) {if (S[j].y - S[i].y >= d) {break;}else {d3 = distance(S[i], S[j]);if (d3 < d)d = d3;}}}return d;
}
int main()
{int n;cout << "Input n:";//设置平面中点的个数cin >> n;for (int i = 1; i <= n; i++) {cout << "Input the " << i << "th number:";cin >> P[i].x >> P[i].y;}//逐个设置第i个点的坐标sort(P + 1, P + n+1, cmp1);for ( i = 1; i <= n; i++) {cout << P[i].x << " " << P[i].y << endl;}double m = get_min(n);cout <<"蛮力法结果:"<< m << endl;//蛮力法输出结果double m2 = nearest_pair(P, 1, n);cout <<"分治法结果:" <<m2 << endl;//分治法输出结果system("pause");return 0;
}(二)循环赛日程安排问题
1、基本算法思想
假设n位选手被顺序编号为1,2,…,n,比赛的日程表是一个n行n-1列的表格,i行j列的表格内容是第i号选手在第j天的比赛对手。
根据分而治之的原则,可从其中一半选手(2^(n-1位)的比赛日程,导出全体n位选手的日程,最终细分到只有两位选手的比赛日程出发。
2、源程序
#include<stdio.h>
#include<math.h>
#define N 50
void GameTable(int k,int array[][N]);
void print(int k,int array[][N]); //输出二维数组
main()
{int k;int array[N][N];printf("参赛选手的人数为n(n=2^k),请输入k 的值:");do{scanf("%d",&k);if(k>0){GameTable(k,array);print(k,array);}elseprintf("您输入的数据有误,请重新输入"); }while(k!=0);//排除输入错误k值}
void GameTable(int k,int array[][N])//数组下标从1开始
{int i,j,s,t;int n=1;for(i=1;i<=k;i++)n*=2; //求总人数for(i=1;i<=n;i++)array[1][i]=i; //第一行排1-8int m=1; //用来控制每一次填表时i行j列的起始填充位置for(s=1;s<=k;s++) //s指对称赋值的总循环次数,即分成几大步进行制作日程表{n=n/2;for(t=1;t<=n;t++) //t指明内部对称赋值的循环次数for(i=m+1;i<=2*m;i++)for(j=m+1;j<=2*m;j++){array[i][j+(t-1)*m*2]=array[i-m][j+(t-1)*m*2-m]; //右上角等于左上角的值array[i][j+(t-1)*m*2-m]=array[i-m][j+(t-1)*m*2]; //左下角等于右上角的值}m*=2;}}
void print(int k,int array[][N])
{int i,j;int num=pow(2,k);printf("%d人的循环赛日程表如下:\n",num);for(i=1;i<=num;i++) //输出二维数组 {for(j=1;j<=num;j++){printf("%d\t",array[i][j]);}printf("\n");}
}(三)排序问题
(1)直接插入排序
将一个记录插入到已排序好的有序表中,从而得到一个新,记录数增1的有序表。即:先将序列的第1个记录看成是一个有序的子序列,然后从第2个记录逐个进行插入,直至整个序列有序为止。
void InsertSort(int a[], int n)
{for(int i= 1; i<n; i++){if(a[i] < a[i-1]){//若第i个元素大于i-1元素,直接插入。小于的话,移动有序表后插入int j= i-1; int x = a[i]; //复制为哨兵,即存储待排序元素a[i] = a[i-1]; //先后移一个元素while(x < a[j]){ //查找在有序表的插入位置a[j+1] = a[j];j--; //元素后移}a[j+1] = x; //插入到正确位置}print(a,n,i); //打印每趟排序的结果 }
}
(2)希尔排序
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。
void ShellInsertSort(int a[], int n, int dk)
{for(int i= dk; i<n; ++i){if(a[i] < a[i-dk]){ //若第i个元素大于i-1元素,直接插入。小于的话,移动有序表后插入int j = i-dk; int x = a[i]; //复制为哨兵,即存储待排序元素a[i] = a[i-dk]; //首先后移一个元素while(x < a[j]){ //查找在有序表的插入位置a[j+dk] = a[j];j -= dk; //元素后移}a[j+dk] = x; //插入到正确位置}print(a, n,i );}}/*** 先按增量d(n/2,n为要排序数的个数进行希尔排序**/
void shellSort(int a[], int n){int dk = n/2;while( dk >= 1 ){ShellInsertSort(a, n, dk);dk = dk/2;}
}(3)简单选择排序
int SelectMinKey(int a[], int n, int i)
{int k = i;for(int j=i+1 ;j< n; ++j) {if(a[k] > a[j]) k = j;}return k;
}/*** 选择排序**/
void selectSort(int a[], int n){int key, tmp;for(int i = 0; i< n; ++i) {key = SelectMinKey(a, n,i); //选择最小的元素if(key != i){tmp = a[i]; a[i] = a[key]; a[key] = tmp; //最小元素与第i位置元素互换}print(a, n , i);}
}(4)冒泡排序
两两比较相邻记录的关键字,如果反序则交换,直到没有反序的记录为止。
void BubbleSort(int *p, int length)
{for (int i = 0; i < length-1; i++){for (int j =length-1; j>=i;j--){if (p[j-1] > p[j]){swap(p[j-1], p[j]);}}}
}(5)堆排序
堆排序的基本思想(利用堆,如大顶堆进行排序):将待排序的序列构造成一个大顶堆。此时,整个序列的最大值就是堆顶的根结点。将它移走(其实就是将它与堆数组的末尾元素交换,此时末尾元素就是最大值),然后将剩余n-1个序列重新构造成一个堆,这样就会得到n个元素的次小值。如此反复执行,便能得到一个有序序列。
//构造最大堆void MaxHeapFixDown(int *p, int i, int length) {int j = 2 * i + 1;int temp = p[i];while (j<length) {if (j + 1<length && p[j]<p[j + 1])++j;if (temp>p[j])break;else {p[i] = p[j];i = j;j = 2 * i + 1;}}p[i] = temp;
}
//堆排序void HeapSort(int *p, int length) {for (int i = length / 2 - 1; i >= 0; i--){MaxHeapFixDown(p, i, length);}for (int i = length - 1; i >= 1; i--){swap(p[i], p[0]);MaxHeapFixDown(p, 0, i);cout << "i的值:" << i << " 排序:";ergodic(p, 9);}
}(6)归并排序
归并排序就是利用归并思想实现的排序方法。原理:假设初始序列含有n个记录,则可以看成是n个有序的子序列,每个子序列长度为1,然后再两两归并,得到[n/2]个长度为2或1的有序子序列;再两两归并….,如此重复,直到的一个长度为n的有序序列为止,称为2路归并排序。
//将r[i…m]和r[m +1 …n]归并到辅助数组rf[i…n]
void Merge(ElemType *r,ElemType *rf, int i, int m, int n)
{int j,k;for(j=m+1,k=i; i<=m && j <=n ; ++k){if(r[j] < r[i]) rf[k] = r[j++];else rf[k] = r[i++];}while(i <= m) rf[k++] = r[i++];while(j <= n) rf[k++] = r[j++];
}void MergeSort(ElemType *r, ElemType *rf, int lenght)
{ int len = 1;ElemType *q = r ;ElemType *tmp ;while(len < lenght) {int s = len;len = 2 * s ;int i = 0;while(i+ len <lenght){Merge(q, rf, i, i+ s-1, i+ len-1 ); //对等长的两个子表合并i = i+ len;}if(i + s < lenght){Merge(q, rf, i, i+ s -1, lenght -1); //对不等长的两个子表合并}tmp = q; q = rf; rf = tmp; //交换q,rf,以保证下一趟归并时,仍从q 归并到rf}
}(7)快速排序
1)选择一个基准元素,通常选择第一个元素或者最后一个元素,
2)通过一趟排序讲待排序的记录分割成独立的两部分,其中一部分记录的元素值均比基准元素值小。另一部分记录的 元素值比基准值大。
3)此时基准元素在其排好序后的正确位置
4)然后分别对这两部分记录用同样的方法继续进行排序,直到整个序列有序
void swap(int *a, int *b)
{int tmp = *a;*a = *b;*b = tmp;
}
int partition(int a[], int low, int high)
{int privotKey = a[low]; //基准元素while(low < high){ //从表的两端交替地向中间扫描while(low < high && a[high] >= privotKey) --high; //从high 所指位置向前搜索,至多到low+1 位置。将比基准元素小的交换到低端swap(&a[low], &a[high]);while(low < high && a[low] <= privotKey ) ++low;swap(&a[low], &a[high]);}print(a,10);return low;
}
void quickSort(int a[], int low, int high){if(low < high){int privotLoc = partition(a, low, high); //将表一分为二quickSort(a, low, privotLoc -1); //递归对低子表递归排序quickSort(a, privotLoc + 1, high); //递归对高子表递归排序}
}(四)棋盘覆盖问题
1、基本算法原理
当k>0时,将2k×2k棋盘分割为4个2k-1×2k-1 子棋盘(a)所示。特殊方格必位于4个较小子棋盘之一中,其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘,可以用一个L型骨牌覆盖这3个较小棋盘的会合处,从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割,直至棋盘简化为棋盘1×1
2、源代码
//棋盘覆盖问题
/*
(tr,tc)是棋盘左上角的方格坐标
(dr,dc)是特殊方格所在的坐标
size是棋盘的行数和列数
*/
#include<iostream>
using namespace std;
int board[1025][1025];
static int tile = 1;
void ChessBoard(int tr,int tc,int dr,int dc,int size)
{if(size==1) return ;//递归边界int t=tile++;//L型骨牌号int s=size/2;//分割棋盘//覆盖左上角子棋盘if(dr<tr+s && dc<tc+s)ChessBoard(tr,tc,dr,dc,s);//特殊方格在此棋盘中else //此棋盘中无特殊方格,用t号L型骨牌覆盖右下角{board[tr+s-1][tc+s-1]=t;//覆盖其余方格ChessBoard(tr,tc,tr+s-1,tc+s-1,s);}//覆盖右上角子棋盘if(dr<tr+s && dc>=tc+s)ChessBoard(tr,tc+s,dr,dc,s);//特殊方格在此棋盘中else //此棋盘中无特殊方格,用t号L型骨牌覆盖左下角{board[tr+s-1][tc+s]=t;//覆盖其余方格ChessBoard(tr,tc+s,tr+s-1,tc+s,s);}//覆盖左下角子棋盘if(dr>=tr+s && dc<tc+s)//特殊方格在此棋盘中ChessBoard(tr+s,tc,dr,dc,s);else //此棋盘中无特殊方格,用t号L型骨牌覆盖右上角{board[tr+s][tc+s-1]=t;//覆盖其余方格ChessBoard(tr+s,tc,tr+s,tc+s-1,s);}//覆盖右下角子棋盘if(dr>=tr+s && dc>=tc+s)//特殊方格在此棋盘中ChessBoard(tr+s,tc+s,dr,dc,s);else //此棋盘中无特殊方格,用t号L型骨牌覆盖左上角{board[tr+s][tc+s]=t;//覆盖其余方格ChessBoard(tr+s,tc+s,tr+s,tc+s,s);}
}
int main()
{int i,j;int k;//棋盘大小为2^kcout<<"棋盘大小为2^k,请输入k的值:";while(cin>>k){int size = 1<<k;int x,y;//x,y为特殊方格的坐标cout<<"请输入特殊方格的坐标:";cin>>x>>y;board[x][y]=0;ChessBoard(0, 0, x, y, size);for(i=0; i<size; i++){for(j = 0; j < size; j++)cout<< board[i][j]<<"\t";cout<<"\n";}}
return 0;
}五、实验结果及算法复杂度分析
(一)最近对问题
1、实验结果
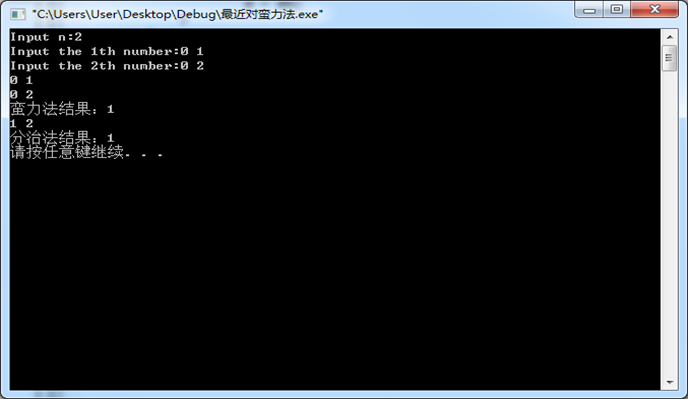
2、时间复杂度
蛮力法:O(n^2)
分治法:O(nlog2n)
(二)循环赛日程安排问题
1、实验结果
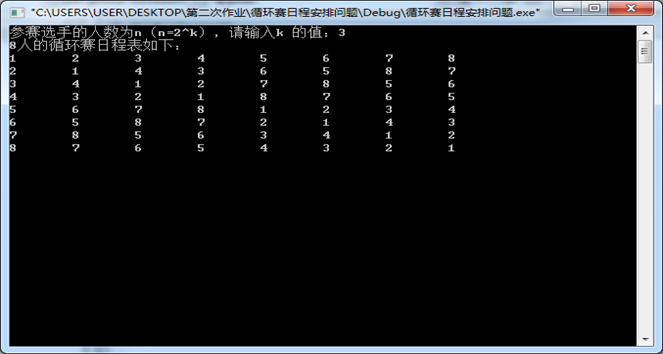
2、时间复杂度
时间复杂度:O(2^k * 2^k)
(三)排序问题
1、实验结果
1、直接插入排序
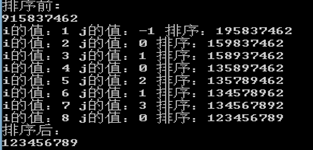
2、 希尔排序
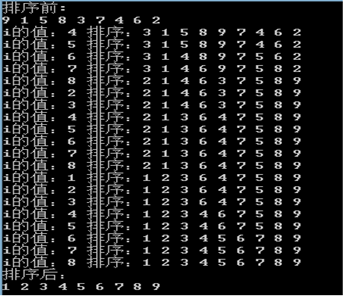
3、简单选择排序
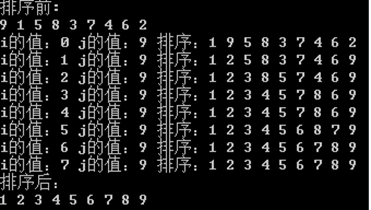
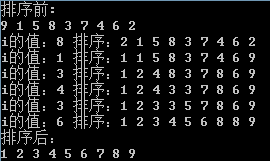
4、冒泡排序
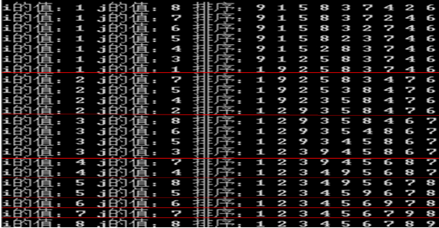
5、 堆排序
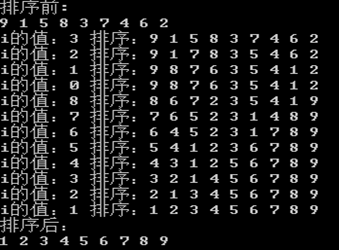
7、快速排
2、时间复杂度
1、直接插入排序时间复杂度:O(n^2);
2、 希尔排序时间复杂度:O(n^2);
3、简单选择排序时间复杂度:O(n^2);
4、冒泡排序时间复杂度:O(n^2);
5、 堆排序时间复杂度:O(nlog2n);
6、 归并排序时间复杂度:O(nlog n);
7、快速排序时间复杂度:0(n^2)。
(四)棋盘覆盖问题
1、实验结果
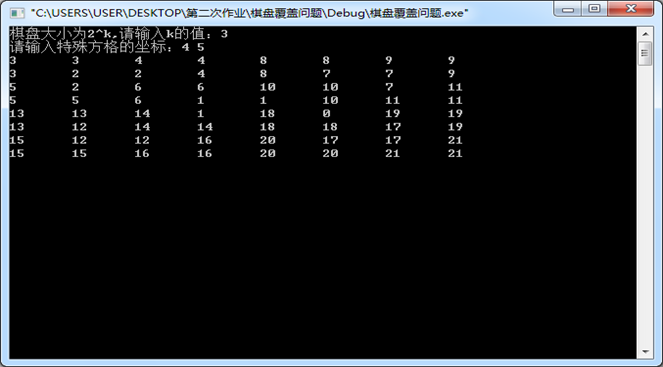
2、时间复杂度
最坏时间复杂度:O(4^k)
实验小结(包括问题和解决方法、心得体会等)
本次实验的中心思想就是分治法,在课堂教学中老师就对分治法进行了比较深刻的讲解,再加上在网上百度就对分治法有了比较清楚的认识,字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。在通过实验的四道题目的实践,相信自己对分治法已经足够掌握了。
相关文章:

算法设计与分析实验报告c++实现(最近点对问题、循环赛日程安排问题、排序问题、棋盘覆盖问题)
一、实验目的 1.加深学生对分治法算法设计方法的基本思想、基本步骤、基本方法的理解与掌握; 2.提高学生利用课堂所学知识解决实际问题的能力; 3.提高学生综合应用所学知识解决实际问题的能力。 二、实验任务 1、最…...

Vue - 你知道Vue中computed和watch的区别吗
难度级别:中高级及以上 提问概率:70% 二者都是用来监听数据变化的,而且在日常工作中大部分时候都只是局限于简单实用,所以到了面试中很难全面说出二者的区别。接下来我们看一下,二者究竟有哪些区别呢? 先说computed,它的主要用途是监听…...
POJ2976 Dropping tests——P4377 [USACO18OPEN] Talent Show G 【分数规划二分法+贪心/背包】
POJ2976 Dropping tests 【分数规划二分法+贪心】 有 n 个物品,每个物品有两个权值 a 和b。你可以放弃 k 个物品,选 n-k 个物品,使得最大。 输入多个样例,第一行输入n 和 k,第二行输入n 个 ai ,第三行输入 n 个 bi,输入 0 0 结束。 输出答案乘100 后四舍五入到整数…...
【生产实习-毕设】pyspark学生成绩分析与预测(上)
注意:数据由实习单位老师提供(需要自行搜索下载),页面美化为下载模板。 项目介绍:前端页面输入影响成绩的属性,预测出成绩,并作可视化展示——属性对成绩的影响。使用python pyspark 进行数据预…...

【华为笔试题汇总】2024-04-10-华为春招笔试题(第二套)-三语言题解(CPP/Python/Java)
🍭 大家好这里是KK爱Coding ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为近期的春秋招笔试题汇总~ 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢…...
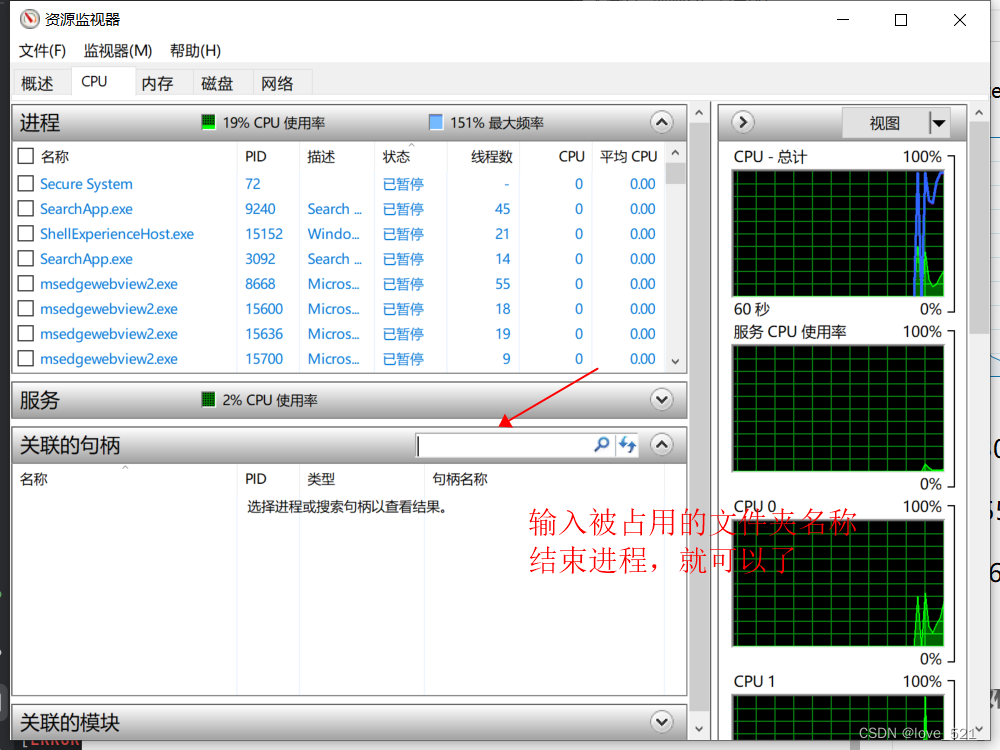
Windows 文件夹被占用无法删除
按下键盘上的“Ctrl Alt Delete”键打开任务管理器...

PHP+MySQL组合开发 易企秀H5场景源码系统 带完整的安装代码包以及搭建教程
在数字化时代,企业对于宣传与推广的需求日益增长,而H5页面作为一种轻量级、跨平台的宣传方式,深受企业青睐。为了满足企业对于H5页面制作的需求,我们基于PHPMySQL组合开发了一套易企秀H5场景源码系统,并提供了完整的安…...
抖音小店入驻有什么条件?资金少,没经验的普通人做得起吗?
大家好,我是电商花花。 在直播电商的推动下,抖音小店独特的电商模式下吸引着众多的商家,吸引着一波又一波的创业者入驻,想要在抖音小店上开垦出属于自己的电商净土。 想要入驻抖音小店还需要一些条件,然后才能入驻成…...
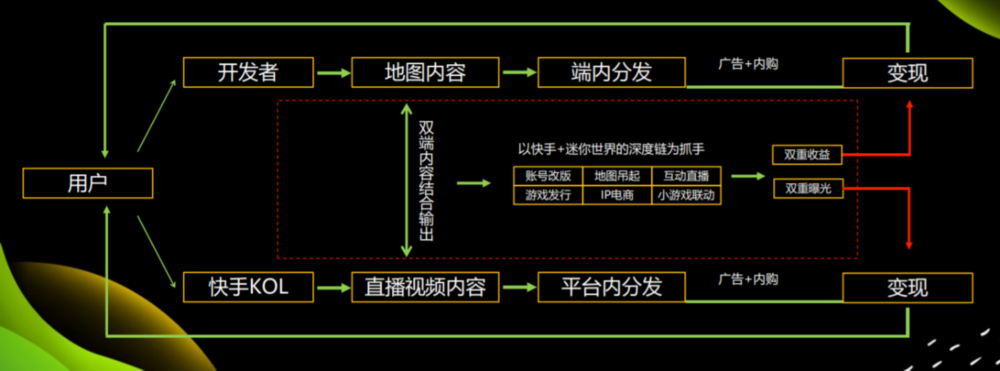
游戏行业科普 (二)游戏是怎么做出来,怎么卖出去的?
游戏行业科普系列文章,大家可以关注起来,等我慢慢芬分享~~ 《蛋仔派对》 一、研运流程--游戏是怎么做出来的 一款游戏的开发和运营大体上可以分为预研立项、设计开发、测试调优、发行上线和成熟运营几个阶段。 1)预研立项: 初始研…...

Java研学-RBAC权限控制(二)
三 PageHelper 1 分页所需 // 原分页所需 1. 定义QueryObject类,传递分页参数,currentPage,pageSize,get start();方法 2. selectForCount()方法,总条数小于等于0说明不需要分页,大于0说明可以分页 3. se…...

20. 【Android教程】拖动条 SeekBar
这一节要学的控件是 ProgressBar 的升级版,对于 ProgressBar 而言只能展示进度,而不能与用户互动,也就是没有接收用户输入的能力。而本节要学习的 SeekBar 是一种可以“Seek”的 ProgressBar,用户不但可以通过 SeekBar 观察到进度…...

工业物联网网关在机械设备制造企业数转过程的应用-天拓四方
随着科技的飞速发展,物联网技术已经渗透到工业领域的每一个角落。作为连接物理世界和数字世界的桥梁,工业物联网网关在推动企业数字化转型中发挥着至关重要的作用。数字化转型已经成为企业提升竞争力的必由之路,然而,在转型过程中…...
《一》Qt的概述
1.1 什么是Qt Qt是一个跨平台的C图形用户界面应用程序框架。它为应用程序开发者提供建立图形界面所需的所有功能。它是完全面向对象的,很容易扩展,并且允许真正的组件编程。 1.2 Qt的发展史 1991年 Qt最早由芬兰奇趣科技开发 1996年 进入商业领域&#x…...

局域网共享文件夹怎么加密?局域网共享文件夹加密方法介绍
在企业局域网中,共享文件夹扮演着重要的角色。为了保护数据安全,我们需要加密保护局域网共享文件夹。那么,局域网共享文件夹怎么加密?下面我们来了解一下吧。 局域网共享文件夹加密方法 局域网共享文件夹加密推荐使用共享文件夹加…...

计算机网络——网络地址转换(NAT)技术
目录 前言 前篇 引言 SNAT(Source Network Address Translation)源网络地址转换 SNAT流程 确定性标记 DNAT(Destination Network Address Translation,目标网络地址转换) NAT技术重要性 前言 本博客是博主用于…...

【感谢】心怀感恩,共赴知识之旅——致每一位陪伴我突破百万总访问量的您
小伙伴朋友们: 此刻,我怀着无比激动与深深感激的心情,写下这篇特别的博文。今天,我的CSDN总访问量成功突破了百万大关,这不仅是一个数字的跨越,更是你们对我的支持、信任与鼓励的有力见证。在此࿰…...
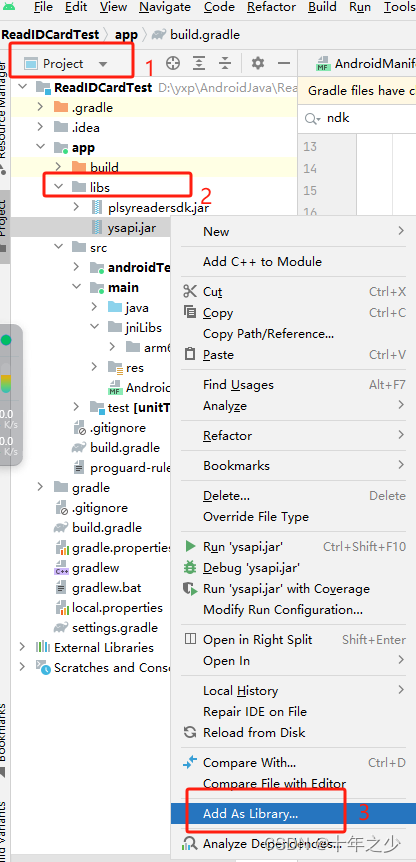
Android Studio导入第三方so库和jar包——Android Studio
导入so库 方式一(libs文件夹) 将项目以【Project】的结构显示,将目标架构对应的so文件夹(如下图中 的arm64-v8a)复制粘贴到app文件下的lib文件夹中(如下图的步骤1 2 3) 在build.gradle&…...
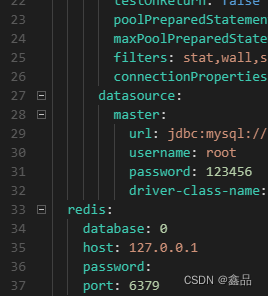
jeecg-boot 3.6使用微服务启动详细配置
1:运行sql文件 2:配置host 路径如下 127.0.0.1 jeecg-boot-redis 127.0.0.1 jeecg-boot-mysql 127.0.0.1 jeecg-boot-nacos 127.0.0.1 jeecg-boot-gateway 127.0.0.1 jeecg-boot-system 127.0.0.1 jeecg-boot-xxljob 127.0.0.1 jeecg-boot-rabbitmq 3…...

【Android】【root remount】【2】如何判断设备是否remount
前言 高版本的android设备,在remount之后,如果再进行ota升级,会产生异常,从而无法升级成功。 如何判断设备是否remount 当前已android 10 平台为例 当我们执行 adb remount 时,系统调用会调用到system/core/adb/dae…...

html中的“居中”问题详解(超全)
html中的“居中”问题详解(超全) 图片居中文本居中定位居中元素居中响应式设计中的居中技巧 引言: 在网页设计和开发中,实现元素的居中是一个常见但也常被低估的挑战。无论是在传统的网页布局中还是在响应式设计中,居中…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
