算法打卡day33
今日任务:
1)509. 斐波那契数
2)70. 爬楼梯
3)746.使用最小花费爬楼梯
509. 斐波那契数
题目链接:509. 斐波那契数 - 力扣(LeetCode)
斐波那契数,通常用 F(n) 表示,形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1 给你n ,请计算 F(n) 。示例 1: 输入:2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1示例 2: 输入:3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2示例 3: 输入:4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3提示: 0 <= n <= 30
文章讲解:代码随想录 (programmercarl.com)
视频讲解:手把手带你入门动态规划 | LeetCode:509.斐波那契数哔哩哔哩bilibili
思路:
- 首先定义一个列表
f来存储斐波那契数列的值,初始包含前两项 [0, 1]。- 如果 n 小于等于 1,则直接返回列表中对应位置的值。
- 否则,使用循环从 2 开始遍历到 n,依次计算每一项的值,并添加到列表
f中。- 最后返回列表中索引为 n 的值,即为斐波那契数列的第 n 项
class Solution:def fib(self, n: int) -> int:# 初始化斐波那契数列的前两项f = [0, 1]# 如果 n 小于等于 1,则直接返回对应位置的值if n <= 1:return f[n]# 使用循环计算斐波那契数列的第 n 项for x in range(2, n + 1):# 计算第 x 项的值,并添加到列表中f.append(f[x - 1] + f[x - 2])# 返回斐波那契数列的第 n 项return f[n]这种比较好理解,立马能想到,这里面可以优化的部分在空间复杂度,上面代码空间复杂度O(n)
我们可以定义一个长度为3的列表,反复更新这三个数即可。空间复杂度O(3)
也可以定义3个变量,反复更新3个变量。空间复杂度O(1)
class Solution:# 空间复杂度O(3)def fib(self, n: int) -> int:if n <= 1:return ndp = [0, 1]for i in range(2, n + 1):total = dp[0] + dp[1]dp[0] = dp[1]dp[1] = totalreturn dp[1]# 空间复杂度O(1)def fib(self, n: int) -> int:if n <= 1:return nprev1, prev2 = 0, 1for _ in range(2, n + 1):curr = prev1 + prev2prev1, prev2 = prev2, currreturn prev270. 爬楼梯
题目链接:70. 爬楼梯 - 力扣(LeetCode)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 注意:给定 n 是一个正整数。示例 1: 输入: 2 输出: 2 解释: 有两种方法可以爬到楼顶。 1 阶 + 1 阶 2 阶示例 2: 输入: 3 输出: 3 解释: 有三种方法可以爬到楼顶。 1 阶 + 1 阶 + 1 阶 1 阶 + 2 阶 2 阶 + 1 阶
文章讲解:代码随想录 (programmercarl.com)
视频讲解:带你学透动态规划-爬楼梯(对应力扣70.爬楼梯)| 动态规划经典入门题目哔哩哔哩bilibili
思路:
爬到第一层楼梯有一种方法,爬到二层楼梯有两种方法。
那么第一层楼梯再跨两步就到第三层 ,第二层楼梯再跨一步就到第三层。
所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来,那么就可以想到动态规划了。
- 首先定义一个列表
f来存储爬楼梯的方法数,初始包含前三项 [0, 1, 2]。其中 f[0] 为占位符,不参与计算。- 如果 n 小于 3,则直接返回列表中对应位置的值。
- 否则,使用循环从 3 开始遍历到 n,依次计算每一项的值,并添加到列表
f中。每一项的值都等于前两项和前一项的和,因为可以选择爬一阶或者爬两阶台阶。- 最后返回列表中索引为 n 的值,即为爬楼梯的方法数。
class Solution:def climbStairs(self, n: int) -> int:f = [0,1,2]if n < 3:return f[n]for x in range(3,n+1):f.append(f[x-1]+f[x-2])return f[n]# 空间复杂度为O(3)版本def climbStairs(self, n: int) -> int:if n <= 1:return nf = [0] * 3f[1] = 1f[2] = 2for i in range(3, n + 1):total = f[1] + f[2]f[1] = f[2]f[2] = totalreturn f[2]# 空间复杂度为O(1)版本def climbStairs2(self, n: int) -> int:if n <= 1:return nprev1 = 1prev2 = 2for i in range(3, n + 1):total = prev1 + prev2prev1 = prev2prev2 = totalreturn prev2746.使用最小花费爬楼梯
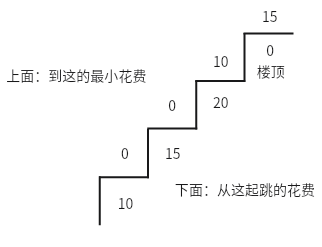
题目链接:746. 使用最小花费爬楼梯 - 力扣(LeetCode)
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。 请你找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。示例 1: 输入:cost = [10, 15, 20] 输出:15 解释:最低花费是从 cost[1] 开始,然后走两步即可到阶梯顶,一共花费 15 。示例 2: 输入:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 输出:6 解释:最低花费方式是从 cost[0] 开始,逐个经过那些 1 ,跳过 cost[3] ,一共花费 6 。提示: cost 的长度范围是 [2, 1000]。 cost[i] 将会是一个整型数据,范围为 [0, 999]
文章讲解:代码随想录 (programmercarl.com)
视频讲解:动态规划开更了!| LeetCode:746. 使用最小花费爬楼梯哔哩哔哩bilibili
思路:
用数组展示如下:
class Solution:def minCostClimbingStairs(self, cost: List[int]) -> int:# 如果台阶数小于2,则不需要花费if len(cost) < 2:return 0# 初始化到达前两个台阶的最低花费cost1 = 0cost2 = 0# 将顶部的台阶花费添加到列表中cost.append(0)# print(f'初始化cost1={cost1},cost2={cost2}')# 从第三个台阶开始计算最低花费for i in range(2, len(cost)):# 计算到达当前台阶的最低花费cost_total = min(cost1 + cost[i - 2], cost2 + cost[i - 1])# 更新前两个台阶的最低花费cost1 = cost2cost2 = cost_total# print(f'i={i},cost1={cost1},cost2={cost2},cost_total={cost_total}')# 返回到达顶部的最低花费return cost2相关文章:

算法打卡day33
今日任务: 1)509. 斐波那契数 2)70. 爬楼梯 3)746.使用最小花费爬楼梯 509. 斐波那契数 题目链接:509. 斐波那契数 - 力扣(LeetCode) 斐波那契数,通常用 F(n) 表示,形成…...
《疯狂java讲义》Java AWT图形化编程中文显示
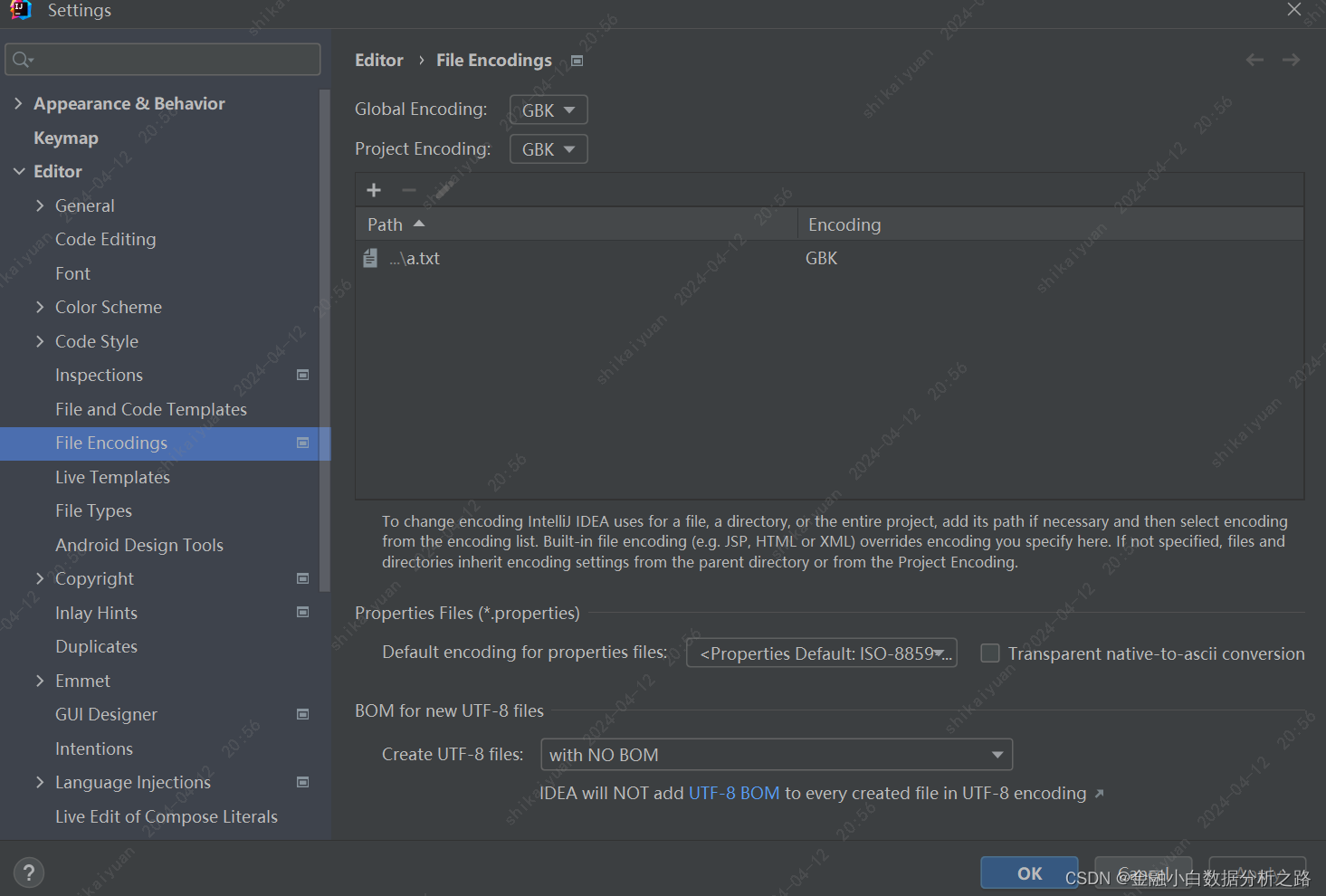
《疯狂java讲义》第六版第十一章AWT中文没有办法显示问题解决 VM Options设置为-Dfile.encodinggbk 需要增加变量 或者这边直接设置gbk 此外如果用swing 就不会产生这个问题了。...

Python3 标准库,API文档链接
一、标准库 即当你安装python3 后就自己携带的一些已经提供好的工具模块,工具类,可以专门用来某一类相关问题,达到辅助日常工作或者个人想法的一些成品库 类似的 C ,Java 等等也都有自己的标准库和使用文档 常见的一些: os 模块…...
【Web】CTFSHOW-ThinkPHP5-6反序列化刷题记录(全)
目录 web611 web612 web613-622 web623 web624-626 纯记录exp,链子不作赘述 web611 具体分析: ThinkPHP-Vuln/ThinkPHP5/ThinkPHP5.1.X反序列化利用链.md at master Mochazz/ThinkPHP-Vuln GitHub 题目直接给了反序列化入口 exp: <?ph…...

AR智能眼镜方案_MTK平台安卓主板芯片|光学解决方案
AR眼镜作为一种引人注目的创新产品,其芯片、显示屏和光学方案是决定整机成本和性能的关键因素。在这篇文章中,我们将探讨AR眼镜的关键技术,并介绍一种高性能的AR眼镜方案,旨在为用户带来卓越的体验。 AR眼镜的芯片选型至关重要。一…...
Android网络抓包--Charles
一、Android抓包方式 对Https降级进行抓包,降级成Http使用抓包工具对Https进行抓包 二、常用的抓包工具 wireshark:侧重于TCP、UDP传输层,HTTP/HTTPS也能抓包,但不能解密HTTPS报文。比较复杂fiddler:支持HTTP/HTTPS…...
)
【LeetCode热题100】238. 除自身以外数组的乘积(数组)
一.题目要求 给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 **不要使用除法,**且在…...
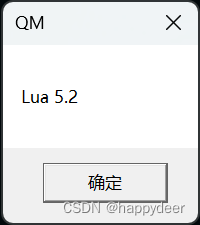
《哈迪斯》自带的Lua解释器是哪个版本?
玩过《哈迪斯》(英文名:Hades)吗?最近在研究怎么给这款游戏做MOD,想把它的振动体验升级到更高品质的RichTap。N站下载了一些别人做的MOD,发现很多都基于相同的格式,均是对游戏.sjon文件或.lua文…...

Java内存泄漏内存溢出
1.定义 OOM内存溢出是指应用程序尝试使用更多内存资源,而系统无足够的内存,导致程序崩溃。 内存泄漏是指应用程序中分配的内存未能被正确释放,导致系统中的可用内存逐渐减少。 2.内存泄漏的原因 可能包括对象引用未被释放、缓存未被清理等。 …...

【springboot】项目启动时打印全部接口方法
方法:在你springboot项目的基础上,创建下面的类: package com.llq.wahaha.listener;import org.springframework.beans.factory.annotation.Autowired; import org.springframework.context.ApplicationContext; import org.springframework…...

单例19c RMAN数据迁移方案
一、环境说明 源库 目标库 IP 192.168.37.200 192.168.37.202 系统版本 RedHat 7.9 RedHat 7.9 数据库版本 19.3.0.0.0 19.3.0.0.0 SID beg beg hostname beg rman 数据量 1353M 说明:源库已经创建数据库实例,并且存在用户kk和他创建的表空间…...
05—面向对象(上)
一、面向对象编程 1、类和对象 (1)什么是类 类是一类具有相同特性的事物的抽象描述,是一组相关属性和行为的集合。 属性:就是该事物的状态信息。行为:就是在你这个程序中,该状态信息要做什么操作&#x…...

【LeetCode热题100】【链表】两数相加
题目链接:2. 两数相加 - 力扣(LeetCode) 基本思路同:【leetcode】大数相加-CSDN博客 数值的位置已经倒过来了,用一个进位记录进位,用一个数记录和,链表到空了就当成0 class Solution { publi…...

Linux命令学习—linux 的硬件管理
1.1、linux 的硬件管理 1.1.1、计算机的硬件管理 在 linux 下,计算机所有设备是以文件的形势存在的。 在 linux 下查看硬件信息 ①、lspci 列出所有的 PCI 设备 ②、fdisk -l 查看存储设备信息 ③、查看/proc 目录下相应的文件来查看一些设备信息 cat /proc/cp…...

通讯录项目(用c语言实现)
一.什么是通讯录 通讯录是一种用于存储联系人信息的工具或应用程序。它是一种电子化的地址簿,用于记录和管理个人、机构或组织的联系方式,如姓名、电话号码、电子邮件地址和邮寄地址等。通讯录的目的是方便用户在需要时查找和联系他人。 通讯录通常以列…...

让大模型落地有“技”可循
“2018年,随着Transformer预训练模型的兴起,自然语言处理(NLP)学术圈中形成了一个主流观点——NLP领域的不同技术方向,如文本分类、文本匹配、序列标注等,最终都会被归结到文本生成这一核心任务之下。”这是…...
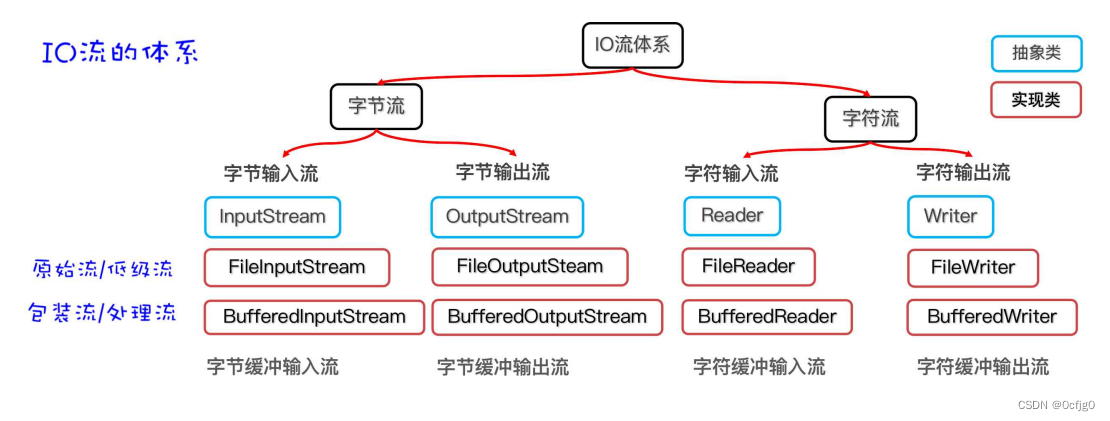
java:字符集和字符流
字符集 规定了字符和二进制之间对应关系的一张表 字节是计算机最基本的存储单位 字符则是通过字符组成和编码而成的文本 常见字符集 1,ASCII字符集 基础字符编码标准,包含128个字符,只包括英文字母,数字和一些常见的符号 一个字节表示一个字符 所有的字符集均兼容ASCII…...

Java常见的设计模式
Java常见的设计模式 工厂模式(Factory Pattern)单例模式(Singleton Pattern)代理模式模式(Proxy Pattern)适配器模式(Adapter Pattern)观察者模式(Observer Pattern&…...
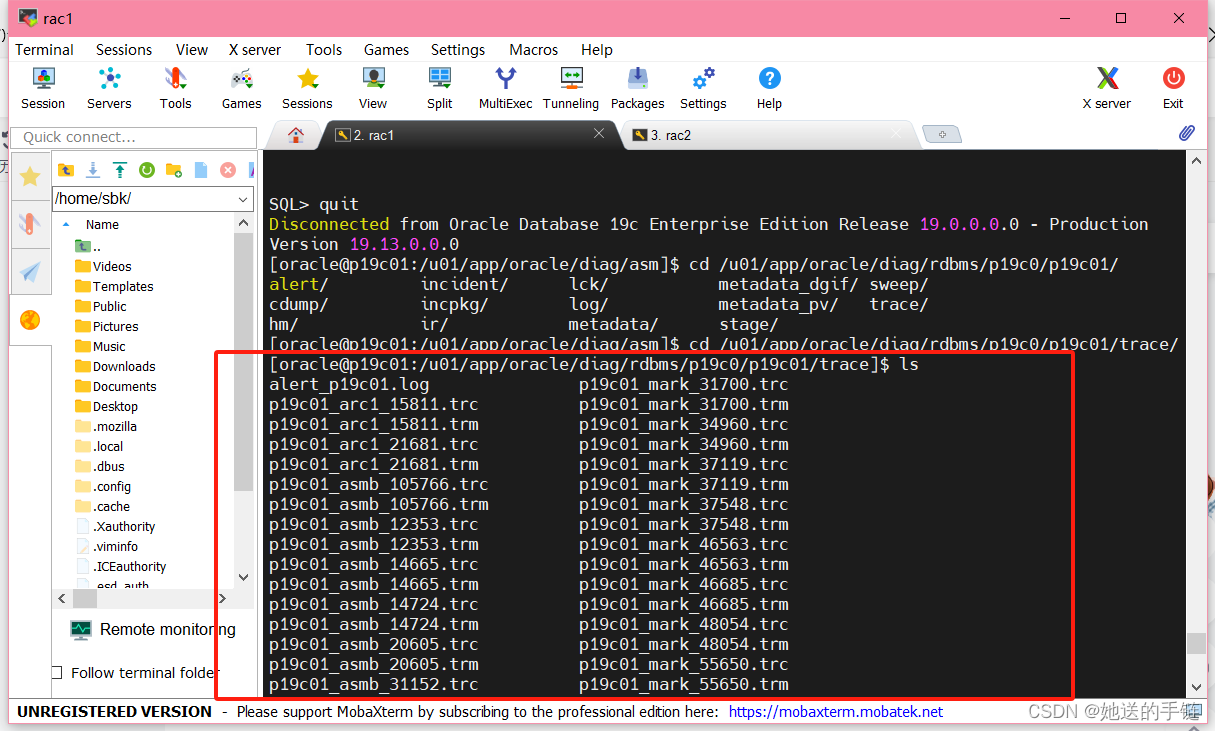
Oracle 19c RAC集群相关日志
1.DB日志(数据库日志) Redo Log(重做日志): 在Oracle数据库中,重做日志记录了数据库发生的所有修改操作,包括数据的插入,更新和删除。在RAC的环境中,每个实例都有自己的重…...
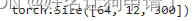
TR4 - Transformer中的多头注意力机制
目录 前言自注意力机制Self-Attention层的具体机制Self-Attention 矩阵计算 多头注意力机制例子解析 代码实现总结与心得体会 前言 多头注意力机制可以说是Transformer中最主要的模块,没有之一。这次我们来仔细分析一下注意力机制与多头注意力机制。 自注意力机制…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...

LeetCode 0386.字典序排数:细心总结条件
【LetMeFly】386.字典序排数:细心总结条件 力扣题目链接:https://leetcode.cn/problems/lexicographical-numbers/ 给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。 你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。…...
加密芯片与MCU协同工作的典型流程)
SE(Secure Element)加密芯片与MCU协同工作的典型流程
以下是SE(Secure Element)加密芯片与MCU协同工作的典型流程,综合安全认证、数据保护及防篡改机制: 一、基础认证流程(参数保护方案) 密钥预置 SE芯片与MCU分别预置相同的3DES密钥(Key1、Key2…...

Linux实现线程同步的方式有哪些?
什么是线程同步? 想象一下超市收银台:如果所有顾客(线程)同时挤向同一个收银台(共享资源),场面会一片混乱。线程同步就是给顾客们发"排队号码牌",确保: 有序访…...

每日一令:Linux 极简通关指南 - 汇总
专栏列表 💻 每日一令:Linux 极简通关指南 (25篇) 【基础】每天掌握一个Linux命令 - nsenter:深入容器与命名空间的利器 发布于 2025-06-08 22:27:04【基础】 每天掌握一个Linux命令 - journalctl:系统日志管理的得力助手 发布于…...