牛客周赛 Round 39(A,B,C,D,E,F,G)
比赛链接
官方题解(视频)
B题是个贪心。CD用同余最短路,预处理的完全背包,多重背包都能做,比较典型。E是个诈骗,暴力就完事了。F是个线段树。G是个分类大讨论,出题人钦定的本年度最佳最粪 题目
A 小红不想做炸鸡块粉丝粉丝题
思路:
签到
code:
#include <iostream>
#include <cstdio>
using namespace std;int a,tot;int main(){cin>>a;tot=a;for(int i=2,t;i<=6;i++)cin>>t,tot+=t;if(a*30>=tot)puts("No");else puts("Yes");return 0;
}
B 小红不想做鸽巢原理
思路:
emmmm不太清楚和鸽巢原理有啥关系,就是个贪心的思路。
因为是 k k k 个 k k k 个取走,所以假设一共有 t o t tot tot 个小球,最后会剩下 t o t % k tot\%k tot%k 个小球。因为要剩下的种类尽可能少,那么我们尽可能留下数量多的种类就行了。
code:
#include <iostream>
#include <cstdio>
#include <set>
using namespace std;
const int maxn=1e5+5;
typedef long long ll;int n,k;
ll tot=0;
set<int> S;int main(){cin>>n>>k;for(int i=1,t;i<=n;i++){cin>>t;S.insert(t);tot+=t;}tot%=k;if(tot==0){cout<<0<<endl;return 0;}int ans=0;for(auto it=S.rbegin();it!=S.rend();it++){ans++;if(tot>*it)tot-=*it;else break;}cout<<ans<<endl;return 0;
}
C,D 小红不想做完全背包
思路:
和寒假营第二场的D题是同种类型的题,做法有三:同余最短路,带预处理的完全背包,多重背包。
因为我们只想要是 p p p 的倍数,而这个数是什么我们不关心,所以我们用到的数都直接模 p p p 即可,当模 p p p 等于零的时候就是 p p p 的倍数了,这就算是比较典型板子 的带同余的完全背包问题了。
它和一般的完全背包还不太一样,普通的完全背包跑一趟就够了,因为重量不会无缘无故减少,我们只要从小到大跑一遍就能考虑到所有情况了,但是带同余的话重量就有可能减少了。比如容量为 7 7 7,物品的重量为 3 3 3,不带只跑一遍和带了跑到重复为止的结果是不一样的,如下图:
容量:0 1 2 3 4 5 6不带:0 0 1 0 0 2 0
带了:5 3 1 6 4 2 7
一般来说,我们从某个位置出发,为了跑到第一次重复,至少需要跑 p 2 g c d ( a i , p ) \dfrac {p^2}{gcd(a_i,p)} gcd(ai,p)p2 次(设 a i ∗ x ≡ a i ( m o d p ) a_i*x\equiv a_i\pmod p ai∗x≡ai(modp),解出来 x = p g c d ( a i , p ) + 1 x=\dfrac p{gcd(a_i,p)}+1 x=gcd(ai,p)p+1,也就是说一趟只用跑 p g c d ( a i , p ) \dfrac p{gcd(a_i,p)} gcd(ai,p)p 次就可以停了,再以每位置开始跑一趟,一共 p ∗ p g c d ( a i , p ) p*\dfrac p{gcd(a_i,p)} p∗gcd(ai,p)p 次)。再算上有 n n n 件物品,这样时间复杂度就爆了, 最坏情况 O ( n ∗ p 2 ) O(n*p^2) O(n∗p2)。
大致代码如下,TLE了(数据太弱了,居然就T了三个点,而且如果就算不枚举开始位置,只跑一次,甚至只WA三个点,经过某些神秘的顺序安排,居然还能AC,给人一种做法是正确的的错觉)
cin>>n>>p;vector<int> a(n);for(int i=0,t;i<n;i++){cin>>t;a[i]=t%p;}sort(a.begin(),a.end());a.erase(unique(a.begin(),a.end()),a.end());n=a.size();vector<int> dp(p+5,1e9);for(auto x:a){dp[x]=1;for(int idx=0;idx<p;idx++)for(int i=1,t=(idx+x)%p;i<p/gcd(x,p);i++,t=(t+x)%p)dp[(t+x)%p]=min(dp[(t+x)%p],dp[t]+1);}cout<<dp[0];
发现我们没必要从每个位置开始都跑 p g c d ( a i , p ) \dfrac p{gcd(a_i,p)} gcd(ai,p)p 次,我们用多个物品得到的重量是固定的,我们不如一开始就处理好,然后直接拿来用。具体来说,设 c s t [ i ] cst[i] cst[i] 表示增加重量为 i i i 需要使用多少个物品,多个物品可以都处理到一个 c s t [ i ] cst[i] cst[i],预处理的时间复杂度为 n ∗ p g c d ( a i , p ) n*\dfrac p{gcd(a_i,p)} n∗gcd(ai,p)p,使用的时候直接把 c s t [ i ] cst[i] cst[i] 当作物品跑完全背包,每个物品只跑一趟即可。
为什么预处理后不需要跑多趟了?原来我们用物品 a i a_i ai 跑第一次的时候,这时相当于用 c s t [ a i % p ] cst[a_i\%p] cst[ai%p] 跑一次,原来我们用物品 a i a_i ai 跑第二次的时候,这时相当于用 c s t [ 2 ∗ a i % p ] cst[2*a_i\%p] cst[2∗ai%p] 跑一次,原来我们用物品 a i a_i ai 跑第三次的时候,这时相当于用 c s t [ 3 ∗ a i % p ] cst[3*a_i\%p] cst[3∗ai%p] 跑一次,类推,甚至我们多个物品同时处理后,这个 c s t cst cst 值还会更小,答案更优。因此我们原本每个位置每个物品跑多次,现在只要每个位置每个 c s t cst cst 跑一次就可以了。
因此完全背包部分时间复杂度就优化为了 O ( p 2 ) O(p^2) O(p2)。总的时间复杂度就优化为了 O ( n ∗ p g c d ( a i , p ) + p 2 ) O(\dfrac {n*p}{gcd(a_i,p)}+p^2) O(gcd(ai,p)n∗p+p2),最坏 O ( n p + p 2 ) O(np+p^2) O(np+p2)。
另外同余最短路和多重背包也是正确的做法,数据弱,奇奇怪怪的做法也能日过去。
code:
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn=2005;int n,p;
int gcd(int a,int b){while(b)b^=a^=b^=a%=b;return a;
}int main(){cin>>n>>p;vector<int> a(n);for(int i=0,t;i<n;i++){cin>>t;a[i]=t%p;}sort(a.begin(),a.end());a.erase(unique(a.begin(),a.end()),a.end());n=a.size();vector<int> cst(p+5,1e9),dp(p+5,1e9);for(auto x:a){for(int i=1,cur=x;i<=p;i++,cur=(cur+x)%p){cst[cur]=min(cst[cur],i);}}for(int i=0;i<p;i++){int x=cst[i];//i步数 x代价 dp[i]=min(dp[i],x);for(int j=i;j<p+i;j++)dp[j%p]=min(dp[j%p],dp[(j-i+p)%p]+x);}cout<<dp[0];return 0;
}
E 小红不想做莫比乌斯反演杜教筛求因子和的前缀和
思路:
之前练习赛出了一个名字差不多的题,特难。这次出题人估计是想骗做题人给自己上压力,不过可惜放在了 E E E 题的位置上。没骗到。
枚举长 n n n 和宽 m m m,然后算出 p p p,统计答案个数即可。
code:
#include <iostream>
#include <cstdio>
using namespace std;int n,m,p,x;
int ans=0;int main(){cin>>n>>m>>p>>x;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)if((x-i*j)%(2*(i+j))==0 && (x-i*j)/(2*(i+j))>=1 && (x-i*j)/(2*(i+j))<=p)ans++;cout<<ans;return 0;
}
F 小红不想做模拟题
思路:
区间修改,区间查询,还是比较明显能想到线段树的。
当我们区间推平时,比如推平了 a a a 串的区间 [ l , r ] [l,r] [l,r],把它变成 1 1 1,那么这一段区间 1 1 1 的对数就变成了 b b b 串这段区间中 1 1 1 的个数,同理推平另一个串。所以我们为了维护区间 1 1 1 的对数,还需要分别维护住 a , b a,b a,b 串区间内 1 1 1 的个数。
另外因为这个题只进行了一个简单的推平操作,所以我们也不需要写懒节点并将节点信息向下传递,我们只要在线段树节点上打个标记,表示是否推平了,之后修改或者查询的时候查到标记就直接返回就行了。
code:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=1e5+5;int n,q;
string str[2];struct segment_tree{#define ls p<<1#define rs p<<1|1struct Node{int l,r;int a,b;//区间内 a串1的个数,b串1的个数int sam;//ab串同为1的位置的个数bool fa,fb;//是否填平Node(int l=0,int r=0,int a=0,int b=0,int sam=0,bool fa=false,bool fb=false):l(l),r(r),a(a),b(b),sam(sam),fa(fa),fb(fb){}; }tr[maxn<<4];void push_up(int p){auto& [l,r,a,b,sam,fa,fb]=tr[p];a=(fa)?r-l+1:tr[ls].a+tr[rs].a;b=(fb)?r-l+1:tr[ls].b+tr[rs].b;if(fa)sam=tr[p].b;else if(fb)sam=tr[p].a;else sam=tr[ls].sam+tr[rs].sam;}void build(int p,int l,int r){tr[p].l=l;tr[p].r=r;if(l==r){tr[p].a=(str[0][l-1]=='1');tr[p].b=(str[1][l-1]=='1');tr[p].sam=(tr[p].a && tr[p].b);return;}int mid=l+r>>1;build(ls,l,mid);build(rs,mid+1,r);push_up(p);}void print(int p,int l,int r){printf("%d [%d,%d]:%d %d %d\n",p,l,r,tr[p].a,tr[p].b,tr[p].sam);if(l==r){return;}int mid=l+r>>1;print(ls,l,mid);print(rs,mid+1,r);}void print(){print(1,1,n);}void modify(int p,int l,int r,int L,int R,bool st){if(L<=l && r<=R){if(st){//填平a串 tr[p].a=r-l+1;tr[p].fa=true;tr[p].sam=tr[p].b;}else {//填平b串 tr[p].b=r-l+1;tr[p].fb=true;tr[p].sam=tr[p].a;}return;}int mid=l+r>>1;if(mid>=L)modify(ls,l,mid,L,R,st);if(mid<R)modify(rs,mid+1,r,L,R,st);push_up(p);}int q(){return tr[1].sam;}#undef ls#undef rs
}tr;int main(){
// cin.tie(0)->sync_with_stdio(false);cin>>n>>str[0]>>str[1];tr.build(1,1,n);for(cin>>q;q;q--){char ch;int l,r;cin>>ch>>l>>r;tr.modify(1,1,n,l,r,(ch=='A'));cout<<tr.q()<<endl;
// tr.print();
// cout<<endl;}return 0;
}
G 小红不想做平衡树
思路:
我们发现,在一个数列里,数列一定是升序段降序段交替出现的,比如:升序-降序-升序-降序…,或者 降序-升序-降序-升序…。
我们选择一段区间,然后翻转其某个子段,使得反转后成为一个升序序列,有五种可能的情况(因为题目保证了数列中数各不相同,所以这里不讨论数值相等的情况,下面默认如此):
- 整段升序。
- 整段降序。
- 先升序,后降序。而且第一段最大值小于第二段最小值。
- 先降序,后升序。而且第一段最大值小于第二段最小值。
- 先升序,后降序,再升序。第一段最大值小于第二段最小值,且第二段最大值小于第三段最小值。
大概示例图如下:

我们对每种情况分别讨论,然后统计答案即可。
不过实际在写的时候会非常麻烦,因为前一段的末尾那个数正好就是后一段开头的那个数,导致上面的五种情况会出现重叠计数的情况。比如第三种情况中,第二段只取第一个数时,统计出来的答案就会和第一种情况完全重复,再比如第五种情况中第一段只选第一个数时统计出来的答案都和第四种情况出现重复等。在官方题解的写法中,细节也是蛮多的。下面只讲我的写法,和题解不太一样。
回到开头,在一个数列里,数列一定是升序段降序段交替出现的,而升序段和降序段交界处的那个数是两段共用的。这种“转折点”有两种类型:升序变降序(形如 ^),降序变升序(形如 √)。而且是交替出现的。
我们可以把这些转折点处理出来,然后根据转折点来统计答案。虽然仍然会出现重复的情况,但是更直观一些(大概?)
code:
#include <iostream>
#include <cstdio>
#include <vector>
#define pii pair<int,int>
using namespace std;
typedef long long ll;
const int maxn=2e5+5;int n,a[maxn];int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];ll ans=0;int st=-1;//第一个 ^ 点的位置vector<int> ver;for(int i=2,f;i<n;i++){f=-1;if(a[i-1]<a[i] && a[i]>a[i+1])f=0;// ^if(a[i-1]>a[i] && a[i]<a[i+1])f=1;// √if(!~st)st=f;if(~f)ver.push_back(i);}int tl=1,len,tn=ver.size();//1 2for(auto i:ver){len=i-tl+1;ans+=1ll*(len+1)*len/2;tl=i;}len=n-tl+1;ans+=1ll*(len+1)*len/2;ans-=tn;for(int i=st,id,l,r;i<ver.size();i+=2){//3id=ver[i];l=(i==0)?1:ver[i-1];r=(i==ver.size()-1)?n:ver[i+1];for(int j=id+1;j<=r;j++){//这边从id+1的位置开始统计,当j=id时会和情况2重复if(a[j]>a[id-1])ans+=id-l;else break;}}for(int i=st^1,id,l,r;i<ver.size();i+=2){//4id=ver[i];l=(i==0)?1:ver[i-1];r=(i==ver.size()-1)?n:ver[i+1];for(int j=id-1;j>=l;j--){//这边从id-1的位置开始统计,当j=id时会和情况1重复if(a[j]<a[id+1])ans+=r-id;else break;}}for(int i=st,id1,id2,l,r;i+1<ver.size();i+=2){//5id1=ver[i];id2=ver[i+1];l=(i==0)?1:ver[i-1];r=(i+1==ver.size()-1)?n:ver[i+2];if(a[id1-1]<a[id2] && a[id1]<a[id2+1])ans+=1ll*(id1-l)*(r-id2);}cout<<ans<<endl;return 0;
}
相关文章:

牛客周赛 Round 39(A,B,C,D,E,F,G)
比赛链接 官方题解(视频) B题是个贪心。CD用同余最短路,预处理的完全背包,多重背包都能做,比较典型。E是个诈骗,暴力就完事了。F是个线段树。G是个分类大讨论,出题人钦定的本年度最佳最粪 题目…...

解锁区块链技术的潜力:实现智能合约与DApps
在数字时代,区块链技术正迅速成为重塑多个行业的革命性力量。从金融服务到供应链管理,再到数字身份验证,区块链提供了一种去中心化、安全和透明的数据处理方式。在本文中,我们将深入探讨区块链技术,特别是智能合约和去…...

MAC OS关闭SIP(navicat 无法保存密码)
最近安装navicat(16.3.7)时,安装后无法保存密码,保存密码会报错如下: 因为用的破解版,一开始是打不开的,用自带的修复软件修复后就可以打开了,但是保存密码就会报错,按照网上的一些操作 1、卸载…...

阿里云服务器带宽价格全解析,附报价单
阿里云服务器公网带宽怎么收费?北京地域服务器按固定带宽计费一个月23元/M,按使用流量计费0.8元/GB,云服务器地域不同实际带宽价格也不同,阿里云服务器网aliyunfuwuqi.com分享不同带宽计费模式下带宽收费价格表: 公网…...
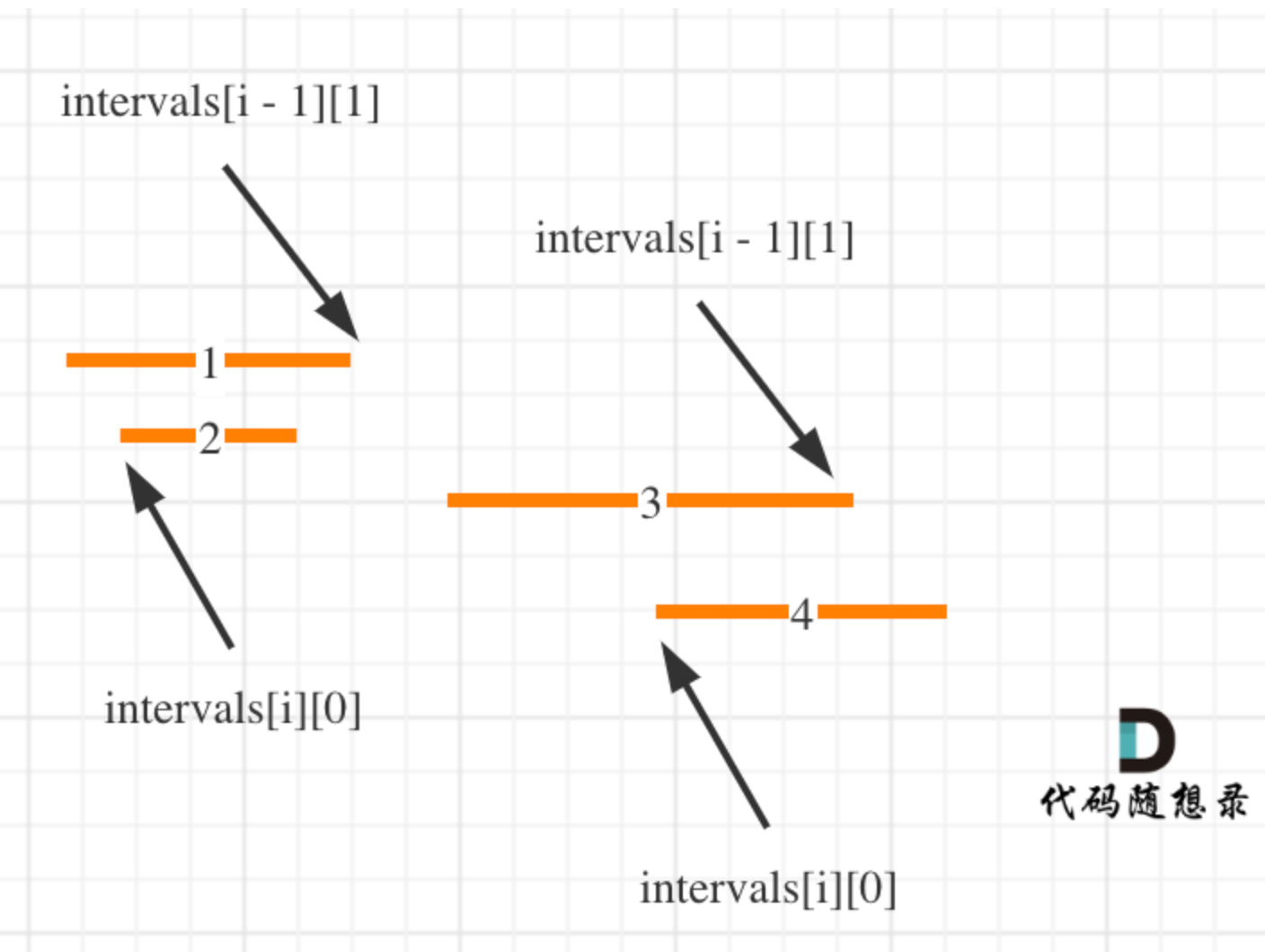
Day36|贪心算法part05:435. 无重叠区间、763.划分字母区间、56. 合并区间
435. 无重叠区间 有了上题射气球的因子,这题也就有思路了,反正无脑排序就行了: 首先将所有区间按照end的大小从小到大排序;选取最早end为起始x_end遍历所有区间,如果该区间的start比end大(可重叠…...

棋牌室计时吧台计费收费灯控管理系统软件操作流程
棋牌室计时吧台计费收费灯控管理系统软件操作流程 一、前言 以下软件操作教程以,佳易王棋牌桌球计时计费管理系统软件灯控版V17.87为例说明 软件文件下载可以点击最下方官网卡片——软件下载——试用版软件下载 该计时计费软件可以是棋牌和桌球混合同时计时计费 …...

【实践篇】RabbitMQ实现队列延迟功能汇总
前言 记录下RabbitMQ实现延迟队列功能的所有实践内容。 前期准备,需要安装好docker、docker-compose的运行环境。 一、安装RabbitMQ 开启RabbitMQ的WEB管理功能。-CSDN博客 二、实现延迟队列的两种方式 RabbitMQ实现延迟队列的两种方式。-CSDN博客 三、实践文…...

EditPlus来啦(免费使用!)
hello,我是小索奇 今天推荐一款编辑器,是索奇学习JavaSE时入手滴,非常好用哈,小索奇还是通过老杜-杜老师入手滴,相信很多人也是通过老杜认识嘞,来寻找破解版或者准备入手这个间接使用的编辑器~ EditPlus是…...

蓝桥杯22年第十三届省赛-数组切分|线性DP
题目链接: 蓝桥杯2022年第十三届省赛真题-数组切分 - C语言网 (dotcpp.com) 1.数组切分 - 蓝桥云课 (lanqiao.cn) 这道题C语言网数据会强一些。 说明: 对于一个切分的子数组,由于数组是1-N的一个排列,所以每个数唯一 可以用子…...
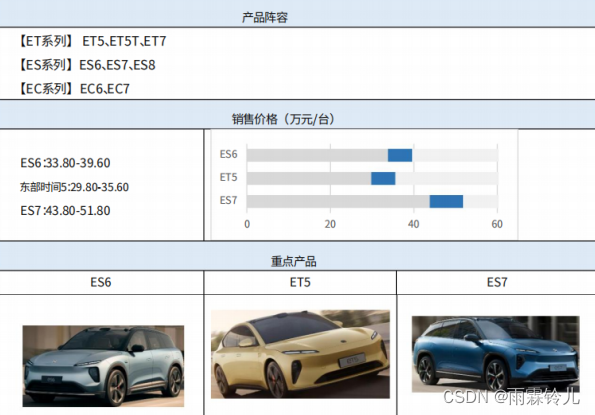
小米汽车:搅动市场的鲶鱼or价格战砧板上的鱼肉?
3月28日晚,备受关注的小米汽车上市发布会召开,小米集团董事长雷军宣布小米SU7正式发布。小米汽车在带飞股价的同时,二轮订购迅速售尽。 图一:小米集团股价 雷军口中“小米汽车迈出的第一步,也是人生最后一战的开篇”&a…...

Docker 学习笔记(五):梳理 Docker 镜像知识,附带 Commit 方式提交镜像副本,安装可视化面板 portainer
一、前言 记录时间 [2024-4-10] 前置文章: Docker学习笔记(一):入门篇,Docker概述、基本组成等,对Docker有一个初步的认识 Docker学习笔记(二):在Linux中部署Docker&…...
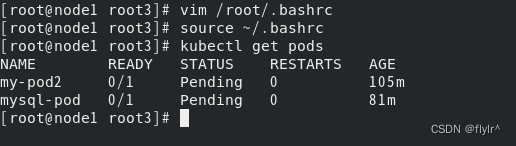
K8S node节点执行kubectl get pods报错
第一个问题是由第二个问题产生的,第二个问题也是最常见的 网上找的都是从master节点把文件复制过来,这样确实可以解决,但是麻烦,有一个node节点还好,如果有多个呢?每个都复制吗?下面是我从外网…...

C++简单日志系统
需求描述 日志等级:定义一个枚举类型 LogLevel,包含至少四个等级:DEBUG、INFO、WARNING、ERROR。日志记录:实现一个 Logger 类,包含以下功能: 一个静态方法 log,接受 LogLevel 和一个字符串作为…...

MySQL基础练习题:习题21-25
这部分主要是为了帮助大家回忆回忆MySQL的基本语法,数据库来自于MySQL的官方简化版,题目也是网上非常流行的35题。这些基础习题基本可以涵盖面试中需要现场写SQL的问题。 列出在部门sales工作的员工的姓名,假定不知道销售部的部门编号 sele…...

全面的网络流量监控
流量监控指的是对数据流进行的监控,通常包括出数据、入数据的速度、总流量。通过网络流量监控,组织可以确保只有业务关键型流量通过网络传输,并限制不需要的网络流量,从而提高网络效率,又可以防止停机、减少 MTTR、帮助…...

探索网络爬虫:技术演进与学习之路
网络爬虫及IP代理池 前言爬虫技术的演进最新的爬虫技术爬虫技术学习路线 前言 在信息时代,网络爬虫技术作为获取和处理网络数据的重要手段,已经成为数据科学、机器学习和许多商业应用的基石。从简单的HTML页面抓取到复杂的动态内容采集,爬虫…...

目标检测——色素性皮肤病数据集
一、重要性及意义 首先,色素性皮肤病变是一类常见的皮肤疾病,其发病率有逐年增高的趋势。这些病变可能由遗传或环境因素导致黑素细胞生成异常,如黑色素瘤等。黑色素瘤具有极高的恶性率和致死率,而且恶化可能性大,容易…...

Unity3D 打空包与远程资源更新详解
前言 在游戏开发过程中,打包和远程资源更新是非常重要的步骤,本文将详细介绍Unity3D中如何进行打空包和远程资源更新。 对惹,这里有一个游戏开发交流小组,希望大家可以点击进来一起交流一下开发经验呀! 一、打空包 …...

32单片机入门持续更新中
配套资料为野火霸道V2 初识 STM32 4.1 什么是 STM32 STM32,从字面上来理解,ST 是意法半导体,M 是 Microelectronics 的缩写,32 表示 32 位,合起 来理解,STM32 就是指 ST 公司开发的 32 位微控制器。在如今…...

蓝桥杯 每天2题 day6
碎碎念:哇咔咔 要不是中间缺勤一天就圆满day7了!最后一晚上!写题复习哇咔咔 唉,睡了一觉就看不下去了,,,看看之前的笔记洗洗睡觉,,, 记得打印准考证带好东西…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
