蓝桥杯【第15届省赛】Python B组
这题目难度对比历届是相当炸裂的简单了……
A:穿越时空之门
【问题描述】
随着 2024 年的钟声回荡,传说中的时空之门再次敞开。这扇门是一条神秘的通道,它连接着二进制和四进制两个不同的数码领域,等待着勇者们的探索。
在二进制的领域里,勇者的力量被转换成了力量数值的二进制表示中各数位之和。
在四进制的领域里,力量的转换规则相似,变成了力量数值的四进制表示中各数位之和。
穿越这扇时空之门的条件是严苛的:当且仅当勇者在二进制领域的力量等同于四进制领域的力量时,他才能够成功地穿越。
国王选定了小蓝作为领路人,带领着力量值从 1 到 2024 的勇者们踏上了这段探索未知的旅程。作为小蓝的助手,你的任务是帮助小蓝计算出,在这 2024 位勇者中,有多少人符合穿越时空之门的条件。
【解析及代码】
省流:数字转成二进制、四进制,数位之和相等的数
答案:63
cnt = 0
for i in range(1, 2025):# 二进制bins = bin(i)[2:].count("1")# 四进制four = 0while i:four += i % 4i //= 4# 累加cnt += bins == four
print(cnt)B:数字串个数
【问题描述】
小蓝想要构造出一个长度为 10000 的数字字符串,有以下要求:
1) 小蓝不喜欢数字 0 ,所以数字字符串中不可以出现 0 ;
2) 小蓝喜欢数字 3 和 7 ,所以数字字符串中必须要有 3 和 7 这两个数字。
请问满足题意的数字字符串有多少个?这个数字会很大,你只需要输出其 对 取余后的结果。
【解析及代码】
容斥原理秒杀
答案:157509472
mod = int(1e9 + 7)
n = 10000
cnt = pow(9, n, mod)
# 去除 no(3) + no(7) 的情况
cnt -= 2 * pow(8, n, mod)
# 补上 no(3 and 7) 的情况
cnt += pow(7, n, mod)
cnt %= mod
print(cnt)C:连连看
【问题描述】
小蓝正在和朋友们玩一种新的连连看游戏。在一个 n × m 的矩形网格中, 每个格子中都有一个整数,第 i 行第 j 列上的整数为 。玩家需要在这个网 格中寻找一对格子
使得这两个格子中的整数
和
相等,且 它们的位置满足
。请问在这个 n × m 的矩形网格中有多少对 这样的格子满足条件。
【输入格式】
输入的第一行包含两个正整数 n, m ,用一个空格分隔。
接下来 n 行,第 i 行包含 m 个正整数 ,相邻整数之间使 用一个空格分隔。
【输出格式】
输出一行包含一个整数表示答案。
【样例】
| 输入 | 输出 | 说明 |
| 3 2 1 2 2 3 3 2 | 6 | 一共有以下 6 对格子: (1, 2) − (2, 1) ,(2, 2) − (3, 1) , (2, 1) − (3, 2) ,(2, 1) − (1, 2) , (3, 1) − (2, 2) ,(3, 2) − (2, 1) 。 |
【评测用例规模与约定】
| 20% | |
| 100% |
【解析及代码】
根据题意可知,(a, b) - (c, d) 中的两个元素位于同一斜线上
(1, 2) - (2, 1) 和 (2, 1) - (1, 2) 算不同的两对,优化一下比较流程计算结果即可
n, m = map(int, input().split())
A = [list(map(int, input().split())) for _ in range(n)]# A[a][b] = A[c][d], 处于同一斜线上
cnt = 0
for i in range(n):for j in range(m):# 只跟当前行以下的行比较# 向左下角for p in range(1, min(n - i, j + 1)):cnt += A[i][j] == A[i + p][j - p]# 向右下角for p in range(1, min(n - i, m - j)):cnt += A[i][j] == A[i + p][j + p]
print(cnt * 2)D:神奇闹钟
【问题描述】
小蓝发现了一个神奇的闹钟,从纪元时间(1970 年 1 月 1 日 00:00:00 )开 始,每经过 x 分钟,这个闹钟便会触发一次闹铃(纪元时间也会响铃)。这引起 了小蓝的兴趣,他想要好好研究下这个闹钟。
对于给出的任意一个格式为 yyyy-MM-dd HH:mm:ss 的时间,小蓝想要 知道在这个时间点之前(包含这个时间点)的最近的一次闹铃时间是哪个时间?
注意,你不必考虑时区问题。
【输入格式】
输入的第一行包含一个整数 T,表示每次输入包含 T 组数据。
接下来依次描述 T 组数据。
每组数据一行,包含一个时间(格式为 yyyy-MM-dd HH:mm:ss)和一 个整数 x ,其中 x 表示闹铃时间间隔(单位为分钟)。
【输出格式】
输出 T 行,每行包含一个时间(格式为 yyyy-MM-dd HH:mm:ss),依次表示每组数据的答案。
【样例】
| 输入 | 输出 |
| 2 2016-09-07 18:24:33 10 2037-01-05 01:40:43 30 | 2016-09-07 18:20:00 2037-01-05 01:30:00 |
【评测用例规模与约定】
| 100% |
【解析及代码】
What can I say?
import timefmt = "%Y-%m-%d %H:%M:%S"
for _ in range(int(input())):datetime, x = input().rsplit(maxsplit=1)x = int(x) * 60t = round(time.mktime(time.strptime(datetime, fmt)))print(time.strftime(fmt, time.localtime(t - t % x)))
E:蓝桥村的真相
【问题描述】
在风景如画的蓝桥村,n 名村民围坐在一张古老的圆桌旁,参与一场思想 的较量。这些村民,每一位都有着鲜明的身份:要么是誉满乡野的诚实者,要 么是无可救药的说谎者。
当会议的钟声敲响,一场关于真理与谬误的辩论随之展开。每位村民轮流 发言,编号为 i 的村民提出了这样的断言:坐在他之后的两位村民——也就是 编号 i + 1 和 i + 2(注意,编号是环形的,所以如果 i 是最后一个,则 i + 1 是 第一个,以此类推)之中,一个说的是真话,而另一个说的是假话。
在所有摇曳不定的陈述中,有多少真言隐藏在谎言的面纱之后?
请你探索每一种可能的真假排列组合,并计算在所有可能的真假组合中, 说谎者的总数。
【输入格式】
输入的第一行包含一个整数 T,表示每次输入包含 T 组数据。
接下来依次描述 T 组数据。
每个数据一行包含一个整数 n,表示村落的人数。
【输出格式】
输出 T 行,每行包含一个整数,依次表示每组数据的答案。
【样例】
| 输入 | 输出 | 说明 |
| 2 3 3 | 6 6 | 可能的组合有 「假,假,假」「真,真,假」 「真,假,真」「假, 真,真」 说谎者的总数为 3 + 1 + 1 + 1 = 6。 |
【评测用例规模与约定】
| 10% | |
| 40% | |
| 100% |
【解析及代码】
1 表谎言,0 表真言,每 3 个人可能的组合有:010, 001, 100, 111
前三种情况:100 是一个循环,如果 n 能被 3 整除,这三种情况就贡献了 n 个说谎的
第三种情况:全都是 111,贡献了 n 个说谎的
for _ in range(int(input())):n = int(input())print(n * (1 + (n % 3 == 0)))
F:魔法巡游
【问题描述】
在蓝桥王国中,两位魔法使者,小蓝与小桥,肩负着维护时空秩序的使命。 他们每人分别持有 N 个符文石,这些石头被赋予了强大的力量,每一块上都刻 有一个介于 1 到 之间的数字符号。小蓝的符文石集合标记为
, 小桥的则为
。
两位魔法使者的任务是通过使用符文石,在各个时空结点间巡游。每次巡游遵循这样一条法则:当小蓝使用了符文石 到达新的结点后,小桥必须选用 一个序号更大的符文石(即某个
满足 j > i)前往下一个结点。同理,小桥抵 达之后,小蓝需要选择一个序号 k > j 的符文石
继续他们的巡游。
为了成功地穿梭时空,两个连续使用的符文石上的数字符号必须有共鸣, 这种共鸣只有当数字符号中至少包含一个特定的元素——星火(数字 0)、水波 (数字 2)或者风语(数字 4)时,才会发生。例如,符号序列 126, 552, 24, 4 中 的每对连续符文都包含了至少一个共鸣元素,则它们是一系列成功的巡游;而 如果是 15, 51, 5,则不成立,因为它们之间的共鸣元素不包含星火、水波或风语 中的任意一个。
小蓝总是先启程,使用他的符文石开启巡游。
你的任务是计算这对魔法使者能够执行的最长时空巡游序列的长度。这样 的序列形式为 ,其中序列索引满足
,并且序列中每一对相邻的符文石都至少包含一个共鸣元素。
【输入格式】
输入的第一行包含一个整数 N,表示每位魔法使者持有的符文石数量。
第二行包含 N 个整数 ,相邻整数之间使用一个空格分隔,表示小蓝的符文石上刻有的数字符号。
第三行包含 N 个整数 ,相邻整数之间使用一个空格分隔,表示小桥的符文石上刻有的数字符号。
【输出格式】
输出一行包含一个整数,表示小蓝和小桥在遵守所有规则的情况下,最多能进行多少次时空巡游。
【样例】
| 输入 | 输出 | 说明 |
| 5 126 393 581 42 44 204 990 240 46 52 | 4 | 小蓝和小桥可以选择以下符文石序列进行巡游:
这里,数字 2 作为共鸣元素连接了 |
【评测用例规模与约定】
| 30% | |
| 100% |
【解析及代码】
编写类 Element,重写 __init__ 方法以搜集符文石的特定元素,存储到 set 中
存储非空的 Element 的索引,结合 bisect 的二分查找加速枚举,直接动态规划
import bisectclass Element(set):base = {"0", "2", "4"}def __init__(self, s):super().__init__(set(s) & self.base)n = int(input())
e_lan = list(map(Element, input().split()))
e_qiao = list(map(Element, input().split()))# 编制非空元素的索引
i_lan = [i for i in range(n) if e_lan[i]]
i_qiao = [i for i in range(n) if e_qiao[i]]if not (i_lan and i_qiao):print(1)
# 两者都非空
else:# 小蓝先出发dp = [[0, 0] for _ in range(n)]for i in i_lan: dp[i][0] = 1res = 0for i in sorted(set(i_lan + i_qiao)):j_lan = bisect.bisect_left(i_lan, i)j_qiao = bisect.bisect_left(i_qiao, i)# 小蓝出发if i_lan[j_lan] == i:for src in i_qiao[:j_qiao]:if e_qiao[src] & e_lan[i]:dp[i][0] = max(dp[i][0], dp[src][1] + 1)# 小桥出发if i_qiao[j_qiao] == i:for src in i_lan[:j_lan]:if e_lan[src] & e_qiao[i]:dp[i][1] = max(dp[i][1], dp[src][0] + 1)res = max(res, max(dp[i]))print(res)
G:缴纳过路费
【问题描述】
在繁华的商业王国中,N 座城市被 M 条商路巧妙地连接在一起,形成了一 个错综复杂的无向图网络。每条商路是双向通行的,并且任意两座城市之间最 多只有一条直接的商路。每条商路都有它的规则,其中最引人注目的就是穿过商路,需要缴纳过路费。因此,商人们在选择商路时必须格外认真。
有一位名叫小蓝的商人,他对于商路的花费有着自己独到的见解。在小蓝 眼中,一条路线包含一条或多条商路,但路线的成本并不是沿途累积的过路费 总和,而是这条路线上最贵的那一次收费。这个标准简单而直接,让他能迅速 评估出一条路线是否划算。
于是,他设立了一个目标,即找出所有城市对,这些城市之间的最低路线 成本介于他心中预设的两个数 L 和 R 之间。他相信,这样的路线既不会太廉 价,以至于路况糟糕;也不会过于昂贵,伤害他精打细算的荷包。
作为小蓝的助手,请你帮助小蓝统计出所有满足条件的城市对数量。
【输入格式】
输入的第一行包含四个整数 N, M, L, R,表示有 N 座城市和 M 条双向通行 的商路,以及小蓝心中预设的最高过路费的下限 L 和上限 R。
接下来 M 行,每行包含三个整数 u, v, w,表示城市 u 和城市 v 之间有一条 双向通行的商路,过路费为 w。保证每对城市之间最多只有一条直接的商路。
【输出格式】
输出一行包含一个整数,表示满足条件的城市对数量。
【样例】
| 输入 | 输出 | 说明 |
| 5 5 1 2 1 2 2 1 3 5 1 4 1 2 4 5 2 5 4 | 3 | 满足条件的城市对有 (1, 2),(1, 4),(2, 4) |
【评测用例规模与约定】
| 30% | |
| 100% | |
【解析及代码】
如果用邻接矩阵的话,太稀疏了,所以用邻接表 + Floyd 算法解决
n, m, l, r = map(int, input().split())# 邻接表 (adj[0] 不使用, adj[n] 不需要)
adj = [{} for _ in range(n)]
for _ in range(m):u, v, w = map(int, input().split())adj[u][v] = wdef floyd(adj):inf = float("inf")def handler(i, m, wim):# j < mfor j in filter(i.__ne__, range(m)):if adj[j].get(m, 0):a, b = sorted((i, j))adj[a][b] = min(adj[a].get(b, inf), max(adj[j][m], wim))# j > mfor j in filter(i.__ne__, range(m + 1, n)):if adj[m].get(j, 0):a, b = sorted((i, j))adj[a][b] = min(adj[a].get(b, inf), max(adj[m][j], wim))for m in range(n):# i < mfor i in range(m):if adj[i].get(m, 0):handler(i, m, adj[i][m])# i > mfor i in range(m + 1, n):if adj[m].get(i, 0):handler(i, m, adj[m][i])floyd(adj)
cnt = 0
for i in range(n):for w in adj[i].values():cnt += l <= w <= r
print(cnt)H:纯职业小组
【问题描述】
在蓝桥王国,国王统治着一支由 n 个小队组成的强大军队。每个小队都由相同职业的士兵组成。具体地,第 i 个小队包含了 名职业为
的士兵。
近日,国王计划在王宫广场举行一场盛大的士兵检阅仪式,以庆祝王国的繁荣昌盛。然而,在士兵们入场的过程中,一场突如其来的风暴打乱了他们的 行列,使得不同小队的士兵混杂在一起,次序乱成一团,
尽管国王无法知道每个士兵的具体职业,但为了确保仪式能顺利进行,国王打算从这些混乱的士兵中选出一部分,组成 k 个“纯职业小组”进行检阅。 一个“纯职业小组”定义为由 3 名同职业的士兵组成的队伍。
请问,国王至少需要选择多少名士兵,才能确保这些士兵可以组成 k 个 “纯职业小组”。
【输入格式】
输入的第一行包含一个整数 T,表示每次输入包含 T 组数据。
接下来依次描述 T 组数据。
每组数据的第一行包含两个整数 和 k ,用一个空格分隔,表示小队的数量和要组成的纯职业小组的数量。
接下来的 行,每行包含两个整数
和
,用一个空格分隔,表示第 i 个小队中士兵的职业和数量。
【输出格式】
输出 T 行,每行包含一个整数,依次表示每组数据的答案,即为了组成 k 个“纯职业小组”,国王至少需要选择的士兵数量。如果无论如何也无法组成 k 个“纯职业小组”,则输出 −1。
【样例】
| 输入 | 输出 | 说明 |
| 2 3 2 1 3 2 3 3 3 3 5 1 3 2 3 3 3 | 8 -1 | 在第一个样例中,要想组成 2 个“纯职业小组”, 国王至少需要选择 8 名士兵。若只选择了 7 名士兵, 则这 7 名士兵的职业可能为 1, 1, 1, 2, 2, 3, 3, 无法组成 2 个“纯职业小组”。 在第二个样例中,即使选择了所有士兵, 也无法组成 5 个“纯职业小组”, 因此输出 −1。 |
【评测用例规模与约定】
| 50% | |
| 100% |
【解析及代码】
比方说有 8 个职业,每种职业有 3 个人,需要 5 个小组
最坏的情况下,会先分别在 8 个职业分别取 2 个人,然后才在 5 个职业里分别取 1 个人凑齐,以此类推
(考虑不周,待订正)
from collections import Counterdef judge(cnt, k):need, groups = 0, 0# 职业人数 >= i 的职业数量vsum = sum(cnt.values())for i in range(1, max(cnt) + 1):if i % 3:# 最坏的情况, 每种职业轮流取 1need += vsumelse:need += min(vsum, k - groups)# 叠加小组数量groups += vsumif k <= groups: return need# 剔除人数 <= i 的职业vsum -= cnt.get(i, 0)return -1for _ in range(int(input())):n, k = map(int, input().split())# 使用计数器cnt = Counter()for _ in range(n):a, b = map(int, input().split())cnt.update({a: b})# 职业人数 -> 职业数量cnt = Counter(cnt.values())print(judge(cnt, k))
相关文章:
蓝桥杯【第15届省赛】Python B组
这题目难度对比历届是相当炸裂的简单了…… A:穿越时空之门 【问题描述】 随着 2024 年的钟声回荡,传说中的时空之门再次敞开。这扇门是一条神秘的通道,它连接着二进制和四进制两个不同的数码领域,等待着勇者们的探索。 在二进制…...
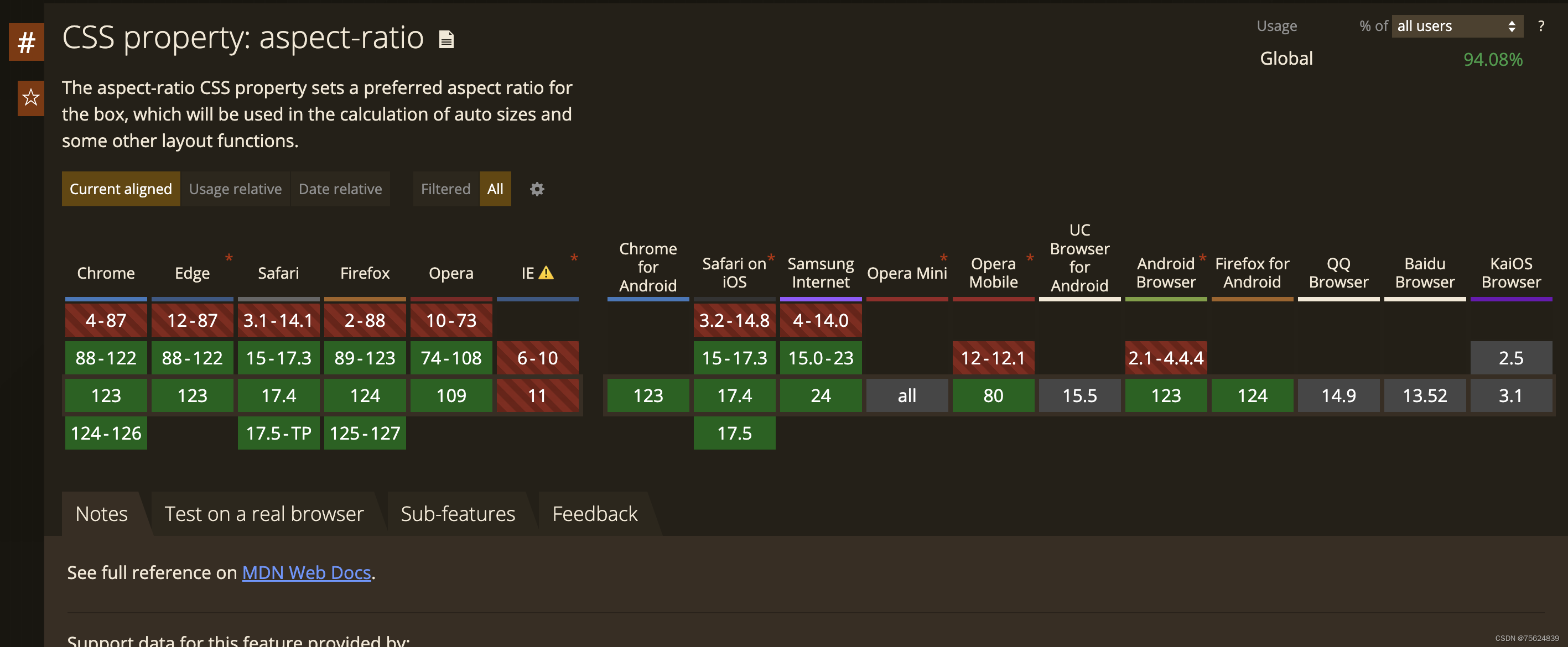
CSS aspect-ratio属性设置元素宽高比
aspect-ratio 是CSS的一个属性,用于设置元素的期望宽高比。它设置确保元素保持特定的比例,不受其内容或容器大小的影响。 语法: aspect-ratio: <ratio>;其中 <ratio> 是一个由斜杠(/)分隔的两个数字&…...

Jones矩阵符号运算
文章目录 Jones向量Jones矩阵 有关Jones矩阵、Jones向量的基本原理,可参考这个: 通过Python理解Jones矩阵,本文主要介绍sympy中提供的有关偏振光学的符号计算工具 Jones向量 Jones向量是描述光线偏振状态的重要工具,例如一个偏振…...

解决 App 自动化测试的常见痛点!
App 自动化测试中有些常见痛点问题,如果框架不能很好的处理,就可能出现元素定位超时找不到的情况,自动化也就被打断终止了。很容易打消做自动化的热情,导致从入门到放弃。比如下面的两个问题: 一是 App 启动加载时间较…...

2016NOIP普及组真题 1. 买铅笔
线上OJ: 一本通:http://ybt.ssoier.cn:8088/problem_show.php?pid1973 核心思想: 向上取整的代码 (m (n-1))/n 。(本题考点与2023年J组的第一和第二题一样) 比如需要买31支笔,每包30支,则需要…...
机器学习—数据集(二)
1可用数据集 公司内部 eg:百度 数据接口 花钱 数据集 学习阶段可用的数据集: sklearn:数据量小,方便学习kaggle:80万科学数据,真实数据,数据量大UCI:收录了360个数据集,覆盖科学、生活、经济等…...

华为S5735S核心交换配置实例
以下脚本实现创建vlan2,3,IP划分,DHCP启用,接口划分,ssh,telnet,http,远程登录启用 默认用户创建admin/admin123提示首次登录需要更改用户密码S5735产品手册更多功能配置,移步官网参考手册配置 system-viewsysname t…...

Mysql主从复制安装配置
mysql主从复制安装配置 1、基础设置准备 #操作系统: centos6.5 #mysql版本: 5.7 #两台虚拟机: node1:192.168.85.111(主) node2:192.168.85.112(从)2、安装mysql数据库 #详细安装和卸载的步骤…...

【刷题】图论——最小生成树:Prim、Kruskal【模板】
假设有n个点m条边。 Prim适用于邻接矩阵存的稠密图,时间复杂度是 O ( n 2 ) O(n^2) O(n2),可用堆优化成 O ( n l o g n ) O(nlogn) O(nlogn)。 Kruskal适用于稀疏图,n个点m条边,时间复杂度是 m l o g ( m ) mlog(m) mlog(m)。 Pr…...

使用uniapp实现小程序获取wifi并连接
Wi-Fi功能模块 App平台由 uni ext api 实现,需下载插件:uni-WiFi 链接:https://ext.dcloud.net.cn/plugin?id10337 uni ext api 需 HBuilderX 3.6.8 iOS平台获取Wi-Fi信息需要开启“Access WiFi information”能力登录苹果开发者网站&…...

回忆杀之手搓当年搓过的Transformer
整体代码 import mathimport paddle import paddle.nn as nn import paddle.nn.functional as Fclass MaskMultiHeadAttention(nn.Layer):def __init__(self, hidden_size, num_heads):super(MaskMultiHeadAttention, self).__init__()assert hidden_size % num_heads 0, &qu…...

【AR】使用深度API实现虚实遮挡
遮挡效果 本段描述摘自 https://developers.google.cn/ar/develop/depth 遮挡是深度API的应用之一。 遮挡(即准确渲染虚拟物体在现实物体后面)对于沉浸式 AR 体验至关重要。 参考下图,假设场景中有一个Andy,用户可能需要放置在包含…...

python-pytorch实现skip-gram 0.5.001
python-pytorch实现skip-gram 0.5.000 数据加载、切词准备训练数据准备模型和参数训练保存模型加载模型简单预测获取词向量画一个词向量的分布图使用词向量计算相似度参考数据加载、切词 按照链接https://blog.csdn.net/m0_60688978/article/details/137538274操作后,可以获得…...

C语言:约瑟夫环问题详解
前言 哈喽,宝子们!本期为大家带来一道C语言循环链表的经典算法题(约瑟夫环)。 目录 1.什么是约瑟夫环2.解决方案思路3.创建链表头结点4.创建循环链表5.删除链表6.完整代码实现 1.什么是约瑟夫环 据说著名历史学家Josephus有过以下…...
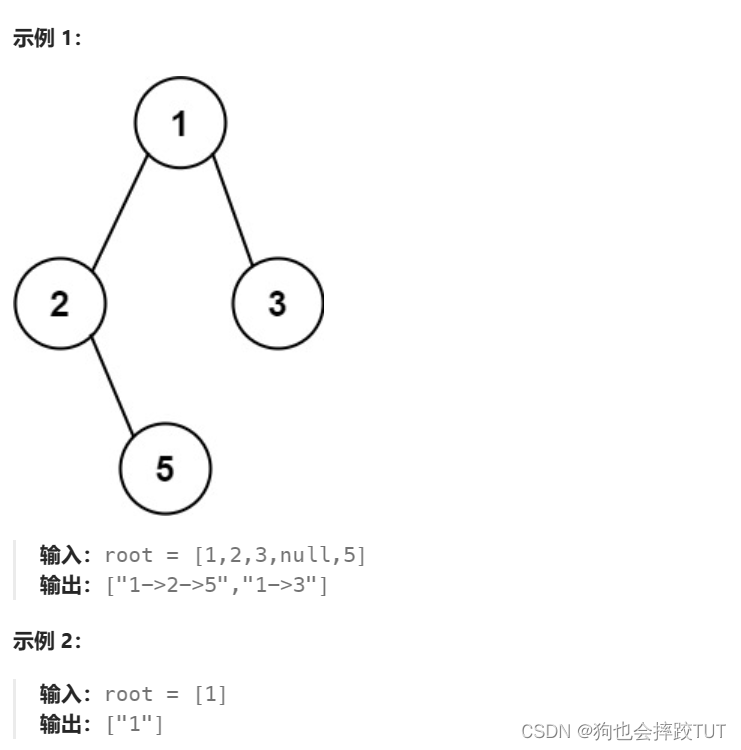
【刷题篇】回溯算法(二)
文章目录 1、求根节点到叶节点数字之和2、二叉树剪枝3、验证二叉搜索树4、二叉搜索树中第K小的元素5、二叉树的所有路径 1、求根节点到叶节点数字之和 给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表…...
Windows系统本地部署Jupyter Notebook并实现公网访问编辑笔记
文章目录 1.前言2.Jupyter Notebook的安装2.1 Jupyter Notebook下载安装2.2 Jupyter Notebook的配置2.3 Cpolar下载安装 3.Cpolar端口设置3.1 Cpolar云端设置3.2.Cpolar本地设置 4.公网访问测试5.结语 1.前言 在数据分析工作中,使用最多的无疑就是各种函数、图表、…...
Ansible 实战Shell 插件和模块工具)
自动化运维(二十七)Ansible 实战Shell 插件和模块工具
Ansible 支持多种类型的插件,这些插件可以帮助你扩展和定制 Ansible 的功能。每种插件类型都有其特定的用途和应用场景。今天我们一起学习Shell 插件和模块工具。 一、 Shell 插件 Ansible shell 插件决定了 Ansible 如何在远程系统上执行命令。这些插件非常关键&a…...

Jenkins使用-绑定域控与用户授权
一、Jenkins安装完成后,企业中使用,首先需要绑定域控以方便管理。 操作方法: 1、备份配置文件,防止域控绑定错误或授权策略选择不对,造成没办法登录,或登录后没有权限操作。 [roottest jenkins]# mkdir ba…...
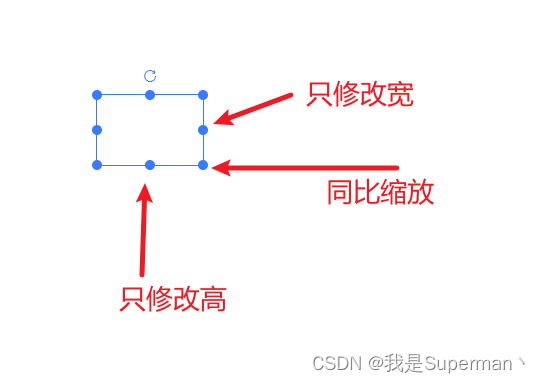
【前端】es-drager 图片同比缩放 缩放比 只修改宽 只修改高
【前端】es-drager 图片同比缩放 缩放比 ES Drager 拖拽组件 (vangleer.github.io) 核心代码 //初始宽 let width ref(108)//初始高 let height ref(72)//以下两个变量 用来区分是单独的修改宽 还是高 或者是同比 //缩放开始时的宽 let oldWidth 0 //缩放开始时的高 let o…...

蓝桥杯第十四届蓝桥杯大赛软件赛省赛C/C++ 大学 A 组题解
1.幸运数 题目链接:0幸运数 - 蓝桥云课 (lanqiao.cn) #include<bits/stdc.h> using namespace std; bool deng(string& num){int n num.size();int qian 0,hou 0;for(int i0;i<n/2;i) qian (num[i]-0);for(int in/2;i<n;i) hou (num[i]-0);r…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...
