【学习心得】神经网络知识中的符号解释②
我在上篇文章中初步介绍了一些神经网络中的符号,只有统一符号及其对应的含义才能使我自己在后续的深度学习中有着一脉相承的体系。如果对我之前的文章感兴趣可以点击链接看看哦:
【学习心得】神经网络知识中的符号解释①![]() http://t.csdnimg.cn/f6PeJ
http://t.csdnimg.cn/f6PeJ
一、神经网络简单模型
今天我以逻辑回归任务为例来介绍更多神经网络中的符号和他们对应的概念解释。先看一个超简单的神经网络模型:

这个模型对应了一个公式:
x是你输入的特征。w是权重,b是偏置,他们统称参数。我们可以将逻辑回归的模型再精细一点:
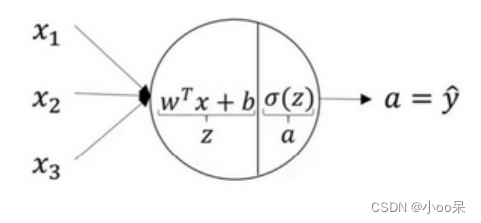
可见中间这个点,其实是有两个部分组成,第一个部分是线性部分,第二个部分是非线性部分。z是线性回归部分的输出,a是激活函数的输出。他们合在一起组成了逻辑回归的输出。可以写成如下公式:
公式中的是Sigmoid函数(激活函数的一种),L是损失函数(Loss Function)。好的介绍到这里我来个表格给大家复习一下:
| 符号 | 解释 |
| 特征值向量 | |
| 线性回归方程 | |
| Sigmoid激活函数 | |
| 损失函数 | |
| 权重向量 | |
| 偏置,偏置是一个标量在计算的时候被广播 |
二、两层神经网络
不废话,直接看图:
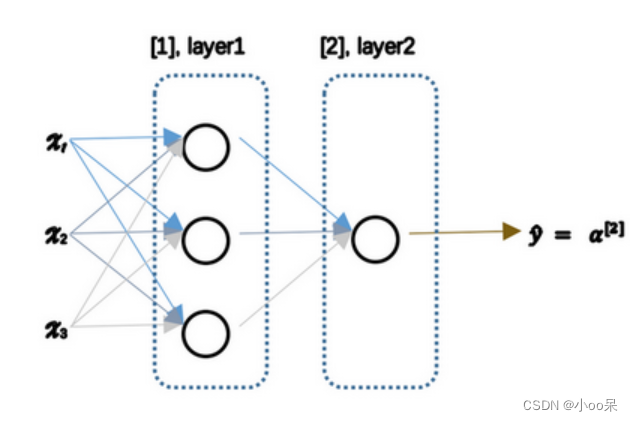
从图中可知,我们有三个输入特征他们被竖起来堆叠,这叫做神经网络的输入层。中间有两个虚线,其中处最后一个外,统称隐藏层。而最后一个虚线部分(这层只有一个节点)叫做输出层。
我们还用之前的公式和符号来表示这个神经网络模型,但稍有不同:
我们使用上角标中括号里面写数字的形式来表示第几层神经网络。这里要和之前的小括号里面写数字的形式区分开来
它表示第i个训练样本。可见上面这个公式只写出了第1层神经网络的公式。接下来我们把第二层也写出来:
和上面的第1层比较类似,我就不赘述。上面我介绍了两层神经网络的正向传播,接下来要介绍反向传播的公式:
这里面要解释的符号,就是da它是每一层逻辑回归输出的梯度,dz它是每一层线性回归输出的梯度,dW是每一层权重的梯度,db是每一层偏置的梯度。
好啦,让我再用一个表格为大家总结一下:
| 符号 | 解释 |
| 上角标中括号里面写数字,代表第m层 | |
| 偏置w的行向量形式,即 | |
| 第0层的输出,其实就是输入层的特征值向量x | |
| 第 | |
| 第 | |
| 第 | |
| 第 |
相关文章:
【学习心得】神经网络知识中的符号解释②
我在上篇文章中初步介绍了一些神经网络中的符号,只有统一符号及其对应的含义才能使我自己在后续的深度学习中有着一脉相承的体系。如果对我之前的文章感兴趣可以点击链接看看哦: 【学习心得】神经网络知识中的符号解释①http://t.csdnimg.cn/f6PeJ 一、…...

Igh related:Small Bug And Notes Record.
Write at the top My computer got some silly problem with the typing software that my Chinese IM does’t work again. So I’ll try to record the things happened in English. If any error,DM me plz. BUGs BUG1 Undefined symbol Identifier “CLOCK_MONOTONIC”…...
)
【QT入门】Qt自定义控件与样式设计之qss介绍(Qt style sheet)
往期回顾: 【QT入门】 无边框窗口设计之实现圆角窗口-CSDN博客【QT入门】 无边框窗口设计综合运用之自定义标题栏带圆角阴影的窗口-CSDN博客 【QT入门】 无边框窗口设计之综合运用,实现WPS的tab页面-CSDN博客 【QT入门】Qt自定义控件与样式设计之qss介绍…...
-第49题:字母异位词分组)
[ LeetCode ] 题刷刷(Python)-第49题:字母异位词分组
题目描述 给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。 字母异位词是由重新排列源单词的所有字母得到的一个新单词。 即将含有相同字符但排列顺序不同的字符串放入同一个组中。 示例 示例 1: 输入: strs ["eat", &qu…...

冒泡排序算法实现步骤
算法实现的过程: 1. 定义问题: - 算法是用来解决某一特定计算问题的方法步骤。例如,对于排序问题,我们需要一个算法对一组无序的整数进行排序。 2. 设计算法: - 冒泡排序是一种基础的排序算法。它的设计思路是…...

js实现webp转png/jpg
网上保存的图片是webp类型的,但是我把它嵌入flac格式的音频里后导致网页中无法播放 wps要会员,真麻烦。 完整代码: <!DOCTYPE html> <html lang"zh-CN"> <head> <meta charset"UTF-8">…...

DVWA -File Upload-通关教程-完结
DVWA -File Upload-通关教程-完结 文章目录 DVWA -File Upload-通关教程-完结页面功能LowMediumHighImpossible 页面功能 此页面的功能为选择某个图片文件点击Upload按钮上传,上传成功后得知文件上传路径为DVWA\hackable\uploads。 Low 源码审计 这段 PHP 代码…...

中介者模式:简化对象间通信的协调者
在面向对象的软件开发中,中介者模式是一种重要的行为型设计模式,用于降低多个对象间通信的复杂性。通过提供一个中心化的对象来处理不同组件之间的交互,中介者模式使得组件间不必显式引用彼此,从而使其松散耦合、更易于维护。本文…...

【Python系列】pydantic版本问题
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
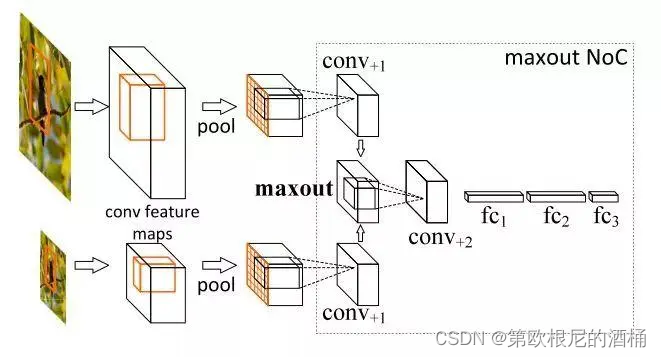
深度学习-多尺度训练的介绍与应用
一、引言 在当今快速发展的人工智能领域,多尺度训练已经成为了一种至关重要的技术,特别是在处理具有复杂结构和不同尺度特征的数据时。这种技术在许多应用中发挥着关键作用,例如图像识别、自然语言处理和视频分析等。 多尺度训练的定义 多尺…...

详解单文件组件
当你创建 Vue 单文件组件时,通常会包含三个部分:<template>、<script> 和 <style>。这三个部分分别用于定义组件的模板、逻辑和样式。让我更详细地解释一下它们的作用和用法: <template> <template> 标签用于…...

MLeaksFinder报错
1.报错:FBClassStrongLayout.mm 文件:layoutCache[currentClass] ivars; 解决:替换为layoutCache[(id)currentClass] ivars; 2.编译正常但运行时出现crash indirect_symbol_bindings[i] cur->rebinding FBRetainCycleDetector iOS15 …...

【心路历程】初次参加蓝桥杯实况
送给大家一句话: 寂静的光辉平铺的一刻,地上的每一个坎坷都被映照得灿烂。 – 史铁生 《我与地坛》 初次参加蓝桥杯有感 一点小小的震撼难评的做题过程A题 艺术与篮球问题描述解题 B 题 五子棋问题描述解题 C题 训练士兵问题描述解题 D题 团建解题 E题 …...

微信小程序全屏开屏广告
效果图 代码 <template><view><!-- 自定义头部 --><u-navbar title" " :bgColor"bgColor"><view class"u-nav-slot" slot"left"><view class"leftCon"><view class"countDown…...
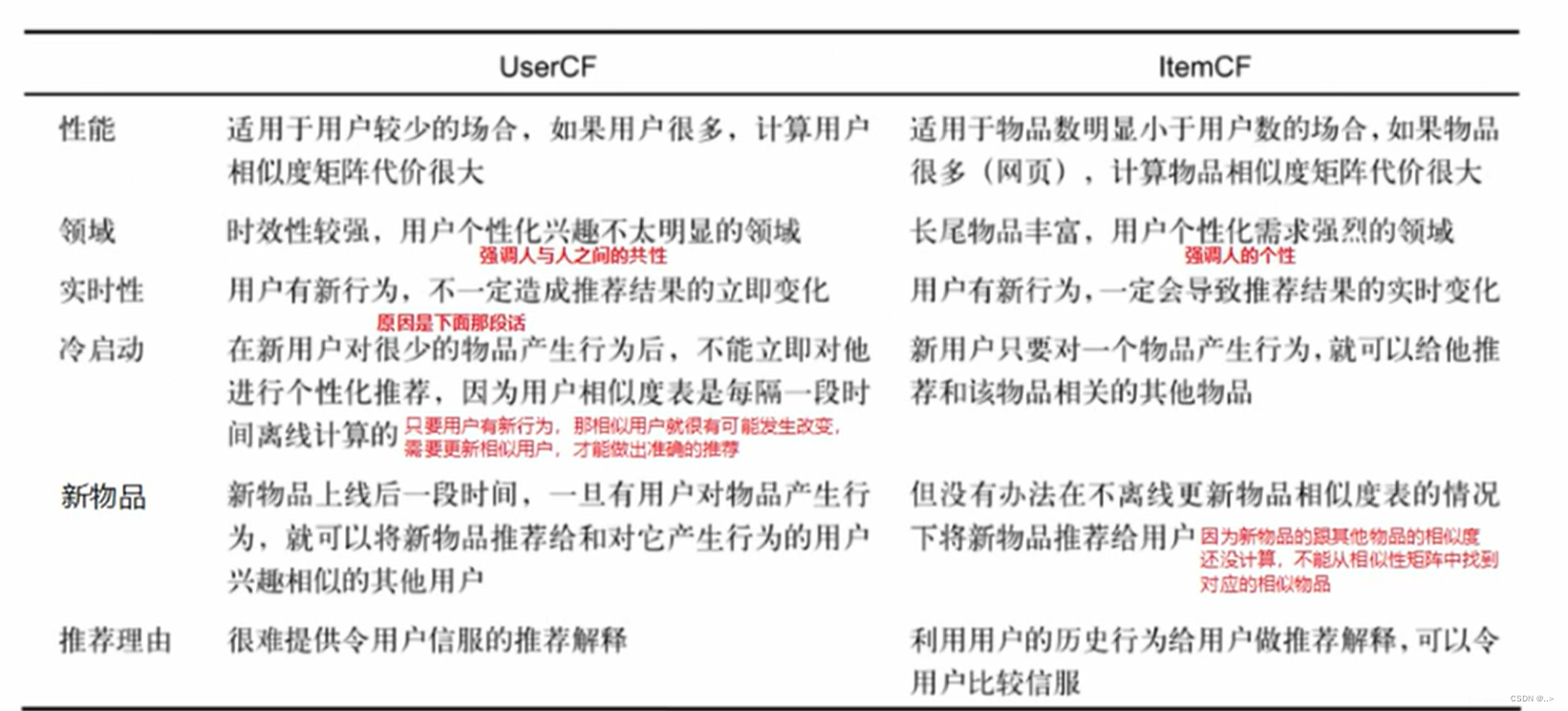
记录day1
1.早上 ①协同过滤算法 基于物品基于用户分别是如何实现的 相似度的计算方式 基于用户和基于物品的区别 实时性和新物品这里: 实时性指的是用户有新行为,这样基于物品就好,因为用户新行为了,用户矩阵不会变化,用户…...

stm32GPio的开发基础
上拉输入:高电平(弱高电平,一般默认) 下拉输入:低电平 没有上拉下拉就是处于一个不确定的状态 推挽wan输出:驱动能力比较强,推挽是因为往外推 set就是1,reset就是0 XMX就是封装的…...

DataSource
目录 1、 DataSource 1.1、 * 建立数据库连接的参数对象 1.1.1、 * 数据库url 1.1.2、 * 数据库用户名 1.1.3、 * 数据库密码 1.1.4、 * 数据库驱动名称 <...

Linux防止暴力破解密码脚本
1.认识记录linux记录安全的日志 [roottestpm ~]# cd /var/log/ [roottestpm log]# ls | grep secure secure 2.该日志的内容查看 [roottestpm log]# tail -f secure #表示ssh身份验证失败 Aug 29 23:35:03 testpm sshd[111245]: pam_unix(sshd:auth): authentication fa…...

Unity 遮罩
编辑器版本 2017.2.3f1 学习Unity的三张遮罩方式 1. Mask 遮罩方式 首先,在界面上创建2个Image,一个命名Img_Mask,大小设置 400* 400, 一个命名Img_Show,大小设置500*500。 然后,给 Img_Mask添加Mask,选择Img_Mask,点击Add Com…...

jmeter实验 模拟:从CSV数据到加密请求到解密返回数据再到跨越线程组访问解密后的数据
注意,本实验所说的加密只是模拟加密解密,您需要届时写自己的加解密算法或者引用含有加密算法的相关jar包才行. 思路: 线程组1: 1.从CSV文件读取原始数据 2.将读取到的数据用BeanShell预习处理器进行加密 3.HTTP提取器使用加密后的数据发起请求 4.使用BeanShell后置处理器…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
