每日OJ题_01背包③_力扣494. 目标和(dp+滚动数组优化)
目录
力扣494. 目标和
问题解析
解析代码
滚动数组优化代码
力扣494. 目标和
494. 目标和
难度 中等
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1 输出:1
提示:
1 <= nums.length <= 200 <= nums[i] <= 10000 <= sum(nums[i]) <= 1000-1000 <= target <= 1000
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {}
};问题解析
本题可以直接用暴搜的方法解决。但是稍微用数学知识分析⼀下,就能转化成常见的背包模型问题。
设我们最终选取的结果中,前面加 + 号的数字之和为 a ,前面加 - 号的数字之和为 b ,整个数组的总和为 sum ,于是有:
- a + b = sum
- a - b = target
上面两个式子消去 b 之后,可以得到 a = (sum + target) / 2 ,也就是说,我们仅需在 nums 数组中选择一些数,将它们凑成和为 (sum + target) / 2 即可。问题就变成了力扣416. 分割等和子集这道题。 可以用相同的分析模式,来处理这道题。
以某个位置为结尾,结合题目要求,定义一个状态表示:
dp[i][j] 表示:在前 i 个数中选,总和正好等于 j ,一共有多少种选法。
状态转移方程:
dp 状态转移方程分析方式,一般都是根据最后一步的状况,来分情况讨论:
- 不选择 nums[i] :那么我们凑成总和 j 的总方案,就要看在前 i - 1 个元素中选,凑成总和为 j 的方案数。根据状态表示,此时 dp[i][j] = dp[i - 1][j] ; 。
- 选择 nums[i] :这种情况下是有前提条件的,此时的 j 应该是大于等于 nums[i]。 因为如果这个元素都比要凑成的总和大,那选择它就没有意义。那么能够凑成总和为 j 的方案数,就要看在前 i - 1 个元素中选,能否凑成总和为 j - nums[i] 。根据 状态表示,此时 dp[i][j] = dp[i - 1][j - nums[i]] ; (j >= nums[i] )。
综上,两种情况如果存在的话,应该要累加在⼀起。因此,状态转移方程为: if(j >= nums[i - 1]) dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]] ; else dp[i][j] = dp[i - 1][j] ;(如果多加一行一列,找原数组下标要减1)
初始化:多加一行一列,方便初始化,由于需要用到上一行的数据,因此可以先把第一行初始化。 第一行表示不选择任何元素,要凑成目标和 j 。只有当目标和为 0 的时候才能做到,因此第一行仅需初始化第一个元素 dp[0][0] = 1。
填表顺序:根据状态转移方程,需要从上往下填写每一行,每一个的顺序是任意的。
返回值:根据状态表示,返回 dp[n][a] 的值。 其中 n 表示数组的大小, target 表示要凑成的目标和。
解析代码
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0, n = nums.size();;for(auto& e : nums){sum += e;}int a = (sum + target) / 2;if(a < 0 || (sum + target) % 2) // 小于0或者除不尽return 0;vector<vector<int>> dp(n + 1, vector<int>(a + 1, 0));dp[0][0] = 1;for(int i = 1; i <= n; ++i){for(int j = 0; j <= a; ++j) // 第1列用到dp[0][0]初始化{if(j >= nums[i - 1])dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i - 1]];elsedp[i][j] = dp[i - 1][j];}}return dp[n][a];}
};滚动数组优化代码
背包问题基本上都是利用滚动数组来做空间上的优化:(时间也有常数的优化)
- 利用滚动数组优化。
- 直接在原始代码上修改。
在01背包问题中,优化的结果为:
- 删掉所有的横坐标。
- 修改一下 j 的遍历顺序。
(滚动数组优化代码只需能在原代码上修改就行,不用考虑什么状态表示)
class Solution {
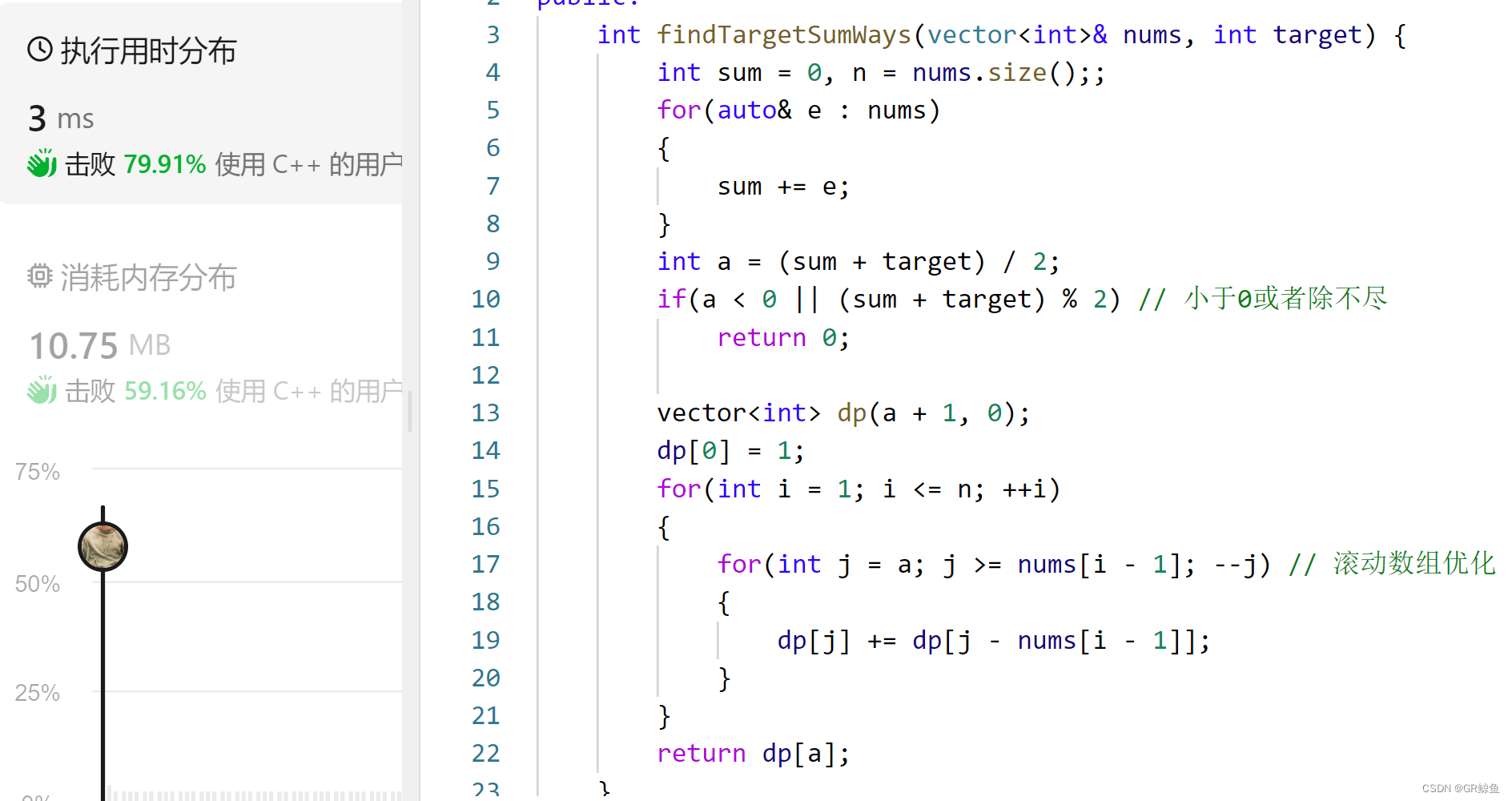
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0, n = nums.size();;for(auto& e : nums){sum += e;}int a = (sum + target) / 2;if(a < 0 || (sum + target) % 2) // 小于0或者除不尽return 0;vector<int> dp(a + 1, 0);dp[0] = 1;for(int i = 1; i <= n; ++i){for(int j = a; j >= nums[i - 1]; --j) // 滚动数组优化{dp[j] += dp[j - nums[i - 1]];}}return dp[a];}
};
相关文章:

每日OJ题_01背包③_力扣494. 目标和(dp+滚动数组优化)
目录 力扣494. 目标和 问题解析 解析代码 滚动数组优化代码 力扣494. 目标和 494. 目标和 难度 中等 给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 或 - ,然后串联起所有整数,可以构造一个 表达式 : …...

vue3+element plus图片预览点击按钮直接显示图片的预览形式
1 需求 直接上需求: 我想要直接点击下面这个“预览”按钮,然后呈现出预览图片的形式 ok,需求知道了,下面让我们来看看如何实现吧 ~ 2 实现 template部分 <el-buttontype"primary"size"small"click&qu…...
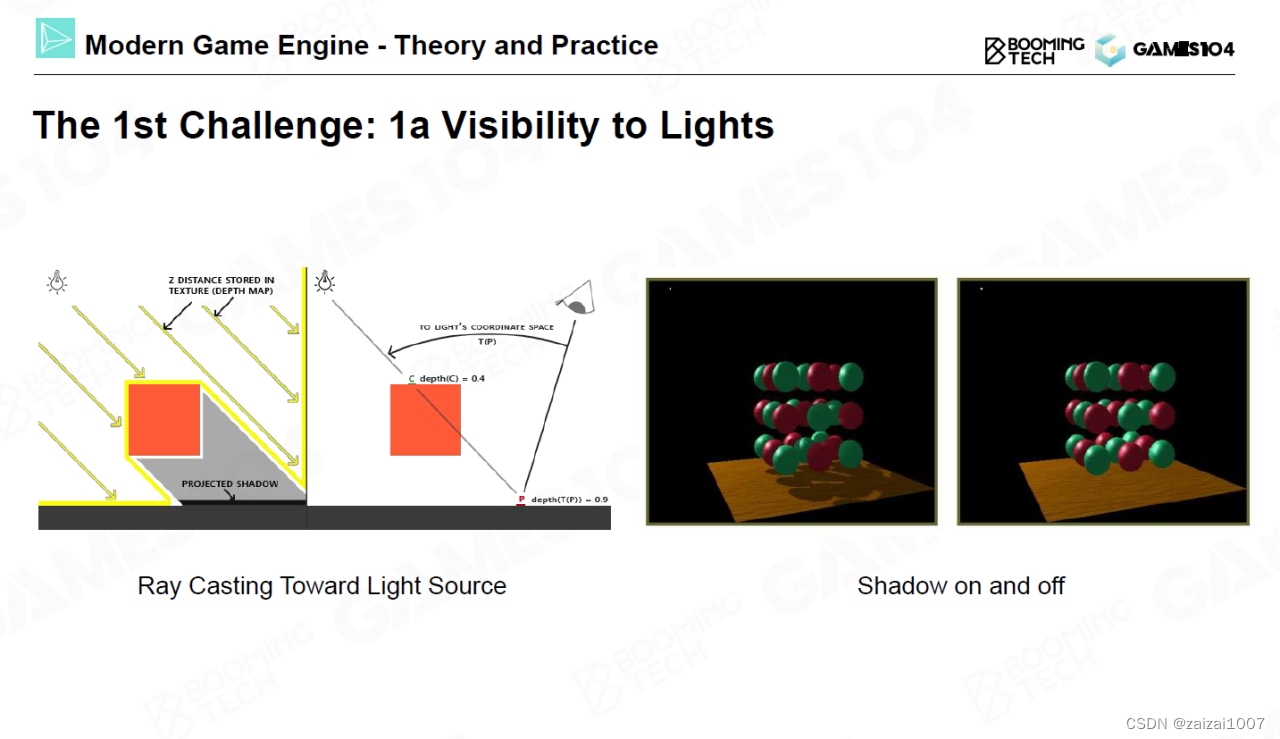
GAMS104 现代游戏引擎 2
渲染的难点可以分为一下三部分:如何计算入射光线、如何考虑材质以及如何实现全局光照。 渲染的难点之一在于阴影,或者说是光的可见性。如何做出合适的阴影效果远比想象中要难得多,在实践中往往需要通过大量的技巧才能实现符合人认知的阴影效…...
spring boot学习第十七篇:OAuth2概述及使用GitHub登录第三方网站
0. 导言 我们在浏览器上可以访问成百上千个网站,使用每个网站的服务一般都要先注册账号,那么我们为了更好地记忆,一般都会在多个网站使用相同的账号和密码进行注册。那么问题就来了,如果在你注册的网站中有某些个网站的系统设计不…...

基于springboot的电影评论网站系统源码数据库
基于springboot的电影评论网站系统源码数据库 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本文介绍了电影评论网站的开发全过程。通过分析电影评论网站管理的不足,创建了一个计算机管理电影评论网站的方案。文…...
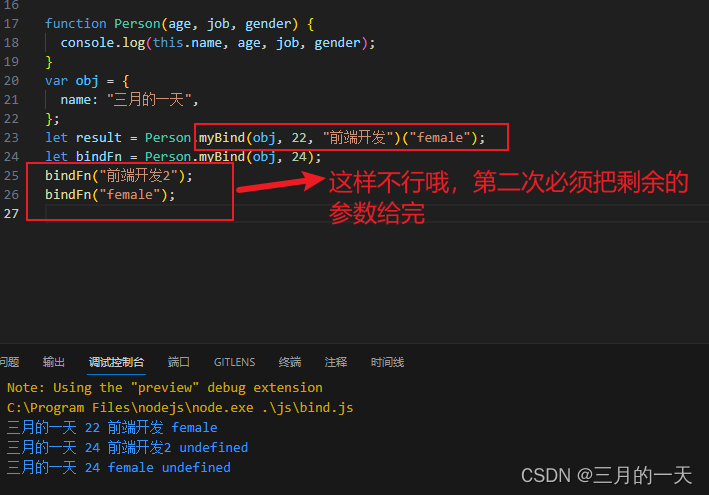
javaScript手写专题——实现instanceof/call/apply/bind/new的过程/继承方式
目录 原型链相关 手写instanceof 实现一个_instance方法,判断对象obj是否是target的实例 测试 手写new的过程 实现一个myNew方法,接收一个构造函数以及构造函数的参数,返回构造函数创建的实例对象 测试myNew方法 手写类的继承 ES6&…...

C++11 新特性:tuple 元组
std::tuple是 C11 中引入的一个非常强大的类型,它允许将多个类型不同的值,组合成单一对象。 std::tuple非常适合用于那些需要返回多个值的场景,而且它的灵活性和通用性使得其成为现代 C 编程中不可或缺的一部分。下面,我们将探讨…...
最齐全,最简单的免费SSL证书获取方法——实现HTTPS访问
一:阿里云 优势:大平台,在站长中知名度最高,提供20张免费单域名SSL证书 缺点:数量有限,并且只有单域名证书,通配符以及多域名没有免费版本。并且提供的单域名证书只有三个月的期限。 二&#…...
c语言->贪吃蛇实战技巧结合EasyX简单实现页面管理(简单实现)
✅作者简介:大家好,我是橘橙黄又青,一个想要与大家共同进步的男人😉😉 🍎个人主页:再无B~U~G-CSDN博客 1. 游戏背景 贪吃蛇是久负盛名的游戏,它也和俄罗斯⽅…...

C语言-详解内存函数
文章目录 1.memcpy使用和模拟实现1.1 memcpy函数的使用规则1.2 memcpy函数的使用1.2 模拟实现memcpy函数 2.memmove 函数的使用和模拟实现2.1 memmove 函数使用规则2.2 memmove函数的使用2.3 模拟实现memmove函数2.3.1 从后往前移2.3.2 从前往后移 2.4 算法实现2.4.1 从前往后移…...

【核心完整复现】基于目标级联法的微网群多主体分布式优化调度
1 主要内容 之前发布了华电学报的复现程序《基于目标级联法的微网群多主体分布式优化调度》,具体链接为【防骗版】基于目标级联法的微网群多主体分布式优化调度,虽然对模型及结果进行了复现,但是部分模型细节和参数并没有完全实现࿰…...
)
Mac下安装NVM,NVM安装Node(附带NPM)
1、理解NVM、node、NPM 什么是NVM? NVM: Node.js Version Manager,用来管理 node 的版本。 什么是 Node.js? Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行环境。 Node.js使用了一个事件驱动、非阻塞式I/O的模型( Node.js的特性&…...

java之变量的作用域
在java中,变量需要像其他编程语言中先定义,再使用。但并不是定义好就能用。需要对变量定义一个作用范围才能使用,这个作用范围称为作用域。 在java程序中,变量会定义在一个花括号内,花括号内的区域就是作用域。 比如…...

CentOS 7软件安装全攻略:YUM命令详解与实战
在CentOS 7中,软件安装主要依赖于其强大的包管理器——YUM(Yellowdog Updater Modified)。YUM可以自动解决软件包之间的依赖关系,使得软件的安装、更新和卸载变得简单而高效。本文将详细介绍CentOS 7中软件安装的相关命令、选项和…...
达梦关键字(如:XML,EXCHANGE,DOMAIN,link等)配置忽略
背景:在使用达梦数据库时,查询SQL中涉及XML,EXCHANGE,DOMAIN,link字段,在达梦中是关键字,SQL报关键词不能使用的错误。 解决办法: 配置达梦安装文件E:\MyJava\dmdbms\data\DAMENG\dm.ini 忽略这些关键词,…...
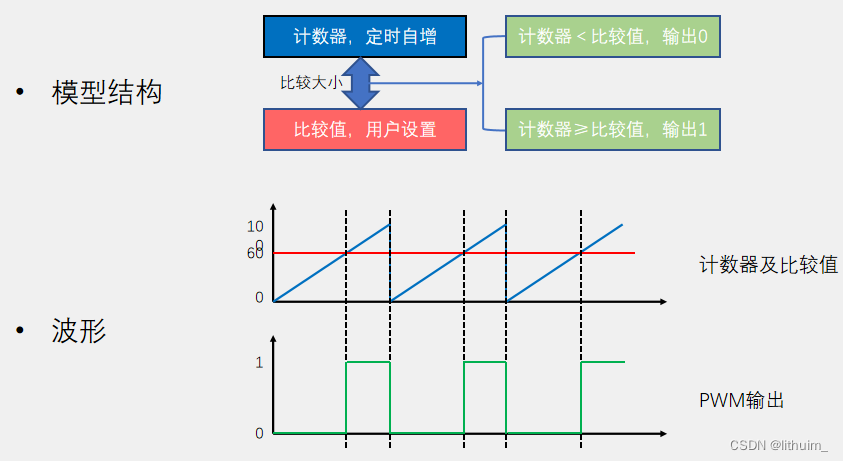
2024/4/11 直流电机调速/PWM
一、直流电机简介和PWM原理 直流电机是一种将电能转换为机械能的装置。一般的直流电机有两个电极,当电极正接时,电机正转,当电极反接时,电机反转 直流电机主要由永磁体(定子)、线圈(转子&…...

贝乐虎儿歌v6.8.0解锁高级版亲子学习儿歌
软件介绍 贝乐虎儿歌免费版app,出自乐擎网络的创意工坊,专为孩子们雕琢了一系列富含创意的动画儿歌内容。这款app通过贝乐虎兄弟的可爱形象,让孩子们在愉快的观看中接触到各种儿歌和故事。不仅如此,app还巧妙地将古诗、英语等学习…...

计算机网络技术-RIP、0SPF和BGP协议的工作原理和应用
目录 RIP (Routing Information Protocolv)路由信息协议OSPF(Open Shortest Path First) 开放式最短路径优先BGP( Border Gateway Protocol)边界网关协议 RIP (Routing Information Protocolv)路由信息协议 RIP协议 是 TCP/IP环境中开发的第一个路由选择…...

机器学习——自动驾驶
本章我们主要学习以下内容: 阅读自动驾驶论文采集数据根据论文搭建自动驾驶神经网络训练模型在仿真环境中进行自动驾驶 论文介绍 本文参考自2016年英伟达发表的论文《End to End Learning for Self-Driving Cars》 📎end2end.pdf...
VolumeManager 和 NetlinkManger)
Android 14 vold 分析(2)VolumeManager 和 NetlinkManger
3. VolumeManager::Instance() 和 VolumeManager::start() system/vold/VolumeManager.cpp 3.1 Instance()没啥好说的 非常简单 112 VolumeManager* VolumeManager::Instance() {113 if (!sInstance) sInstance new VolumeManager();114 return sInst…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...
