【muzzik 分享】3D模型平面切割

# 前言
一年一度的征稿到了,倒腾点存货,3D平面切割通常用于一些解压游戏里,例如水果忍者,切菜这些,今天我就给大家讲讲怎么实现3D切割以及其原理,帮助大家更理解3D中的 Mesh(网格),以及UV贴图和法线
由于和参赛帖另一篇文章主题相同,先自证一下这是存货
本来想等 Store 审核通过再发,但是免得大家说我抄袭就先上了
# 准备工作
了解模型
想要切割一个模型,首先要了解模型是怎么组成的,其实所有模型都是由一个个三角面组成,如下

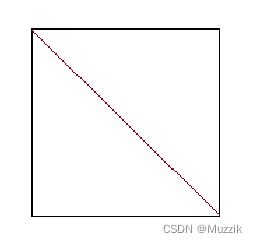
一个平面最少由两个三角形组成,而模型就是由多个三角形组成,我们要切割模型,其实就是做三角形的分割
做三角形的分割,首先我们需要一个方向,在 2D 中是一个方向向量,在 3D 中就是一个平面
创建平面对象
在 Creator3.x 版本下怎么创建这个平面对象?在 cc.geometry 中有很多几何对象类型,我们就使用其中的 cc.geometry.Plane 进行创建
const node_ui_transform =node_.getComponent(cc.UITransform) ||node_.addComponent(cc.UITransform);
const panel_ui_transform =panel_.getComponent(cc.UITransform) ||panel_.addComponent(cc.UITransform);this._plane = cc.geometry.Plane.fromNormalAndPoint(new cc.geometry.Plane(),// 法线方向(基于被切割节点坐标系,平面上方到自身的方向向量)node_ui_transform.convertToNodeSpaceAR(panel_ui_transform.convertToWorldSpaceAR(cc.Vec3.UP)).subtract(node_ui_transform.convertToNodeSpaceAR(panel_.worldPosition)).normalize(),// 平面在切割节点的本地坐标node_ui_transform.convertToNodeSpaceAR(panel_.worldPosition)
);
- node_:被切割节点
- panel_:平面节点
获取网格数据
有了用于切割时的平面对象,我们还需要 Mesh 数据,这些数据有什么?看下图
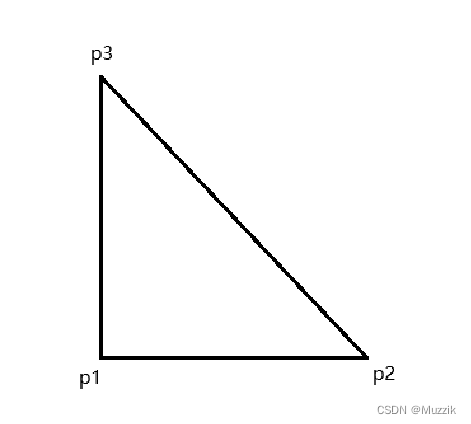
- 顶点数据:例如 [p1,p2,p3],存放所有三角形点的坐标数据
- 顶点索引:例如 [0,1,2],是顶点数据数组的下标,用来指定下标的数据组成一个三角形
怎么获取?
// 获取 cc.Mesh
this._mesh = node_.getComponent(cc.MeshRenderer)!.mesh!;/** 网格数据 */
const mesh = cc.utils.readMesh(this._mesh, 0);
注意,这里只是获取的下标为 0 的子网格,如果一个模型包含多个子网格,那么还是需要遍历获取再切割,可以通过 this._mesh.struct.primitives.length 获取子网格数量
# 开始切割
前面说了模型是由一个个三角形组成的,那么我们只需要遍历模型的网格数据针对每个和平面相交的三角形切割就行了
-
首先需要准备两个
cc.primitives.IGeometry类型的对象,用于分别存储正反面的网格数据 -
遍历需要切割的网格三角形数据,与平面相交就切割三角形后放入对应的
cc.primitives.IGeometry,不相交就不需要切割
/** 三角形点 */
const triangle_point_as = [new _mesh_slicer.point_data(),new _mesh_slicer.point_data(),new _mesh_slicer.point_data(),
];
/** 正面 */
const positive_geometry = (this._positive_mesh.geometry =this._create_geometry());
/** 反面 */
const negative_geometry = (this._negative_mesh.geometry =this._create_geometry());// 遍历三角形切割
for (let k_n = 0, len_n = geometry_.indices!.length;k_n < len_n;k_n += 3
) {/** 三角形索引 */const indices_ns = [geometry_.indices![k_n],geometry_.indices![k_n + 1],geometry_.indices![k_n + 2],];...
}
判断三角形是否与平面相交
这里我们只需要知道三角形的顶点是否在平面的正面或者反面就可以判断是否相交,
如果三个点全在一侧则肯定不相交,如果不全在一侧则一点相交 ,我们可以使用点乘 dot 判断在平面的哪一侧
// 平面的法线 dot(三角形点) - 平面距离原点距离 > 0 即为正面
positive_b = this._plane.n.dot(p) - this._plane.d > 0;
和上面说的一样,如果三角形的三个点 positive_b 一致则是全在平面的一侧不需要切割,不一致则需要切割
// 所有顶点都在同一侧
if (triangle_point_as[0].positive_b === triangle_point_as[1].positive_b &&triangle_point_as[1].positive_b === triangle_point_as[2].positive_b
) {const mesh = triangle_point_as[0].positive_b? this._positive_mesh: this._negative_mesh;// 更新旧索引triangle_point_as.forEach((v) => {this._update_old_indices(mesh, v);});// 添加点到几何数据this._add_point_to_geometry(mesh.geometry, triangle_point_as);
}
// 不在同一侧则切割三角形
else {// 顶点 0,1 在同一侧if (triangle_point_as[0].positive_b === triangle_point_as[1].positive_b) {this._slice_triangle([triangle_point_as[2],triangle_point_as[0],triangle_point_as[1],]);}// 顶点 0,2 在同一侧else if (triangle_point_as[0].positive_b === triangle_point_as[2].positive_b) {this._slice_triangle([triangle_point_as[1],triangle_point_as[2],triangle_point_as[0],]);}// 顶点 1,2 在同一侧else {this._slice_triangle([triangle_point_as[0],triangle_point_as[1],triangle_point_as[2],]);}
}
切割三角形
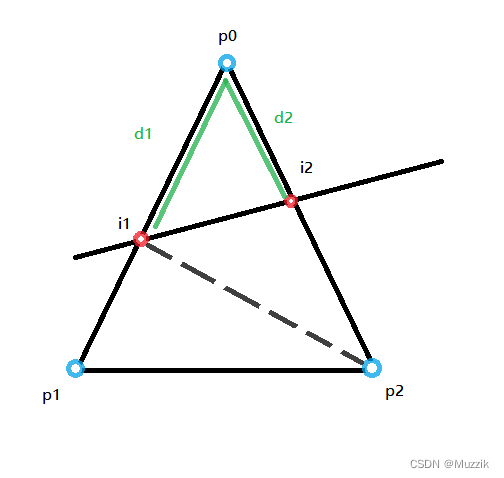
- (i1, i2) :平面
- (p0, p1, p2) :原本的三角形(逆时针为正面)
- (p0, i1, i2) :切割后的三角形
- (i1, p1, p2) : 切割后的三角形2
- (i2, i1, p2) : 切割后的三角形3
- 如果三角形三个顶点形成的线段不与平面相交,那么则不需要新建顶点
- 如果三角形线段与平面相交,则切割为三个三角形,怎么判断相交,看下面
怎么确定交点(i1, i2)?
交点也就是 i1,i2 的坐标,知道了交点才能分割三角形,以下以获取 i1 的坐标为例
- 射线公式:P = P0 + tV;
- 平面公式:A(P−P1) = 0;
这两个公式里, P 是射线上也在平面上的一个点,也就是射线和平面的交点。 P0 是射线的起点, V 是射线的方向。 t 是一个数字,当它变化时,P就会在射线上移动。 P1 是平面上的一个特定点, A 是平面的法向量。
我们将射线的公式代入到平面的公式中,就得到: A(P0 + tV - P1) = 0,求解为:t = (A * (P1 - P0))/(A * V),这里 Creator 有内置的函数,就不用自己写了
步骤为:
- 确定 i1 的坐标,从 p0 到 p1 的方向创建一条射线
cc.geometry.Ray.fromPoints(ray, p0, p1); - 计算与平面的交点距离
const distance_n = cc.geometry.intersect.rayPlane(ray, this._plane); - 获取交点坐标
ray.computeHit(point, distance_n);
这样就得到了交点,除了交点,我们还要计算法线和UV
法线和UV
法线
法线就是决定你模型的凹凸效果的,它存在于每个顶点数据中,是一个三维向量
UV
UV 就是你的模型贴图的图片坐标,它决定了你这个顶点位置展示的贴图内容在图片的什么部分,是一个二维向量
法线和UV的计算很简单,根据交点的位置使用 lerp 函数从起点和终点线段做一个插值就行了
/*** 获取线段和平面交点* @param point_as_ 线段起始和结束点* @param out_point_ 输出点* @returns*/
private _get_line_segment_and_plane_intersect(out_point_: _mesh_slicer.point_data,point_as_: _mesh_slicer.point_data[]
): _mesh_slicer.point_data {/** 射线 */const ray = cc.geometry.Ray.fromPoints(this._temp_tab.ray, point_as_[0].position_v3, point_as_[1].position_v3);/** 距离 */const distance_n = cc.geometry.intersect.rayPlane(ray, this._plane);/** 两点之间的长度 */const line_length_n = this._temp_tab.value_v3.set(point_as_[0].position_v3).subtract(point_as_[1].position_v3).length();// 计算碰撞位置ray.computeHit(out_point_.position_v3, distance_n);// 计算 uvcc.Vec2.lerp(out_point_.uv_v2, point_as_[0].uv_v2, point_as_[1].uv_v2, distance_n / line_length_n);// 计算法线cc.Vec3.lerp(out_point_.normal_v3, point_as_[0].normal_v3, point_as_[1].normal_v3, distance_n / line_length_n);return out_point_;
}/*** 获取线段和平面交点* @param point_as_ 线段起始和结束点* @param out_point_ 输出点* @returns*/private _get_line_segment_and_plane_intersect(out_point_: _mesh_slicer.point_data,point_as_: _mesh_slicer.point_data[]): _mesh_slicer.point_data {/** 射线 */const ray = cc.geometry.Ray.fromPoints(this._temp_tab.ray, point_as_[0].position_v3, point_as_[1].position_v3);/** 距离 */const distance_n = cc.geometry.intersect.rayPlane(ray, this._plane);/** 两点之间的长度 */const line_length_n = this._temp_tab.value_v3.set(point_as_[0].position_v3).subtract(point_as_[1].position_v3).length();// 计算碰撞位置ray.computeHit(out_point_.position_v3, distance_n);// 计算 uvcc.Vec2.lerp(out_point_.uv_v2, point_as_[0].uv_v2, point_as_[1].uv_v2, distance_n / line_length_n);// 计算法线cc.Vec3.lerp(out_point_.normal_v3, point_as_[0].normal_v3, point_as_[1].normal_v3, distance_n / line_length_n);return out_point_;}
/*** 切割三角形* @param point_as_ 三角形点(逆时针,首个点切割后为单三角)*/
private _slice_triangle(point_as_: _mesh_slicer.point_data[]): void {/** 单三角网格 */const mesh = point_as_[0].positive_b? this._positive_mesh: this._negative_mesh;/** 双三角网格 */const mesh2 = point_as_[0].positive_b? this._negative_mesh: this._positive_mesh;// 获取交点this._get_line_segment_and_plane_intersect(this._temp_tab.point, [point_as_[0],point_as_[1],]);this._get_line_segment_and_plane_intersect(this._temp_tab.point2, [point_as_[0],point_as_[2],]);// 添加单三角{// 更新索引this._update_new_indices(mesh, this._temp_tab.point, point_as_[1]);this._update_new_indices(mesh, this._temp_tab.point2, point_as_[2]);this._update_old_indices(mesh, point_as_[0]);// 添加三角this._add_point_to_geometry(mesh.geometry, [point_as_[0],this._temp_tab.point,this._temp_tab.point2,]);}// 添加双三角{// 更新索引this._update_new_indices(mesh2, this._temp_tab.point, point_as_[1]);this._update_new_indices(mesh2, this._temp_tab.point2, point_as_[2]);this._update_old_indices(mesh2, point_as_[1]);this._update_old_indices(mesh2, point_as_[2]);// 添加三角this._add_point_to_geometry(mesh2.geometry, [this._temp_tab.point2,this._temp_tab.point,point_as_[1],]);this._add_point_to_geometry(mesh2.geometry, [this._temp_tab.point2,point_as_[1],point_as_[2],]);}
}
简单来说就是根据交点将原本的 1 个三角形分为 3 个三角形,再根据自己正反面的位置添加到对应的正反面网格数据中并更新索引
# 生成平面

在切割结束后如果没有问题你会发现这是个空心模型,如果我们需要一个平面封住切口呢?怎么做?
这就被称为平面的 三角剖分
简单的三角剖分方案
-
求平均点,不完全支持凹多边形
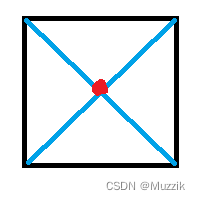
-
左右横跳,不完全支持凹多边形
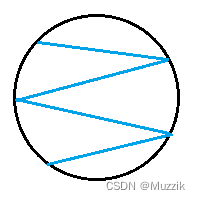
-
单点遍历,不完全支持凹多边形
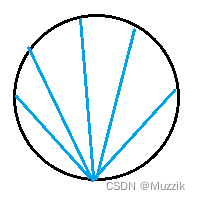
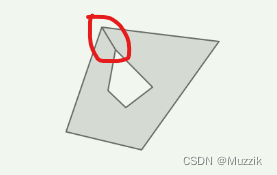
不支持凹面多边形的后果
可以看下图
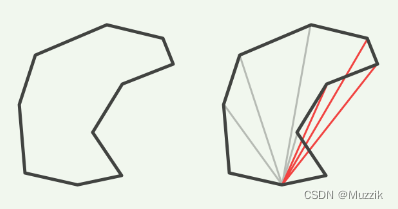
这样的话,无论是使用平均点,还是图中的单点遍历新建三角形,都会有可能出现生成的三角形错误的情况
那么如何做?步骤如下
-
记录新增的顶点坐标并排序(连线)
-
将排序后的多边形顶点分解为凸多边形
-
为所有凸多边形生成三角形
怎么判断凹凸?
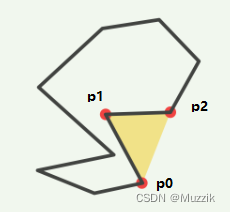
判断 p0 - p1 - p2 的夹角角度即可,这也是我们需要对新增顶点坐标排序的原因
将凹多边形分解为凸多边形
在找到凹角之后,我们只需要从 p1 的位置开始遍历至顶点,只要找到 p0 - p1 - pn 夹角不为凹角的 pn 顶点就可以分割为两个多边形,再对分割后的多边形重复执行此操作
平面带孔的情况
将排序后的两个多边形合并为一个,将内多边形的点连接到最近的一个外多边形,组合成为一个单独的多边形
但是还有一个问题,那就是单独的两个多边形可以依靠法线和碰撞检测来判断当前多边形是否在另一个内,那么多个多边形嵌套呢?
我这里想到的是使用面积判断,从大到小对多边形排序,内多边形的面积一定比外多边形小
# 源码
-
保证切割后模型原表面法线、UV 的正常
-
切口平面支持凹多边形
-
支持同时切割多个模型
-
使用共享顶点,可以节省模型内存占用
Cocos Store:https://store.cocos.com/app/detail/6118
# 其他参赛文章
原生预览调试!我给Cocos加了个新功能,原生开发者福音
相关文章:

【muzzik 分享】3D模型平面切割
# 前言 一年一度的征稿到了,倒腾点存货,3D平面切割通常用于一些解压游戏里,例如水果忍者,切菜这些,今天我就给大家讲讲怎么实现3D切割以及其原理,帮助大家更理解3D中的 Mesh(网格),以及UV贴图和…...

SCI一区 | Matlab实现OOA-TCN-BiGRU-Attention鱼鹰算法优化时间卷积双向门控循环单元融合注意力机制多变量时间序列预测
SCI一区 | Matlab实现OOA-TCN-BiGRU-Attention鱼鹰算法优化时间卷积双向门控循环单元融合注意力机制多变量时间序列预测 目录 SCI一区 | Matlab实现OOA-TCN-BiGRU-Attention鱼鹰算法优化时间卷积双向门控循环单元融合注意力机制多变量时间序列预测预测效果基本介绍模型描述程序…...

nodejs安装常用命令
安装 Node.js 后,你可以在命令行中使用以下常用命令: node:启动 Node.js 的交互式解释器,可以直接在命令行中执行 JavaScript 代码。 npm install <package-name>:安装一个 Node.js 模块,<packag…...

使用 Prometheus 在 KubeSphere 上监控 KubeEdge 边缘节点(Jetson) CPU、GPU 状态
作者:朱亚光,之江实验室工程师,云原生/开源爱好者。 KubeSphere 边缘节点的可观测性 在边缘计算场景下,KubeSphere 基于 KubeEdge 实现应用与工作负载在云端与边缘节点的统一分发与管理,解决在海量边、端设备上完成应…...
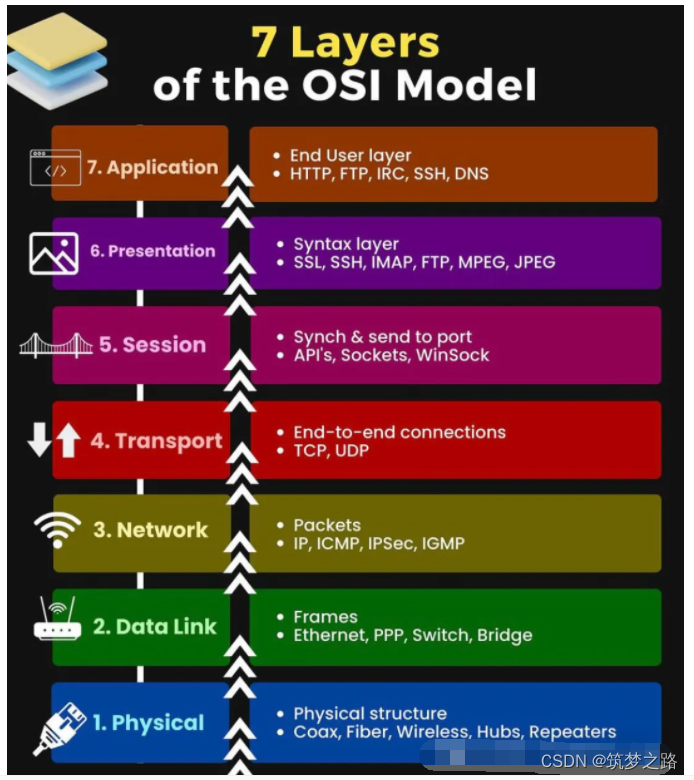
OSI七层网络模型 —— 筑梦之路
在信息技术领域,OSI七层模型是一个经典的网络通信框架,它将网络通信分为七个层次,每一层都有其独特的功能和作用。为了帮助记忆这七个层次,有一个巧妙的方法:将每个层次的英文单词首字母组合起来,形成了一句…...

状态模式:管理对象状态转换的动态策略
在软件开发中,状态模式是一种行为型设计模式,它允许一个对象在其内部状态改变时改变它的行为。这种模式把与特定状态相关的行为局部化,并且将不同状态的行为分散到对应的状态类中,使得状态和行为可以独立变化。本文将详细介绍状态…...

【论文阅读】MCTformer: 弱监督语义分割的多类令牌转换器
【论文阅读】MCTformer: 弱监督语义分割的多类令牌转换器 文章目录 【论文阅读】MCTformer: 弱监督语义分割的多类令牌转换器一、介绍二、联系工作三、方法四、实验结果 Multi-class Token Transformer for Weakly Supervised Semantic Segmentation 本文提出了一种新的基于变换…...

FMix: Enhancing Mixed Sample Data Augmentation 论文阅读
1 Abstract 近年来,混合样本数据增强(Mixed Sample Data Augmentation,MSDA)受到了越来越多的关注,出现了许多成功的变体,例如MixUp和CutMix。通过研究VAE在原始数据和增强数据上学习到的函数之间的互信息…...

2024蓝桥A组A题
艺术与篮球(蓝桥) 问题描述格式输入格式输出评测用例规模与约定解析参考程序难度等级 问题描述 格式输入 无 格式输出 一个整数 评测用例规模与约定 无 解析 模拟就好从20000101-20240413每一天计算笔画数是否大于50然后天数; 记得判断平…...

Linux journalctl命令详解
文章目录 1.介紹2.概念设置system time基本的日志查阅方法按时过滤日志(by Time)显示本次启动以来的日志(Current Boot)按Past Boots按时间窗口按感兴趣的消息筛选按unit按进程、用户、Group ID按组件路径显示内核消息按消息优先级…...
恢复MySQL!是我的条件反射,PXB开源的力量...
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...

Storm详细配置
一、认识Storm Apache Storm是个实时数据处理的“大能”,它可以实时接收、处理并转发大量数据流,就像一个高速运转的物流中心,确保数据及时、准确地到达目的地。我们要做的,就是把这个物流中心搭建起来,并且根据我们的…...

linux redis部署教程
单节点部署: 单节点部署 Redis 非常简单,只需要在一台服务器上安装 Redis 服务即可。以下是在 Linux 环境下的单节点部署步骤: 安装 Redis:打开终端,并执行以下命令来更新软件包列表并安装 Redis 服务器:…...
:如何解决餐厅等座的并发难题)
【Java】隐式锁(synchronized):如何解决餐厅等座的并发难题
当你走进一家熙熙攘攘的餐厅,准备享受一顿美味的晚餐时,你是否曾想过,这里正上演着一场场微观的线程战争?在这个场景中,每一张桌子都代表着珍贵的共享资源,而每一位顾客(线程)都在争…...
科技论文和会议录制高质量Presentation Video视频方法
一、背景 机器人领域,许多高质量的期刊和会议(如IEEE旗下的TRO,RAL,IROS,ICRA等)在你的论文收录后,需要上传一个Presentation Video材料,且对设备兼容性和视频质量有较高要求&#…...
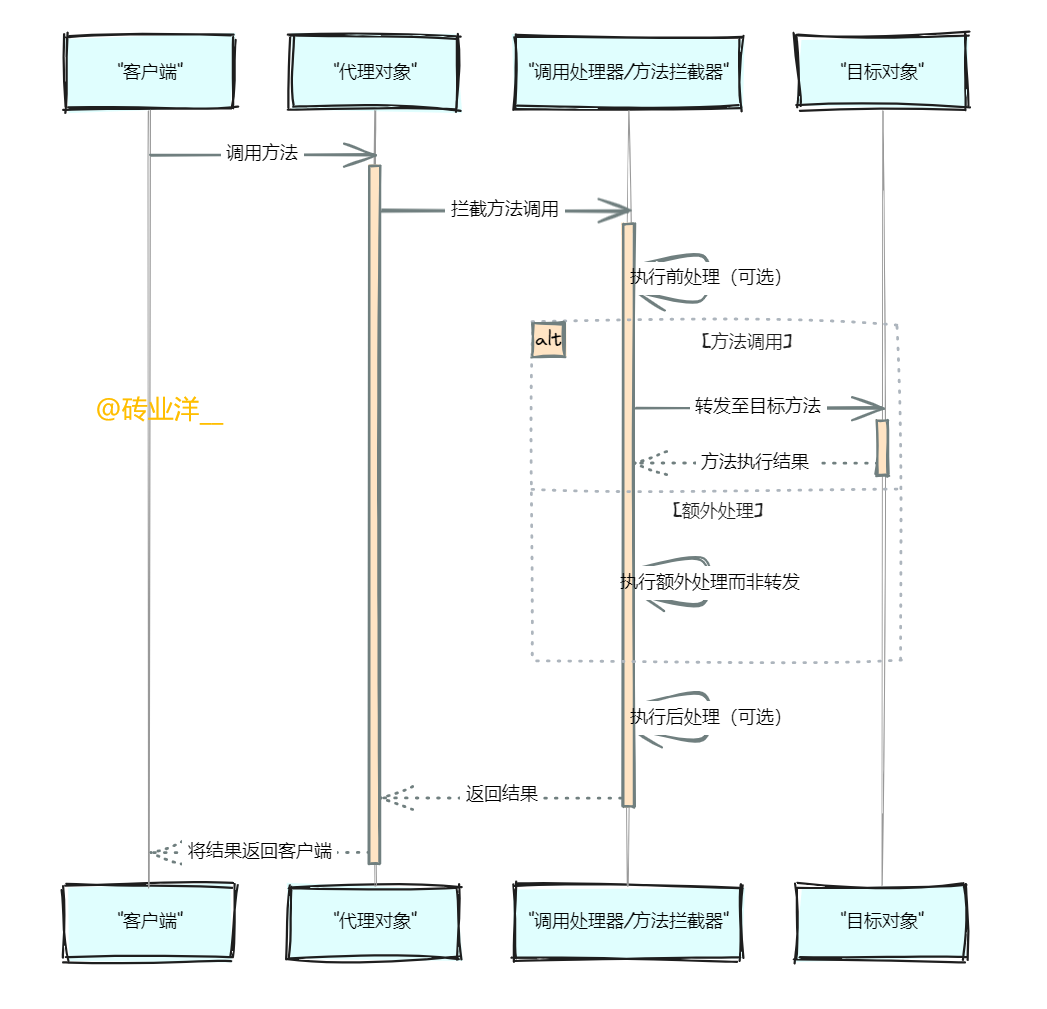
Spring高手之路17——动态代理的艺术与实践
文章目录 1. 背景2. JDK动态代理2.1 定义和演示2.2 不同方法分别代理2.3 熔断限流和日志监控 3. CGLIB动态代理3.1 定义和演示3.2 不同方法分别代理(对比JDK动态代理写法)3.3 熔断限流和日志监控(对比JDK动态代理写法) 4. 动态代理…...

如何在Unity中使用设计模式
在 Unity 环境中,设计模式是游戏开发人员遇到的常见问题的通用解决方案。将它们视为解决游戏开发中特定挑战的经过验证的模板或蓝图。以下是一些简单易懂的设计模式: 1. 单例=> 单例模式确保一个类只有一个实例,并提供对该实例的全局访问点。在 Unity 中,可以使用单例模…...
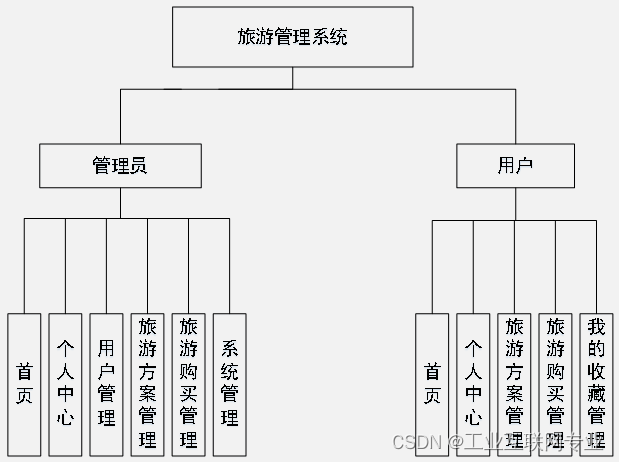
基于springboot+vue+Mysql的旅游管理系统
开发语言:Java框架:springbootJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:…...
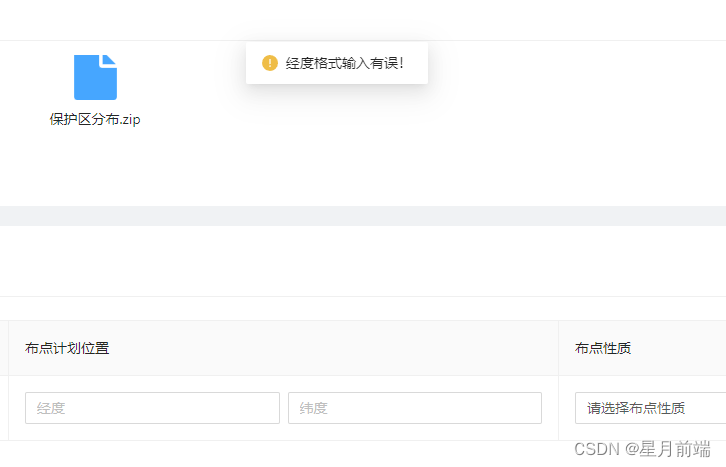
vue3+ts中判断输入的值是不是经纬度格式
vue3ts中判断输入的值是不是经纬度格式 vue代码: <template #bdjhwz"{ record }"><a-row :gutter"8" v-show"!record.editable"><a-col :span"12"><a-input placeholder"经度" v-model:v…...

python常用知识总结
文章目录 1. 常用内置函数1. ASCII码与字符相互转换 1. 常用内置函数 1. ASCII码与字符相互转换 # 用户输入字符 c input("请输入一个字符: ")# 用户输入ASCII码,并将输入的数字转为整型 a int(input("请输入一个ASCII码: "))print( c &qu…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
