头歌-机器学习 第11次实验 softmax回归
第1关:softmax回归原理
任务描述
本关任务:使用Python实现softmax函数。
相关知识
为了完成本关任务,你需要掌握:1.softmax回归原理,2.softmax函数。
softmax回归原理
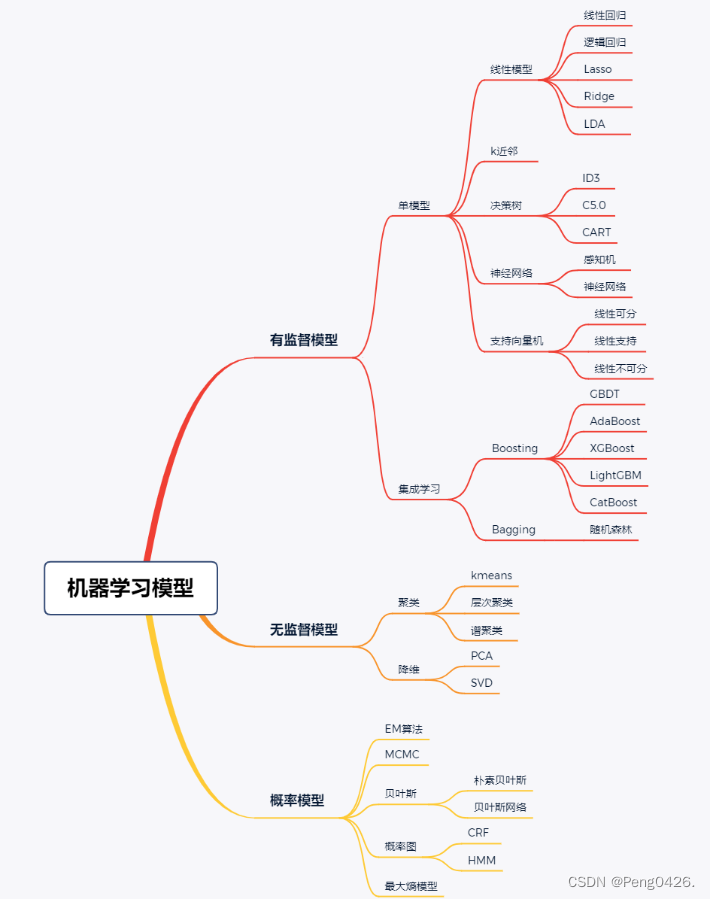
与逻辑回归一样,softmax回归同样是一个分类算法,不过它是一个多分类的算法,我们的数据有多少个特征,则有多少个输入,有多少个类别,它就有多少个输出。
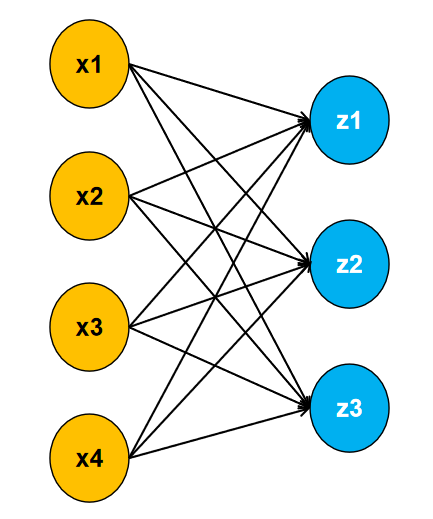
如上图,可以看出我们的数据有四个特征,三个类别。每个输入与输出都有一个权重相连接,且每个输出都有一个对应的偏置。具体公式如下:
z1=x1w11+x2w12+x3w13+x4w14+b1
z2=x1w21+x2w22+x3w23+x4w24+b2
z3=x1w31+x2w32+x3w33+x4w34+b3
输出z1,z2,z3值的大小,代表属于每个类别的可能性。如:z1=1,z2=10,z3=100表示样本预测为z3这个类别。 然而,直接将得到的输出作为判断样本属于某个类别的可能性存在不少的弊端。如,你得到一个输出为10,你可能觉得他属于这个类别的可能性很大,但另外两个输出的值都为1000,这个时候表示是这个类别的可能性反而非常小。所以,我们需要将输出统一到一个范围,如0到1之间。这个时候,如果有一个输出的值为0.9,那么你就可以非常确定,它属于这个类别了。
softmax函数
softmax函数公式如下:
y^i=∑i=1cexp(zi)exp((zi))
其中,i表示第i个类别,c为总类别数。由公式可知:
0≤y^≤0
i=1∑cy^=1
这样就可以将输出的值转换到0到1之间,且总和为1。每个类别对应的输出值可以当做样本为这个类别的概率。对于单个样本,假如一共有0,1,2三个类别,对应的输出为[0.2,0.3,0.5]则最后判断为2这个类别。
编程要求
根据提示,在右侧编辑器补充Python代码,实现softmax函数,底层代码会调用你实现的softmax函数来进行测试。
测试说明
程序会调用你实现的方法对随机生成的数据进行测试,若结果正确则视为通关,否则输出使用你方法后返回的数据。
#encoding=utf8
import numpy as npdef softmax(x):'''input:x(ndarray):输入数据,shape=(m,n)output:y(ndarray):经过softmax函数后的输出shape=(m,n)'''# 确保x是一个二维数组assert len(x.shape) == 2# 对每一行求最大值row_max = np.max(x, axis=1)# 对每个元素减去所在行的最大值x -= row_max.reshape((-1, 1))# 计算指数函数exp_x = np.exp(x)# 对每一行求和row_sum = np.sum(exp_x, axis=1)# 除以所在行的总和y = exp_x / row_sum.reshape((-1, 1))return y第2关:softmax回归训练流程
任务描述
本关任务:使用python实现softmax回归算法,使用已知鸢尾花数据对模型进行训练,并对未知鸢尾花数据进行预测。
相关知识
为了完成本关任务,你需要掌握:1.softmax回归模型,2.softmax回归训练流程。
softmax回归模型
与逻辑回归一样,我们先对数据进行向量化:
X=(x0,x1,...,xn)
其中,x0等于1。且X形状为m行n+1列,m为样本个数,n为特征个数。
W=(w1,...,wc)
W形状为n+1行c列,c为总类别个数。
Z=XW
Z形状为m行c列。
Y^=softmax(Z)
同样的,Y^的形状为m行c列。第i行代表第i个样本为每个类别的概率。
对于每个样本,我们将其判定为输出中最大值对应的类别。
softmax回归训练流程
softmax回归训练流程同逻辑回归一样,首先得构造一个损失函数,再利用梯度下降方法最小化损失函数,从而达到更新参数的目的。具体流程如下:
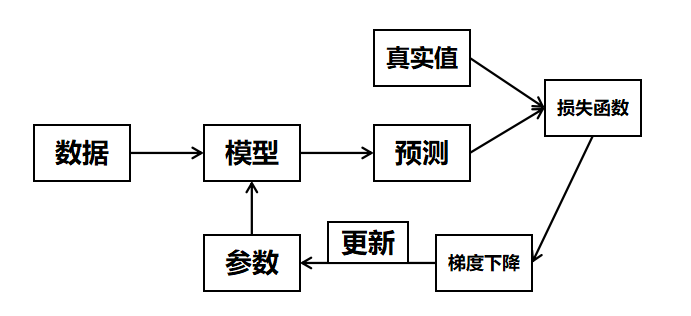
关于梯度下降详细内容请点击查看
softmax回归使用的损失函数为交叉熵损失函数,公式如下:
loss=m1i=1∑m−yilogy^i
其中,yi为onehot后的标签,y^i为预测值。同样的我们可以求得损失函数对参数的梯度为:
∂w∂loss=(y^−y)x
于是,在softmax回归中的梯度下降公式如下:
W=W−ηX.T(Y^−Y)
编程要求
根据提示,在右侧编辑器补充代码,实现softmax回归算法。
测试说明
程序会调用你实现的方法对模型进行训练,并对未知鸢尾花数据进行预测,正确率大于0.95则视为通关。
import numpy as np
from sklearn.preprocessing import OneHotEncoderdef softmax(x):'''input:x(ndarray):输入数据output:y(ndarray):经过softmax函数后的输出'''#********* Begin *********## 确保x是一个二维数组assert len(x.shape) == 2# 对每一行求最大值row_max = np.max(x, axis=1)# 对每个元素减去所在行的最大值x -= row_max.reshape((-1, 1))# 计算指数函数exp_x = np.exp(x)# 对每一行求和row_sum = np.sum(exp_x, axis=1)# 除以所在行的总和y = exp_x / row_sum.reshape((-1, 1))#********* End *********#return ydef softmax_reg(train_data,train_label,test_data,lr,max_iter):'''input:train_data(ndarray):训练数据train_label(ndarray):训练标签test_data(ndarray):测试数据lr(float):梯度下降中的学习率参数max_iter(int):训练轮数output:predict(ndarray):预测结果'''#********* Begin *********##将x0加入训练数据m,n = train_data.shapetrain_data = np.insert(train_data, 0, values=np.ones(m), axis=1)#转换为onehot标签enc = OneHotEncoder()train_label = enc.fit_transform(train_label.reshape(-1, 1)).toarray()#对w,z,y初始化w = np.zeros((n+1, train_label.shape[1]))z = np.dot(train_data, w)y = softmax(z)#利用梯度下降对模型进行训练for i in range(max_iter):# 计算梯度gradient = np.dot(train_data.T, (y - train_label))# 更新权重w -= lr * gradient# 重新计算z和yz = np.dot(train_data, w)y = softmax(z)#将x0加入测试数据m_test,n_test = test_data.shapetest_data = np.insert(test_data, 0, values=np.ones(m_test), axis=1)#进行预测predict = np.argmax(np.dot(test_data, w), axis=1)#********* End *********#return predict第3关:sklearn中的softmax回归
任务描述
本关任务:使用sklearn中的LogisticRegression类完成红酒分类任务。
相关知识
为了完成本关任务,你需要掌握如何使用sklearn提供的LogisticRegression类。
数据集介绍
数据集为一份红酒数据,一共有178个样本,每个样本有13个特征,3个类别,你需要自己根据这13个特征对红酒进行分类,部分数据如下图:

数据获取代码:
import pandas as pddata_frame = pd.read_csv('./step3/dataset.csv', header=0)
LogisticRegression
LogisticRegression中将参数multi_class设为"multinomial"则表示使用softmax回归方法。 LogisticRegression的构造函数中有三个常用的参数可以设置:
solver:{'newton-cg' , 'lbfgs', 'sag', 'saga'}, 分别为几种优化算法。C:正则化系数的倒数,默认为1.0,越小代表正则化越强。max_iter:最大训练轮数,默认为100。
和 sklearn 中其他分类器一样,LogisticRegression类中的fit函数用于训练模型,fit函数有两个向量输入:
X:大小为 [样本数量,特征数量] 的ndarray,存放训练样本Y:值为整型,大小为 [样本数量] 的ndarray,存放训练样本的分类标签
LogisticRegression类中的predict函数用于预测,返回预测标签,predict函数有一个向量输入:
X:大小为[样本数量,特征数量]的ndarray,存放预测样本
LogisticRegression的使用代码如下:
softmax_reg = LogisticRegression(multi_class="multinomial")softmax_reg.fit(X_train, Y_train)result = softmax_reg.predict(X_test)
编程要求
根据提示,在右侧编辑器补充代码,利用sklearn实现softmax回归。
测试说明
程序会调用你实现的方法对红酒数据进行分类,正确率大于0.95则视为通关。
#encoding=utf8
from sklearn.linear_model import LogisticRegression
def softmax_reg(train_data,train_label,test_data):'''input:train_data(ndarray):训练数据train_label(ndarray):训练标签test_data(ndarray):测试数据output:predict(ndarray):预测结果'''#********* Begin *********#clf = LogisticRegression(C=0.99,solver='lbfgs',multi_class='multinomial',max_iter=200)clf.fit(train_data,train_label)predict = clf.predict(test_data)#********* End *********#return predict相关文章:

头歌-机器学习 第11次实验 softmax回归
第1关:softmax回归原理 任务描述 本关任务:使用Python实现softmax函数。 相关知识 为了完成本关任务,你需要掌握:1.softmax回归原理,2.softmax函数。 softmax回归原理 与逻辑回归一样,softmax回归同样…...
Qt for MCUs 2.7正式发布
本文翻译自:Qt for MCUs 2.7 released 原文作者:Qt Group高级产品经理Yoann Lopes 翻译:Macsen Wang Qt for MCUs的新版本已发布,为Qt Quick Ultralite引擎带来了新功能,增加了更多MCU平台的支持,并且我们…...

共享IP和独享IP如何选择,两者有何区别?
有跨境用户在选择共享IP和独享IP时会有疑问,不知道该如何进行选择,共享IP和独享IP各有其特点和应用场景,选择哪种方式主要取决于具体需求和预算。以下是对两者的详细比较: 首先两者的主要区别在于使用方式和安全性:共…...

文心一言VSchatGPT4
文心一言和GPT-4各有优势,具体表现在不同的测试场景下。 在某些测试场景中心一言的表现优于GPT-4,例如在故事的完整度和情节吸引力方面,文心一言表现得更加符合指令,情节更吸引人。这可能得益于其模型在训练时对中文语境的深入理…...
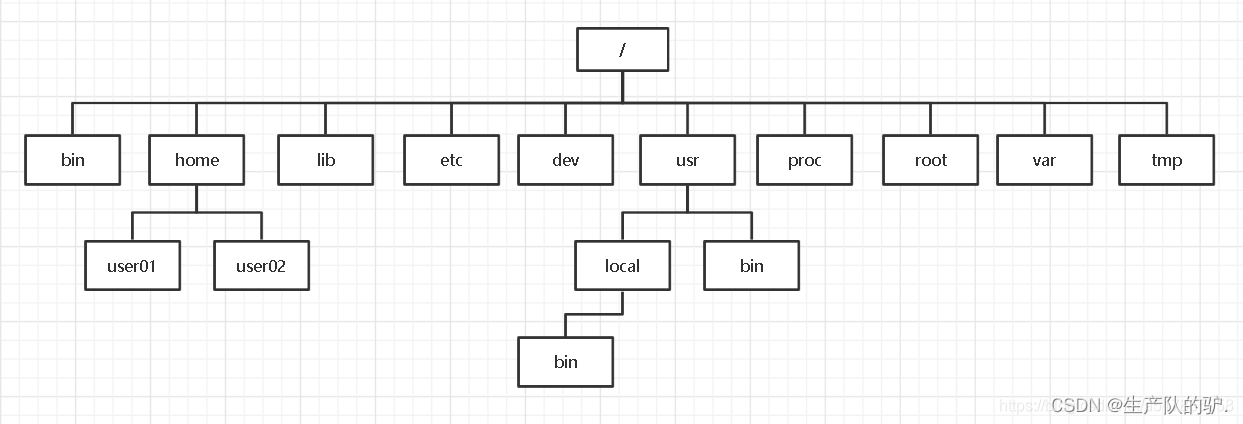
Linux 目录结构与基础查看命令
介绍 目录结构如下 /bin:存放着用户最经常使用的二进制可执行命令,如cp、ls、cat等。这些命令是系统管理员和普通用户进行日常操作所必需的。 /boot:存放启动系统使用的一些核心文件,如引导加载器(bootstrap loader…...
【matlab】如何解决打开缓慢问题(如何让matlab在十几秒内打开)
【matlab】如何解决打开缓慢问题(如何让matlab在十几秒内打开) 找到我们解压缩时Crack中的license_standalone.lic文件,将其拷贝 在安装matlab的路径下新建一个文件,粘贴上面的license_standalone.lic文件 在桌面鼠标移动到matl…...

【stata】求滚动波动情况
0.计算对象 计算 t t t、 t 1 t1 t1、 t 2 t2 t2 这三起滚动波动情况 V o l i , t l n ( ∑ n t n t 2 ( g n − g ˉ ) 2 3 ) Vol_{i,t} ln(\sqrt{\frac{\sum_{nt}^{nt2}(g_{n}-\bar{g})^2}{3}}) Voli,tln(3∑ntnt2(gn−gˉ)2 ) e . g e.g e.g: 假设 200…...
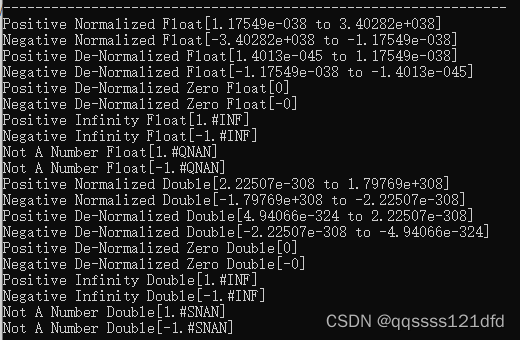
The C programming language (second edition,KR) exercise(CHAPTER 2)
E x c e r c i s e 2 − 1 Excercise\quad 2-1 Excercise2−1:输出结果如图1和图2所示,这道练习题需要文章1和文章2的知识。 #include <stdio.h> #include <limits.h>float getFloat(char sign, unsigned char exp, unsigned mantissa); do…...

rust实现循环链表
作为一个计算机技术专家,针对你的问题,我将首先解释如何使用Rust语言实现循环链表,并提供相应的代码示例。然后,我将解释一个可能的报错问题及其解决方法。 循环链表的实现 在Rust中实现循环链表,首先需要定义链表节…...

2. Spring的创建和Bean的存取
经过前面的学习我们已经大体明白了 IOC 思想以及它的实现方式 DI ,本节要讲的是如何Spring框架实现实现DI。 本节目标: Spring(Core) 项目创建将对象存储到 Spring 中将对象(bean)从 Spring 中取出 1. 创建 Spring 项目 与开篇演示的 Spring Boot 项目不…...
策略模式【行为模式C++】
1.概述 策略模式是一种行为设计模式, 它能让你定义一系列算法, 并将每种算法分别放入独立的类中, 以使算法的对象能够相互替换。 策略模式通常应用于需要多种算法进行操作的场景,如排序、搜索、数据压缩等。在这些情况下&#x…...
)
php中session相关知识(目前了解部分)
#记录学习知识 一.ini_set() 在PHP中,ini_set() 函数用于在脚本运行时设置指定的配置选项的值。这些配置选项可以是PHP的核心设置,例如文件上传的最大大小、脚本的最大执行时间、错误报告级别等。使用 ini_set() 可以临时改变PHP.ini文件中的设置&am…...

从零实现诗词GPT大模型:GPT是怎么生成内容的?
专栏规划: https://qibin.blog.csdn.net/article/details/137728228 再开始编写GPT之前,我们得对GPT是怎么生成内容的有一个大致的了解。目前的神经网络我们大多都可以看成是一个黑盒,即我们把数据输送给网络后,网络给我我们输出,我们可以不用关心这个黑盒里到底是怎么实现…...

8路HDMI+8路AV高清视频流媒体编码器JR-3218HD
产品简介: JR-3218HD高清音视频编码产品支持8路高清HDMI音视频采集功能,8路AV视频采集功能,8路3.5MM独独立音频接口采集功能。编码输出双码流H.264格式,音频MP3/AAC格式。编码码率可调,画面质量可控制。支持HTTP/RTSP…...

LangChain入门:14.LLMChain:最简单的链的使用
摘要 本文将介绍LangChain库中LLMChain工具的使用方法。LLMChain将提示模板、语言模型(LLM)和输出解析器整合在一起,形成一个连贯的处理链,简化了与语言模型的交互过程。我们将探讨LLMChain的技术特点、应用场景以及它解决的问题…...
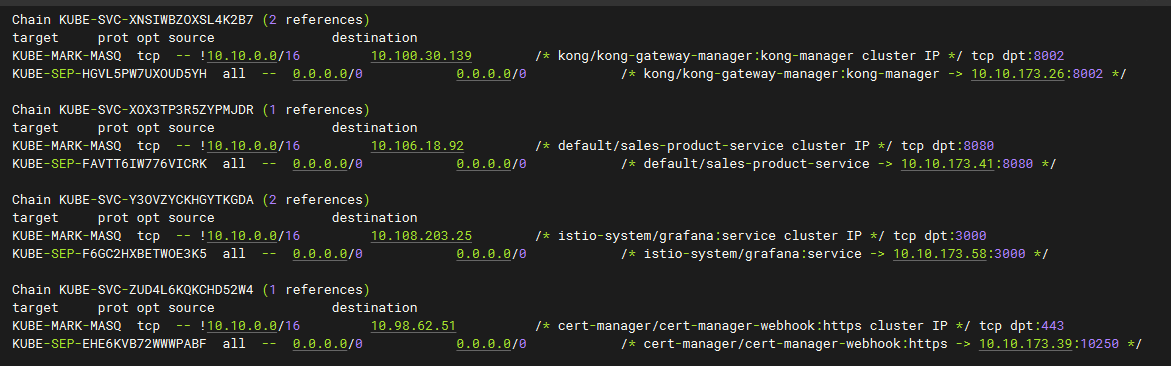
深入理解k8s kube-proxy
1、概述 我觉得只要大家知道kube-proxy是用来配置网络规则的而不是转发流量的,真正的流量由iptables/ipvs来转发就可以了。 网络是k8s的一个关键部分。理解k8s中网络组件如何工作可以帮助更好的设计和配置我们的应用。 kube-proxy就是K8s网络的核心组件。它把我们…...
Spark-机器学习(1)什么是机器学习与MLlib算法库的认识
从这一系列开始,我会带着大家一起了解我们的机器学习,了解我们spark机器学习中的MLIib算法库,知道它大概的模型,熟悉并认识它。同时,本篇文章为个人spark免费专栏的系列文章,有兴趣的可以收藏关注一下&…...

java的正则表达式校验,包含了中国几乎所有运营商手机号码的校验格式
时间2024年4月14日22:25:00 代码 String PHONE_REGEX "^1([38][0-9]|4[579]|5[0-3,5-9]|6[6]|7[0135678]|9[89])\\d{8}$";解释 这个Java代码段定义了一个常量 PHONE_REGEX,它包含了一个正则表达式,用于匹配中国大陆的手机号码。下面是对这…...
C#简单工厂模式的实现
using System.Diagnostics.Metrics; using System.Runtime.InteropServices; using static 手写工厂模式.Program;namespace 手写工厂模式 {internal class Program{public interface eats {void eat();}//定义了一个接口public class rice : eats{public void eat() {Console.…...
)
.NET 设计模式—观察者模式(Observer Pattern)
简介 在.NET中,观察者模式是一种设计模式,它允许对象之间进行一对多的依赖关系。当一个对象的状态发生变化时,所有依赖于它的对象都会收到通知并自动更新。这种模式在事件驱动的设计中非常常见。 在.NET中实现观察者模式,通常涉…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
