数据结构与算法——20.B-树
这篇文章我们来讲解一下数据结构中非常重要的B-树。
目录
1.B树的相关介绍
1.1、B树的介绍
1.2、B树的特点
2.B树的节点类
3.小结
1.B树的相关介绍
1.1、B树的介绍
在介绍B树之前,我们回顾一下我们学的树。
首先是二叉树,这个不用多说,然后为了查找的效率,我们提出了搜索二叉树(或者称为二叉搜索树),就是节点类加个key值,然后左边小右边大的那个。然后为了避免极端情况的出现,就是二叉搜索树节点集中在一侧的情况,我们提出了平衡二叉树,就是带自旋的,可以左旋或者右旋的,高度差小于1的那种,平衡二叉树里面有AVL树和红黑树两种实现方式,注意,平衡二叉树是在二叉搜索树的基础上提出的,所以平衡二叉树也叫平衡二叉搜索树。
下面介绍一下B树。
B-树是一种自平衡的多路查找树,注意: B树就是B-树,"-"是个连字符号,不是减号 。
在大多数的平衡查找树(Self-balancing search trees),比如 AVL树 和红黑树,都假设所有的数据放在主存当中。那为什么要使用 B-树呢(或者说为啥要有 B-树呢)?要解释清楚这一点,我们假设我们的数据量达到了亿级别,主存当中根本存储不下,我们只能以块的形式从磁盘读取数据,与主存的访问时间相比,磁盘的 I/O 操作相当耗时,而提出 B-树的主要目的就是减少磁盘的 I/O 操作。
大多数平衡树的操作(查找、插入、删除,最大值、最小值等等)需要 O(ℎ)次磁盘访问操作,其中 ℎ 是树的高度。但是对于 B-树 而言,树的高度将不再是log(n)(n为数中节点的个数),而是一个我们可控的高度 ℎ (通过调整 B-树中结点所包含的键【你也可以叫做数据库中的索引,本质上就是在磁盘上的一个位置信息】的数目,使得 B-树的高度保持一个较小的值)。一般而言,B-树的结点所包含的键的数目和磁盘块大小一样,从数个到数千个不等。由于B-树的高度 h 可控(一般远小于log(n)),所以与 AVL 树和红黑树相比,B-树的磁盘访问时间将极大地降低。
我们之前谈过红黑树与AVL树相比较,红黑树更好一些,这里我们将红黑树与B-树进行比较,并以一个例子对上面一段的内容进行解释。
假设我们现在有 838,8608 条记录,对于红黑树而言,树的高度 ℎ=log(838,8608)=23 ,也就是说树的高度为23,也就是说如果要查找到叶子结点需要 23 次磁盘 I/O 操作;但是 B-树,情况就不同了,假设每一个结点可以包含 8 个键(当然真实情况下没有这么平均,有的结点包含的键可能比8多一些,有些比 8 少一些),那么整颗树的高度将最多 8 ( log8(838,8608)=7.8 ) 层,也就意味着磁盘查找一个叶子结点上的键的磁盘访问时间只有 8 次,这就是 B-树提出来的原因所在。
1.2、B树的特点
下面讲一下B树的特点
在讲B树的特点之前,我们先来了解几个概念
度:degree 指树中节点的孩子数
阶:order 指所有节点中孩子数最大值
B树的特点:
- 每个节点最多有m个孩子,其中m称为B-树的阶;(孩子数目的上限)
- 除根节点和叶子节点外,其他节点至少有 ceil(m/2) (阶数除以2向上取整)个孩子,就是说B树中节点最大有m个孩子即阶个孩子,至少有 m/2(向上取整) 个孩子;(孩子数目的下限)
- 若根节点不是叶子节点,则至少有两个孩子;(根节点孩子数的下限)
- 所有叶子节点都在同一层;(B树是否平衡的前提条件)
- 每个非叶子节点由 n 个关键字(就是n个关键值,参考二叉搜索树中的关键值)和 n+1 个指针(就是n+1个孩子)组成,其中 ceil(m/2)-1 <= n <= m-1;
- 关键字按非降序排列(就是升序排列,和二叉树搜索相同),即节点中的第 i 个关键字大于等于第 i-1 个关键字;
- 指针P[ i ] 指向关键字值位于第 i 个关键字和第 i+1 个关键字之间的子树;
这些特性都要理解。看一下一个B树的实例:
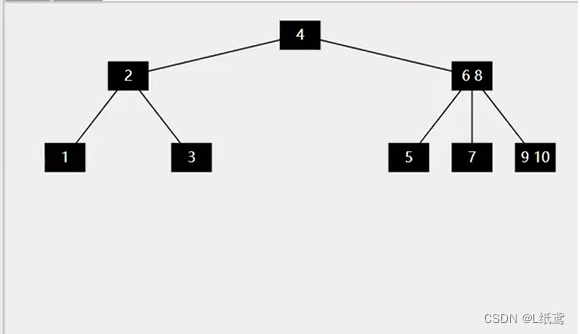
2.B树的节点类
下面,我们来看一下B树的具体实现吧
package Tree;import java.util.Arrays;public class L5_BTree {//B数的节点类static class Node{int[] keys; //关键字,即关键值,排序用的Node[] children; //孩子,存孩子用的节点类数组int keyNumber; //有效关键字数目(就是真正存了几个关键字)boolean leaf = true; //是否是叶子节点int t; //最小度数(最小孩子数)//构造函数public Node(int t) { // t >= 2this.t = t;//手动设置最小孩子数this.children = new Node[2 * t];//最大孩子数是最小孩子数的二倍this.keys = new int[2 * t -1];//关键字的最大数量 是 最大孩子数-1}@Overridepublic String toString() {return Arrays.toString(Arrays.copyOfRange(keys,0,keyNumber));}//多路查找,就是我给你一个关键值,你返回这个关键值对应的节点Node get(int key){int i = 0; //设置个变量i,方便用来循环遍历while (i < keyNumber){ //节点中有关键字if (keys[i] == key){ //如果节点中的关键字 等于 我给出的关键字,那就返回这个关键字对应的节点return this;}if (keys[i] > key){ //如果关键字中的最小值都比给出的大,那就直接退出这个节点的循环了break;}i++; //变量i自增}//执行到这里,就是说当前节点的关键字一定比给出的大,或者说,超出索引了,即keys[i]>key 或 i == keyNumberif (leaf){ //如果是叶子节点,那就肯定没有孩子了return null;}//这种情况就是 i == keyNumber 了,就找这个节点所对应的孩子了(孩子数比节点关键值数多1)return children[i].get(key);}//写一个方法,向 keys 指定索引 index 处插入 keyvoid insertKey(int key, int index){for (int i = keyNumber-1; i >= index ; i--) {keys[i+1] = keys[i];}keys[index] = key;keyNumber++;}//写一个方法,向 children 指定索引 index 处插入 childvoid insertChild(Node child, int index){System.arraycopy(children,index,children,index+1,keyNumber);children[index] = child;}//移除指定index处的keyint removeKey(int index){int t = keys[index];System.arraycopy(keys,index+1,keys,index,--keyNumber-index);return t;}//移除最左边的keyint removeLeftmostKey(){return removeKey(0);}//移除最右边的keyint removeRightmostKey(){return removeKey(keyNumber-1);}//移除指定index处的childNode removeChild(int index){Node node = children[index];children[index] = null;return children[index];}//移除最左边的childNode removeLeftmostChild(){return removeChild(0);}//移除最右边的childNode removeRightmostChild(){return removeChild(keyNumber);}//返回index孩子处左边的兄弟Node childLeftSibling(int index){return index > 0 ? children[index-1]:null;}//返回index孩子处右边的兄弟Node childRightSibling(int index){return index == keyNumber ? null : children[index+1];}//复制当前节点的所有key和child到targetvoid moveToTarget(Node target){int start = target.keyNumber;if (!leaf){for (int i = 0; i <= keyNumber; i++) {target.children[start+i] = children[i];}}for (int i = 0; i < keyNumber; i++) {target.keys[target.keyNumber++] = keys[i];}}}Node root; //定义一个根节点int t; //树中节点的最小度数(就是一个节点的最小孩子数,根节点叶子节点除外)final int MIN_KEY_NUMBER;//最小关键字的数量final int MAX_KEY_NUMBER;//最大关键字的数量//无参构造,最小度数默认值为2public L5_BTree() {this(2);}//有参构造public L5_BTree(int t) {this.t = t;root = new Node(t);//new出根节点,并给出根节点最小度数MIN_KEY_NUMBER = t-1;MAX_KEY_NUMBER = 2*t-1;}//判断关键字中是否存在指定关键字对应的节点public boolean contains(int key){return root.get(key) != null;}//新增一个关键字/**描述一下流程吧* 你构造一颗B树,给定了最小度数,那么最小关键字数、最大关键字数、阶数也就都定了* 你开始往节点中插入关键值,一开始没满,你继续插入* 当插入的关键字数等于最大关键字数时,这个节点就要分裂了,即将自身的关键字分出去,变为孩子节点* 然后你再插入,它就会按照关键字的顺序去选位置,* 如果找到位置了,是叶子节点,那么就直接插入(当然超过MAX_KEY_NUMBER就分裂一下)* 如果恰好发现一个非叶子节点里面也有位置,那么应该先搜索一下这个节点的孩子,然后再进行判断插在哪里* 当某个节点的关键字数再满,那这个树就再分裂一次* */public void put(int key){doPut(root,key,null,0);}//递归的函数private void doPut(Node node,int key,Node parent,int index){int i = 0;while (i < node.keyNumber){if (node.keys[i] == key){return; //更新逻辑}if (node.keys[i] > key){break; //找到插入位置,记为i}i++;}if (node.leaf){node.insertKey(key,i);//可能到达上限}else {doPut(node.children[i],key,node,i);//可能到达上限}if (node.keyNumber == MAX_KEY_NUMBER){split(node,parent,index);}}//分裂函数/*** left:要分裂的节点* parent:分裂节点的父节点* index:分裂节点是第几个孩子* */private void split(Node left, Node parent, int index){if (parent == null){//分裂的是根节点Node newRoot = new Node(t);newRoot.leaf = false;newRoot.insertChild(left,0);this.root = newRoot;parent = newRoot;}//1.创建right节点,把left中t之后的key和child移动过去Node right = new Node(t);right.leaf = left.leaf;System.arraycopy(left.keys,t,right.keys,0,t-1);//分裂节点是非叶子节点的情况if (!left.leaf){System.arraycopy(left.children,t,right.children,0,t);}right.keyNumber = t-1;left.keyNumber = t-1;//2.中间的key(t-1处)插入到父节点中int mid = left.keys[t-1];parent.insertKey(mid,index);//3.right节点作为父节点的孩子parent.insertChild(right,index+1);}//删除一个关键字public void remove(int key){doRemove(null,root,0,key);}private void doRemove(Node parent,Node node,int index,int key){int i = 0;while (i < node.keyNumber){if (node.keys[i] >= key){break;}i++;}//找到了,代表待删除key的索引//没找到,表示到第 i 个孩子里面继续查找if (node.leaf){if(!found(node, key, i)){//case1return;}else {//case2node.removeKey(i);}}else {if(!found(node, key, i)){//case3doRemove(node,node.children[i],i,key);}else {//case4Node s = node.children[i+1];while (!s.leaf){s = s.children[0];}int skey = s.keys[0];node.keys[i] = skey;doRemove(node,node.children[i+1],i+1,skey);}}if (node.keyNumber < MIN_KEY_NUMBER){//调整平衡 case5 and case6balance(parent,node,index);}}private void balance(Node parent, Node x, int i){//case6 根节点if (x == root){if (root.keyNumber == 0 && root.children[0] != null){root = root.children[0];}return;}Node left = parent.childLeftSibling(i);Node right = parent.childRightSibling(i);if (left != null && left.keyNumber > MAX_KEY_NUMBER){//case5-1 左边富裕 右旋//把父节点中前驱key旋转下来x.insertKey(parent.keys[i-1],0);if (!left.leaf){//left中最大的孩子换爹x.insertChild(left.removeRightmostChild(),0);}//left中最大的key旋转上去parent.keys[i-1] = left.removeRightmostKey();return;}if (right != null && right.keyNumber > MAX_KEY_NUMBER){//case5-2 右边富裕 左旋//把父节点中后继key旋转下来x.insertKey(parent.keys[i],x.keyNumber);//right中最小的孩子换爹if (!right.leaf){x.insertChild(right.removeLeftmostChild(),x.keyNumber+1);}//right中最小的key旋转上去parent.keys[i] = right.removeLeftmostKey();return;}//case5-3 两边都不富裕 向左合并if(left != null){//向左兄弟合并parent.removeChild(i);left.insertKey( parent.removeKey(i-1), left.keyNumber);x.moveToTarget(left);}else {//自己合并parent.removeChild(i+1);x.insertKey(parent.removeKey(i),x.keyNumber );right.moveToTarget(x);}}private boolean found(Node node, int key, int i) {return i < node.keyNumber && node.keys[i] == key;}}
为了对应代码中插入和删除的逻辑思路,下面给出两张图来看一下。
节点中插入key值后的节点分裂展示图:
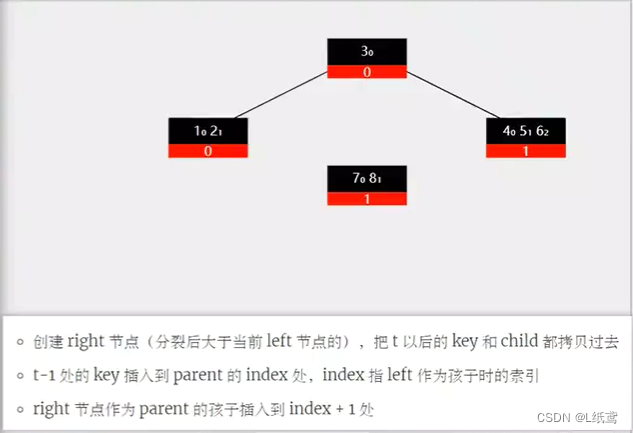
在节点中删除key的6种情况展示图(删除的是某个节点的key):
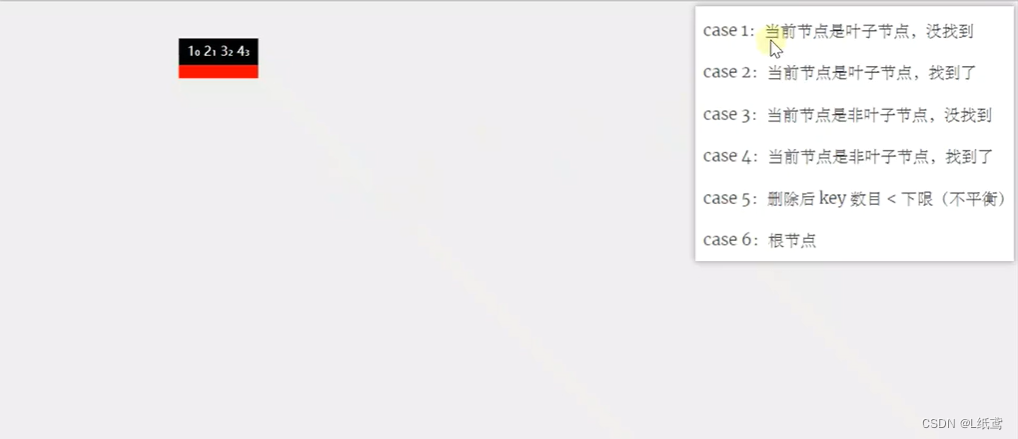
3.小结
说实话,我感觉这东西挺难的,写完之后脑瓜子都嗡嗡的。没有在纸上画图,单靠脑子想,我是肯定写不出来的,所以我的建议是:一定一定一定要画图,一定一定一定要看着图对着代码来一步一步的走,一定一定一定要看图!
相关文章:

数据结构与算法——20.B-树
这篇文章我们来讲解一下数据结构中非常重要的B-树。 目录 1.B树的相关介绍 1.1、B树的介绍 1.2、B树的特点 2.B树的节点类 3.小结 1.B树的相关介绍 1.1、B树的介绍 在介绍B树之前,我们回顾一下我们学的树。 首先是二叉树,这个不用多说ÿ…...
Tomcat源码解析——Tomcat的启动流程
一、启动脚本 当我们在服务启动Tomcat时,都是通过执行startup.sh脚本启动。 在Tomcat的启动脚本startup.sh中,最终会去执行catalina.sh脚本,传递的参数是start。 在catalina.sh脚本中,前面是环境判断和初始化参数,最终…...
蓝桥杯真题演练:2023B组c/c++
日期统计 小蓝现在有一个长度为 100 的数组,数组中的每个元素的值都在 0 到 9 的范围之内。 数组中的元素从左至右如下所示: 5 6 8 6 9 1 6 1 2 4 9 1 9 8 2 3 6 4 7 7 5 9 5 0 3 8 7 5 8 1 5 8 6 1 8 3 0 3 7 9 2 7 0 5 8 8 5 7 0 9 9 1 9 4 4 6 8 6 3 …...
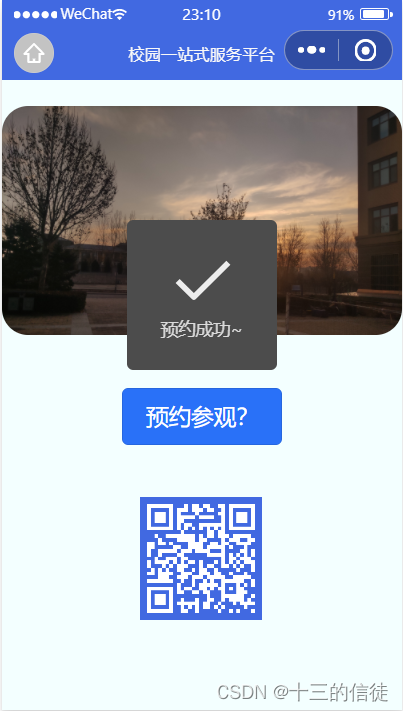
微信小程序实现预约生成二维码
业务需求:点击预约按钮即可生成二维码凭码入校参观~ 一.创建页面 如下是博主自己写的wxml: <swiper indicator-dots indicator-color"white" indicator-active-color"blue" autoplay interval"2000" circular > &…...

专业140+总分410+北京理工大学826信号处理导论考研经验北理工电子信息通信工程,真题,参考书,大纲。
今年考研专业课826信号处理导论(信号系统和数字信号处理)140,总分410,顺利上岸!回看去年将近一年的复习,还是记忆犹新,有不少经历想和大家分享,有得有失,希望可以对大家复…...

做一个后台项目的架构
后台架构的11个维度 架构1:团队协助基础工具链的选型和培训架构2:搭建微服务开发基础设施架构3:选择合适的RPC框架架构4:选择和搭建高可用的注册中心架构5:选择和搭建高可用的配置中心架构6:选择和搭建高性…...
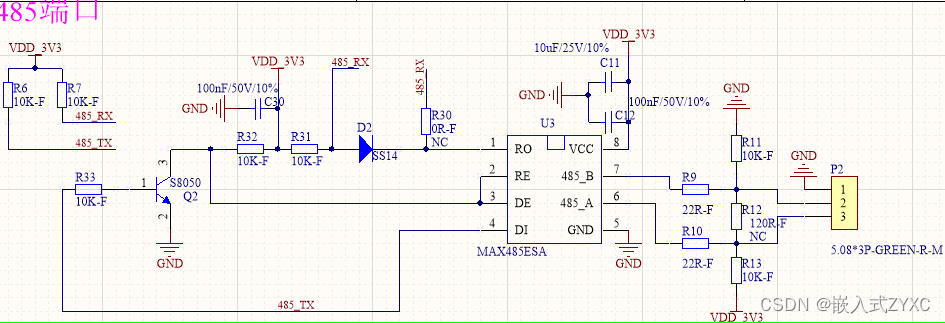
嵌入式单片机 TTL电平、232电平、485电平的区别和联系
一、简介 TTL、232和485是常见的串口通信标准,它们在电平和通信方式上有所不同, ①一般情况下TTL电平应用于单片机外设,属于MCU/CPU等片外外设; ②232/485电平应用于产品整体对外的接口,一般是片外TTL串口转232/485…...
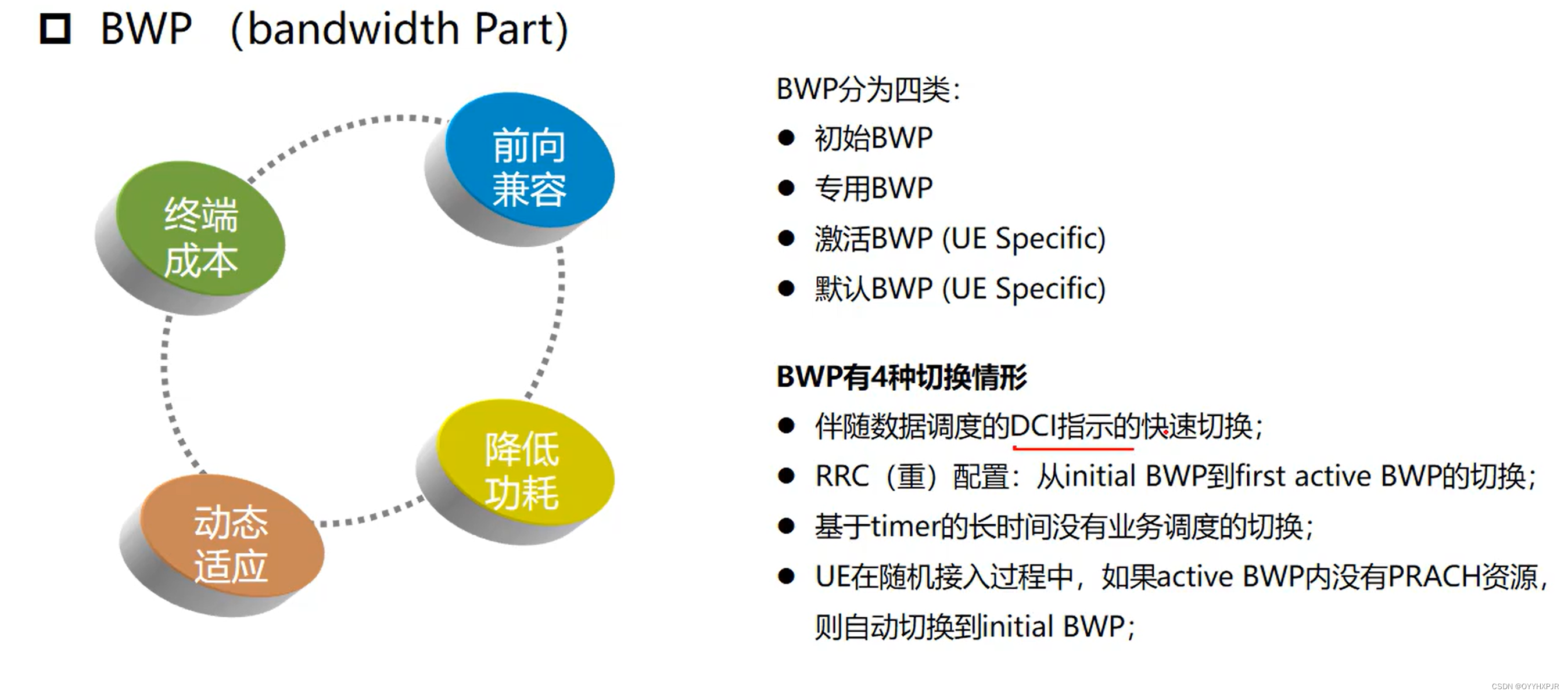
2024年大唐杯备考
努力更新中…… 第一章 网络架构和组网部署 1.1 5G的网络整体架构 5G网络中的中传、回传、前传(这里属于承载网的概念) CU和DU之间是中传 BBU和5GC之间是回传 BBU和AAU之间是前传(这个好记) 这里竟然还藏了MEC(…...
:Spring Boot与MySQL搭配,打造极简高效的数据管理系统)
Spring Boot(06):Spring Boot与MySQL搭配,打造极简高效的数据管理系统
1. 前言 Spring Boot 是一个基于Spring框架的快速开发框架,可以使开发者快速搭建一个可靠的Java Web应用程序。而MySQL是最广泛使用的关系型数据库系统之一,也是Spring Boot整合数据库的首选。本文将介绍Spring Boot如何整合MySQL数据库。 2. 摘要 本文…...

Vue3 + Vite 构建组件库发布到 npm
你有构建完组件库后,因为不知道如何发布到 npm 的烦恼吗?本教程手把手教你用 Vite 构建组件库发布到 npm 搭建项目 这里我们使用 Vite 初始化项目,执行命令: pnpm create vite my-vue-app --template vue这里以我的项目 vue3-xm…...

Vite多环境配置与打包:灵活高效的Vue开发工作流
🌟 前言 欢迎来到我的技术小宇宙!🌌 这里不仅是我记录技术点滴的后花园,也是我分享学习心得和项目经验的乐园。📚 无论你是技术小白还是资深大牛,这里总有一些内容能触动你的好奇心。🔍 &#x…...
从零实现诗词GPT大模型:数据集介绍和预处理
专栏规划: https://qibin.blog.csdn.net/article/details/137728228 本章将介绍该系列文章中使用的数据集,并且编写预处理代码,处理成咱们需要的格式。 一、数据集介绍 咱们使用的数据集名称是chinese-poetry,是一个在github上开源的中文诗…...
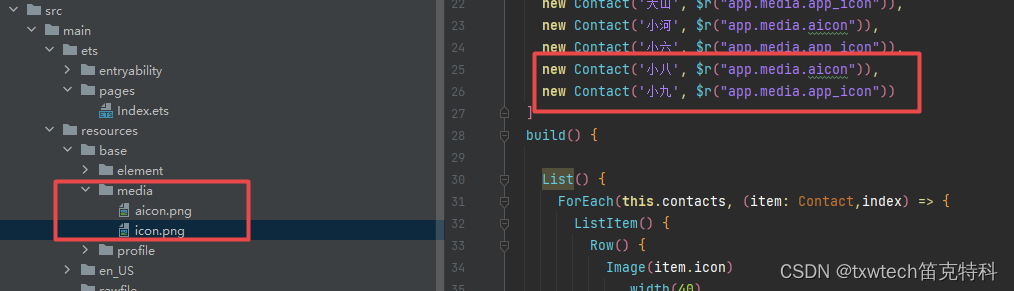
45.HarmonyOS鸿蒙系统 App(ArkUI)创建列表(List)
列表是一种复杂的容器,当列表项达到一定数量,内容超过屏幕大小时,可以自动提供滚动功能。它适合用于呈现同类数据类型或数据类型集,例如图片和文本。在列表中显示数据集合是许多应用程序中的常见要求(如通讯录、音乐列…...

推荐算法之协同过滤
算法原理 透过百科,我们了解到协同过滤推荐(Collaborative Filtering recommendation)是在信息过滤和信息系统中正迅速成为一项很受欢迎的技术。与传统的基于内容过滤直接分析内容进行推荐不同,协同过滤算法结合用户行为分析用户…...

Kotlin 面试题
lifecycleScope.launchWhenResumed launchWhenResumed是一个扩展函数,它是LifecycleCoroutineScope的一部分,并且它是在Android的Lifecycle库中引入的。 这个函数的主要目的是在Lifecycle的对应组件(通常是Activity或Fragment)处于“resumed”状态时启动协程。 public fun …...

TCM(Tightly Coupled Memory)紧密耦合存储器简介
在ARM Cortex处理器中,TCM通常指的是紧密耦合存储器(Tightly Coupled Memory)。TCM是一种位于处理器核心旁边的高速存储器,它的设计目的是为了提供低延迟和高带宽的内存访问性能。 TCM的特点是它与处理器内核紧密耦合,…...

《自动机理论、语言和计算导论》阅读笔记:p172-p224
《自动机理论、语言和计算导论》学习第 8 天,p172-p224总结,总计 53 页。 一、技术总结 1.Context-Free Grammar(CFG) 2.parse tree (1)定义 p183,But perhaps more importantly, the tree, known as a “parse tree”, when used in a …...

typescript playwright 笔记
录制调式 命令 npx playwright codegen url npx playwright codegen https://www.baidu.com/typescript 中 format 和 split 的使用 import * as util from util;const str1 hellow %s; const format util.format; const str2 format(str1, word);// 提取taskId const str3…...

从零实现诗词GPT大模型:了解Transformer架构
专栏规划: https://qibin.blog.csdn.net/article/details/137728228 这篇文档我们开始对GPT的核心组件Transformer进行一个详细的讲解, 加急编写中…...

温故知新之-TCP Keepalive机制及长短连接
[学习记录] 前言 TCP连接一旦建立,只要连接双方不主动 close ,连接就会一直保持。但建立连接的双方并不是一直都存在数据交互,所以在实际使用中会存在两种情况:一种是每次使用完,主动close,即短连接&…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
