0基础刷图论最短路 3(从ATcoder 0分到1800分)
AT最短路刷题3(本文难度rated 1200~ 1400)
题目来源:Atcoder
题目收集:
https://atcoder-tags.herokuapp.com/tags/Graph/Shortest-Path
(里面按tag分类好了Atcoder的所有题目,类似cf)
(访问需要魔法)
这算是一个题单,各位有兴趣可以按照这个顺序来刷。
我的代码仅供参考。
会提示关键性质和步骤。 部分有注释。
洛谷、知乎、可以搜到题解。
文章目录
- AT最短路刷题3(本文难度rated 1200~ 1400)
- 1-**身体バランス**
- 2-**Road Reduction**
- **3 - Swap Places**
- 4-**Come Back Quickly**
- 5-**正直者の高橋くん**
- 6-**joisino's travel**
- 7-**Traveler**
- 8- **Merge Set**
1-身体バランス
这道题其实就是求两边dijkstra
一遍正图
一遍反图然后枚举每个点,
1 --> i 的路径长度 == i--> n 的路径长度
并且, dist1[i]+dist2[i] == dist1[n]然后找有没有这样的点就行了。贴答案ing
#include <bits/stdc++.h>#define rep(i,n) for(int i=0;i<(n);i++)using namespace std;template<class T> struct edge{int to;T wt;edge(int to,const T& wt):to(to),wt(wt){}
};
template<class T> using weighted_graph=vector<vector<edge<T>>>;template<class T>
vector<T> Dijkstra(const weighted_graph<T>& G,int s){const T INF=numeric_limits<T>::max();int n=G.size();vector<T> d(n,INF); d[s]=0;priority_queue<pair<T,int>> Q; Q.emplace(0,s);while(!Q.empty()){T d0=-Q.top().first;int u=Q.top().second; Q.pop();if(d0>d[u]) continue;for(const auto& e:G[u]){int v=e.to;if(d[v]>d[u]+e.wt) d[v]=d[u]+e.wt, Q.emplace(-d[v],v);}}return d;
}const int INF=1<<29;int main(){int n,m,s,t; scanf("%d%d%d%d",&n,&m,&s,&t); s--; t--;weighted_graph<int> G(n);rep(i,m){int u,v,c; scanf("%d%d%d",&u,&v,&c); u--; v--;G[u].emplace_back(v,c);G[v].emplace_back(u,c);}auto d1=Dijkstra(G,s);auto d2=Dijkstra(G,t);rep(u,n) if(d1[u]<INF && d1[u]==d2[u]) return printf("%d\n",u+1),0;puts("-1");return 0;
}2-Road Reduction
最短路
https://atcoder.jp/contests/abc252/tasks/abc252_e
一张图,有N个点。
M条边。
现在我们要删除一些边,最终会剩下N-1条边。然后,求出:
1到每个城市的最短路径这个问题只是看上去很唬人。我们只要知道一个事情:
如果一张图是连通的,那么它的边最少都要是N-1由于,最短路只会比这个多,不会比这个少。
所以,直接跑最短路。
拓展到谁就是谁。#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define PII pair<int,pair<int,int>>
#define INF 1e18
const int N = 2e5+7;
struct node{int v;int w;int id; //edge编号
};
struct edge{int u;int id;int step;bool operator<(edge b)const{return step>b.step;}
};
vector<node> g[N];
int dist[N];
int flag[N];
int n,m;void dijkstra(){for(int i=1;i<=n;i++)dist[i]=INF;dist[1]=0;priority_queue<edge> q;q.push(edge{1,-1,0});while(q.size()){int u = q.top().u;int id = q.top().id;q.pop();if(flag[u])continue;flag[u]=1;if(id!=-1){cout<< id<<' ';}for(auto i:g[u]){int v = i.v;int w = i.w;int id = i.id;if(dist[v]>dist[u]+w){dist[v]=dist[u]+w;q.push(edge{v,id,dist[v]});}}}
}
void slove(){cin>>n>>m;for(int i=1;i<=m;i++){int u,v,w;cin>>u>>v>>w;g[u].push_back(node{v,w,i});g[v].push_back(node{u,w,i});}dijkstra();
}signed main(){slove();
}
3 - Swap Places
https://atcoder.jp/contests/abc289/tasks/abc289_e]
BFS 存两个点状态
/*
一种新类型
想过双搜,但其实这比双搜简单。
因为他有限制条件。1、它们两个移动到的顶点必须是不同颜色
2、它们两个要同时到达起点和终点然后我们再思考一下flag这么写?
是一个点不能重复,还是一个状态不能重复。
显然是一个状态,也就是两个人所在的位置不能重复入队我们bfs可不可以回头或者一个人停下来等?为什么要回头?假如一方更快到达,一方更慢到达。需要有人停下来等下。显然这种情况是不会发生的...因为它们两个是同时移动,而不是先后移动。所以只要存在路径它们能一直往前走,那么就可以同时到达。所以我们的flag函数,记录的是:一个状态不可到达两次*/#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define PII pair<int,int>
#define endl "\n"
#define INF 1e18
#define int long long
const int N = 2001; // 1e6 + 5struct node{int n1;int n2;int step;
};
int color[N];
bool flag[N][N];void solve() {memset(color,0,sizeof color);memset(flag,0,sizeof flag);vector<int> g[N];int n,m;cin>>n>>m;for(int i=1;i<=n;i++)cin>>color[i];for(int i=1;i<=m;i++){int u,v;cin>>u>>v;g[u].push_back(v);g[v].push_back(u);}queue<node> q;q.push(node{1,n,0});while(q.size()){int n1 = q.front().n1;int n2 = q.front().n2;int step = q.front().step;q.pop();if(flag[n1][n2])continue;flag[n1][n2]=1;if(n1==n and n2==1){cout<<step<<endl;return;}for(auto i:g[n1]){for(auto j:g[n2]){if(color[i]!=color[j])q.push({i,j,step+1});}}}cout<<-1<<endl;}
signed main () {std::ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);int t;cin>> t;while(t --)solve();
}
4-Come Back Quickly
https://atcoder.jp/contests/abc191/tasks/abc191_e
dijkstra
/*
对于每个城镇,我们需要找到一个城镇:1、从起点出发走到那里还能再回来
2、出发+回来的时间最短N=2000
跑2000遍最短路。对于每个起点 ,更新 dist[i][j]
跑完之后,
对于每个起点,找到一个点使得 dist[i][j]+dist[j][i] 最短
如果i==j 那么只加一遍。关于输入:
对于同一对点,只取最短的路。
一开始全部初始为INF*/#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define PII pair<int,int>
#define INF 1e18
const int N =2001;
int n,m;
struct node{int v;int w;
};
vector<node> g[N];
int dist[N];
bool flag[N];
int d[N][N];void dijkstra(int start){for(int i=1;i<=n;i++) dist[i]=INF;for(int i=1;i<=n;i++) flag[i]=0;dist[start]=0;priority_queue<PII,vector<PII>,greater<PII>> q;q.push({0,start});while(q.size()){int u = q.top().second;q.pop();if(flag[u])continue;flag[u]=1;for(auto i:g[u]){int v =i.v;int w =i.w;if(dist[v]>dist[u]+w){dist[v]=dist[u]+w;d[start][v] = min(d[start][v],dist[v]);q.push({dist[v],v});}}}}
void slove(){cin>>n>>m;for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)d[i][j]=INF;for(int i=1;i<=m;i++){int u,v,w;cin>>u>>v>>w;d[u][v]=min(d[u][v],w);}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i!=j){if(d[i][j]!=INF)g[i].push_back(node{j,d[i][j]});}}}for(int i=1;i<=n;i++){dijkstra(i);}for(int i=1;i<=n;i++){int ans = INF;for(int j=1;j<=n;j++){if(i==j){ans = min(ans,d[i][j]);}else{ans = min(ans,d[i][j]+d[j][i]);}}if(ans==INF)cout<<-1<<endl;else cout<<ans<<endl;}}signed main(){slove();
}
5-正直者の高橋くん
https://atcoder.jp/contests/abc021/tasks/abc021_c
dp+dijkstra
/*
新的题型:求起点到终点,的最短路有多少条。考虑dp设dp[i][j]表示从起点出发,走到i,且距离为j的路的数量假设结尾是end,
答案是 dp[end][dist];那么从所有能扩展到end的点中
dp[end][dist] += dp[i][dist-1]我们考虑初始是怎么得到状态的:从起点开始扩展:dp[v][j] += dp[u][j-1]初始化就是
dp[start][0]=1;
*/
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define PII pair<int,int>
#define INF 1e18
const int mod = 1e9+7;
const int N = 101;
int dp[101][1000]; //答案
int dist[101]; //最短路
bool flag[101];
vector<int> g[N];int a,b; //起点终点
int n,m;void dijkstra(){for(int i=1;i<=n;i++)dist[i]=INF;dist[a]=0;dp[a][0]=1;priority_queue<PII,vector<PII>,greater<PII>> q;q.push({0,a});while(q.size()){int u = q.top().second;q.pop();if(flag[u])continue;flag[u]=1;for(auto i:g[u]){if(dist[i]>=dist[u]+1){dist[i]=dist[u]+1;dp[i][dist[i]]=( dp[i][dist[i]]+dp[u][dist[u]])%mod;q.push({dist[i],i});}}}cout<<dp[b][dist[b]]%mod<<endl;
}
void slove(){cin>>n;cin>>a>>b;cin>>m;for(int i=1;i<=m;i++){int u,v;cin>>u>>v;g[u].push_back(v);g[v].push_back(u);}dijkstra();}signed main(){slove();
}
6-joisino’s travel
https://atcoder.jp/contests/abc073/tasks/abc073_d
floyd + 全排列
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;int n,m,R,dist[300][300],r[10];int main()
{memset(dist,0x3f,sizeof dist);int Min,ans;cin>>n>>m>>R;for(int i=0;i<R;i++)cin>>r[i];for(int i=0;i<m;i++){int x,y,z;cin>>x>>y>>z;dist[x][y]=dist[y][x]=z;}for(int k=1;k<=n;k++)for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)if(dist[i][k]+dist[k][j]<dist[i][j])dist[i][j]=dist[i][k]+dist[k][j];sort(r,r+R);ans=0x3f3f3f3f;do{Min=0;for(int i=0;i<R-1;i++)Min+=dist[r[i]][r[i+1]];ans=min(Min,ans);}while(next_permutation(r,r+R));cout<<ans;
}
7-Traveler
https://atcoder.jp/contests/abc197/tasks/abc197_e
/*
这是一个新问题:
如果你必须要走完所有点 or 必须走完所选中的点。
你的最短路是多少?建图:如果小球ID一样,那么两者之间建立双向边。标记数组:
标记每个球其实最终这是一条链。
因为对于id不一样的小球,我们是线性升序的,也就是一条链but... 对于ID一样的小球,我们必须采用特定的顺序。使之变成一条链。对于id一样的小球,我们只关心分布两端的球。
中间的球在拣两端的球的路上会被捡走。而对于同一种id的小球,我们最后拣左端 还是 拣右段 是不知道的 。这需要跟下一种要捡的id有关。
而。。下一种要捡的id,也是找左端和右段。显然,状态有点太多了。
所以考虑dp设dp[i][2]表示当前是 id = i的小球,我们最后一次是捡 0左边/1右边 的最短路假设序列已经排好序:捡左边: abs(now - d[1]) + abs(d[k] - d[1])
显然,我们还需要一个中间变量记录每一种id开始捡的时候的坐标。捡右边:abs(now - d[k]) + abs(d[1]-d[k]) ;*/#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define PII pair<int,int>
#define INF 1e18
const int N = 2e5+7;
int dp[N][2];
set<int> color;
vector<int> g[N];
void slove(){int n;cin>>n;for(int i=1;i<=n;i++){int x,c;cin>>x>>c;color.insert(c);g[c].push_back(x);}for(auto i:color){sort(g[i].begin(),g[i].end());}int now = 0;for(auto i = color.begin() ; i!=color.end();i++){int id = *i;auto it = i;auto is = it;if(it!=color.begin()){is--;int pre = *is; //上一次的小球id//当前id的小球,最后一次收集是左边:// 上一次的小球收集最后是在左边:int temp1 = dp[pre][0] + abs(g[pre][0]-g[id][g[id].size()-1]) + abs(g[id][0]-g[id][g[id].size()-1]);//上一次的小球收集在右边int temp2 = dp[pre][1] + abs(g[pre][g[pre].size()-1]-g[id][g[id].size()-1]) + abs(g[id][0]-g[id][g[id].size()-1]);dp[id][0] = min(temp1,temp2);//当前id的小球,最后一次收集在右边:// 上一次的小球收集最后是在左边:temp1 = dp[pre][0] + abs(g[pre][0]-g[id][0]) + abs(g[id][0]-g[id][g[id].size()-1]);//上一次的小球收集在右边temp2 = dp[pre][1] + abs(g[pre][g[pre].size()-1]-g[id][0]) + abs(g[id][0]-g[id][g[id].size()-1]);dp[id][1] = min(temp1,temp2);}else{//当前id的小球,最后一次收集是左边:// 上一次的在起点:int temp1 = 0 + abs(0-g[id][g[id].size()-1]) + abs(g[id][0]-g[id][g[id].size()-1]);//上一次的在起点:int temp2 = 0 + abs(0-g[id][g[id].size()-1]) + abs(g[id][0]-g[id][g[id].size()-1]);dp[id][0] = min(temp1,temp2);//当前id的小球,最后一次收集在右边:// 上一次的在起点:temp1 = 0 + abs(0-g[id][0]) + abs(g[id][0]-g[id][g[id].size()-1]);//上一次的在起点:temp2 = 0 + abs(0-g[id][0]) + abs(g[id][0]-g[id][g[id].size()-1]);dp[id][1] = min(temp1,temp2);}}// 加上回到起点的距离cout<<min(dp[*color.rbegin()][1]+abs(g[*color.rbegin()][g[*color.rbegin()].size()-1]),dp[*color.rbegin()][0] + abs(g[*color.rbegin()][0]) )<<endl;}signed main(){slove();
}
8- Merge Set
https://atcoder.jp/contests/abc302/tasks/abc302_f
警钟长鸣:N要开大点
/*
一共有N个集合
每个集合包含图内的一些点。当前仅当,两个集合内有交点,那么我们可以将这两个集合合并集合内部是互通的。我们现在要从1,到M请问需要连接多少集合。我们可以在每个集合内部连接一条边权为0的点。在每个集合间连接一条边权为1的点。然后跑一遍最短路。问题是:
如何在集合之间连边?考虑集合之间是如何互通的?这题算是一个套路的建图题。对于这种集合间连边的问题:
我们可以给每个集合都编号。这个编号不能和现在有的点重复。
所以可以考虑i+M然后把每个集合内部的点,都和这个集合相连。点到集合的边为0
集合到点的边为1答案就是最短路-1
*/#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define PII pair<int,int>
#define INF 1e18struct node{int v;int w;
};
struct point{int u;int step;bool operator <(point b)const{return step>b.step;}
};const int N = 5e6+6;
int dist[N];
int flag[N];
vector<node> g[N];
void slove(){int n,m;cin>>n>>m;for(int i=1;i<=n;i++){int len;cin>>len;while(len--){int v;int u = i+m;cin>>v;g[v].push_back(node{u,1});g[u].push_back(node{v,1});}}priority_queue<point> q;q.push(point{1,0});while(q.size()){int u = q.top().u;int step = q.top().step;q.pop();if(flag[u])continue;flag[u]=1;if(u==m){cout<<step/2-1<<endl;return;}for(auto i : g[u]){int v = i.v;int w = i.w;q.push(point{v,w+step});}}cout<<-1<<endl;}signed main(){slove();
}
相关文章:
)
0基础刷图论最短路 3(从ATcoder 0分到1800分)
AT最短路刷题3(本文难度rated 1200~ 1400) 题目来源:Atcoder 题目收集: https://atcoder-tags.herokuapp.com/tags/Graph/Shortest-Path (里面按tag分类好了Atcoder的所有题目,类似cf) &#x…...

k8s+docker一键安装过程
环境: k8s 1.20 docker 20.10 centos7.9 #docker安装 yum install -y epel-release yum install -y yum-utils yum-config-manager --add-repo https://mirrors.ustc.edu.cn/docker-ce/linux/centos/docker-ce.repo yum install -y docker-ce-20.10.6 docker-ce-cli-2…...

Python3+Appium+Android SDK+真机+实现app自动化测试-基于Red Hat7.9版本搭建环境及运行python脚本。
1、总体概述? 收费有收费的服务,那就是细致。Red Hat9.0自动化环境也有,需要的说一声。 1、实现在Red Ha/t Enterprise Linux7.9环境中搭建部署app自动化测试环境,提供详细步骤。 2、版本说明:jdk8/17+nodejs16/18/19/20/21+android sdk29+python3.9.18/3.11.1+appium1…...

深入理解MD5算法:原理、应用与安全
title: 深入理解MD5算法:原理、应用与安全 date: 2024/4/11 20:55:57 updated: 2024/4/11 20:55:57 tags: MD5算法数据安全哈希函数摘要算法安全漏洞SHA算法密码学 第一章:引言 导言 在当今数字化时代,数据安全和完整性变得至关重要。消息…...
- Java API)
架构师系列-搜索引擎ElasticSearch(三)- Java API
SpringBoot整合ES 搭建SpringBoot工程,引入ElasticSearch相关坐标 <!--引入es的坐标--><dependency><groupId>org.elasticsearch.client</groupId><artifactId>elasticsearch-rest-high-level-client</artifactId><versi…...

Ubuntu下配置Android NDK环境
Android-NDK的下载 下载Android-NDK wget -c http://dl.google.com/android/ndk/android-ndk-r10e-linux-x86_64.bin 执行bin文件(即解压) ./android-ndk-r10c-linux-x86_64.bin Android-NDK的配置 要想使用Android-NDK,还需要进行环境变量…...
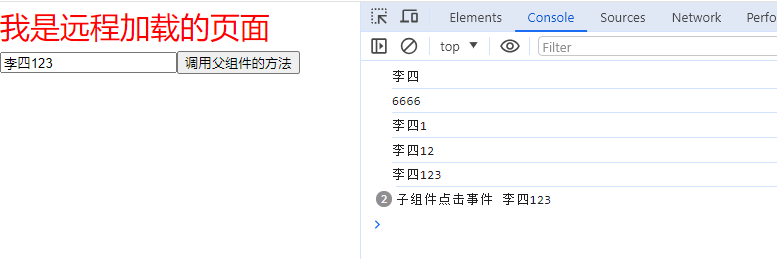
使用 vue3-sfc-loader 加载远程Vue文件, 在运行时动态加载 .vue 文件。无需 Node.js 环境,无需 (webpack) 构建步骤
加载远程Vue文件 vue3-sfc-loader vue3-sfc-loader ,它是Vue3/Vue2 单文件组件加载器。 在运行时从 html/js 动态加载 .vue 文件。无需 Node.js 环境,无需 (webpack) 构建步骤。 主要特征 支持 Vue 3 和 Vue 2(参见dist/)仅需…...
stm32移植嵌入式数据库FlashDB
本次实验的程序链接stm32f103FlashDB嵌入式数据库程序资源-CSDN文库 一、介绍 FlashDB 是一款超轻量级的嵌入式数据库,专注于提供嵌入式产品的数据存储方案。与传统的基于文件系统的数据库不同,FlashDB 结合了 Flash 的特性,具有较强的性能…...

Ubuntu 安装Java、Git、maven、Jenkins等持续集成环境
Ubuntu 持续集成 安装OpenJdk 查看所有可安装的 JDK 版本 apt list OpenJDK\*使用 apt 安装 JDK(以 11为例),最好是用11,java8对应的jenkins会有兼容问题。 sudo apt install openjdk-11-jdk openjdk-11-jre安装成功后,可以使用以…...
文件批量重命名并批量修改文件扩展名,支持随机大小写字母命名并修改扩展名字母
在数字时代,文件的管理和整理成为了我们日常工作与生活中不可或缺的一部分。然而,面对堆积如山的文件,如何高效地对其进行重命名和修改扩展名,成为了许多人的难题。 第一步,进入文件批量改名高手的主页面,…...
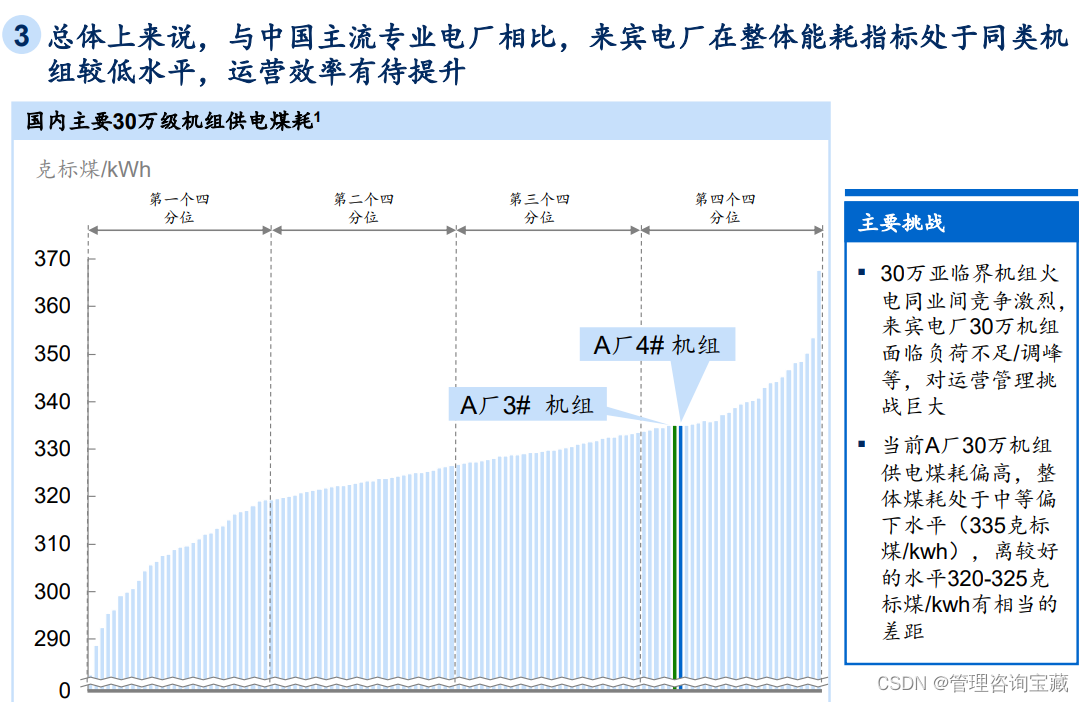
【管理咨询宝藏70】MBB大型城投集团内外部环境分析报告
本报告首发于公号“管理咨询宝藏”,如需阅读完整版报告内容,请查阅公号“管理咨询宝藏”。 【管理咨询宝藏70】MBB大型城投集团内外部环境分析报告 【格式】PDF版本 【关键词】战略规划、商业分析、管理咨询、MBB顶级咨询公司 【强烈推荐】 这是一套市…...

服务器挖矿病毒解决ponscan,定时任务解决
服务器挖矿病毒解决ponscan,定时任务解决 挖矿病毒会隐藏chattr的操作权限,让我们无法删除病毒文件,杀掉病毒进程。所以要去下载chattr.c的文件,编译成a.out。然后再对原来的chattr文件的权限进行修改。然后覆盖掉它。 chattr.c …...
【鸿蒙开发】第二十一章 Media媒体服务(二)--- 音频播放和录制
1 AVPlayer音频播放 使用AVPlayer可以实现端到端播放原始媒体资源,本开发指导将以完整地播放一首音乐作为示例,向开发者讲解AVPlayer音频播放相关功能。 以下指导仅介绍如何实现媒体资源播放,如果要实现后台播放或熄屏播放,需要…...
:Windows安全事件应急响应之Windows应急响应基础必备技能)
网络安全从入门到精通(特别篇I):Windows安全事件应急响应之Windows应急响应基础必备技能
Windows应急 询问攻击情况范围 事件发生时的状况或安全设备告警等,能帮助应急处置人员快速分析确定事件类型,方便前期准备。 通用排查思路 入侵肯定会留下痕迹,另外重点强调的是不要一上来就各种查查查,问清楚谁在什么时间发现的主机异常情况,异常的现象是什么,受害用…...
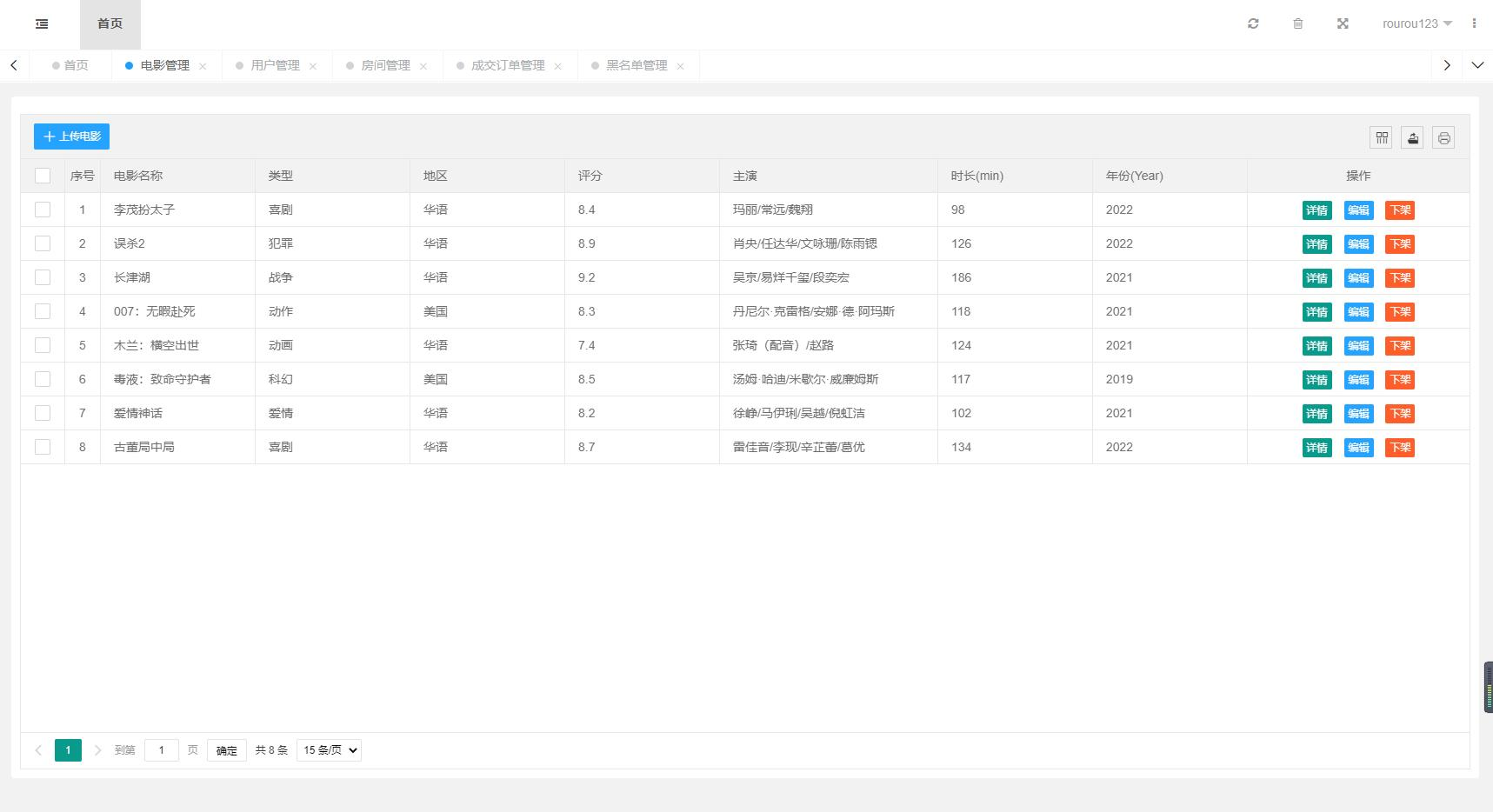
基于SpringBoot+Mybatis框架的私人影院预约系统(附源码,包含数据库文件)
基于SpringBootMybatis框架的私人影院预约系统,附源码,包含数据库文件。 非常完整的一个项目,希望能对大家有帮助哈。 本系统的完整源码以及数据库文件都在文章结尾处,大家自行获取即可。 项目简介 该项目设计了基于SpringBoo…...
【SERVERLESS】AWS Lambda上实操
通过Serverless的发展历程及带给我们的挑战,引出我们改如何改变思路,化繁为简,趋利避害,更好的利用其优势,来释放企业效能,为创造带来无限可能。 一 Serverless概述 无服务器计算近年来与云原生计算都是在…...

IDEA2023 开发环境配置
目录 1. 关闭IDEA自动更新1.2 IDEA 新版样式切换 2. Maven配置2.1本地仓库优先加载2.2 maven.config配置文件中 3. 全局配置JDK4. 配置文件编码:UTF-85. 开启自动编译(全局配置)6. 开启自动导包7. 开启鼠标悬浮(提示文档信息)8. 设…...
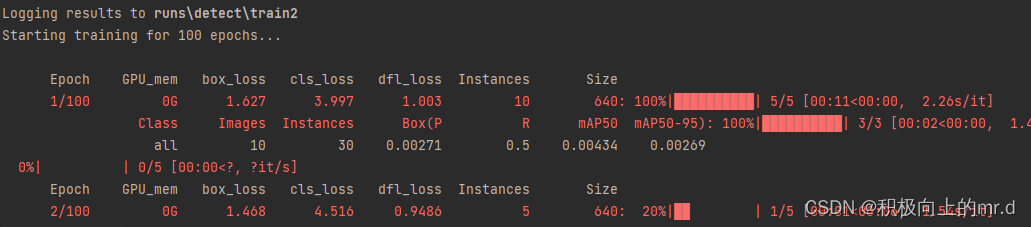
YOLOV5 + 双目相机实现三维测距(新版本)
文章目录 YOLOV5 双目相机实现三维测距(新版本)1. 项目流程2. 测距原理3. 操作步骤和代码解析4. 实时检测5. 训练6. 源码下载 YOLOV5 双目相机实现三维测距(新版本) 本文主要是对此篇文章做一些改进,以及解释读者在…...
计算机网络概述)
【计算机网络】(一)计算机网络概述
文章目录 【计算机网络】(一)计算机网络概述前言1.1 计算机网络在信息时代中的作用1.2 互联网概述1.2.1 网络的网络1.2.2 互联网基础结构发展的三个阶段1.2.3 互联网标准化工作 1.3 互联网的组成1.3.1 互联网的边缘部分1.3.2 互联网的核心部分 1.4 计算机…...

前端npm常用命令总结
npm(Node Package Manager)是Node.js的包管理器,用于安装和管理Node.js的依赖库。以下是一份npm命令的总结文档,涵盖了常用的npm命令及其功能: 包相关的 安装和卸载包 npm install :安装指定名称的包。n…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...
