算法:双指针
算法:双指针
- 双指针
- 快慢指针
- 对撞指针
- 总结
双指针
LeetCode 283.移动零
以上题目要求我们把所有0移动到数组的末尾,也就是说,我们要把数组转化为以下状态:
[ 非0区域 ] [ 0区域 ]
像这种把一个数组划分为多个区域的题型,就是数组划分。而数组划分非常适合使用双指针算法。
对于这道题,我们可以用两个指针,对数组进行动态的区域划分。

其中dest指针维护一段区域,表示非0区域,cur指针与dest之间的区域是0区域。而cur后面的区域是待处理区域。
也就是我们的数组被划分为了以下情况:
[ 非0区域 ][ 0区域 ][ 待处理区域 ]
当我们的cur移动后,对于一个新的数据,就要根据条件来决定把它放到哪一个区域去。当cur指针走到末尾,数组就被处理为了:
[ 非0区域 ][ 0区域 ]
也就是题目要求的样子了。
对于本题而言,如果新插入的数据是0,那就放到cur维护的区域里面,此时直接cur++即可;如果新插入的数据是非0,那么就放到dest的末尾,为了保证dest不会覆盖掉cur原本维护的0,因此要进行一个交换操作。

代码如下:
class Solution
{
public:void moveZeroes(vector<int>& nums) {int dest = -1;int cur = 0;int sz = nums.size();while (cur < sz){if (nums[cur])swap(nums[++dest], nums[cur]);cur++;}}
};
LeetCode 75.颜色分类
这一题也是一个区域划分问题,根据上一题的思路,我们可以把数组划分为以下状态:
[ 0区域 ][ 1区域 ][ 2区域 ]
相比于上一题,这次我们要划分出三个区域来,毫无疑问就需要更多的指针来维护区域,大致可以划分为:
[ 0区域 ][ 1区域 ][ 待处理 ][ 2区域 ]
我们让维护0区域的指针left向右拓展,维护2区域的指针right向左拓展,以及利用cur指针向右遍历数组:

上图中,left指针左侧维护了一段0区域,left与cur之间维护了一段1区域,cur与right之间是待处理区域,right右侧是2区域。当cur往后遍历,如果遇到一个新的数据,就要决定把它放到哪一个区域去:
- 遇到
0,就交换++left与cur的值,把0放到left后面一位,拓展left指针维护的区域- 遇到
1,就直接++cur,把1放到cur与left之间- 遇到
2,就交换--right与cur的值,把2放到right的前面一位,拓展right维护的区域
要注意的是,当把0交给left后,cur++;但是当把2交给right后,cur不能移动。因为left后面的一位数一定是符合cur范围要求的,也就是区间(left, cur]之间的数据被交换到了cur的位置,此时不用判断被交换过来的数据。而right的前面一位数据是不确定的,也就是把区间(cur, right)之间的数据,交换给了cur。而(cur, right)之间的数据是待处理的不确定数据,因此还需要额外判断一次。比如上图中,right的前一位数据就是0,交换后状态如下:

可以看到,cur得到的数据是0,应该被放到left维护的区域去。
总代码如下:
class Solution
{
public:void sortColors(vector<int>& nums){int left = -1;int right = nums.size();int cur = 0;while (cur < right){if (nums[cur] == 0)swap(nums[++left], nums[cur++]);else if (nums[cur] == 2)swap(nums[--right], nums[cur]);//交换后不能cur++,进入下一轮循环在判断一次cur的值elsecur++;}}
};
快慢指针
LeetCode 202.快乐数
该题的意思是,每个数字的下一个数字是该数字所有位的平方和,比如 19 的下一位数字就是 1 2 + 9 2 = 82 1^{2} + 9^{2} = 82 12+92=82。一直以这个规则操作下去,会出现两种情况:
- 最后该数字变为1,那么该数字是快乐数
- 该数字陷入死循环,那么该数字不是快乐数
- 比如
19 -> 82 -> 68 -> 100 -> 1,最后19变成了1,所以19是一个快乐数 - 比如
2 -> 4 -> 16 -> 37 -> 58 -> 89 -> 145 -> 42 -> 20 -> 4,可以发现其陷入了一个死循环,从4开始又以4结束,那么2就不是一个快乐数
这题的难点不在于如何计算下一位快乐数字,而在于如何判断一个数字陷入了死循环。
对于这种循环问题,就可以使用快慢指针。
快慢指针规则如下:
- 定义两个变量
fast与slowfast走2步,slow走一步- 如果
fast走到终点,说明没有循环- 如果
fast与slow相遇,说明陷入了循环
一开始fast和slow都在起点:
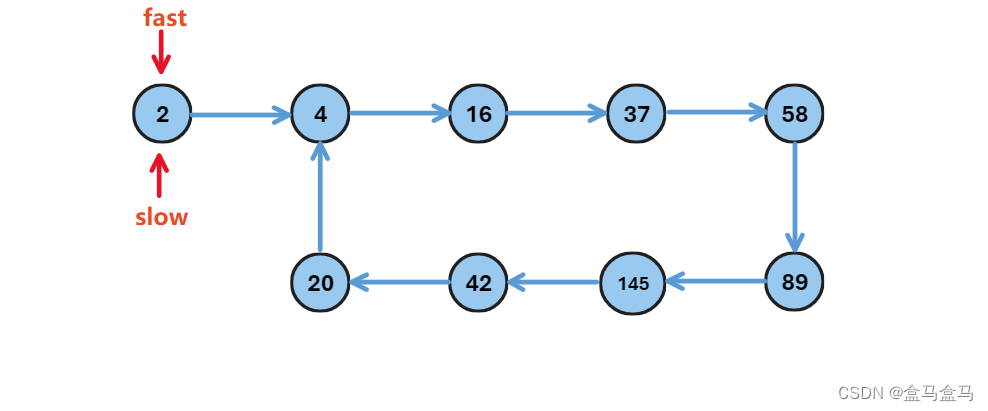
fast走两步,slow走一步:
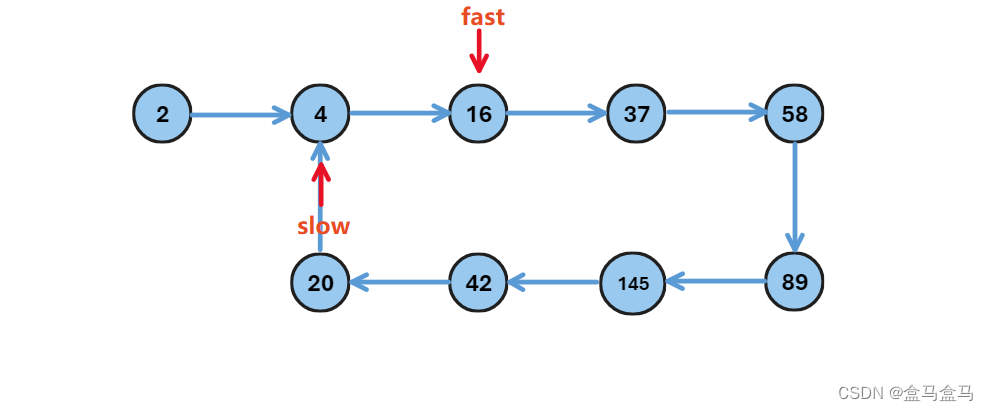
由于这是一个循环结构,当fast进入第二圈循环,slow还没有走完第一圈:
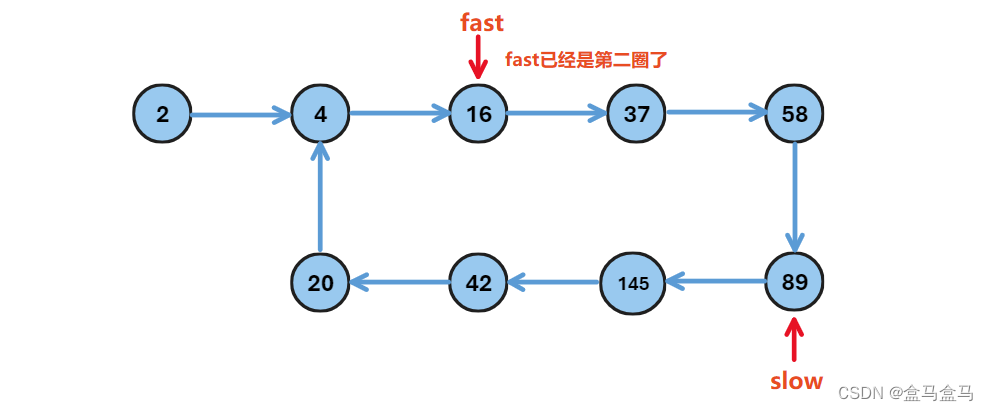
这个时候,由于slow的速度为1,fast的速度为2,那么每次行动fast与slow的距离就会缩短1,最后fast一定可以遇到slow:
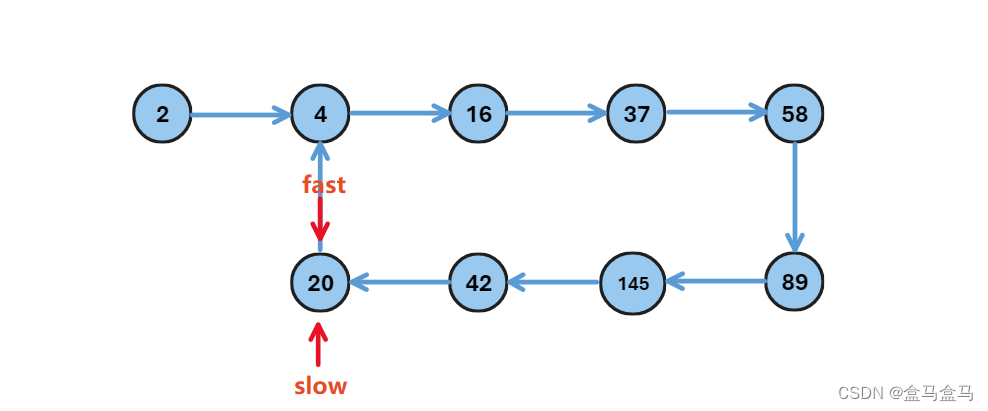
此时两者相遇,说明这是一个循环结构。
因此代码逻辑如下:
- 定义两个变量,
fast和slow,fast走两步,slow走一步- 如果
fast变成1,那么该数字是快乐数,返回true- 如果
fast与slow相遇,那么有循环结构,该数字不是快乐数,返回false
代码如下:
class Solution
{
public:int getNextNum(int n) //到下一个数字的函数{int num = 0;while (n){int tmp = n % 10;num += tmp * tmp;n /= 10;}return num;}bool isHappy(int n) {int fast = n;int slow = n;while (fast != 1){fast = getNextNum(getNextNum(fast));//fast走两步slow = getNextNum(slow);//slow走一步if (fast == slow && fast != 1)//两者相遇,有循环return false;} return true;//到这里说明fast = 1,是快乐数}
};
其中有一个注意点,就是条件fast == slow && fast != 1,这里一种情况就是fast虽然和slow相等,但是两者都为1,此时是快乐数。
比如数字10,10 -> 1 -> 1,slow走第一步就是1了,fast走两步也是1,此时两者相等。
LeetCode 141.环形链表
本题要求判断一个链表中有没有环结构,那就是一个循环问题,要使用快慢指针。
我们刚刚已经讲解过快慢指针了,现在我们直接说明代码逻辑:
- 定义两个指针
fast和slow,fast走两步,slow走一步- 如果
fast为nullptr,说明链表无环,返回true- 如果
fast与slow相遇,说明有环,返回false
代码如下:
class Solution {
public:bool hasCycle(ListNode* head){ListNode* slow = head;ListNode* fast = head;while (fast && fast->next){fast = fast->next->next;slow = slow->next;if (fast == slow)return true;}return false;}
};
注意事项:
- 进入循环时,因为
fast要走两步,因此要判断fast->next是不是空指针,否则fast->next-->next就是访问空指针行为
LeetCode 142.环形链表II
这道题要求我们求出环形链表的环入口,这就麻烦了,通过之前的fast与slow的快慢指针追击问题,我们已经可以判断是否存在环结构了,那么我们要如何求环入口呢?
看到以下示意图:
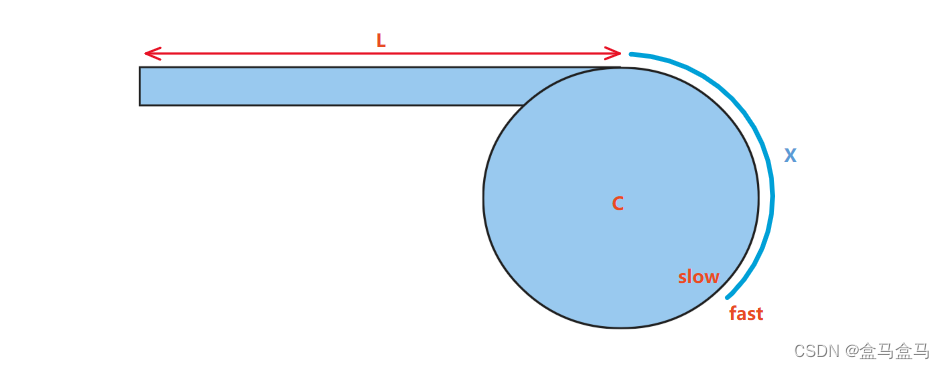
现在slow和fast刚好相遇,参数含义如下:
L:从起点到环入口的距离
C:环周长
X:相遇点和环入口的距离
由于fast的速度是slow的两倍,当slow走的距离是L + X,因此此时fast走了2(L + X)的距离。
又由于fast一定经过了起点到入口的L距离,因此此时fast在环中走了2(L + X) - L = L + 2X的距离。
假设fast已经在环中转了n圈,因此此时fast在环中走了nC + X的距离
那么可以列出公式:
n C + X = L + 2 X nC + X = L + 2X nC+X=L+2X
变形得到:
n C − X = L \mathbf{{\color{Red} nC - X = L} } nC−X=L
这个公式具有重大意义,L代表起点到入口的距离,nC代表n个环周长,X代表当前相遇点与入口的距离。
nC -X整体可以看成(n - 1)C + (C - X),而C - X就代表相遇点开始与环入口的优弧的长度。
此时如果让一个指针A从起点开始走L的距离所用的时间,和让一个指针B从相遇点开始走n - 1圈外加一个C - X的距离所用的时间是一致的。由于相遇点与环入口距离已经是X了,那么指针B最后刚好会走到环入口。而指针A从入口开始走L到达的地方也是环入口,因此两者相遇!
通过这个公式可知:让一个指针从起点开始走,一个指针从相遇点开始走,两者会在环入口相遇!
因此我们的代码逻辑如下:
- 定义两个指针
fast和slow,fast走两步,slow走一步- 如果
fast为nullptr,说明链表无环,返回nullptr- 如果
fast与slow相遇,说明有环,开始找环入口
- 在相遇点定义一个指针
B,也就是B = slow;在起点定义一个指针A,也就是A = head- 两个指针各自行动,速度一致,最后
A与B相遇的地方就是环入口- 返回
A或B
代码如下:
class Solution
{
public:ListNode* detectCycle(ListNode* head){ListNode* fast = head;ListNode* slow = head;while (fast && fast->next){fast = fast->next->next;slow = slow->next;if (slow == fast) // 有环,开始找入口{ListNode* A = head;ListNode* B = slow;while (A != B)//A与B相遇点,就是环入口{A = A->next;B = B->next;}return A;}}return nullptr; //没有环,返回空指针}
};
对撞指针
LCR 179.查找总价格为目标值的两个商品

这道题给了一个升序数组,要求我们求出数组中任意两个值的和刚好为target。
该数组有一个特点:有序数组。像这种在一个有序区间中查找两个元素,计算得到固定值的题型,就可以使用对撞指针。
如果我们直接暴力解法的话,那就是枚举所有两两一对的元素组,直到某一对刚好和为target,时间复杂度为 O ( N 2 ) O(N^{2}) O(N2)。
假设现在的数组为[8, 21, 27, 34, 52],target = 61:
因为数组具有单调性,我们可以一开始就枚举最左侧和左右侧的两个元素:

当前8 + 52 = 60比61小,说明我们需要一个更大的值来增大当前总和。那么由于数组升序,我们只需要left++即可:

当前21 + 52 = 73比61大,说明我们需要一个更小的值来缩小当前总和。那么由于数组升序,我们只需要right--即可:

当前21 + 34 = 55比61小,说明我们需要一个更大的值来增大当前总和。那么由于数组升序,我们只需要left++即可:

当前27 + 34 = 61,我们就找到了目标值,返回left与right下标即可。
正是由于数组单调性,我们可以通过比大小来进行指针的调整,来决定当前总值要变大还是变小,如果最后left与right相遇了,说明不存在这样的和。
为什么可以这样优化呢?看到这个例子:

对于34而言,其要去枚举除了自己以外的所有值,但是当前21 + 34 = 55比61小,如果把21改为8,那只总和只会更小,因此我们只需要再枚举比21大的值即可。也就是通过单调性,免去了很多不必要的枚举行为。
代码如下:
class Solution
{
public:vector<int> twoSum(vector<int>& price, int target){int left = 0;int right = price.size() - 1;while (left < right){if (price[left] + price[right] > target) //和比target大,right--right--;else if (price[left] + price[right] < target) //和比target小,left++left++;elsereturn { price[left], price[right] };}return { 0, 0 };}
};
LeetCode 11.盛水最多的容器
本题要求存储的最大水量,其实也就是两个下标之间的距离right - left与min(height[left], height[right])的乘积。
如果暴力枚举,那么就是枚举出每一对下标,然后求出最大面积,时间复杂度为 O ( N 2 ) O(N^{2}) O(N2)。
本题也可以使用双指针的算法,水量的值与right - left与min(height[left], height[right])两个变量正相关,如果我们利用两个指针向内枚举,那么right - left这个值是一直在减小的,也就是有一项有单调性。
对于这种,如果利用对撞指针下标向内枚举,对组成结果的某一项变量的影响是单调的,就可以考虑对撞指针。
假设我们已经在边界上定义好了left与right指针:
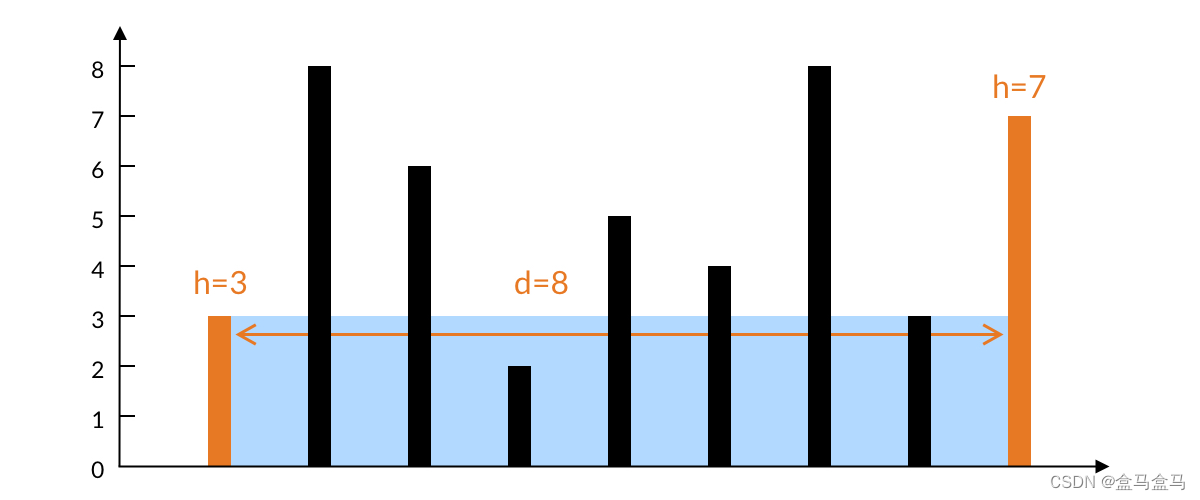
第一个问题就是,应该以什么规则进行向内移动指针?
移动的过程中,水的宽度的一直递减的,那么我们就要尽可能找到height高的元素,来拔高水量。
比如说当前的两个高度为3和7,由于水的高度取决于较低的那个元素,因此高度为7的指针无论怎么向内移动,水高度都不会超过3,而这个过程中宽度又是单调递减的,因此right指针向内移动,所有的结果都小于当前的水量。
比如这个情况:
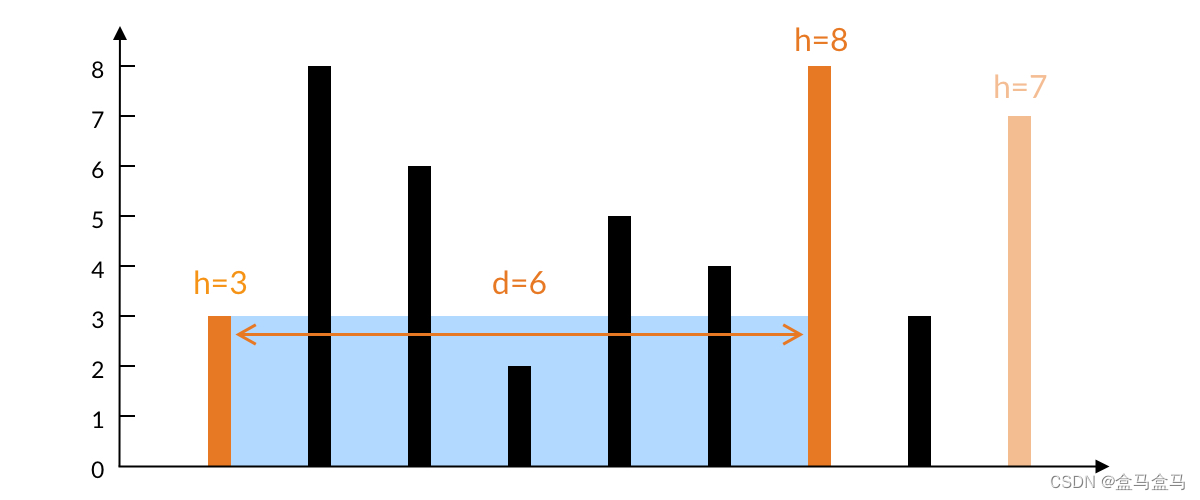
虽然right向内移动,找到了比7更大的元素,但是由于此时水高度取决于3,而且宽度还变小了,最后总水量没有变大。
因此每次都把比元素值较小的那个指针向内移动
代码如下:
class Solution
{
public:int maxArea(vector<int>& height){int left = 0;int right = height.size() - 1;int ret = -1;while (left <= right){int w = right - left;//宽度int h = min(height[left], height[right]);//高度ret = max(ret, w * h);//更新最大水量//每次都让较小的元素向内枚举if (height[left] > height[right])right--;elseleft++;}return ret;}
};
总结
双指针
- 数组划分使用双指针算法。
一般处理为[A区域][B区域]...[待处理]这样的格式,当新元素符合哪一个区域特性,就放到哪一个区域中。
快慢指针
- 循环问题,利用快慢指针来判断是否有循环。
相遇就是有环,如果fast走到结尾就是无环。
如果要找循环开始节点,一个指针从头开始走,一个指针从相遇点开始走,最后会在环入口相遇。
对撞指针
-
在一个有序区间中查找两个元素,计算得到固定值的题型,使用对撞指针。
-
如果利用对撞指针下标向内枚举,对组成结果的影响是单调的,就可以考虑对撞指针。
对撞指针的特点在于利用单调性减小搜索范围。
相关文章:

算法:双指针
算法:双指针 双指针快慢指针对撞指针总结 双指针 LeetCode 283.移动零 以上题目要求我们把所有0移动到数组的末尾,也就是说,我们要把数组转化为以下状态: [ 非0区域 ] [ 0区域 ] 像这种把一个数组划分为多个区域的题型࿰…...

MySQL一些特殊功能的索引(6/16)
特殊功能性索引 B-Tree索引: InnoDB的默认索引类型,适用于多种查询操作。 可以用于等值查询、范围查询和索引列的组合查询。 创建B-Tree索引的示例: CREATE INDEX index_name ON table_name (column1, column2);全文索引(FULLTEX…...
ES11-12
1-ES11-Promise.allSettled Promise.allSettled0)方法返回一个在所有给定的promise都已经fulfilled或rejected后的promise,并带有一个对象数组,每个对象表示对应的promise结果。 简单来说不管成功失败都会调用.then(),然后处理成功和失败的结果 const promises [ …...

【学习笔记】Vue3源码解析:第三部分-获取computed的值;实现computed
课程地址:【已完结】全网最详细Vue3源码解析!(一行行带你手写Vue3源码) 第三部分-获取computed的值;实现computed:(对应课程的第18-21节) 第22节:《获取computed的值》 …...
顺序表(C语言版)
前言:本篇文章我们来详细的讲解一下顺序的有关知识,这篇文章中博主会以C语言的方式实现顺序表。以及用顺序表去实现通讯录的代码操作。 目录 一.顺序表的概念 二.顺序表的分类 1.静态顺序表 三.动态顺序表的实现 1.顺序表的初始化 2.顺序表的尾插…...

Python高质量函数编写指南
The Ultimate Guide to Writing Functions 1.视频 https://www.youtube.com/watch?vyatgY4NpZXE 2.代码 https://github.com/ArjanCodes/2022-funcguide Python高质量函数编写指南 1. 一次做好一件事 from dataclasses import dataclass from datetime import datetimedatacl…...
)
探索Spring、Spring Boot和Spring Cloud的奇妙关系(二)
本系列文章简介: 在当今快节奏、高竞争的软件开发世界中,构建可靠、高效的应用程序是至关重要的。而Spring框架一直以来都是业界领先的Java开发框架之一,帮助开发者简化了复杂的任务,并提供了丰富的功能和强大的支持。 然而&#…...
Mysql的事务隔离级别以及事务的四大特性。
MySQL 的事务隔离级别是数据库管理系统中的一个重要概念,它决定了事务如何隔离和影响其他并发事务。MySQL 支持四种事务隔离级别,分别是:读未提交(READ UNCOMMITTED)、读已提交(READ COMMITTED)…...
人工智能_大模型023_AssistantsAPI_01_OpenAI助手的创建_API的调用_生命周期管理_对话服务创建---人工智能工作笔记0159
先来说一下一些问题: 尽量不要微调,很麻烦,而且效果需要自己不断的去测试. 如果文档中有图表,大量的图片去分析就不合适了. 是否用RAG搜索,这个可以这样来弄,首先去es库去搜能直接找到答案可以就不用去RAG检索了,也可以设置一个分,如果低于60分,那么就可以去进行RAG检索 微…...
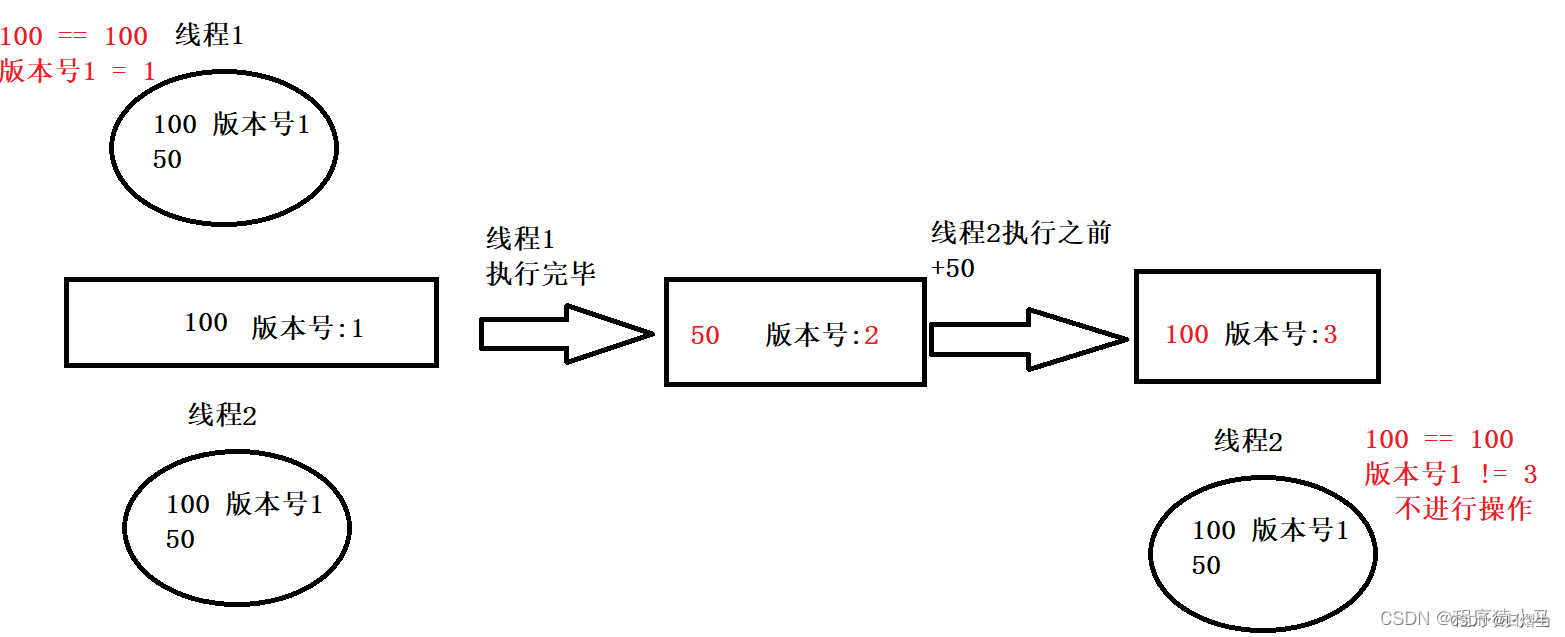
锁策略总结
锁策略 悲观锁和乐观锁 乐观锁和悲观锁不是具体类型的锁而是指两种不同的对待加锁的态度,这两个锁面对锁冲突的态度是相反的。 乐观锁:认为不存在很多的并发操作,因此不需要加锁。悲观锁:认为存在很多并发操作,因此需…...

蓝桥杯备考day2
1.1 map及其函数 map 提供一对一的数据处理能力,由于这个特性,它完成有可 能在我们处理一对一数据的时候,在编程上提供快速通道。map 中的第一 个值称为关键字(key),每个关键字只能在 map 中出现一次,第二个称为该 关…...
Mac电脑安装蚁剑
1: github 下载源码和加载器:https://github.com/AntSwordProjectAntSwordProject GitHubAntSwordProject has 12 repositories available. Follow their code on GitHub.https://github.com/AntSwordProject 以该图为主页面:antSword为源码…...

品牌百度百科词条创建多少钱?
百度百科作为国内最具权威和影响力的知识型平台,吸引了无数品牌和企业争相入驻。一个品牌的百度百科词条,不仅是对品牌形象的一种提升,更是增加品牌曝光度、提高品牌知名度的重要途径。品牌百度百科词条创建多少钱,这成为了许多企…...

Linux安装及管理程序
目录 一.Linux应用程序基础 1.应用程序与系统命令的关系 2.典型应用程序的目录结构 3.常见的Linux软件包封装类型 二.RPM 软件包管理工具 1.RPM 软件包管理器 Red-Hat Package Manger 2.RPM软件包 3.RPM命令 三.源代码编译安装 1. yum 软件包管理器: 配…...
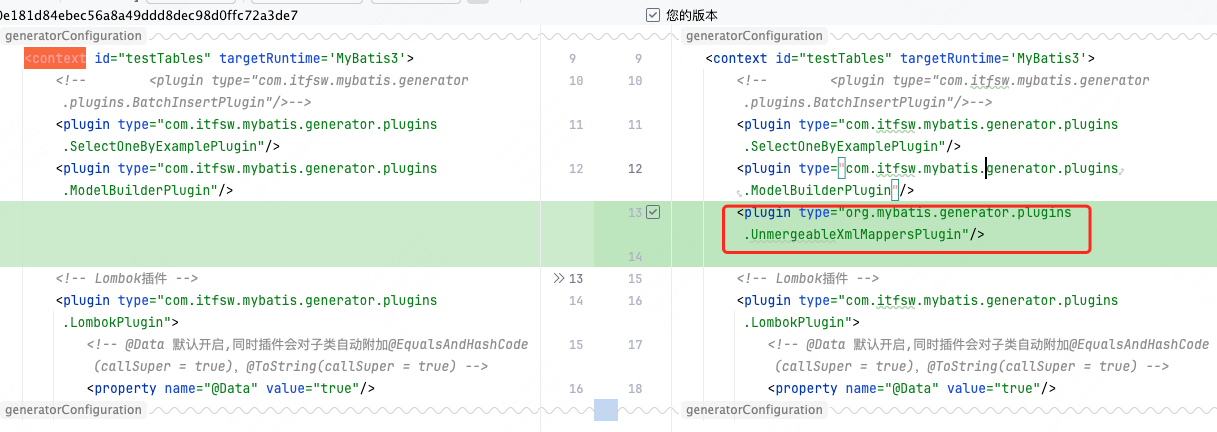
Mybatis generate xml 没有被覆盖
添加插件即可 <plugin type"org.mybatis.generator.plugins.UnmergeableXmlMappersPlugin"/>...
MercadoLibre(美客多)入仓预约系统操作流程-自动化约号(开篇)
目录 一、添加货件信息 二、输入货件信息 三、选择发货 四、填写交货日期 五、注意事项 MercadoLibre(美客多)于2021年10月18号上线了新预约入仓系统,在MercadoLibre美客多平台上,新入仓预约系统是一项非常重要的功能&#x…...

Unity TextMeshProUGUI 获取文本尺寸·大小
一般使用ContentSizeFitter组件自动变更大小 API 渲染前 Vector2 GetPreferredValues(string text)Vector2 GetPreferredValues(string text, float width, float height)Vector2 GetPreferredValues(float width, float height) 渲染后 Vector2 GetRenderedValues()Vector…...
Sonar下启动发生错误,elasticsearch启动错误
Download | SonarQube | Sonar (sonarsource.com) 1.首先我的sonar版本为 10.4.1 ,java版本为17 2.sonar启动需要数据库,我先安装了mysql, 但是目前sonar从7.9开始不支持mysql,且java版本要最少11,推荐使用java17 3.安装postsql,创建sonar数据库 4.启…...

Git常用命令以及异常信息汇总
常用命令: 查看本地分支: git branch 创建一个新仓库 git clone 仓库地址xxxxx cd 目标目录 git switch -c main touch README.md git add README.md git commit -m "add README" git push -u origin main 推送现有文件夹 cd 目标目录 git in…...

解释Python中的RESTful API设计和实现
解释Python中的RESTful API设计和实现 RESTful API,即符合REST(Representational State Transfer,表述性状态转移)架构风格的Web服务接口,已成为现代Web应用程序通信的标准。Python作为一种灵活且强大的编程语言&…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...

高保真组件库:开关
一:制作关状态 拖入一个矩形作为关闭的底色:44 x 22,填充灰色CCCCCC,圆角23,边框宽度0,文本为”关“,右对齐,边距2,2,6,2,文本颜色白色FFFFFF。 拖拽一个椭圆,尺寸18 x 18,边框为0。3. 全选转为动态面板状态1命名为”关“。 二:制作开状态 复制关状态并命名为”开…...
