趣话最大割问题:花果山之群猴博弈

内容来源:量子前哨(ID:Qforepost)
编辑丨浪味仙 排版丨 沛贤
深度好文:3000字丨15分钟阅读
趋利避害,是所有生物遵循的自然法则,人类也不例外。
举个例子,假如你是某生鲜平台的配送员,载着满满一电瓶车货物,要将其配送至片区内多个住户。
在多劳多得的规则下,要想多赚点配送费,你就不得不合理规划配送路径,尽量少走回头路,以最快速度完成配送,最终返回站点。
如果是你,会怎样规划路线?
都说世界是数学的,生活中诸如此类的困扰,都可以归为一类,叫做组合优化问题:在有限个可能解的集合中,找出最优解。
如何顺应人类趋利避害的天性,做出利益最大化的抉择?还得是魔法打败魔法。
现在可以请出今天的主角最大割问题 (Max-Cut Problem):一种能够帮我们合理规划复杂组合关系的数学问题。
01
何为最大割问题?
对绝大多数不熟悉数学或编程的读者来说,一看「最大割」这仨字,必然断定它是个既枯燥又难懂的学术名词。
事实上,它蛮有趣、也并不难懂。
在解释概念之前,各位不妨先听个故事,名字叫做《该死,美猴王那纷纷扰扰的花果山》。
话说,花果山上有只石猴,獐鹿为友,猕猿为亲,携众猴入驻花果山后,被拥立为美猴王。
可美猴王也有烦恼:正所谓猴性顽劣,目之所及,众猴抢盆夺碗,占灶争床,眼瞅花果山恐再无宁时,真真是头疼。
于是,美猴王体内趋利避害的远古基因开始觉醒:怎样才能让花果山最大程度地保持和平?
不如取消原有大杂居,试试分区管理?可碍于辖区内面积有限,只有两座山头可分,又该怎么分呢?
美猴王开始了一场思想实验。
情况 1:假设有 2 只见面就掐架的猴,外加两座猴山;
这种情况下,总共有 4 种分区方案。

那么,在这 4 种方案中,哪种最能维持整体和平呢?
我们将这 2 只猴看作一组关系,通过辅助线(实线代表小猴之间见面就掐的矛盾)来观察。
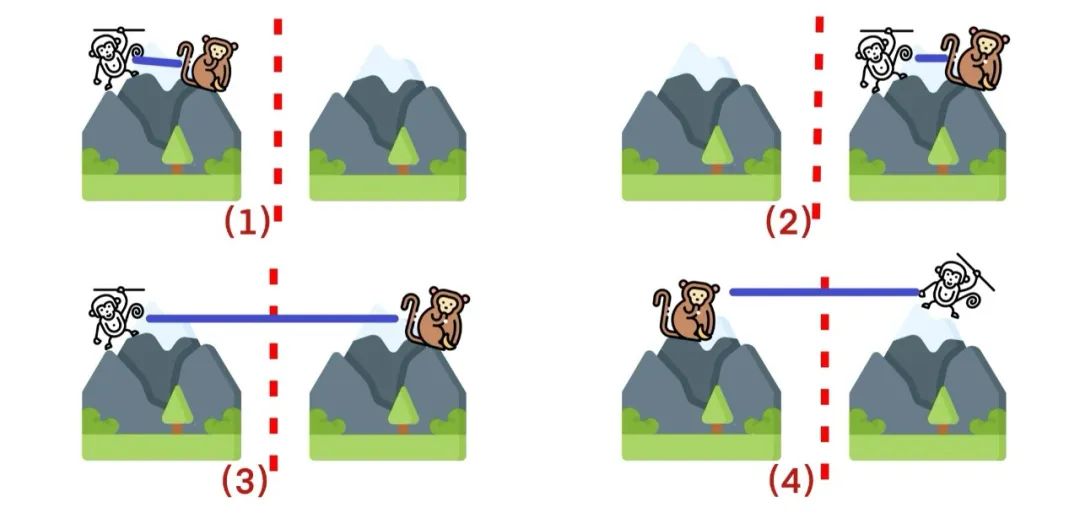
可以看到,切割这组猴的关系线时,图 1 和 2 没有线被切断,图 3 和 4 切断线的数量为 1。
这意味着,此种情况下,切断 1 条关系线的方案,可以维持花果山和平。
情况 2:假设有 4 只彼此都不服的猴,外加两座猴山;
这种情况下,总共有 16 种分区方案。(出于篇幅考虑,下面仅展示 4 种。)

在这些方案中,哪种最能维持花果山和平呢?我们依然将 4 只猴看作一组关系,通过辅助线来观察。
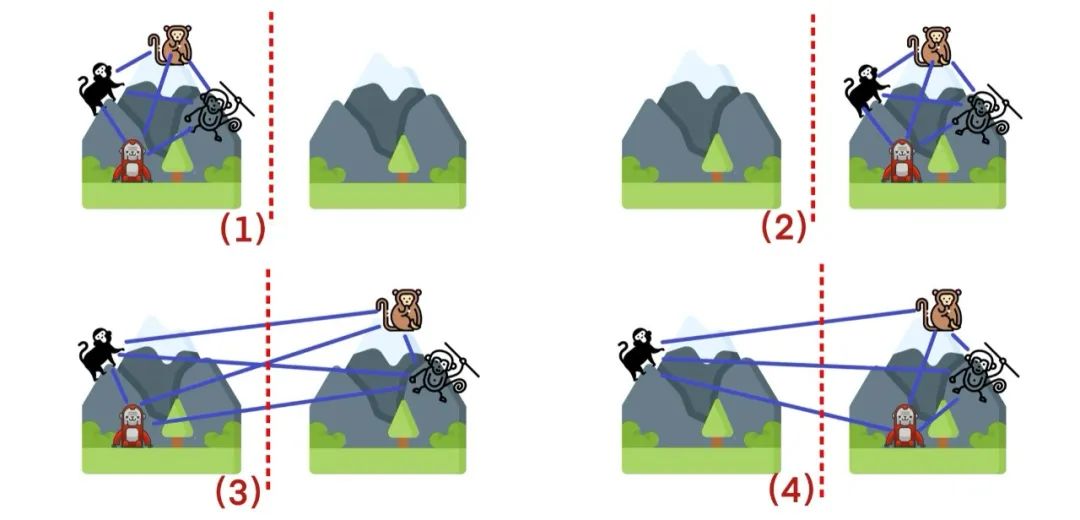
可以看到,在切割这组包含 4 只猴的关系线时,图 3 被切断的线最多,数量为 4。
也就是说,在此种情况下,切断 4 条关系线的方案,最能维持花果山和平。
情况 3:假设有 5 只猴 (有些猴之间有矛盾,有些猴之间没有,仍用连线表示),外加两座猴山;
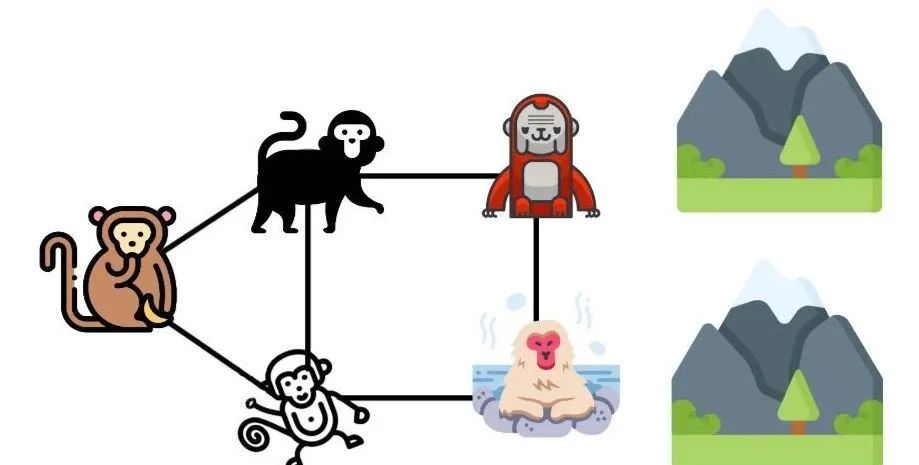
这种情况下,怎样将这 5 只猴合理分开呢?感兴趣的读者可以找张纸画一画。
根据前两种假设我们可知,最能维持花果山和平的方案,被切断的关系线数量一定最多。
放在此种假设中,最优方案切断的数量线为 5 条 (尽管右侧山上其中两只猴也有矛盾,但这种分割法已经是最优解了)。
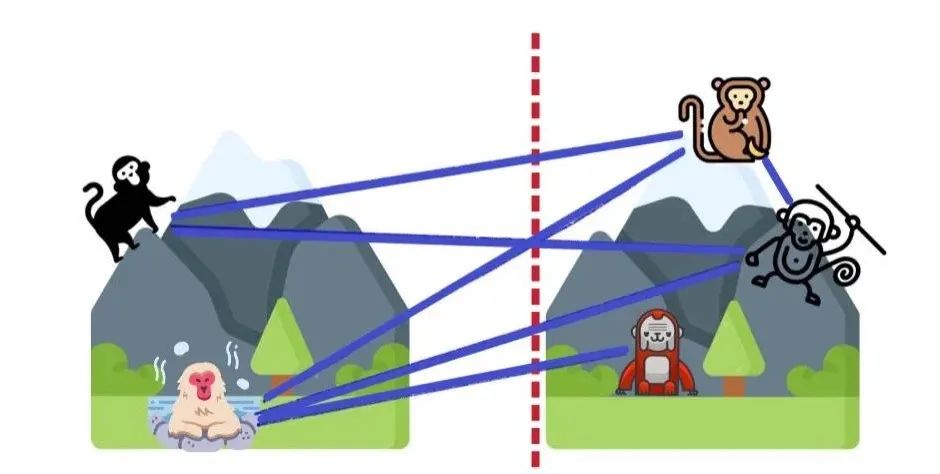
换成平面切割视图,则是这样:
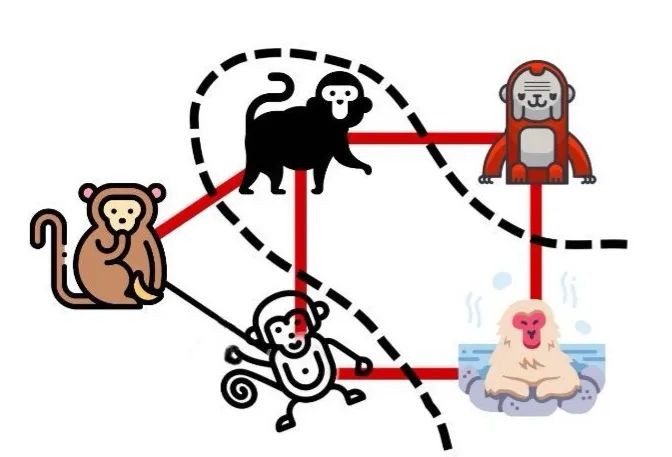
OK,故事听到这里,恭喜,你已经会求解最大割问题了。
所谓最大割 Max-Cut 问题,就是求一种分割方法:给定一张无向图,将所有顶点分割成两群,使得同时被切断的边数量最大。
故事中,猴子对应图中的顶点,俩猴之间的矛盾则对应边。
但你有没有留意到,在前面的假设中,我们默认猴子间的矛盾值都相同,倘若不同呢?比如猴甲与猴乙之间有杀父之仇夺妻之恨,见面肯定以死相拼;但猴甲和猴丁只是因为昨天分桃时猴丁插了个队,见面顶多会呸一声。
实际生活中,在矛盾值有高有低的情况下,我们还需要优先把一言不合便要掐个你死我活的隔开。
当每条边都有一个权重系数时,分割目标函数的思路就会发生变化,从使被切断的边数量最大,变为使切割边的总权重之和最大。这种情况较刚才的假设更为复杂,我们称其为加权最大割问题。
到此,最大割问题的描述就讲完了,这种轻松涨知识的感觉是不是还不赖?诶等等,各位先别急着开香槟。
这个世界,远比想象中复杂。
02
最大割问题为何难解?
刚才是谁按下了各位开香槟的手?哦对,是我,但我是有原因的。
不知各位读者有没有留意到,刚才发生在美猴王故事中的几种假设,我们都能靠手工画图完成。
从专业角度来说,我们用的是穷举法。
穷举法,是指根据题目给定的约束条件,从可能的集合中一一列举出问题答案,再依次判定:令命题成立者,即为解。
一言以蔽之:大力出奇迹。
倘若不是 2、4、5 只猴子,而是 10、50、100、甚至直接捅穿猴子窝成千上万只猴子,我们还能用穷举法计算出结果吗?
不能。
这里存在一个被称为「计算复杂度」的巨大挑战。
在计算机科学中,一个问题的计算复杂度,就是看运行这个算法所需要的资源量,特别是时间 (CPU 占用时间) 和空间 (内存占用时间)。如果问题的计算复杂度比较高,当问题的变量数增大时,需要筛选的备选答案数量(我们称之为“解空间”)就可能以极快的速度增加。
当需要筛选的可能答案数量过于巨大时,哪怕派出当今运行速度最快的计算机也极难完成,因为计算机需要太多时间来验证所有方案的可能性。
这时,局面就会开始失控。
比如旅行商问题:3 句话就能描述清楚,但很小的变量数就能形成一个极其庞大的解空间,从而使得用计算机去穷举的“蛮力解法”耗时变得极长。
旅行商问题:一个商品推销员要遍访多个城市,期间所有城市不能重复经过,最后回到出发城市。
他该如何规划最短路径?
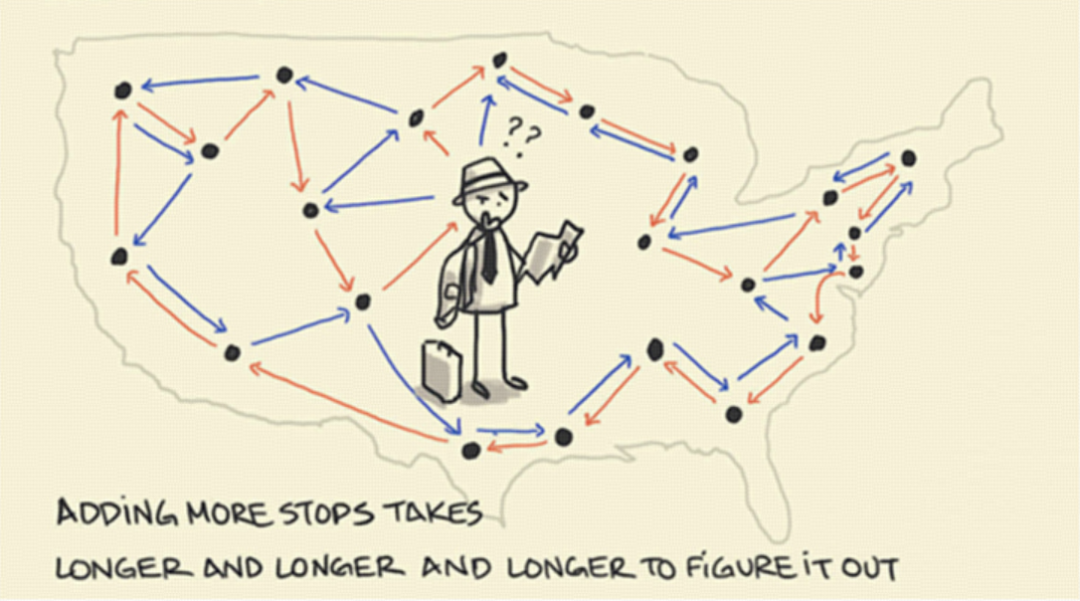
旅行商问题的描述看上去很简单吧?直觉上是不是很好求解?
但是!从数学角度来看,它的挑战在于,随着城市数的增加,求解的计算量会呈“阶乘级”上升。
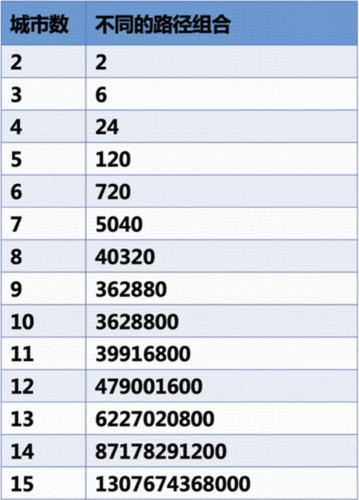
大家能一眼就念出 15 个城市可能存在的路径组合数量吗?
数学上,我们用一个非常形象的词来描述这种现象,叫做「组合爆炸」:变量 (城市数) 只是增加了一点点,解空间的可能性就快速增长成一个极其庞大的规模。
回到花果山的故事中,当猴子数量、矛盾关系数量持续增加时,美猴王所要考虑的分割方案的数量同样会呈阶乘级增长,再也没法用简单的“画图穷举”的方法去求解了。
至此,我们可以对最大割问题做个简单总结:
1) 作为组合优化问题的一种,随着问题规模的增加,可能的解决方案数量会呈阶乘级增长;(采用穷举法,几乎不可能在可接受的时间内找到全局最优解。)
2) 当解决方案数量呈阶乘级增长时,求解组合优化问题的难度,将大大超出经典计算机的能力范围。
03
最大割问题有何现实意义?
你或许会想,尽管明白了什么是最大割问题,但它有什么用呢?现实生活中哪儿有那么多调皮的小猴需要我去调度?
诶,千万别小瞧了它。
德国当代著名作家丹尼尔·凯曼说过:“数学并不会使人脱离现实世界,恰恰相反,数学牵引着现实,让人更加接近现实,让现实更加清晰。”
最大割问题,就是这句话的优雅诠释。
远的不提,咱就拿自动驾驶来说,汽车要想安全地自行驾驶,必须得能感知周围环境,除了要能“认清”车辆行人的行动轨迹,还得能分清路面移动的物体是野猫还是塑料袋,从而精准避障。
但汽车的“眼睛”是摄像头和雷达,这些感官设备带给它的只是一堆一堆的 01 数据,还需要它的大脑去“识别”这些数据所代表的“具体含义”。
以摄像头为例,它所获取的是一帧帧平面二维图片,图片则由一个个不同色值的像素点构成。至于哪些像素点应该被归纳为物体 A,哪些像素点应该被归纳为物体 B,就需要自动驾驶的“大脑”去计算和识别。
要实现这一点,离不开图像分割技术,也就是通过将图像划分成互不相交的区域,实现物体分离,再一一将这些物体识别成不同的对象,进而去判断这些对象会不会动、会怎么动,与汽车自身的运动会不会产生碰撞等,这才能让汽车“看清楚路”。
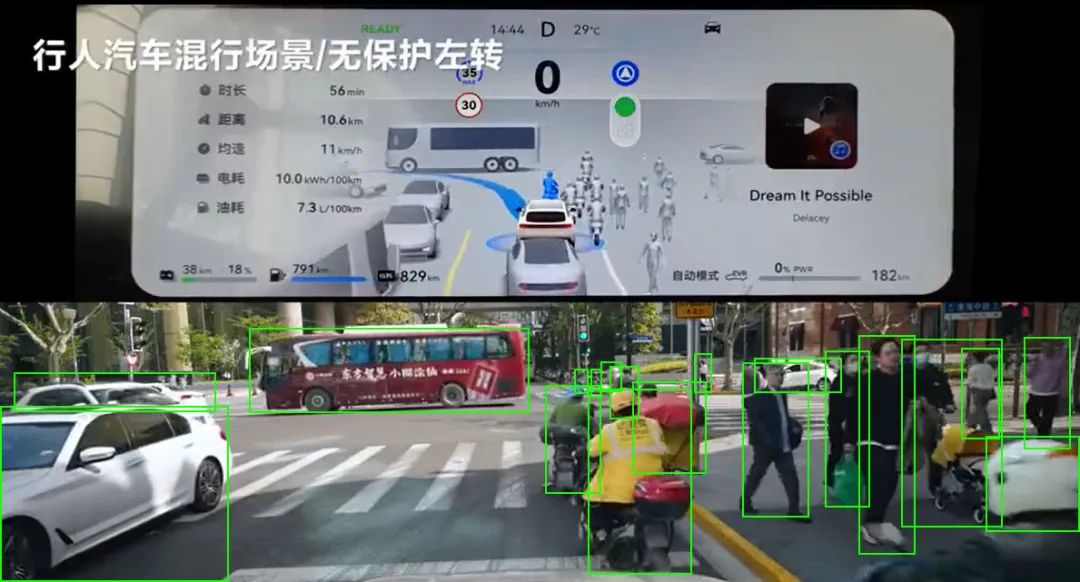
最大割问题可以帮助完成图像分割。
汽车周身摄像头拍摄到的画面,可以将其映射为带权无向图,像素视为图中节点。这样一来,图像分割问题就转化成了图的顶点划分问题,利用最小剪切准则,得到图像的最佳分割,汽车就能“看见”路况,进而科学决策,做到安全驾驶。
而这只是最大割问题应用的冰山一角,事实上,它的应用或变体遍布整个商业领域,是构成我们数字社会非常重要的算法基础。
1、金融:动态投资组合优化、欺诈检测、信用评估、客户划分;
2、通信:MIMO 波束选择及资源分配;
3、设计:电路板优化设计;
4、能源:主动配电网的路径优化;
5、交通:大规模交通流路径规划;
6、物流:包裹配送优化、物流仓布局;
7、医疗:疾病诊断与医学图像分析;
8、生物制药:小分子对接筛选;
9、工业制造:生产流程优化、整体质量控制流程优化;
10、电子商务:产品推荐、库存管理;
... ...
“世界是数学的。”美国思想家爱默生说:“在它巨大流畅的曲线中没有意外。”
要我说,意外还是有的。
你瞧,在如何发现世界中的数学、如何用好数学等方面,都藏着意外。
相关文章:

趣话最大割问题:花果山之群猴博弈
内容来源:量子前哨(ID:Qforepost) 编辑丨浪味仙 排版丨 沛贤 深度好文:3000字丨15分钟阅读 趋利避害,是所有生物遵循的自然法则,人类也不例外。 举个例子,假如你是某生鲜平台的配…...

上周面试了一个大模型算法岗的女生,有点崩溃。。。
节前,我们星球组织了一场算法岗技术&面试讨论会,邀请了一些互联网大厂朋友、参加社招和校招面试的同学,针对算法岗技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何准备、面试常考点分享等热门话题进行了深入的讨论。 汇总…...

AI系列:大语言模型的function calling
目录 大语言模型(LLM) 的function calling实验:OpenAI之function calling序列图:function calling如何工作详情: 对话内容参考代码 后续: 使用LangChain实现function calling参考 大语言模型(LLM) 的function calling 大语言模型(LLM)可以使用自然语言与…...

conda 创建、激活、退出、删除虚拟环境
一、conda 本地环境常用操作 #获取版本号 conda --version 或 conda -V #检查更新当前conda conda update conda #查看当前存在哪些虚拟环境 conda env list 或 conda info -e #查看--安装--更新--删除包 conda list: conda search package_name# 查询包 cond…...

【Entity Framework】聊一聊EF中继承关系
【Entity Framework】聊一聊EF中继承关系 文章目录 【Entity Framework】聊一聊EF中继承关系一、概述二、实体类型层次结构映射三、每个层次结构一张表和鉴别器配置四、共享列五、每个类型一张表配置六、每个具体类型一张表配置七、TPC数据库架构八、总结 一、概述 Entity Fra…...
curaengine编译源码之libarcus编译记录
libArcus的编译(成功安装) This library contains C code and Python3 bindings for creating a socket in a thread and using this socket to send and receive messages based on the Protocol Buffers library. It is designed to facilitate the c…...
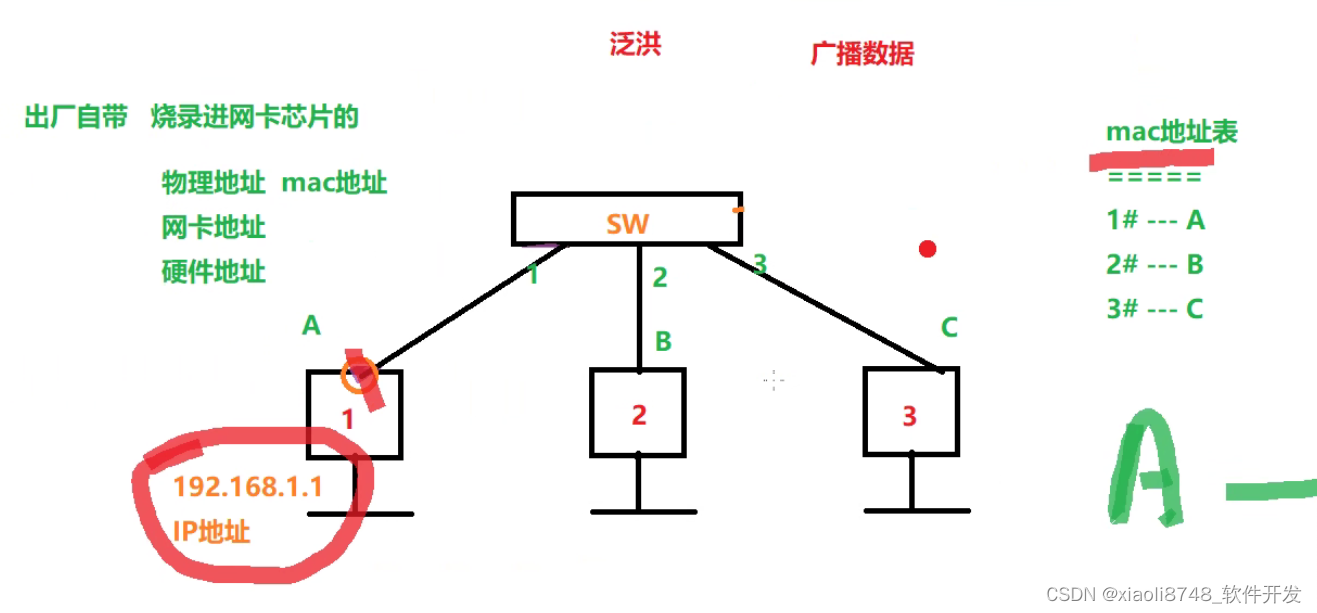
运用OSI模型提升排错能力
1. OSI模型有什么实际的应用价值? 2. 二层和三层网络的区别和应用; 3. 如何通过OSI模型提升组网排错能力? -- OSI - 开放式系统互联 - 一个互联标准 - 从软件和硬件 定义标准 - 不同厂商的设备 研发的技术 - 具备兼容性 -- O…...
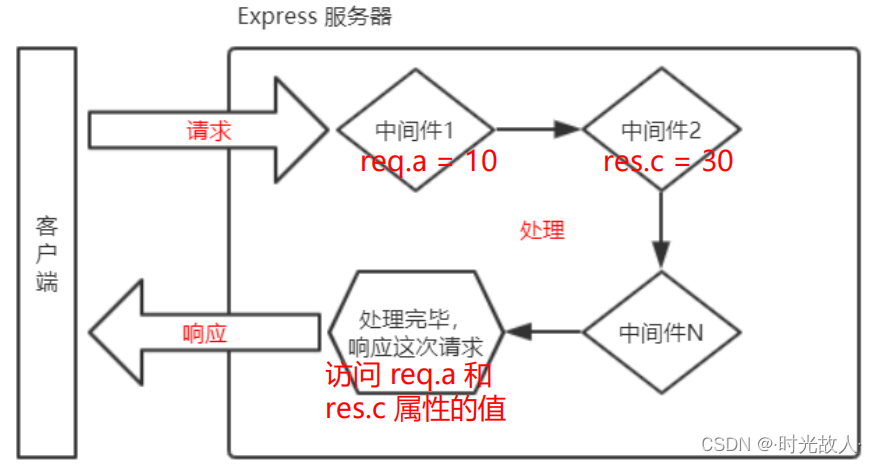
【Node.js】Express学习笔记(黑马)
目录 初识 ExpressExpress 简介Express 的基本使用托管静态资源nodemon Express 路由路由的概念路由的使用 Express 中间件中间件的概念Express 中间件的初体验中间件的分类 初识 Express Express 简介 什么是 Express? 官方给出的概念:Express 是基于…...
Linux系统部署Tale个人博客并发布到公网访问
目录 ⛳️推荐 前言 1. Tale网站搭建 1.1 检查本地环境 1.2 部署Tale个人博客系统 1.3 启动Tale服务 1.4 访问博客地址 2. Linux安装Cpolar内网穿透 3. 创建Tale博客公网地址 4. 使用公网地址访问Tale ⛳️推荐 前些天发现了一个巨牛的人工智能学习网站,通…...
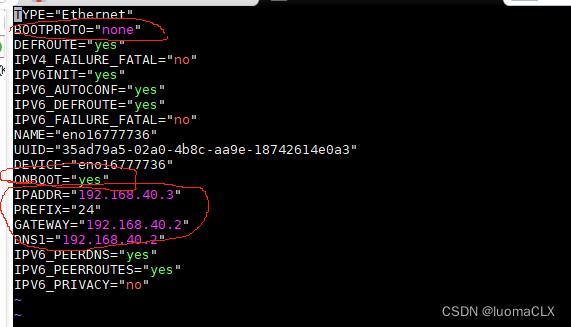
CentOS7里ifcfg-eth0文件不存在解决方案/Centos7修改网络IP解决方案
Centos7网络IP地址手动设置 1、centos7没有ifcfg-eth0,我的centos7也没有其他博客说的什么ifcfg-ens33、ifcfg-ens32,然后我打开了我这里的ifcfg-eno***,结果发现就是centos6里的ifcfg-eth0里的网络配置。2、vim ifcfg-eno***(按t…...

go第三方库go.uber.org介绍
Uber 是一家美国硅谷的科技公司,也是 Go 语言的早期 adopter。其开源了很多 golang 项目,诸如被 Gopher 圈熟知的 zap、jaeger 等。2018 年年末 Uber 将内部的 Go 风格规范 开源到 GitHub,经过一年的积累和更新,该规范已经初具规模…...
Oracle 正则表达式
一、Oracle 正则表达式相关函数 (1) regexp_like :同 like 功能相似(模糊 匹配) (2) regexp_instr :同 instr 功能相似(返回字符所在 下标) (3) regexp_substr : 同 substr 功能相似&…...

MongoDB聚合运算符:$rand
MongoDB聚合运算符:$rand 文章目录 MongoDB聚合运算符:$rand语法举例生成随机数据点从集合中随机选择条目 $rand聚合运算符用于返回一个0~1之间的随机浮点数。 语法 { $rand: {} }$rand运算符不需要任何参数。每次调用$rand都会返回一个小数点后最多17位…...
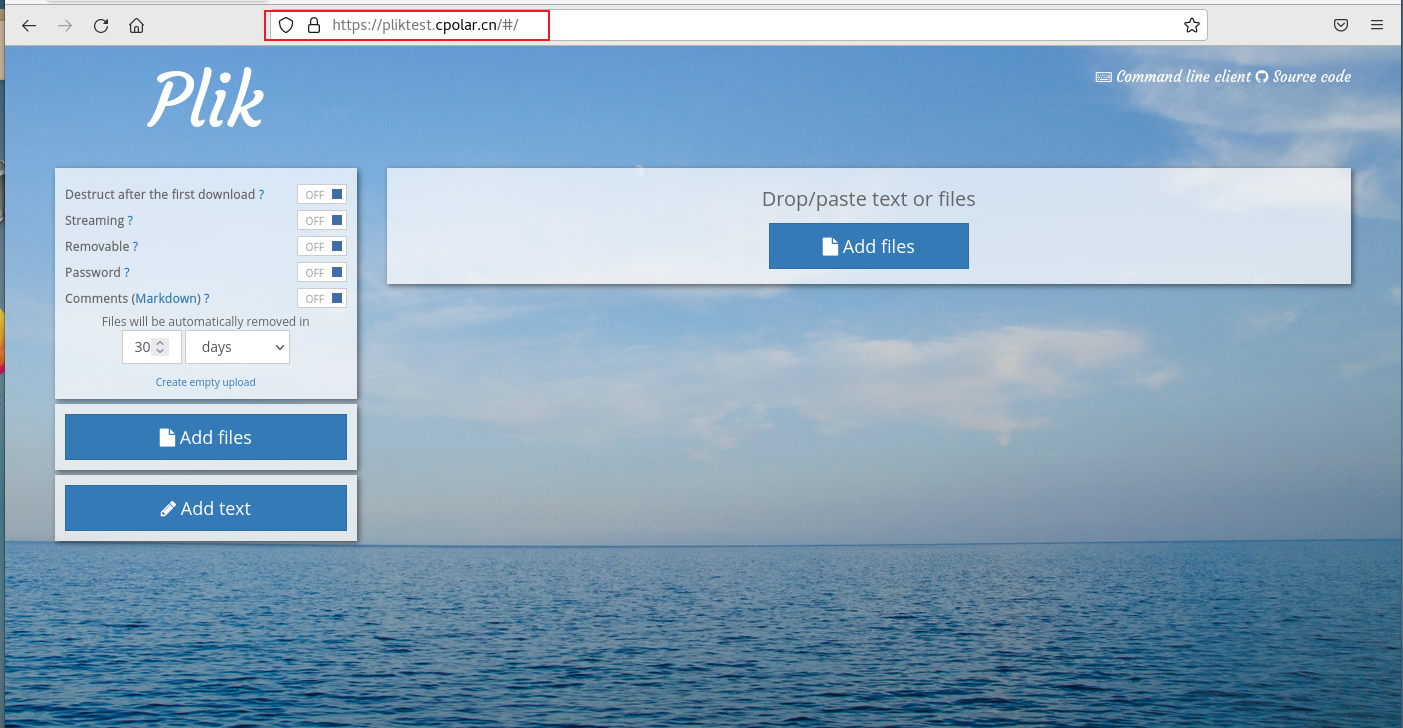
如何在Linux通过docker搭建Plik文件系统并实现无公网IP管理内网文件
文章目录 1. Docker部署Plik2. 本地访问Plik3. Linux安装Cpolar4. 配置Plik公网地址5. 远程访问Plik6. 固定Plik公网地址7. 固定地址访问Plik 本文介绍如何使用Linux docker方式快速安装Plik并且结合Cpolar内网穿透工具实现远程访问,实现随时随地在任意设备上传或者…...
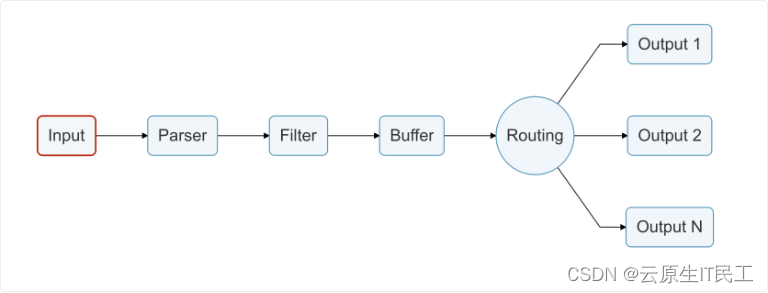
k8s部署efk
环境简介: kubernetes: v1.22.2 helm: v3.12.0 elasticsearch: 8.8.0 chart包:19.10.0 fluentd: 1.16.2 chart包: 5.9.4 kibana: 8.2.2 chart包:10.1.9 整体架构图: 一、Elasticsearch安装…...

AI模型大PK
🤖AI模型大PK!免费测试GPT-4等36款顶级聊天机器人 近年来,大型语言模型(LLM)的发展日新月异,各大科技巨头和研究机构纷纷推出了自己的聊天机器人。那么,如何才能知道哪个模型更强大、更智能呢&…...
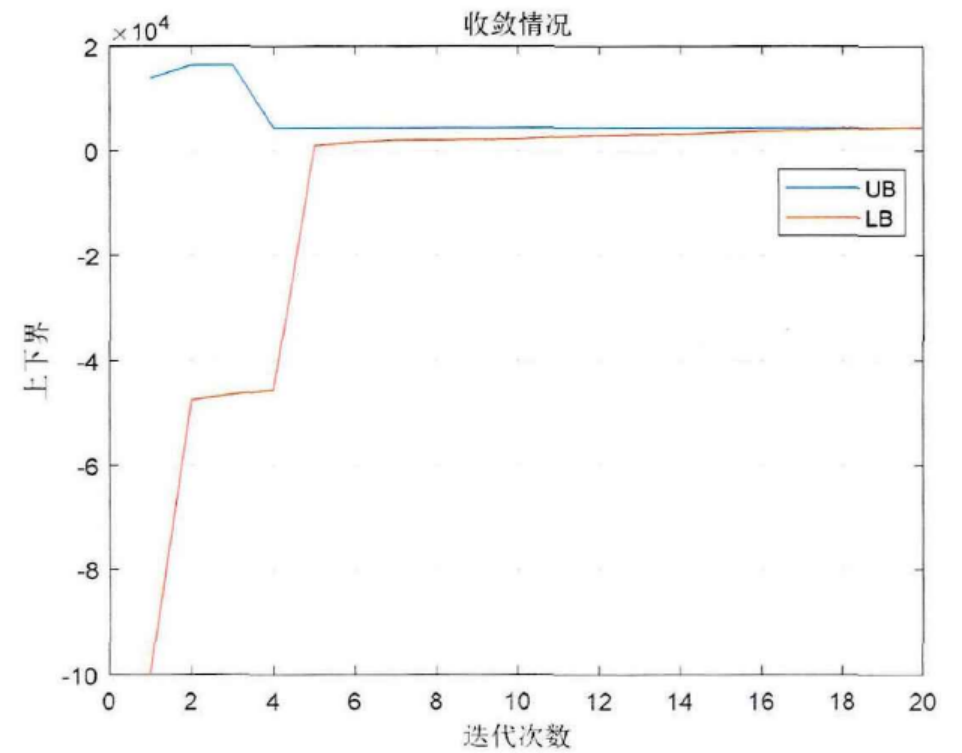
Matlab|基于广义Benders分解法的综合能源系统优化规划
目录 1 主要内容 广义benders分解法流程图: 优化目标: 约束条件: 2 部分代码 3 程序结果 4 下载链接 1 主要内容 该程序复现文章《综合能源系统协同运行策略与规划研究》第四章内容基于广义Benders分解法的综合能源系统优化规划&…...
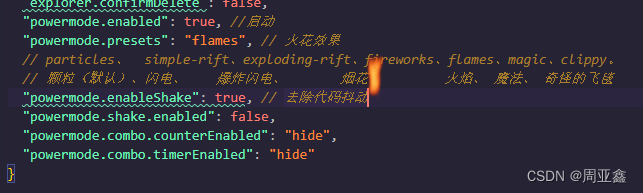
vscode 打代码光标特效
vscode 打代码光标特效 在设置里面找到settings 进入之后在代码最下方加入此代码 "explorer.confirmDelete": false,"powermode.enabled": true, //启动"powermode.presets": "fireworks", // 火花效果// particles、 simple-rift、e…...

【代码随想录算法训练营第四十八天 | LeetCode198.打家劫舍、213.打家劫舍II、337.打家劫舍III】
代码随想录算法训练营第四十八天 | LeetCode198.打家劫舍、213.打家劫舍II、337.打家劫舍III 一、198.打家劫舍 解题代码C: class Solution { public:int rob(vector<int>& nums) {if (nums.size() 0) return 0;if (nums.size() 1) return nums[0];ve…...
蓝桥杯 — —灵能传输
灵能传输 友情链接:灵能传输 题目: 输入样例: 3 3 5 -2 3 4 0 0 0 0 3 1 2 3输出样例: 3 0 3思路: 题目大意:给出一个数组,每次选择数组中的一个数(要求不能是第一个数与最后一个…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
