【动态规划】
动态规划1
- 引言
- 题目
- 509. 斐波那契数
- 70. 爬楼梯
- 746. 使用最小花费爬楼梯
- 小结
- 53. 最大子数组和
- 结语
引言
蓝桥杯快开始了啊,自从报名后还没认真学过算法有`(>﹏<)′,临时抱一下佛脚,一起学学算法。
题目
509. 斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
链接: link
相信这题大家都能闭着眼睛都能写出来了。
这是一个最基础的递推题目
递推公式为**F(n) = F(n - 1) + F(n - 2)**
1.定义一个数组arr[n+1], 用来记录n位置的斐波那契数值
2.定义一个循环变量i 然后进行循环F(i) = F(i - 1) + F(i - 2)
3.返回arr[n]
代码:
int fib(int n){if(n<=1){return n;}else{int arr[n+1];arr[0]=0;arr[1]=1;for(int i=2;i<=n;i++){arr[i]=arr[i-1]+arr[i-2];}return arr[n];}
}
70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
链接: 爬楼梯
这道题就是斐波那契数列的简单应用,只是在斐波那契数列是套了一层外套
1.当你在n阶楼梯时
2.只能由n-1阶时走一步或者在n-2阶时走两步
3.所以爬到n阶的方法总数等于爬n-1阶时的方法数加上爬到n-2阶的方法数
也就是F(n)=F(n-1)+F(n-2)(状态转移方程)
代码:
int climbStairs(int n){int arr[46]={1,1};for(int i=2;i<=n;i++){arr[i]=arr[i-1]+arr[i-2];}return arr[n];
}
746. 使用最小花费爬楼梯
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20]
输出:15
解释:你将从下标为 1 的台阶开始。
- 支付 15 ,向上爬两个台阶,到达楼梯顶部。 总花费为 15 。
示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1]
输出:6
解释:你将从下标为 0 的台阶开始。
- 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
- 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
- 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
- 支付 1 ,向上爬一个台阶,到达楼梯顶部。 总花费为 6 。
提示:
2 <= cost.length <= 1000
0 <= cost[i] <= 999
链接: 使用最小花费爬楼梯
这题和之前的爬楼梯很相似,只是从求方案数到求最小值。
求解思路:
当你在 n 阶楼梯时
只能由 n-1 阶时走一步或者在 n-2 阶时走两步
当选择走 n-1 其花费也是走到 n-1 步时的最小花费加上走这一步的花费
n-2 其花费也是走到 n-2 步时的最小花费加上走这一步的花费
arr[n]值就是两者之间的最小值
定义一个数组arr[1001],用来存储走到n阶楼梯时的最小花费
我们可以得出状态转移方程为
arr[i]=min(arr[i-1]+cost[i-1],arr[i-2]+cost[i-2])
代码:
int min(int a,int b)
{if(a>b)return b;return a;
}int minCostClimbingStairs(int* cost, int costSize){int arr[1001]={0,0};for(int i=2;i<=costSize;i++){arr[i]=min(arr[i-1]+cost[i-1],arr[i-2]+cost[i-2]); }return arr[costSize];
}
小结
从上述三题可以看出动态规划的大致流程
1.设计状态
2.写出状态转移方程
3.设定初始状态
4.执行状态转移
5.返回最终的解
接下来我们在看一个题
53. 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
题解:
定义一个dp[100001]数组,用于储存以nums[n]为结尾的子数组的和的最大值。
然后根据题意可知,dp[n]的值有两种情况:
第一种:
- 当dp[n-1]<=0时,
- 表示的是以nums[n-1]结尾的所有子数组的最大值小于0,
- 此时dp[n]的值应该是arr[n]的值,因为一个数加上一个小于0的数总比原数小。
第二种:
- 当dp[n-1]>0时,
- dp[n]的值应该取dp[n-1]和dp[n-1]+nums[n]这两数中的最大值
可得状态转移方程为dp[n]=max(dp[n-1]+nums[n],nums[n])
设置初始状态 dp[0]=arr[0]
代码:
int max(int i,int j)
{if(i>j)return i;return j;
}int maxSubArray(int* nums, int numsSize){int dp[100001]={};dp[0]=nums[0];int maxval=nums[0];for(int n=1;n<numsSize;n++){dp[n]=max(dp[n-1]+nums[n],nums[n]);maxval=max(maxval,dp[n]);}return maxval;
}
结语
本期动态规划就到这了
我是Tom-猫
如果觉得有帮助的话,记得
一键三连哦ヾ(≧▽≦*)o。

相关文章:

【动态规划】
动态规划1引言题目509. 斐波那契数70. 爬楼梯746. 使用最小花费爬楼梯小结53. 最大子数组和结语引言 蓝桥杯快开始了啊,自从报名后还没认真学过算法有(>﹏<)′,临时抱一下佛脚,一起学学算法。 题目 509. 斐波那契数 斐波那契数 &am…...

秒懂算法 | DP概述和常见DP面试题
动态(DP)是一种算法技术,它将大问题分解为更简单的子问题,对整体问题的最优解决方案取决于子问题的最优解决方案。本篇内容介绍了DP的概念和基本操作;DP的设计、方程推导、记忆化编码、递推编码、滚动数组以及常见的DP面试题。 01、DP概述 1. DP问题的特征 下面以斐波那…...
)
【C++提高编程】C++全栈体系(二十五)
C提高编程 第四章 STL- 函数对象 一、函数对象 1. 函数对象概念 概念: 重载函数调用操作符的类,其对象常称为函数对象函数对象使用重载的()时,行为类似函数调用,也叫仿函数 本质: 函数对象(仿函数)是一个类&…...

【云原生】k8s核心技术—集群安全机制 Ingress Helm 持久化存储-20230222
文章目录一、k8s集群安全机制1. 概述2. RBAC——基于角色的访问控制二、Ingress三、Helm1. 引入2. 使用功能Helm可以解决哪些问题3. 介绍4. 3个重要概念5. helm 版本变化6. helm安装及配置仓库7. 使用helm快速部署应用8. 自己创建chart9. 实现yaml高效复用四、持久化存储1.nfs—…...
【Linux】实现简易的Shell命令行解释器
大家好我是沐曦希💕 文章目录一、前言二、准备工作1.输出提示符2.输入和获取命令3.shell运行原理4.内建命令5.替换三、整体代码一、前言 前面学到了进程创建,进程终止,进程等待,进程替换,那么通过这些来制作一个简易的…...

再获认可!腾讯安全NDR获Forrester权威推荐
近日,国际权威研究机构Forrester发布最新研究报告《The Network Analysis And Visibility Landscape, Q1 2023》(以下简称“NAV报告”),从网络分析和可视化(NAV)厂商规模、产品功能、市场占有率及重点案例等…...
代码审计之旅之百家CMS
前言 之前审计的CMS大多是利用工具,即Seay昆仑镜联动扫描出漏洞点,而后进行审计。感觉自己的能力仍与零无异,因此本次审计CMS绝大多数使用手动探测,即通过搜索危险函数的方式进行漏洞寻找,以此来提升审计能力…...
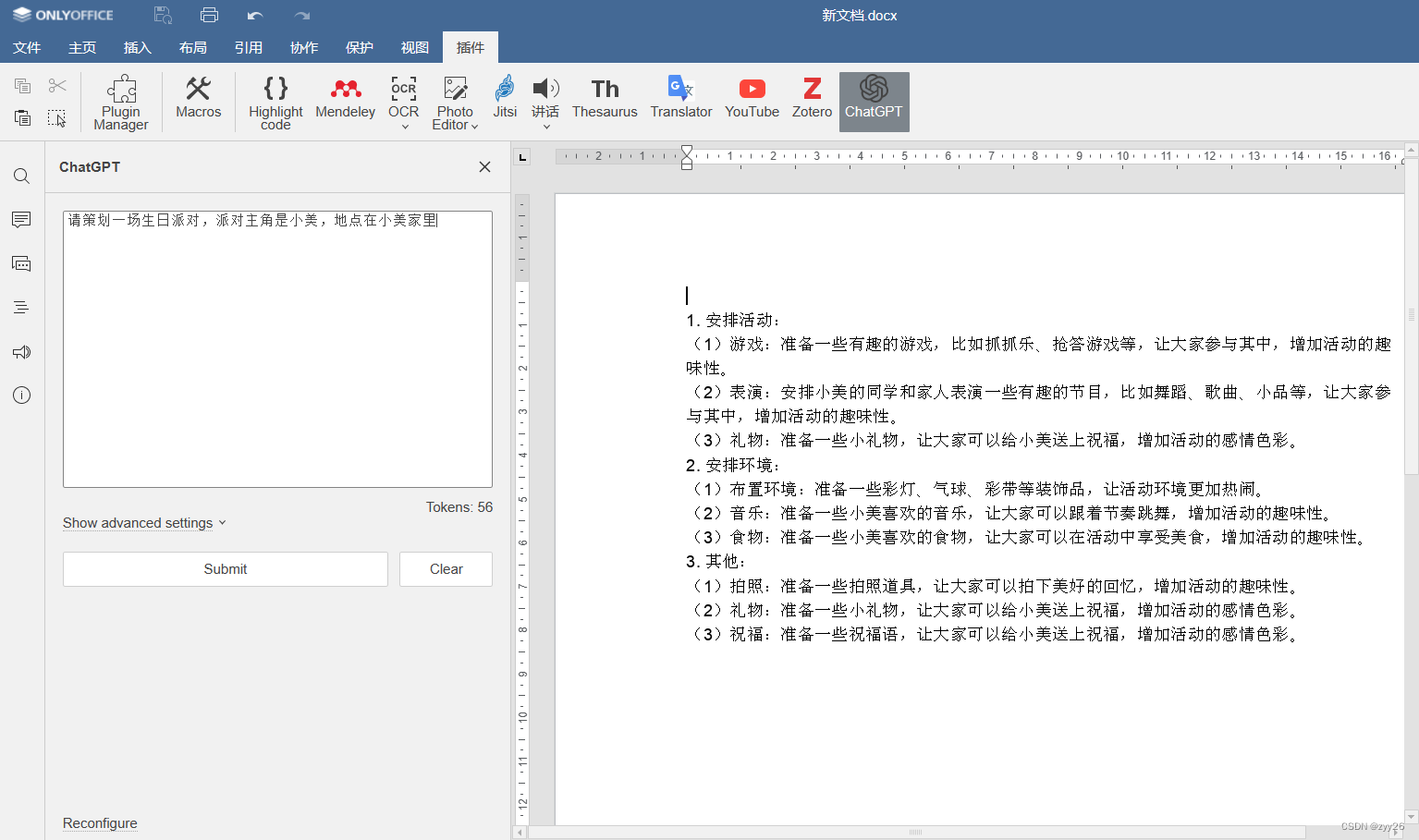
ONLYOFFICE中利用chatGPT帮助我们策划一场生日派对
近日,人工智能chatGPT聊天机器人爆火,在去年年底发布后,仅仅两个月就吸引了全球近一亿的用户,成为史上最快的应用消费程序,chatGPT拥有强大的学习和交互能力 可以被学生,教师,上班族各种职业运…...
)
Java面试题-线程(一)
在典型的 Java 面试中, 面试官会从线程的基本概念问起, 如:为什么你需要使用线程,如何创建线程,用什么方式创建线程比较好(比如:继承 thread 类还是调用 Runnable 接口),…...

一篇普通的bug日志——bug的尽头是next吗?
文章目录[bug 1] TypeError: method object is not subscriptable[bug 2] TypeError: unsupported format string passed to numpy.ndarray.__format__[bug 3] ValueError:Hint: Expected dtype() paddle::experimental::CppTypeToDataType<T>::Type()[bug 4] CondaSSLE…...

Vue 3 第八章:Watch侦听器
文章目录Watch侦听器1. 基础概念1.1. Watch的基本用法例子1:监听单个ref的值,直接监听例子2:监听多个ref的值,采用数组形式例子3:深度监听例子4:监听reactive响应式对象单一属性,采用回调函数的…...
GlassFish的安装与使用
一、产品下载与安装glassfish下载地址:https://download.oracle.com/glassfish/5.0.1/release/index.html下载后解压即完成安装,主要目录说明:bin目录:为asadmin命令所在目录。glassfish为主目录:glassfish\bin目录为命…...
【java】Java 重写(Override)与重载(Overload)
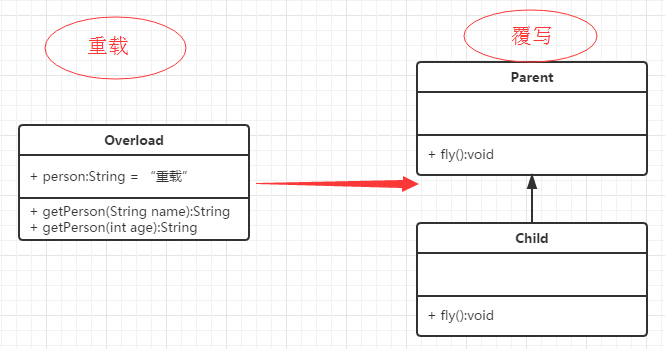
文章目录重写(Override)方法的重写规则Super 关键字的使用重载(Overload)重载规则实例重写与重载之间的区别总结重写(Override) 重写是子类对父类的允许访问的方法的实现过程进行重新编写, 返回值和形参都不能改变。即外壳不变,核心重写! 重写的好处在于…...
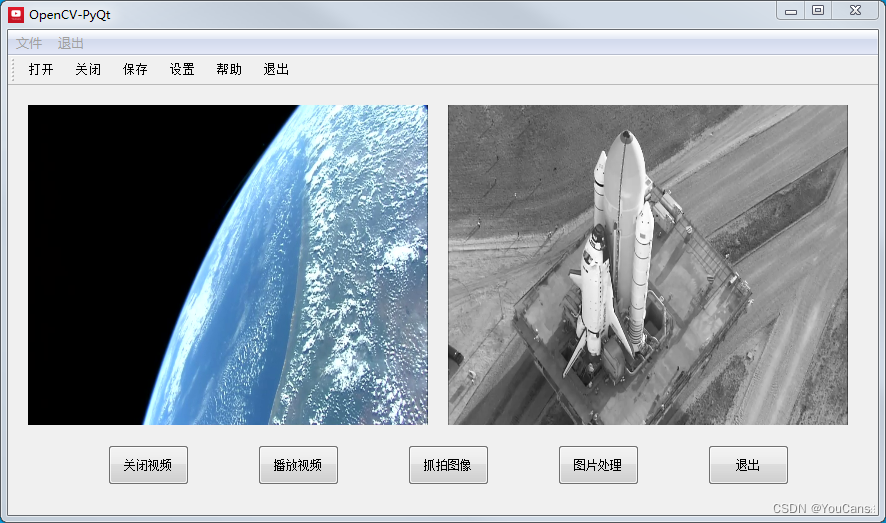
OpenCV-PyQT项目实战(12)项目案例08:多线程视频播放
欢迎关注『OpenCV-PyQT项目实战 Youcans』系列,持续更新中 OpenCV-PyQT项目实战(1)安装与环境配置 OpenCV-PyQT项目实战(2)QtDesigner 和 PyUIC 快速入门 OpenCV-PyQT项目实战(3)信号与槽机制 …...
面向对象设计模式:结构型模式之装饰器模式
文章目录一、引入二、装饰器模式2.1 Intent 意图2.2 Applicability 适用性2.3 类图2.4 优缺点2.5 应用实例:Java IO 类2.6 应用实例:咖啡馆订购系统一、引入 咖啡馆订购系统 Initial 初始 4 种咖啡 House blend (混合咖啡)Dark Roast (深度烘培)Decaf (…...
Unity iOS 无服务器做一个排行榜 GameCenter
排行榜需求解决方案一(嗯目前只有一)UnityEngine.SocialPlatformsiOS GameCenterAppStoreConnect配置Unity 调用(如果使用GameCenter系统的面板,看到这里就可以了)坑(需要获取数据做自定义面板的看这里)iOS代码Unity 代码吐槽需求 需求:接入…...

现在招个会自动化测试的人是真难呀~你会个锤子的自动化测试
现在招个会自动化测试的人是真难呀~ 前一段时间公司计划要招2个自动化测试到岗,同事面试了十几个来应聘的人,发现一个很奇怪的现象,在面试的时候,如果问的是框架API、脚本编写这些问题,基本上所有人都能对答如流&…...

OracleDatabase——数据库表空间dmp导出与导入
由于公司的程序一直部署在客户现场内网,内网调试难度高,一般是有备份还原数据库的需求,这里简记备份(导出)数据库dmp文件与恢复(导入)的步骤。 一、导出dmp文件 exp与expdp命令异同 相同点&a…...
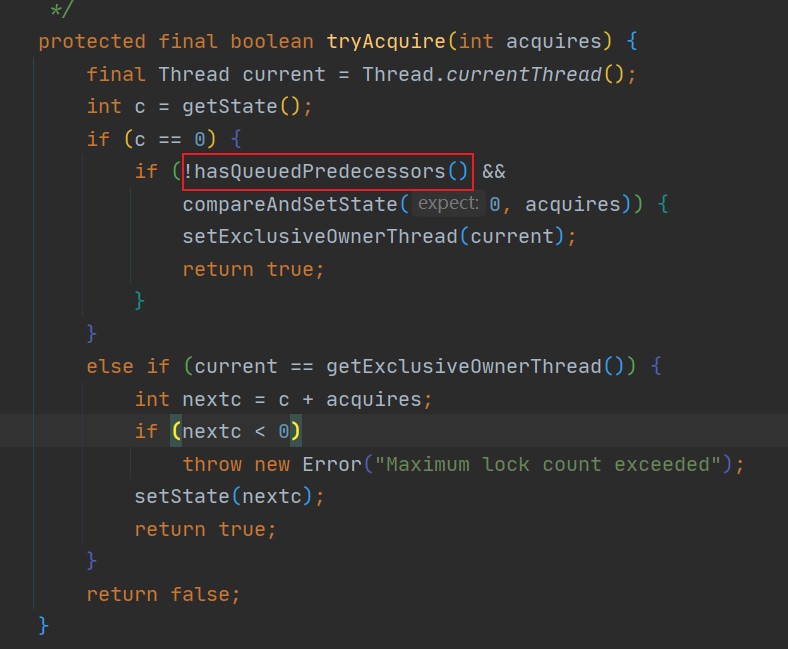
20张图带你彻底了解ReentrantLock加锁解锁的原理
哈喽大家好,我是阿Q。 最近是上班忙项目,下班带娃,忙的不可开交,连摸鱼的时间都没有了。今天趁假期用图解的方式从源码角度给大家说一下ReentrantLock加锁解锁的全过程。系好安全带,发车了。 简单使用 在聊它的源码…...

Dockerfile构建Springboot镜像
Dockerfile构建Springboot镜像 文章目录 Dockerfile构建Springboot镜像 简介实例演示 前期准备 Docker环境Springboot项目Dockerfile文件 Windows 要求构建镜像启动测试 Linux 要求构建镜像启动测试 简介 容器技术大流行的时代,也是docker大流行的时代。 此文…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
