【数据结构】06图
图
- 1. 定义
- 1.1 无向图和有向图
- 1.2 度、入度和出度
- 1.3 图的若干定义
- 1.4 几种特殊的图
- 2. 图的存储
- 2.1 邻接矩阵-顺序存储(数组)
- 2.2 邻接表-顺序存储+链式存储(数组+链表)
- 2.3 十字链表-适用于有向图
- 2.4 邻接多重表-适用于无向图
- 3. 图的基本操作
- EdgeExist(G,v,w)
- AllAdjVex(G,v)
- InsertVex(G,v)
- DeleteVex(G,v)
- InsertEdge(G,v,w)
- 4. 图的遍历
- 4.1 广度优先搜索(BFS)
- 4.2 深度优先搜索(DFS)
1. 定义
图(Graph)是一种比线性表和树更复杂的数据结构。在线性表中,数据元素之间是一对一的关系,每个数据元素只有一个直接前驱和一个直接后继。在树形结构中,数据元素之间有明显的层次关系,上一层的数据元素(结点)和下一层的数据元素(结点)是一对多的关系。而在图形结构中,数据元素之间的关系是任意的,是多对多的关系。
在图中,数据元素通常称作顶点(Vertex),简称V,是有穷非空的集合,记为 V = { v 1 , v 2 , . . . v n } V=\{v_1,v_2,...v_n\} V={v1,v2,...vn},|V|表示顶点个数。两个顶点之间的关系称作边(Edge),简称E,是有穷的集合,记为 E = ( u , v ) ∣ u ∈ V , v ∈ V E={(u,v)|u\in{V},v\in{V}} E=(u,v)∣u∈V,v∈V,|E|表示边的条数。
图简称G,由顶点集V和边集E组成,记作G=(V,E)

第三幅图不是图的数据结构
1.1 无向图和有向图

图G1中,每条边是没有方向的(无向边),则图G1是无向图。
图中的边是顶点的无序对,例如顶点V1和V2之间的边,记作(V1,V2)或(V2,V1)都可以。
G1=(V1,E1)
V1={V1,V2,V3,V4,V5}
E1={(V1,V2),(V1,V3),(V2,V4),(V3,V5)}

图G2中,每一条边是有方向的(有向边),则图G2是有向图
图中的边是顶点的有序对,例如顶点V2和V1之间的边只能记作<V2,V1>
G2={V2,E2}
V2={V1,V2,V3,V4,V5}
E2={<V2,V1>,<V1,V3>,<V3,V5>,<V5,V3>}
有向边也称为弧,<V2,V1>称为顶点V2到顶点V1的弧。V2是弧尾(初始点),V1是弧头(终端点)。顶点V2邻接到顶点V1。
简单图:不存在重复的边,不存在顶点到自身的边
1.2 度、入度和出度
无向图:
- 顶点的度:与该顶点关联的边的条数。图G1中,TD(V1)=2,TD(V2)=2…
- 无向图中全部顶点的度的和=边数X2
有向图:
- 入度:以该顶点为终点的边的条数:ID(V1) = 1,TD(V2)=0
- 出度:以该顶点为起点的边的条数:OD(V1)=1,OD(V2)=1
- 度:顶点的度是该顶点的入度和出度之和,TD(V1)=ID(V1)+OD(V1)=2
- 有向图中全部顶点的入度之和等于出度之和
1.3 图的若干定义
路径:从顶点Vx到Vy的顶点序列
回路:第一个顶点和最有一个顶点相同的路径成为回路或环
简单路径:在路径的序列中,顶点没有重复出现
简单回路:除第一个顶点和最后一个顶点外,其他顶点没有重复出现
路径长度:路径上边的条数
顶点到顶点的距离:顶点之间最短路径的长度,如果不存在路径,记为无穷 ∞ \infin ∞
在无向图中,如果顶点Vx到顶点Vy有路径,表示Vx和Vy是连通的。
在有向图中,如果顶点Vx到顶点Vy和顶点Vy到顶点Vx都有路径,表示Vx和Vy是强连通的。
连通图:任意两个顶点都是连通的。
强连通图:任意两个顶点都是强连通的。
生成子图:生成子图包含了原图的全部顶点和若干条边
连通分量:无向图中,极大的连通子图称之为连通分量(是连通子图 每个连通子图尽可能包含更多的顶点和边)
强连通分量:有向图中,极大的强连通子图称之为强连通分量(是强连通子图 每个强连通子图金肯包含更多的顶点和边)
生成树:无向连通图中,生成树是指包含了全部顶点的极小连通子图(连通图 全部顶点 边最少)
带权图:在一个图中,边可以表示某种含义的数值,例如顶点之间的距离,该数值称为边的权值。如果图的边上带了权值,那么该图称为带权图,或网。带权图中,某条路径上全部边的权值之和,称为该路径的带权路径长度。
1.4 几种特殊的图
- 完全图
- 无向完全图:图中任意两个顶点都存在一条边
- 有向完全图:图中任意两个顶点都存在方向相反的两条边
- 稀疏图和稠密图:边很少的图称为稀疏图,反之称为稠密图
- 树:不存在回路的连通无向图
- 有向树:有且仅有一个结点的入度为0,除树根外的结点入度为1,从树根到任一结点有一条有向通路
2. 图的存储
图的存储方式有四种:邻接矩阵、邻接表、十字链表、邻接多重表
2.1 邻接矩阵-顺序存储(数组)
图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一维数组存储顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。


- 对于图:结点之间有连接则边表中对应项记为1,无连接则记为0。但是无向图是A-C和C-A都有,然而有向图则只有C-A没有A-C,需要看清方向。
- 在无向图的邻接矩阵中,顶点的度为该顶点所在行或列中非零元素的个数。
- 在有向图的邻接矩阵中,顶点的出度为该顶点所在行中的非零元素的个数,入度为该顶点所在列中的非零元素个数。顶点的度=出度+入度
对于A顶点:无向图的度=3,有向图的度=1+2=3 - 对于带权图,把每条边的权值存入邻接矩阵,如果顶点之间不存在边存入无穷表示
// 利用邻接矩阵存储图
typedef char VertType; // 定义顶点的数据类型
typedef int EdgeType; // 定义边权的数据类型
#define MAXVNUM 100 // 顶点的最大数值
#define INFINITY 65536 // 无穷常量,也可以用边的权值不可能出现的值struct MGraph
{VertType vexs[MAXVNUM]; // 顶点表EdgeType edges[MAXVNUM][MAXVNUM]; // 带权边表,邻接矩阵int vexnum, arcnum; // 顶点数|V|和边数|E|
};
2.2 邻接表-顺序存储+链式存储(数组+链表)
顶点的信息存放在一维数组中,每个顶点的边的信息存放在边链表中。

// 边链表结构体
struct ENode
{int adjvex; // 邻接点域,存储该顶点对应的下标EdgeType info; // 存储权值ENode* next; // 指针域,指向下一个邻接顶点
};
// 顶点结构体
struct VNode
{VertType data; // 数据域,存储顶点信息ENode* first; // 边表头指针
};
// 图的结构体
struct AdjListGraph
{VNode vexs[MAXVNUM]; //顶点数组int vexnum,arcnum; // 顶点数和边数
};
2.3 十字链表-适用于有向图
十字链表就是有两个边链表的邻接表。

2.4 邻接多重表-适用于无向图
1)边链表结点有冗余,无向图中对于A-B之间的边,在A的边链表中有B,在B的边链表中有A,只需要一个就能表达含义了。
2)删除边和顶点操作很麻烦,时间复杂度高。

3. 图的基本操作
EdgeExist(G,v,w)
判断图G中是否存在从顶点v到顶点w的边,(v,w)或<v,w>,如(G,C,D)。
- 邻接矩阵:检查C行D列是否为1。
- 邻接表中:检查C顶点的边链表中是否有顶点D。
AllAdjVex(G,v)
列出图G中与顶点v邻接的边,如(G,C)
对于无向图:
- 邻接矩阵:检查C整(行)列,输出为1对应的顶点
- 邻接表:检查顶点C的边链表,输出顶点。
对于有向图:邻接的边包括出边和入边
- 邻接矩阵:检查C整行,输出为1对应的顶点(出边);检查C整列,输出为1对应的顶点(入边)。
- 邻接表:访问顶点C对应的边链表,输出顶点(出边);依次访问每个顶点(除C自身)的边链表,如果有C,则输出该顶点(入边)。
InsertVex(G,v)
在图G中插入顶点v,此时不需要插入边,只用插入顶点。
DeleteVex(G,v)
从图G中删除顶点v,如(G,C)。删除顶点C。(真删除和伪删除)
对于无向图:
- 邻接矩阵:删除顶点表中的C,后续元素前移;邻接矩阵中删除C对应的行列,并移动元素
- 邻接表:删除顶点表中的C,以及对应的边链表。还要遍历其他顶点,删除边链表中的C
InsertEdge(G,v,w)
在图G中插入一条从顶点v到w的边。如(G,C,D)
无向图
- 邻接矩阵:C行D列和D行C列都需要置为1
- 邻接表:顶点C的边链表中插入新结点D;顶点D的边链表中插入新结点C。
有向图: - 邻接矩阵:C行D列置为1
- 邻接表:顶点C的边链表中插入新结点D
4. 图的遍历
4.1 广度优先搜索(BFS)
图的广度优先搜索类似于树的层次遍历,需要使用一个辅助队列和辅助数组(用于记录已经访问过的数组)来实现

图的遍历可以从任意一个结点开始,假设从顶点2开始。顶点2入队,并查找visited数组中对应的下标是否已经访问,没有置为true。

出队队头元素,并将其邻接点未访问顶点入队,包括5,6,3,1

出队队头元素,并将其邻接点未访问顶点入,5出队后没有入队,6出队后入队7
 出队队头元素,并将其邻接点未访问顶点入,3出队后没有元素入队,1出队后入队4
出队队头元素,并将其邻接点未访问顶点入,3出队后没有元素入队,1出队后入队4

出队队头元素,并将其邻接点未访问顶点入,7出队后没有元素入队,4出队后入队8,9

出队队头元素,8,9。队列为空,遍历完成。
4.2 深度优先搜索(DFS)
图的深度优先搜索与图的先序遍历类似。可以利用递归或者栈的形式实现。具体就不在这里展开了。
相关文章:

【数据结构】06图
图 1. 定义1.1 无向图和有向图1.2 度、入度和出度1.3 图的若干定义1.4 几种特殊的图 2. 图的存储2.1 邻接矩阵-顺序存储(数组)2.2 邻接表-顺序存储链式存储(数组链表)2.3 十字链表-适用于有向图2.4 邻接多重表-适用于无向图 3. 图…...

Flink作业 taskmanager.numberOfTaskSlots 这个参数有哪几种设置方式
Flink作业 taskmanager.numberOfTaskSlots 这个参数有哪几种设置方式 taskmanager.numberOfTaskSlots 参数用于设置每个TaskManager上的任务槽(task slot)数量,决定了TaskManager可以并行执行的任务数量。这个参数可以通过多种方式进行设置。…...
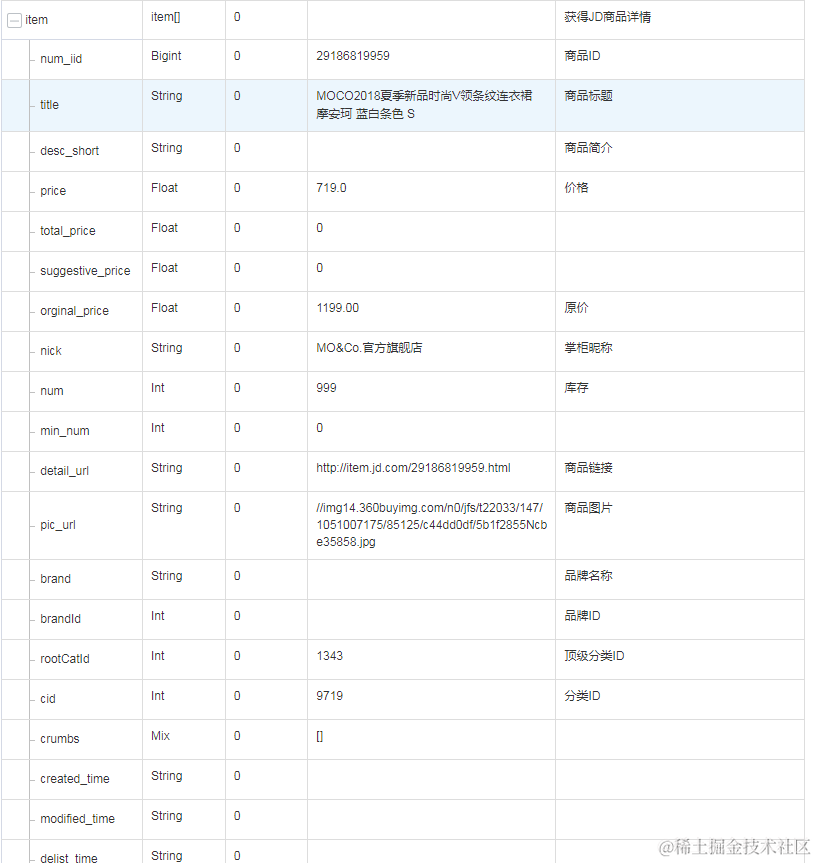
京东详情比价接口优惠券(2)
京东详情API接口在电子商务中的应用与作用性体现在多个方面,对于电商平台、商家以及用户都带来了显著的价值。 首先,从应用的角度来看,京东详情API接口为开发者提供了一整套丰富的功能和工具,使他们能够轻松地与京东平台进行交互。…...

Python knn算法
KNN(K-Nearest Neighbors)算法,即K最近邻算法,是一种基本且广泛使用的分类和回归方法。在分类问题中,KNN通过查找一个样本点的K个最近邻居,然后根据这些邻居的类别通过多数投票或加权投票来预测该样本点的类…...
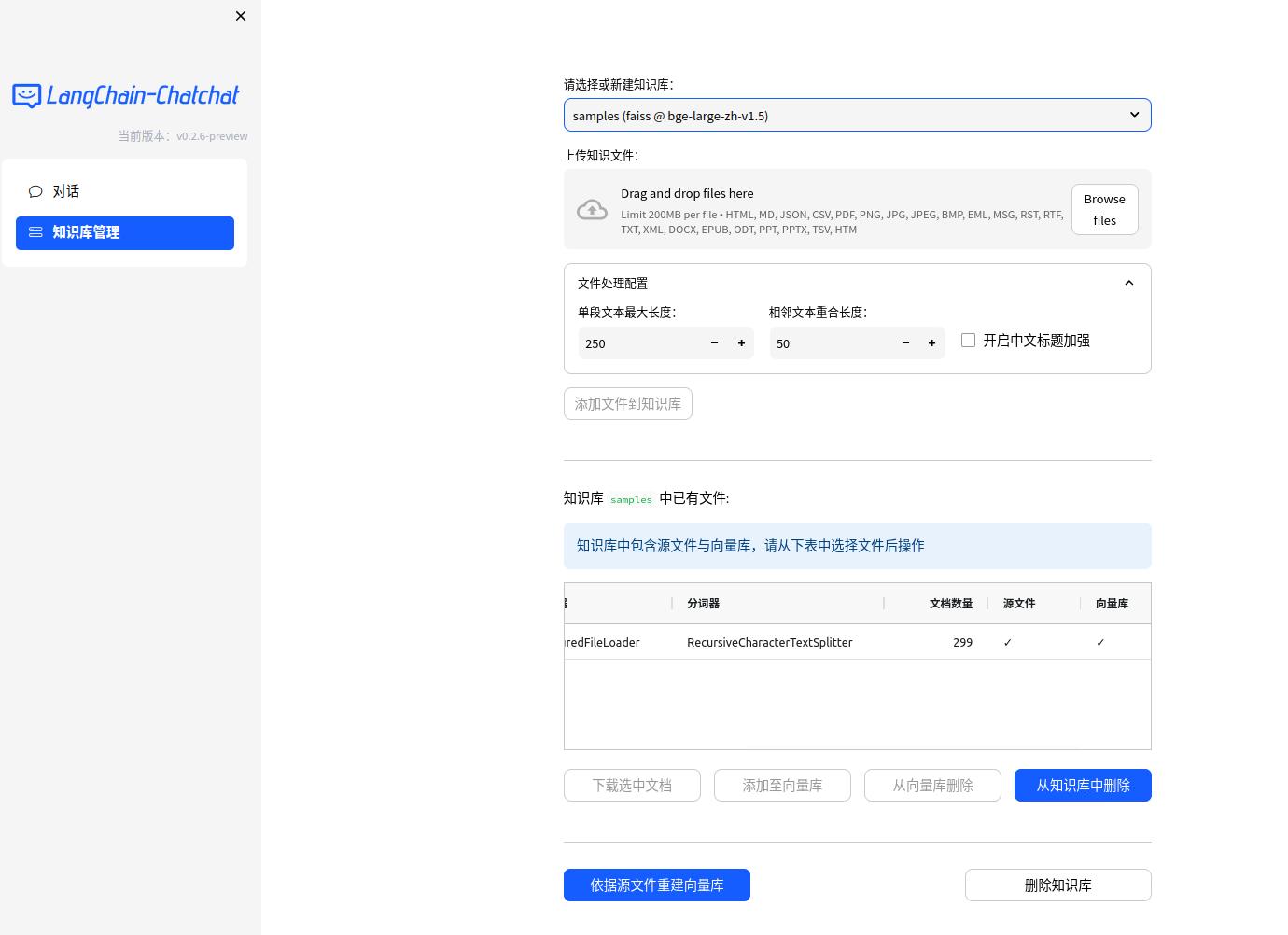
[大模型]Langchain-Chatchat安装和使用
项目地址: https://github.com/chatchat-space/Langchain-Chatchat 快速上手 1. 环境配置 首先,确保你的机器安装了 Python 3.8 - 3.11 (我们强烈推荐使用 Python3.11)。 $ python --version Python 3.11.7接着,创建一个虚拟环境ÿ…...

K8S之资源管理
关于资源管理,我们会从计算机资源管理(Computer Resources)、服务质量管理(Qos)、资源配额管理(LimitRange、ResourceQuota)等方面来进行说明 Kubernetes集群里的节点提供的资源主要是计算机资源…...

Grok-1.5 Vision:X AI发布突破性的多模态AI模型,超越GPT 4V
在人工智能领域,多模态模型的发展一直是科技巨头们竞争的焦点。 近日,马斯克旗下的X AI公司发布了其最新的多模态模型——Grok-1.5 Vision(简称Grok-1.5V),这一模型在处理文本和视觉信息方面展现出了卓越的能力&#x…...
【御控物联】Java JSON结构转换(1):对象To对象——键值互换
文章目录 一、JSON是什么?二、JSON结构转换是什么?三、核心构件之转换映射四、案例之《JSON对象 To JSON对象》五、代码实现六、在线转换工具七、技术资料 一、JSON是什么? Json(JavaScript Object Notation)产生于20…...
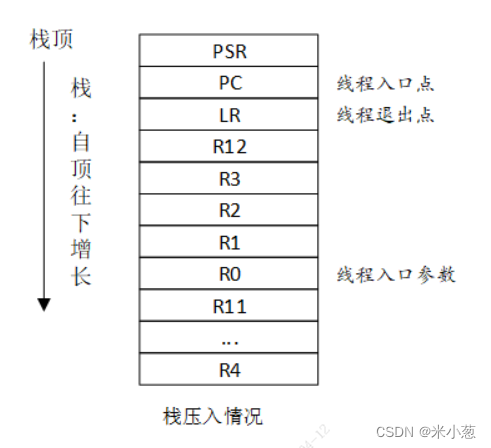
【学习笔记】rt-thread
任务 创建好任务,不管是动态还是静态创建,任务的状态是init ,通过start方法来启动任务;线程大小 设置小了,无法正常工作?显示占空间100% 启动过程 TODO 这是编译器特性? 因为RT-Thread使用编…...

一文掌握 React 开发中的 JavaScript 基础知识
前端开发中JavaScript是基石。在 React 开发中掌握掌握基础的 JavaScript 方法将有助于编写出更加高效、可维护的 React 应用程序。 在 React 开发中使用 ES6 语法可以带来更简洁、可读性更强、功能更丰富,以及更好性能和社区支持等诸多好处。这有助于提高开发效率,并构建出更…...
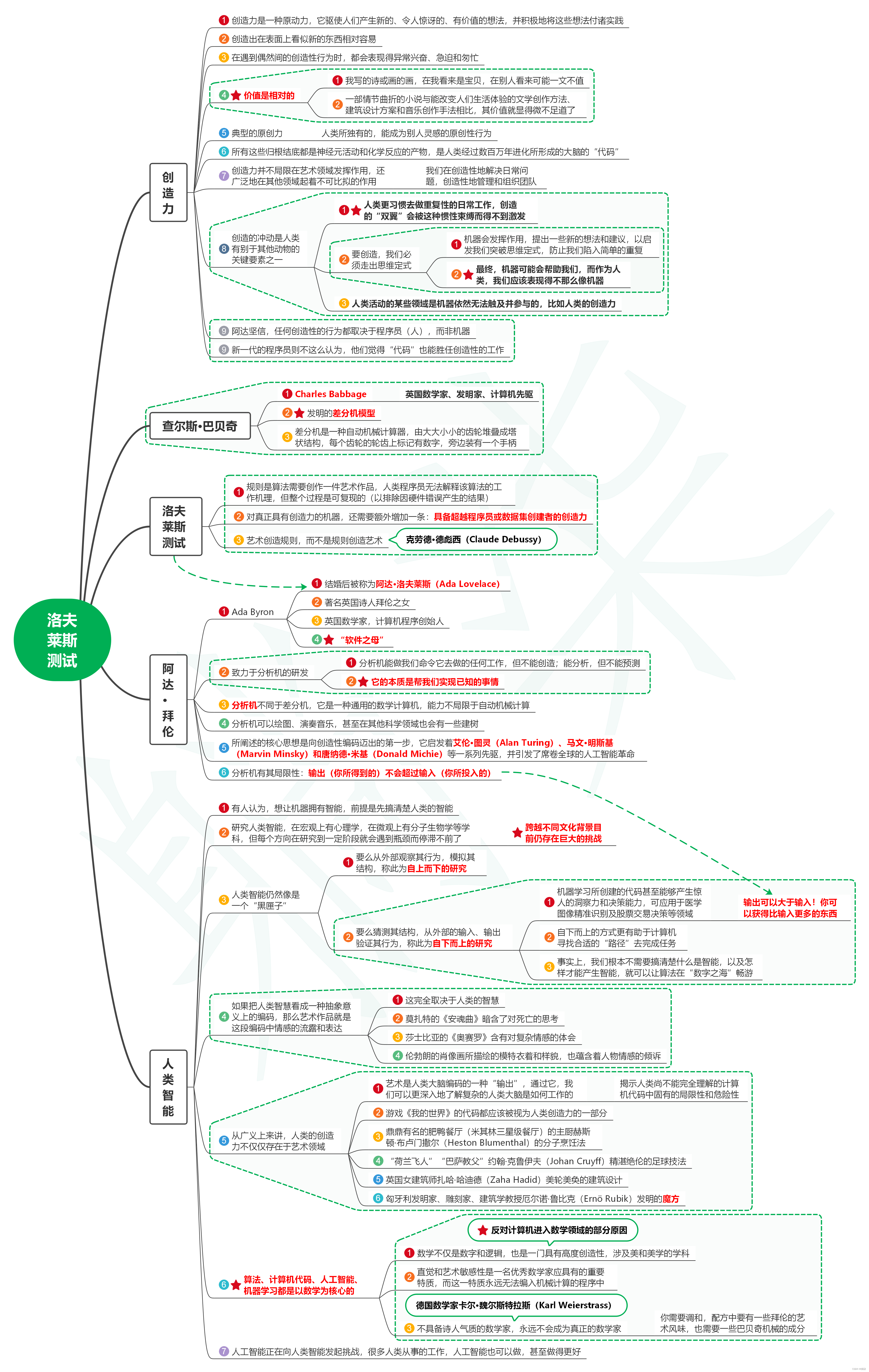
读天才与算法:人脑与AI的数学思维笔记01_洛夫莱斯测试
1. 创造力 1.1. 创造力是一种原动力,它驱使人们产生新的、令人惊讶的、有价值的想法,并积极地将这些想法付诸实践 1.2. 创造出在表面上看似新的东西相对容易 1.3. 在遇到偶然间的创造性行为时,都会表现得异…...

嵌入式系统的时间保存问题,hwclock保存注意事项
几个要点 嵌入式板子要有RTC电路和钮扣电池。这个跟电脑主板一样。嵌入式系统要有相应的驱动。使用date设置时间 date -s "2024-04-11 10:33:26" 使用hwclock保存时间 嵌入式系统如何使用hwclock正确保存时间-CSDN博客...

jenkins(docker)安装及应用
jenkins Jenkins是一个开源的、提供友好操作界面的持续集成(CI)工具,起源于Hudson(Hudson是商用的),主要用于持续、自动的构建/测试软件项目、监控外部任务的运行(这个比较抽象,暂且写上,不做解…...

uni-app中,页面跳转前,进行拦截处理的方法
个人需求阐述: 当用户在页面A中,填写了内容之后,没有点击“保存/确定”,直接通过点击返回按钮或者手机的物理返回键直接返回时,需要给出一个二次确认的弹层,当用户点击确定离开之后,跳转到页面B…...

Jmeter参数化的 4 种方式用法总结
参数化就是用变量代替数据的过程,总结参数化的4种方式: 1、用户自定义变量 用户自定义变更有两种方法: (1)在测试计划面板中的用户定义的变量设置 说明:在此用户定义的变量对所有测试计划都会生效 &…...

华为OD机试 - 连续天数的最高利润额(Java 2024 C卷 100分)
华为OD机试 2024C卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试(JAVA)真题(A卷B卷C卷)》。 刷的越多,抽中的概率越大,每一题都有详细的答题思路、详细的代码注释、样例测试…...

C语言——内存函数的实现和模拟实现
1. memcpy 使用和模拟实现 void * memcpy ( void * destination, const void * source, size_t num ); 函数memcpy从source的位置开始向后复制num个字节的数据到destination指向的内存位置。 这个函数在遇到 \0 的时候并不会停下来。 如果source和destination有任何的重叠&am…...

如何优化邮箱Webhook API发送邮件的性能?
邮箱Webhook API发送邮件的流程?怎么用邮箱API发信? 高效、稳定的邮箱Webhook API发送邮件功能对于企业的日常运营至关重要。随着业务量的增长,如何优化邮箱Webhook API发送邮件的性能。AokSend将从多个方面探讨如何提升的效率。 邮箱Webho…...
)
OceanBase V4.X中常用的SQL(一)
整理了一些在OceanBase使用过程中常用的SQL语句,这些语句均适用于4.x版本,并将持续进行更新。后续还将分享一些V4.x版本常用的操作指南,以便更好地帮助大家使用OceanBase数据库。 集群信息 版本查看 show variables like version_comment; …...

代码随想录算法训练营第五十天|123.买卖股票的最佳时机III 188.买卖股票的最佳时机IV
123.买卖股票的最佳时机III 这道题一下子就难度上来了,关键在于至多买卖两次,这意味着可以买卖一次,可以买卖两次,也可以不买卖。 视频讲解:https://www.bilibili.com/video/BV1WG411K7AR https://programmercarl.com…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
